Проблематика при прогнозировании фильтрационно-емкостных параметров, включающих в себя характеристики нефтегазоносности, на сегодняшний день является важной и научно значимой, так как основана на эффективности и достоверности подсчетных параметров углеводородного сырья месторождений на разных стадиях их исследования. Однако зачастую исследуемые параметры неоднозначно определены в модели среды. На практике геолого-геофизические данные представлены нерегулярностью наблюдений исследований, для них характерны негустая сеть, разброс по вертикали и горизонтали, что в свою очередь влияет на уменьшение плотности данных. Принятие для разных интервалов одного правила, например регрессионной модели, приводит к появлению неконтролируемых ошибок. Альтернативным методом моделирования является композиция Мамдани в моделях нечеткого анализа [1].
Если задано несколько (например, два) универсумов, или переменных 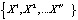 , на которых определены нечеткие величины
, на которых определены нечеткие величины 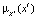 , то между ними может быть установлена связь, которая определена новой функцией принадлежности, содержащей все либо часть нечетких переменных
, то между ними может быть установлена связь, которая определена новой функцией принадлежности, содержащей все либо часть нечетких переменных 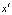 :
: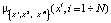 . Эта функция принадлежности определяет отношение между нечеткими величинами
. Эта функция принадлежности определяет отношение между нечеткими величинами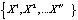 . В качестве примера такого нечёткого отношения может служить отношение, устанавливаемое результатами наблюдений [2], например, между параметрами пористости и проницаемости горных пород в пределах однородно слагающих пластов-коллекторов. Методом построения нечетких отношений могут служить введенные выше операции объединения, пересечения, дополнения нечетких множеств, выраженные через функции принадлежности:
. В качестве примера такого нечёткого отношения может служить отношение, устанавливаемое результатами наблюдений [2], например, между параметрами пористости и проницаемости горных пород в пределах однородно слагающих пластов-коллекторов. Методом построения нечетких отношений могут служить введенные выше операции объединения, пересечения, дополнения нечетких множеств, выраженные через функции принадлежности:
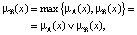
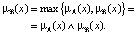 (1)
(1)
Введенные алгебраические операции также служат примером отношений между двумя нечеткими величинами (бинарные отношения). Это нечеткие отношения между двумя нечеткими величинами, формирующими третью нечеткую величину. Понятие отношения между нечеткими величинами реализует понятие связи между переменными на нечеткий случай.
Нечеткие отношения между нечеткими величинами, определенными функциями принадлежности 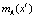 и
и 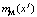 , определяют нечеткую величину
, определяют нечеткую величину 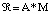 , образованную переменными
, образованную переменными 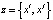 с функцией принадлежности
с функцией принадлежности 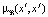 . При нечетком моделировании допустимы введенные выше операции:
. При нечетком моделировании допустимы введенные выше операции:
пересечения:
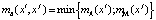 , (2)
, (2)
объединения:
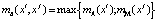 , (3)
, (3)
разности:
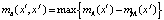 . (4)
. (4)
Помимо логических операций, над отношениями, определенными на одном и том же универсуме, могут быть введены операции композиции между двумя бинарными (содержащими два параметра) отношениями μA(x, y) и μM(y, z), а также операция между бинарным отношением μA(x, y) и функцией принадлежности нечеткой величины μM(x). Эти композиции играют особо значимую роль в последующих построениях.
Материалы и методы исследования
Важной задачей в развиваемых далее методах прогноза фильтрационно-емкостных параметров, основанных на нечеткой математике, является расчёт функции принадлежности для нечётких отношений. Иными словами, по известному и доверительному отношению двух нечетких величин с использованием функции принадлежности выполняется анализ достоверности, позволяющий в дальнейшем построить дефазификацию имеющейся связи и поискового параметра. Рассмотрим математическую модель со следующими переменными: имеются нечёткие отношения μA(x, y) для переменных (x, y) и определена функция принадлежности μM(x). Следует дать оценку для функции принадлежности μA*M(y). Здесь, символом A обозначена нечеткая переменных двух аргументов – (x, y), образующих нечеткое отношение μA(x, y); символом M – нечеткая переменная x; A*M – символ композиции нечетких переменных A и M, определяющий независимую переменную y, полученный по итогам расчета. Процедура такого вычисления μA*M(y) называется композицией нечеткого отношения и нечеткой величины. В литературе подобный подход встречается под термином «правило нечеткого логического вывода». В практике данный подход рассматривается как расчет значений переменной y, по известной связи между x и y, и заданной нечеткой переменной x.
Для реализации метода нечеткого логического вывода используются следующие операции:
Правило нечеткого логического вывода Мамдани [3]:
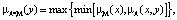
или
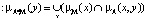 . (5)
. (5)
Операция Max-prod композиция:
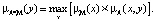
Операция Min-max композиция:
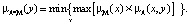
Операция Max-max композиция:
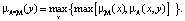
Операция Min-min композиция:
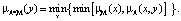
Операция Min-average композиция:
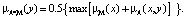
Полезной является следующая аналогия.
Если μA(x, y) рассматривать как матрицу A, со значениями 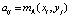 , где (xi, yj) – значения переменных в узлах Mi N сетки, а вектор
, где (xi, yj) – значения переменных в узлах Mi N сетки, а вектор 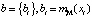 , то соотношением Ab определен вектор
, то соотношением Ab определен вектор 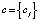 . По правилам линейной алгебры:
. По правилам линейной алгебры: 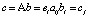 будет в точности определять μA*M(yj), если операцию умножения воспринимать как логическое умножение:
будет в точности определять μA*M(yj), если операцию умножения воспринимать как логическое умножение: 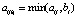 , а сложение – как логическое объединение:
, а сложение – как логическое объединение: 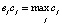 .
.
Таким образом, операция (5) соответствует обычным алгебраическим правилам умножения матрицы на вектор, с заменой алгебраических операций на их логические аналоги.
При моделировании особое внимание уделяется построенной композиции между двумя нечеткими отношениями μA(x, y) и μM(x, y). Процедура вычисления выполняется подстановкой в четкое уравнение переменных (x,y) и уравнения между другой парой переменных (y,z). Целевой задачей является исключение из результата переменной y и получение уравнения связи между (x, z) [4]. Выполнение данной выполняется с помощью формулы Мамдани:
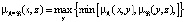 . (6)
. (6)
По приведенной выше аналогии с матрицами расчет по формуле (6) в точности соответствует умножению матриц  ;
; 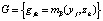 с заменой алгебраических операций умножения и сложения на логические – пересечения и объединения, тождественные вычислению минимума и максимума.
с заменой алгебраических операций умножения и сложения на логические – пересечения и объединения, тождественные вычислению минимума и максимума.
Предположим, что следует установить отношение между переменными (x, z) по известному отношению μA(x, y) и 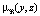 . Определим переменные: x – коэффициент пористости, выполненный по данным ГИС; z – коэффициент проницаемости. Кроме этого, определена связь μA(x, y) между x и промежуточным параметром y и
. Определим переменные: x – коэффициент пористости, выполненный по данным ГИС; z – коэффициент проницаемости. Кроме этого, определена связь μA(x, y) между x и промежуточным параметром y и 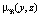 , характеризующая отношение между y и z.
, характеризующая отношение между y и z.
Определим следующий алгоритм расчета функции принадлежности для отношений: по исходной функции принадлежности μM(x) и μA(x, y) рассчитаем
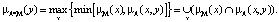 (7)
(7)
По вычисленной μA*M(y) и заданному отношению 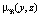 получаем
получаем
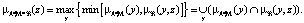 (8)
(8)
Подставляя (7) для μA*M(y) в (8), получаем
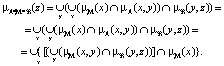 (9)
(9)
Определив
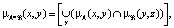 (10)
(10)
получаем для 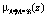 :
:
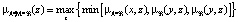 . (11)
. (11)
Проведенные исследования тождественно отображают (5), в результате чего можно сделать вывод, что композиция Мамдани (10) отношений μA(x, y) и 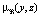 имеет смысл аналогичный подстановке уравнений для исключения общих повторяющихся переменных.
имеет смысл аналогичный подстановке уравнений для исключения общих повторяющихся переменных.
Результаты исследования и их обсуждение
Представленные математические аспекты использования правил нечеткой математики для нечеткого моделирования в нефтегазовой геологии и анализа неопределенных нечетких данных результатов экспериментов играют значимую роль при обработке и интерпретации сложнопостроенных сред, с целью оценки достоверности построения прогнозных задач. Приведем типичные примеры работы операции композиции Мамдани.
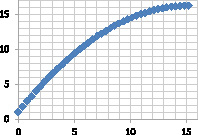
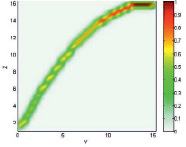
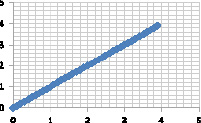
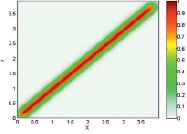
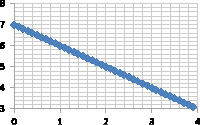
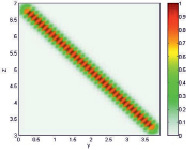
На рис. 1 и 2 приведены исходные данные и их нечеткие модели для отношений μA(x, y) и 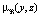 .
.
|
а) Исходные данные |
Нечеткая модель |
|
|
|
|
б) Исходные данные |
Нечеткая модель |
|
|
|
|
в)
|
|
Рис. 1. Демонстрация нечеткого моделирования для линейных зависимостей: а) модель для отношения μA(x, y); б) модель для отношения 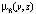 ; в) композиция Мамдани
; в) композиция Мамдани 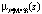 этих отношений
этих отношений
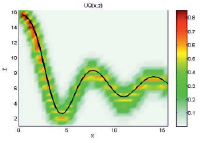
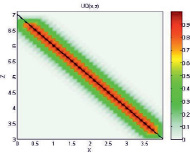
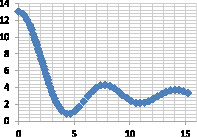
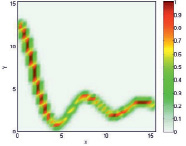
Для нелинейных зависимостей:
|
а) Исходные данные (модель) |
Нечеткая модель |
|
|
|
|
б) Исходные данные (модель |
Нечеткая модель |
|
|
|
|
в)
|
|
Рис. 2. Демонстрация нечеткого моделирования для нелинейных зависимостей: а) модель для отношения μA(x, y); б) модель для отношения 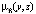 ; в) композиция Мамдани
; в) композиция Мамдани 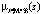 этих отношений
этих отношений
Заключение
Проведенные исследования полностью нашли свое подтверждение в справедливости использования при нечетком моделировании композиции Мамдани. Предлагаемая технология играет важную роль для установления отношений между величинами, характеризующими петрофизические и геофизические свойства горных пород в моделях нечеткого анализа. Однако при такой постановке может быть введена и альтернативная операция композиции max*:
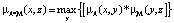 . (12)
. (12)
Роль символа «*» играет некоторая операция, например умножение.
В источнике [4] подробно продемонстрировано явное преимущество композиции Мамдани в сравнении с альтернативными способами.
Анализируя приведенные алгебраические вычисления, обозначив композицию между двумя бинарными отношениями, можно сделать вывод, что она ассоциативна, дистрибутивна относительно нечеткого объединения. При вычислении функции от каждой из переменных, входящих в нечеткое отношение, порядок композиции не имеет значения, т.е. отношение является инвариантом, что особо важно при формировании графов прогноза параметров.
Полученные композиции Мамдани применительны и к другим геофизическим параметрам, как, например, сейсмические атрибуты и петрофизические характеристики геологической среды. В результате выполнения прогноза они имеют оценку, ранжированную по достоверности, что позволит более точно решать такие задачи, как подсчет запасов углеводородов, изучение и исследование процесса вытеснения углеводородов в коллекторах, определение и контроль перемещения водонефтяного и газожидкостного контакта в пласте, а также оценки перспектив нефтегазоносности [5].
Библиографическая ссылка
Шилова С.В., Бурмистрова О.Н. КОМПОЗИЦИЯ МАМДАНИ В МОДЕЛЯХ НЕЧЕТКОГО АНАЛИЗА КАК НЕЧЕТКИЙ АНАЛОГ ПОДСТАНОВОК ЗАВИСИМОСТЕЙ // Современные наукоемкие технологии. 2021. № 10. С. 102-107;URL: https://top-technologies.ru/ru/article/view?id=38861 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/snt.38861




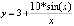
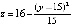 )
)