Линейная многомерная регрессия – одна из распространенных математических моделей при исследовании стохастических систем [1–3]. Для ее использования по наблюдаемым данным (X, y) оценивают вектор a коэффициентов в модели
 , (1)
, (1)
где 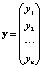 ,
, 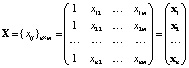 ,
, 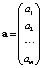 ,
, 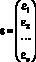 - вектор ненаблюдаемых случайных погрешностей (ошибок, невязок).
- вектор ненаблюдаемых случайных погрешностей (ошибок, невязок).
Наиболее распространенным методом оценивания параметров регрессионных моделей по экспериментальным данным является метод наименьших квадратов (МНК). Однако данный метод требует выполнения ряда предпосылок, называемых условиями Гаусса – Маркова [4, 5], и при их нарушении может приводить к значительному снижению достоверности моделирования. В этой ситуации применяют устойчивые методы, в первую очередь основанные на минимизации суммы модулей (или функций от модулей) невязок. В первом случае используется метод наименьших модулей (МНМ) [6, 7]. МНМ для нахождения коэффициентов регрессии в (1) представляет собой задачу минимизации
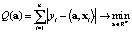 . (2)
. (2)
Для обеспечения большей устойчивости можно применять обобщенный метод наименьших модулей (ОМНМ) [8]. ОМНМ-оценки для (1) находят как решение задачи
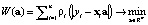 , (3)
, (3)
где r(∙) – некоторая монотонно возрастающая, дважды непрерывно-дифференцируемая на положительной полуоси функция, причем 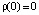 ,
, 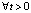
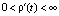 ,
, 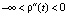 .
.
МНМ и ОМНМ объединяет общее свойство – в обоих случаях решение находится в узловых точках. В [9, 10] был предложен новый подход к решению задач (2) и (3) на основе спуска по узловым прямым. Так средняя вычислительная сложность алгоритма градиентного спуска по узловым прямым для реализации МНМ составила O(m2n1,4) [10], а вычислительная сложность нахождения ОМНМ-оценки – 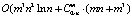 , где a – доля гиперплоскостей, ближайших к текущей узловой точке, рассматриваемых на каждой итерации [9]. Несмотря на достаточно высокое быстродействие, вычислительная эффективность данных алгоритмов может оказаться недостаточной для решения задач мониторинга состояния систем, в которых оценивание параметров модели происходит в режиме реального времени в темпе поступления новых входных данных.
, где a – доля гиперплоскостей, ближайших к текущей узловой точке, рассматриваемых на каждой итерации [9]. Несмотря на достаточно высокое быстродействие, вычислительная эффективность данных алгоритмов может оказаться недостаточной для решения задач мониторинга состояния систем, в которых оценивание параметров модели происходит в режиме реального времени в темпе поступления новых входных данных.
Цель исследования – повышение вычислительной эффективности алгоритмов спуска по узловым прямым для решения динамических задач мониторинга состояния систем. Рассмотрим обе задачи – (2) и (3).
Материалы и методы исследования
Введем гиперплоскости 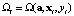 в виде уравнений
в виде уравнений
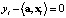 ,
, 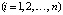 . (4)
. (4)
Зададим также узловые точки пересечения гиперплоскостей (4)
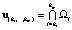 ,
,
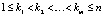 ,
, 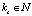 . (5)
. (5)
Будем называть узловой прямую, являющуюся пересечением (m - 1) непараллельных гиперплоскостей Wi:
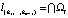 ,
, 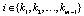 . (6)
. (6)
Обозначим: 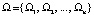 – множество всех гиперплоскостей, U – множество всех узловых точек (5). Минимум целевых функций Q(a) и W(a) всегда принадлежит множеству U.
– множество всех гиперплоскостей, U – множество всех узловых точек (5). Минимум целевых функций Q(a) и W(a) всегда принадлежит множеству U.
Алгоритм решения задачи (2) основан на спуске к точному решению, двигаясь вдоль узловых прямых (6). В [9] показано, что минимум функции Q(a) принадлежит множеству U и достигается за конечное число шагов.
За начальное приближение берем узловую точку 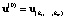 , являющуюся пересечением m произвольных гиперплоскостей
, являющуюся пересечением m произвольных гиперплоскостей 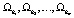 , путем решения системы линейных алгебраических уравнений (СЛАУ):
, путем решения системы линейных алгебраических уравнений (СЛАУ): 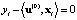 ,
, 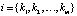 . Например, можно взять i = 1, 2, … , m. Исключив одну из гиперплоскостей, например
. Например, можно взять i = 1, 2, … , m. Исключив одну из гиперплоскостей, например 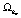 , получим узловую прямую
, получим узловую прямую 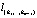 . Расширенная матрица СЛАУ прямой
. Расширенная матрица СЛАУ прямой 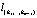 имеет вид
имеет вид
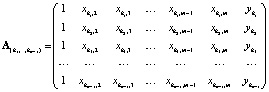 .
.
Применив алгоритм прямого хода метода Гаусса, преобразуем матрицу 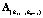 к ступенчатому виду
к ступенчатому виду
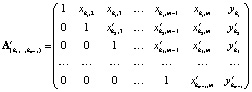 .
.
Используя ступенчатую матрицу 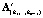 , можно значительно сократить вычислительные затраты на нахождение всех узловых точек, лежащих на прямой
, можно значительно сократить вычислительные затраты на нахождение всех узловых точек, лежащих на прямой 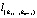 . Действительно, для любой i-й узловой точки имеем расширенную матрицу
. Действительно, для любой i-й узловой точки имеем расширенную матрицу
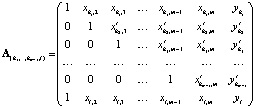 , (7)
, (7)
где 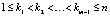 ,
, 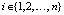 ,
, 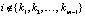 .
.
Находим все узловые точки, лежащие на 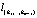 . Варьируя номер i в (7), найдем все (n - 1) узловых точек на прямой и упорядочиваем их по направлению этой прямой. Далее в алгоритмах спуска по узловым прямым в одной из узловых точек
. Варьируя номер i в (7), найдем все (n - 1) узловых точек на прямой и упорядочиваем их по направлению этой прямой. Далее в алгоритмах спуска по узловым прямым в одной из узловых точек 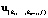 с находят помощью направленного (градиентного) спуска минимум функции Q(a) на прямой
с находят помощью направленного (градиентного) спуска минимум функции Q(a) на прямой 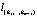 .
.
Линейный вид выражений под знаком модуля в (2) приводит к простому виду производной функции Q(a) по направлению узловой прямой. Покажем это.
В узловой точке 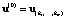 вычисляем значение производной функции Q(a) по направлению узловой прямой
вычисляем значение производной функции Q(a) по направлению узловой прямой 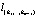 . Двигаемся из узловой точки u(0) по направлению убывания производной по направлению. Эта производная не существует только в узловых точках. Поэтому в очередной узловой точке
. Двигаемся из узловой точки u(0) по направлению убывания производной по направлению. Эта производная не существует только в узловых точках. Поэтому в очередной узловой точке 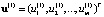 находим производную с двух сторон. Каждая из производных равна сумме n слагаемых по числу наблюдений [10]
находим производную с двух сторон. Каждая из производных равна сумме n слагаемых по числу наблюдений [10]
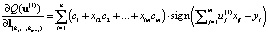 . (8)
. (8)
где 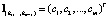 – направляющий вектор узловой прямой
– направляющий вектор узловой прямой 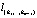 . При переходе через узловую точку изменяется только одно из слагаемых в (8). Его номер соответствует номеру гиперплоскости, пересекающей в этой узловой точке u(1) прямую
. При переходе через узловую точку изменяется только одно из слагаемых в (8). Его номер соответствует номеру гиперплоскости, пересекающей в этой узловой точке u(1) прямую 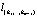 . Если знак производной по направлению перед u(1)
. Если знак производной по направлению перед u(1) 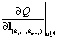 и после u(1)
и после u(1) 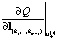 меняется с отрицательного на положительной (или производная станет равной нулю), то в этой точке целевая функция принимает наименьшее значение по узловой прямой. Тогда вместо u(0) фиксируем u(1). Если на данной прямо целевая функция в исходной узловой точке u(0) принимает наименьшее значение (производная по направлению при переходе через u(0) в ту и другую сторону становится больше или равной нулю), то переходим к следующей узловой прямой, проходящей через эту узловую точку.
меняется с отрицательного на положительной (или производная станет равной нулю), то в этой точке целевая функция принимает наименьшее значение по узловой прямой. Тогда вместо u(0) фиксируем u(1). Если на данной прямо целевая функция в исходной узловой точке u(0) принимает наименьшее значение (производная по направлению при переходе через u(0) в ту и другую сторону становится больше или равной нулю), то переходим к следующей узловой прямой, проходящей через эту узловую точку.
В случае, когда вместо u(0) фиксируем u(1), тогда из точки u(1) переходим на другую узловую прямую и продолжаем спуск по ней по тому же принципу. В результате будет найдена узловая точка u(*), спуск из которой невозможен. Эта узловая точка будет являться точным решением задачи (2). В [10] рассмотрены два варианта продолжения спуска после нахождения очередной узловой точки:
1) продолжить спуск из точки 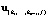 по другой узловой прямой и т.д. до тех пор, пока спуск будет невозможен;
по другой узловой прямой и т.д. до тех пор, пока спуск будет невозможен;
2) выполнить спуск из точки 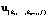 по всем остальным (m - 1) узловым прямым, найти в каждой из них минимум Q(a) и перейти в узловую точку с наименьшим значением целевой функции и снова продолжить спуск из этой точки.
по всем остальным (m - 1) узловым прямым, найти в каждой из них минимум Q(a) и перейти в узловую точку с наименьшим значением целевой функции и снова продолжить спуск из этой точки.
Однако остался открытым вопрос совмещении этих вариантов проверки узловых прямых: проведение какой-то «части» итераций с использованием одного из способов проверки узловых прямых, остальные же итерации будут производиться другим способом. Итерацией же, относительно поставленной задачи, будет считаться переход от одной узловой точки к другой.
Результаты исследования и их обсуждение
Проверим гипотезу о совмещении двух описанных ранее способов проверки узловых прямых. Данная гипотеза заключается в проведении какой-то «части» итераций с использованием одного из способов проверки узловых прямых, остальные же итерации будут производиться другим способом. Итерацией же, относительно поставленной задачи, будет считаться переход от одной узловой точки к другой.
Количество итераций, для последующего деления на «части», будет вычисляться алгоритмом при анализе выборки с использованием способа проверки узловых прямых без совмещения. К примеру, в первую очередь выборка будет проанализирована способом с полной проверкой всех прилегающих узловых прямых. Тогда в последующем, взяв количество итераций с предыдущего шага, первая «часть» итераций (в нашем случае 10 %, ..., 90 %) будет осуществлена способом с полной проверкой прямых, а все остальные – способом с переходом на первую узловую прямую с меньшим значением целевой функции.
С помощью метода статистических испытаний Монте-Карло [11, 12] было проведено исследование, в котором для m = 2, 3, ... , 10 оценивалось время решения задачи (2). Объемы выборок n = 50, 100, ..., 500. Результаты приведены в табл. 1.
Таблица 1
Доля наиболее быстрых решений задачи (2) различными способами проверки узловых прямых
|
Способ проверки прямой |
% от общего числа опытов |
Способ проверки прямой |
% от общего числа опытов |
|
First |
15,00 |
Full |
39,72 |
|
10 % |
4,44 |
10 % |
1,94 |
|
20 % |
3,89 |
20 % |
1,39 |
|
30 % |
4,72 |
30 % |
1,67 |
|
40 % |
3,33 |
40 % |
1,94 |
|
50 % |
3,06 |
50 % |
1,11 |
|
60 % |
3,61 |
60 % |
1,39 |
|
70 % |
4,17 |
70 % |
0,83 |
|
80 % |
2,78 |
80 % |
0,56 |
|
90 % |
3,61 |
90 % |
0,83 |
Примечание. Full – способ с проверкой всех прилегающих узловых прямых; First – способ с переходом на первую узловую прямую с меньшим значением целевой функции относительно исходной точки.
В итоге наилучшие результаты показал способ Full. Отметим, что подобная тенденция в скорости вычисления сохраняется как при нормальном распределении выборки, так и при наличии выбросов. Поэтому наибольшим быстродействием обладает спуск из узловой точки 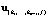 по всем m узловым прямым.
по всем m узловым прямым.
Анализ данных показал, что в этом случае среднее число рассмотренных узловых точек имеет линейную зависимость с объемом выборки n и степенную с количеством коэффициентов в наблюдении m. Среднее число рассмотренных узловых точек достаточно точно аппроксимируется зависимостью L(m, n) = O(m2n). Вычислительная сложность решения задачи (3) может быть снижена за счет более быстрого нахождения начальной точки, являющейся решением задачи (2).
Рассмотрим теперь динамическую задачу. Пусть мы нашли решение a(*) задачи (2) по начальной выборке данных (Xi, yi) = = (xi1, ... , xim, yi), i = 1, ... , n. Теперь в динамике добавляем новое наблюдение (Xn+1, yn+1), удаляем самое «старое» первое наблюдение (X1, y1) и снова оцениваем МНМ-параметры уравнения регрессии.
Решение a(*) представляет собой пересечение m гиперплоскостей (обозначим их как множество G1), образованных некоторыми m наблюдениями (обозначим их как множество Z1). Возможны два случая. Во-первых, наблюдение (X1, y1) не принадлежит к множеству Z1. Тогда считаем точку a(*) начальной точкой (присваиваем a(0) = a(*)) и начинаем искать решение по алгоритму градиентного спуска по узловым прямым.
Во-вторых, наблюдение (X1, y1) принадлежит множеству Z1. Добавляем к множеству Z1 \ (X1, y1) любое из не принадлежащих ему наблюдений, например (Xn+1, yn+1), находим пересечение оставшихся (m – 1) гиперплоскостей из множества G1 (их пересечение образует узловую прямую 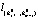 ) с гиперплоскостью Wn+1, образованной наблюдением (Xn+1, yn+1), Отметим, что гиперплоскость Wn+1 и узловая прямая
) с гиперплоскостью Wn+1, образованной наблюдением (Xn+1, yn+1), Отметим, что гиперплоскость Wn+1 и узловая прямая 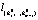 ) должны пересекаться (не должны быть параллельными). Тогда точку
) должны пересекаться (не должны быть параллельными). Тогда точку 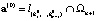 считаем начальной точкой и начинаем искать решение по алгоритму градиентного спуска по узловым прямым.
считаем начальной точкой и начинаем искать решение по алгоритму градиентного спуска по узловым прямым.
Выигрыш в быстродействии в динамике должен достигаться за счет более близкого расположения узловой точки a(0) к решению задачи (2). В [13] получено, что среднее число переходов от одной узловой прямой на другую составляет O(mlnn). Учет полученного на предыдущем шаге решения в динамической задаче должен уменьшить это число. Снова воспользуемся методом Монте-Карло. В табл. 2 для 2000 испытаний приведены средние значения p(m, n) общего количества переходов с одной узловой прямой на другую, для тех же значений m и n, что и в [13].
Таблица 2
Средние значения количества переходов с одной узловой прямой на другую
|
n |
p(m, n) |
||||
|
m = 3 |
m = 4 |
m = 5 |
m = 6 |
m = 7 |
|
|
30 |
1,64 |
2,09 |
2,49 |
2,81 |
3,02 |
|
50 |
1,66 |
2,01 |
2,44 |
2,79 |
3,11 |
|
100 |
1,70 |
2,05 |
2,44 |
2,82 |
3,18 |
|
150 |
1,63 |
2,06 |
2,44 |
2,82 |
3,26 |
|
300 |
1,65 |
2,07 |
2,40 |
2,89 |
3,19 |
|
500 |
1,62 |
2,07 |
2,53 |
2,94 |
3,28 |
|
700 |
1,65 |
2,10 |
2,51 |
2,86 |
3,33 |
|
900 |
1,58 |
2,05 |
2,46 |
2,84 |
3,23 |
|
1000 |
1,66 |
2,05 |
2,50 |
2,87 |
3,18 |
|
1200 |
1,65 |
2,09 |
2,50 |
2,82 |
3,24 |
|
1500 |
1,63 |
1,97 |
2,43 |
2,89 |
3,23 |
|
1700 |
1,67 |
2,07 |
2,46 |
2,84 |
3,25 |
|
1850 |
1,61 |
2,03 |
2,43 |
2,92 |
3,20 |
|
2000 |
1,63 |
2,08 |
2,49 |
2,81 |
3,18 |
|
Среднее P(m) |
1,64 |
2,06 |
2,47 |
2,85 |
3,21 |
Видим, что p(m, n) практически не зависят от объема выборки n, а средние значения P(m) линейно зависят только от числа параметров m регрессионной зависимости (рисунок). На рисунке показана линейная регрессионная зависимость P(m) от m.
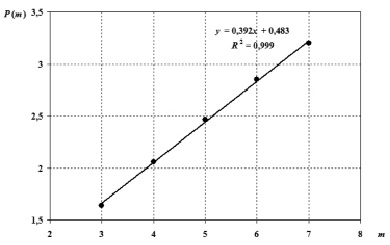
Линейная регрессионная зависимость P(m) от числа параметров m
Для сравнения в табл. 3 приведем отношения средних значений общего количества переходов с одной узловой прямой на другую в статическом случае p0(m, n) (значения взяты из [13]) и в динамическом p(m, n) (табл. 2).
Таблица 3
Отношения p0(m, n)/p(m, n) средних значений общего количества переходов с одной узловой прямой на другую в статическом и в динамическом случаях
|
n |
p0(m, n)/p(m, n) |
||||
|
m = 3 |
m = 4 |
m = 5 |
m = 6 |
m = 7 |
|
|
30 |
3,20 |
3,18 |
3,11 |
3,14 |
3,19 |
|
50 |
3,69 |
3,97 |
4,01 |
4,03 |
4,07 |
|
100 |
4,33 |
4,82 |
5,05 |
5,05 |
5,29 |
|
150 |
4,83 |
5,22 |
5,62 |
5,79 |
5,85 |
|
300 |
5,55 |
6,11 |
6,71 |
6,80 |
7,16 |
|
500 |
6,06 |
6,71 |
7,11 |
7,40 |
7,93 |
|
700 |
6,34 |
7,15 |
7,61 |
8,21 |
8,45 |
|
900 |
6,88 |
7,55 |
8,10 |
8,59 |
9,07 |
|
1000 |
6,63 |
7,68 |
8,14 |
8,70 |
9,46 |
|
1200 |
6,84 |
7,76 |
8,41 |
9,23 |
9,63 |
|
1500 |
7,23 |
8,51 |
8,93 |
9,31 |
10,04 |
|
1700 |
7,15 |
8,28 |
8,97 |
9,74 |
10,20 |
|
1850 |
7,48 |
8,54 |
9,26 |
9,59 |
10,47 |
|
2000 |
7,47 |
8,48 |
9,17 |
10,05 |
10,62 |
Таким образом, получили, что среднее число переходов от одной узловой прямой на другую в предложенном динамическом варианте спуска по узловым прямым составляет O(m). С учетом [10] средняя вычислительная сложность динамического варианта градиентного спуска по узловым прямым составит 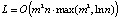 . Если
. Если 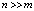 , то
, то 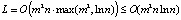 , т.е. выигрыш составил примерно в O(lnn) раз.
, т.е. выигрыш составил примерно в O(lnn) раз.
Заключение
1. Предложенный алгоритм реализации спуска по узловым прямым позволяет повысить быстродействие при решении задач регрессионного моделирования в динамике примерно в O(lnn) раз.
2. Поскольку после удаления на каждом шаге одного наблюдения узловые прямые почти не меняются, следует в дальнейшем также учесть эту особенность рассматриваемой задачи для повышения быстродействия алгоритма.
3. Разработанный алгоритм также позволит повысить быстродействие реализации обобщенного метода наименьших модулей.
Работа выполнена при финансовой поддержке гранта РФФИ, проект № 20-41-660008 р_а.
Библиографическая ссылка
Тырсин А.Н., Голованов О.А. ДИНАМИЧЕСКОЕ РЕГРЕССИОННОЕ МОДЕЛИРОВАНИЕ НА ОСНОВЕ ГРАДИЕНТНОГО СПУСКА ПО УЗЛОВЫМ ПРЯМЫМ // Современные наукоемкие технологии. 2021. № 10. С. 88-93;URL: https://top-technologies.ru/ru/article/view?id=38859 (дата обращения: 06.02.2026).
DOI: https://doi.org/10.17513/snt.38859



