Одной из важных частных задач, возникающих при планировании применения сложных организационно-технических систем (ОТС), является установление рационального сочетания непосредственных технико-технологических операций и процедур контроля их выполнения. Очевидно, что дополнительное уточнение факта выполнения целевой задачи, с одной стороны, повышает степень объективности принимаемого решения, но, с другой стороны, требует использования новых ресурсов и сопровождается временными потерями. Возникает новая научная задача по обоснованию рациональной координации целевых воздействий и процедур контроля.
Анализ предметной области в сфере проблем управления в реальных иерархических системах показал, что методы координации непрерывно развивались в различных работах по исследованию операций. В частности, в работах [1–3] были исследованы два способа организации информационного обмена в процессе координации. Первый предполагает осуществление обмена информацией между центром и подсистемами на каждом шаге итеративного процесса. При втором способе после получения и анализа информации от подсистем центр осуществляет весь итеративный процесс самостоятельно и вырабатывает управляющий сигнал для подсистем. Первый способ позволяет упростить координирующую задачу, но может зависеть от ограниченных вычислительных мощностей и пропускных способностей каналов связи. Второй способ связан с учетом факторов неопределенности, т.е. центр вырабатывает координирующий сигнал, учитывая неопределенность обстановки на основе прогнозирования ее развития; подсистемы действуют и на основе и координирующего сигнала, и реально складывающейся обстановки. Однако в работах [1–3] не предусмотрены вычисления на основе организации ретроспективной развертки поискового процесса, учитывающие результаты контроля состояния ОТС, ошибки распознавания состояния ОТС, а также не учитываются параметры доверительных интервалов исходной информации (об обстановке). Таким образом, необходимо разработать алгоритм управления, учитывающий результаты контроля исполнения управляющих воздействий. При первом подходе к решению данной задачи наиболее адекватной для расчетов моделью представляется схема вероятностной корректировки плана действий по результатам каждого этапа. При втором подходе в качестве модели целесообразно рассматривать марковскую цепь со случайным моментом остановки.
Материалы и методы исследования
Первоначально рассмотрим задачу оптимизации мониторинга результатов применения ОТС на основе пошаговой корректировки плана действий. В методиках и моделях, ориентированных на первый подход, после каждого шага операции по выполнению целевой задачи рассчитываются компоненты корректирующего вектора. Логика оптимизации заключается либо в решении задачи по критерию максимума вероятности достижения требуемого эффекта при жестком ограничении на продолжительность операции и на стоимость дополнительно привлекаемых ресурсов, либо в решении задачи по критерию минимума стоимости дополнительно привлекаемых ресурсов при жестком ограничении на продолжительность операции и на вероятность достижения требуемого эффекта [4; 5]. Однако данные алгоритмы, хотя и отвечают требованию ситуационного реагирования на результаты каждого этапа, не учитывают возросшие возможности перспективных ЭВМ по формированию массива ситуационных решений, соответствующих обстановке. Характеристики компьютеров петафлопсного диапазона и квантовых компьютеров мощностью в несколько кубитов, их оснащение процессорами с архитектурой ARMv9, внедрение алгоритмов Deepfake позволяют осуществлять накапливание и «табулирование» информации по различным исходам каждого шага операции. В связи с этим рассмотрим задачу адаптивного реагирования на результаты этапов при корректировке второго типа, учитывающей реконфигурацию математического ожидания и среднеквадратического отклонения продолжительностей tl не одного, а нескольких последующих этапов (при допущении, что рассматриваемые числовые характеристики величин tl равны их плановым значениям. Вероятностной моделью процесса совместного прохождения процедур контроля и управляющих воздействий при корректировке второго типа является сложная марковская цепь [6]. При этом необходимо предусмотреть, что если полевые исследования или результаты вычислительных экспериментов подтверждают гипотезу о β-распределении продолжительностей этапов, то для получения значений tl, используемых в расчетах, необходимо использовать теорему «Об обратной функции» [7]. Особенности «машинных» аспектов реализации соответствующей имитационной модели будут обусловлены «табличной» спецификой β-распределения, и возникающие при этом «разбросы» получаемых оценок требуют минимизации значений ошибок 1-го и 2-го рода (риска пользователя результатов расчетов и риска исполнителей).
При корректировке первого типа последовательно на каждом этапе, включая предпоследний, рассчитывается вектор реконфигурации, изменяющий параметры распределения продолжительности очередного этапа и минимизирующий стоимость дополнительных инвестиций (выбор из нескольких вариантов, предложенных экспертами и проработанных профильными специалистами); при этом отслеживается выполнение требования по гарантированному обеспечению минимума риска срыва выполнения основной задачи. При корректировке второго типа по результатам каждого этапа для всех остальных шагов, включая предпоследний, рассчитывается вектор реконфигурации, параметры которого последовательно уточняются после окончания каждого этапа путем решения соответствующих оптимизационных задач.
Рассмотрим пример пошаговой оптимизации плана действий при корректировке 2-го типа для случая L = 4. При фактическом выполнении первого этапа за время t1* (например, может иметь место отставание) выражение для продолжительности всей операции уточняется по формуле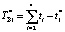 
. Вероятность выполнения задачи в заданный срок Tпл с учетом t1* подлежит пересчету:
,
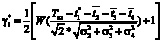где W – табличная функция.
При невыполнении требований руководящих документов (РД), т.е. при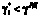 
, необходимо реализовать дополнительные мероприятия, в результате которых произойдет изменение числовых характеристик и второго, и третьего, и четвертого этапов: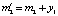 
; 
; 
; 
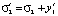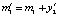
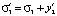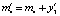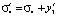. Таким образом, после первого этапа вектор реконфигурации 
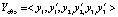имеет размерность 
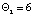и должен удовлетворять ограничению 
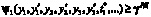или
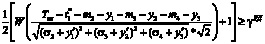
Математическое ожидание затрат на введение в действие обеспечивающих (корректирующих) мероприятий: 
, где x1 = t1* – m1, f – зависимость затрат от с параметров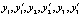 
. Пусть второй этап реализован за время t2 = t2** = f(m2 + y1;
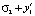). При сохранении отставания и отсутствии временных резервов повторно возникает риск, т.е. при
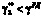, где 
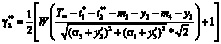
осуществляется новая корректировка, вектор реконфигурации имеет размерность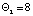 
:
.
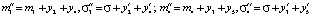Ограничение на вектор реконфигурации: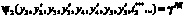 
.
Средние дополнительные затраты от введения в действия мероприятий с параметрами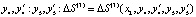 
, где x2 = x1 + y1.
Пусть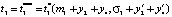 
. При 
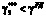, где
,
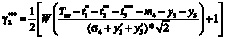осуществляется новая корректировка, вектор реконфигурации имеет размерность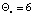 
, при этом
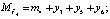
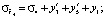т.е.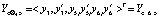 
Ограничение на вектор реконфигурации: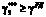 
, где
,
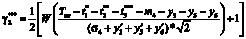или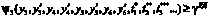 
. Средняя стоимость вводимых резервных ресурсов 
: 
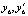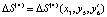, где x3 = x2 + y2 + y4.
Суммарная стоимость всех дополнительно задействуемых ресурсов:
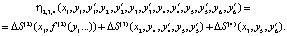
Таким образом, требуется определить такие значения параметров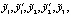 
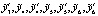, при которых показатель ɳ2,3.4 обращается в минимум и выполняются ограничения:
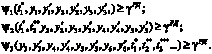
Сформулированная задача решается инерционно с оперативными издержками (временем на сбор информации для регрессионного уточнения коэффициентов зависимости расходов на реконфигурацию от «подбираемых» параметров корректировки).
Результаты исследования и их обсуждение
Для проведения анализа результатов исследования рассмотрим процесс оптимизации мониторинга на основе координации управляющих воздействий и процедур контроля на примере схемы, в которой решение о завершении целенаправленного применения ОТС принимается по результатам проведения контроля факта исполнения управляющей программы [8; 9]. Введем обозначения:
cl – стоимость ресурса, расходуемого на одну попытку целевого воздействия;
h – вероятность реализации одношаговой операции целевого воздействия (например, по переводу из одного штатного режима в другой);
al – стоимость операции контроля состояния ОТС;
B – показатель выходного эффекта (выигрыш от успешного штатного функционирования ОТС; предотвращенный ущерб и т.п.).
Возможны следующие случайные исходы операции: Z1 – задача выполнена с первой попытки; Z2 – процесс проходил по схеме «неудачная попытка → повторная попытка → контроль → удачная попытка → контроль»; Z3 – процесс проходил по схеме «неудачная попытка → контроль → неудачная попытка → контроль → удачная попытка → контроль» и т.д. Исходное множество комбинаций целевых воздействий и процедур контроля определяется экспертами с учетом вероятностно-психологической модели принятия решений (модели действий) операторов.
Для перехода из каждого «нецелевого» состояния (результатов наступления событий Z2, Z3, Z4…) требуется плановый (заранее рассчитанный) расход того или иного ресурса. Так как вероятность перехода процесса из состояния в состояние зависит от результатов предыдущего исхода, то вероятностной моделью рассматриваемого процесса является марковская цепь со случайным моментом остановки [6].
Методика решения задачи включает 3 этапа. Первый этап: генерирование исходного множества альтернатив путем проведения предварительной экспертизы структурных, параметрических и организационных атрибутов вариантов на предмет реализуемости. Второй этап: формирование множества вариантов методом ретроспективной развертки и заполнения базы аналитических решений соответствующих рекуррентных уравнений. Третий этап: определение конкретных комбинаций чередования целевых воздействий и процедур контроля результатов воздействий.
Из вышеизложенного следует, что выигрыш на любом l-м этапе зависит от типа управления. Введём обозначения: K (1) – первый тип управления (воздействие проводится без последующей процедуры распознавания состояния ОТС); K (2) – второй тип (после каждого сеанса проводится контроль факта перехода ОТС в требуемый режим); K (3) – третий тип (проведение управляющих воздействий и процедур контроля прекращается по решению руководства). Найдём связь между средним выигрышем V при нахождении системы в состоянии U(j), j = 0 (1) (L-1) и типом управления. Для первого типа управления Vj,j+1 = – Cl + + B(1 – h)j*h + 0[1 – (1 – h)j*h], но возможен подход, когда вместо нуля подставляются штрафные вычеты. Для второго типа Vj,j+1(K (2)) = – сl – al + B(1 – h)j+1 + 0*[1 – (1 – h)j+1]. Выигрыш для третьего типа управления приравниваем к нулю: Vj,j+1 (K 3)) = 0. Далее, применив принцип проактивного управления для многоэтапной оптимизации и учитывая требование независимости от локальных экстремумов, сформулируем правила согласованного управления для каждого этапа и каждого состояния. В соответствии с логикой учёта возможности любого хода событий первоначально просчитаем выигрыш на последнем этапе. Система после (L-1)-го этапа может находиться либо в состоянии U(L) (цель достигнута), либо в состояниях U (L-1), U (L-2), ... , U ((1), для которых возможна реализация двух типов управления – K(1) и K(3). При применении управления К (1) средний выигрыш на последнем этапе равен
Vl (U ((j), К (1)) = B (1 – h)j*h – al , j = 0 (1)(L – 1).
После алгебраических преобразований получаем рекуррентные выражения для ретроспективной развертки. Если результат (n-1)-го этапа – состояние U (L), то необходимым управляющим воздействием является K(3), т.е. выигрыш на всех оставшихся этапах равен нулю. Если результат (n-1)-го этапа – состояние U(j), j = 0(1)(n-1), то при управлении K(1) выигрыш рассчитывается по формуле
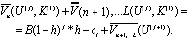
При управлении К(2) в этой же ситуации функциональное уравнение имеет вид
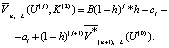
При управлении К(3), если после (n-1)-го этапа наступило состояние U(j), j = 0(1)(n-1), средний выигрыш на всех остальных этапах будет равен нулю. Если по результатам вычислений получаются одинаковые выигрыши, то для отыскания единственного решения необходимо рассчитать среднеквадратическое отклонение как корень второй степени из математического ожидания квадрата центрированного значения выигрыша.
Рассмотрим реализацию алгоритма на примере дистанционного управления и контроля перевода в требуемый режим гипотетической ОТС при следующих исходных данных (в относительных единицах): L = 6; h = 0.3; cl = 1; al = 0.4; B = 8. После вычислений получаем рациональную комбинацию для каждого исхода каждого этапа:
,
,
,
,
,
,
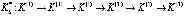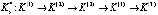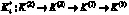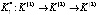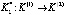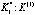при этом максимальный выигрыш составит V* = 3.03. Следует отметить, что при направленном переборе массива параметров исходной информации предлагаемый алгоритм дает возможность проанализировать влияние различных факторов, входящих в состав комплекса исходных данных (соотношение величин L; h; cl; al; B), на степень приближения показателя результативности V* к исходному значению B.
Заключение
Разработаны алгоритмы решения задачи по обоснованию рациональной координации целевых воздействий в процессе применения организационно-технической системы и процедур контроля их результатов. При первом подходе рассматривается сложная марковская цепь со степенью зависимости исходов этапов, определяемой возможностями своевременного создания массива уточненной информации для выбранной схемы. При втором подходе в качестве вероятностной модели рассматривается марковская цепь со случайным моментом остановки; корректировка плана действий по результатам каждого этапа основана на методе стохастического динамического программирования.
Разработанные алгоритмы протестированы на примерах пошаговой корректировки четырехэтапного и шестиэтапного планов (аналитическое и численное решения).
Библиографическая ссылка
Волков В.Ф., Пономарев А.С. ПРИМЕНЕНИЕ МЕТОДА СТОХАСТИЧЕСКОГО ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ ПРИ ОРГАНИЗАЦИИ КОНТРОЛЯ ПРИМЕНЕНИЯ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИХ СИСТЕМ // Современные наукоемкие технологии. – 2021. – № 10. – С. 23-27;URL: https://top-technologies.ru/ru/article/view?id=38849 (дата обращения: 21.11.2024).