Современные методы радиолокации позволяют решать задачу локализации различного рода объектов в условиях, когда использование оптического диапазона не представляется возможным: погодные условия, нахождение объектов в лесном массиве, ночное время суток не позволяют применять оптические сенсоры для определения местоположения людей, техники, объектов инфраструктуры. Однако актуальной является задача распознавания объектов, обнаруженных радиолокационной системой. Решение данной задачи может найти свое применение при поиске наземных транспортных средств в поисково-спасательных операциях и мероприятиях по предотвращению незаконных действий на территории лесных массивов (браконьерство, вырубка леса), а также при классификации воздушных объектов в системах контроля воздушного пространства.
Доплеровский портрет представляет собой частотный спектр сигнала, отраженного от облучаемого объекта, получаемый за счет передвижения цели. Одним из преимуществ использования доплеровского портрета для классификации движущихся целей является простота его векторного представления [1]. С другой стороны, изменение ориентации объекта относительно приемника сигнала, а также изменение скорости движения являются причиной непрерывного изменения принимаемого сигнала во времени. Таким образом, при решении задачи классификации объектов по их доплеровским портретам необходимо учитывать множество изменяемых во времени величин. В настоящее время для решения задач распознавания объектов применяются методы машинного обучения [2–4], позволяющие автоматически построить алгоритм классификации на основании обучающей выборки, содержащей примеры целевых объектов и метки классов, к которым они относятся.
Целью данной работы является разработка алгоритма, позволяющего повысить точность классификации объектов техники по их доплеровским портретам за счет предварительной подготовки исходных данных.
Обзор методов классификации объектов по их доплеровским портретам
Существует ряд методов, позволяющих решать задачу классификации объектов по их доплеровским портретам. В работе [1] представлен подход классификации действий людей (рассматривали бег, спокойный шаг, передвижение ползком) по их доплеровским портретам. В качестве анализируемых признаков авторы использовали среднюю составляющую амплитуды сигнала, максимальное, минимальное и среднее значения для левой и правой огибающих сигнала, ширину полосы пропускания, размах полосы пропускания, размах амплитуды в полосе пропускания, ширину полосы между средними значениями левой и правой огибающих сигнала. В качестве классификатора авторы работы использовали модель k-ближайших соседей (knn) [2].
Еще одним примером распознавания объектов по их доплеровским портретам является работа [3]. В отличие от [5], кроме классификации типов действий (бег, шаг, передвижение ползком), выполняемых одним человеком или группой, перед авторами работы стояла задача распознавания автомобилей и произвольных объектов. В качестве классификатора авторы использовали модифицированную версию нейронной сети AlexNet [4].
Авторы работы [5] также решали задачу классификации объектов, используя сверточную нейронную сеть. Их целью было распознавание малых беспилотных летательных аппаратов (МБЛА) квадрокоптеров и гексакоптеров по их доплеровским портретам. В качестве классификатора авторы работы использовали предобученную модель сверточной нейронной сети GoogLeNet [6], использующую поточечную свертку, позволяющую извлекать признаки, содержащиеся в каналах изображения, не обрабатывая признаки пространственные.
Еще одним примером успешного применения нейронных сетей для распознавания объектов по их доплеровским портретам является работа [7], в которой описан подход, решающий задачу классификации пяти беспилотных летательных аппаратов малых размеров. В качестве классификатора была использована сверточная нейронная сеть на базе архитектуры VGG-16 [8].
В работе [9] для решения задачи классификации объектов по их доплеровским портретам авторы применяли алгоритм обучения без учителя и алгоритм экстремального обучения нейронной сети. Объектами, подлежащими распознаванию, служили 2 типа пешеходов: размахивающий руками и держащий руки в карманах. Аналогично предыдущей рассмотренной работе для извлечений признаков авторы использовали архитектуру VGG-16. Для настройки весов слоев, выполняющих функцию извлечения признаков из доплеровских портретов, представленных в виде изображений, использовался автокодировщик. В свою очередь, в качестве классификатора использовалась extreme learning machine (ELM) [10]. ELM представляет собой полносвязную нейронную сеть, имеющую лишь один скрытый слой. При этом веса входного слоя задаются случайно и не изменяются в процессе обучения модели.
Модели машинного обучения, используемые авторами работ, показатели точности классификации, достигнутые за счет их применения, а также число распознаваемых классов объектов представлены в табл. 1.
Таблица 1
Сравнение результатов рассмотренных исследований
|
Модель |
knn |
AlexNet |
GoogLeNet |
VGG-16 |
ELM |
|
Точность ( %) |
100,0 |
94,2 |
89,3 |
97,7 |
97,0 |
|
Число классов |
3 |
5 |
2 |
5 |
2 |
Исходные данные
Для решения задачи классификации наземных объектов по их доплеровским портретам подготовлена выборка, состоящая из 432 сигналов, отраженных от движущихся объектов девяти классов: БМП, БТР, камаз БОРТОВОЙ, камаз С КУНГОМ, камаз С ПРИЦЕПОМ, ЛЮДИ, САУ, ТАНК, урал С ОРУДИЕМ. Фотографии объектов и их доплеровские портреты представлены на рис. 1.

Рис. 1. Фотографии и доплеровские портреты объектов выборки
На рис. 1 слева направо представлены фотографии (сверху) и доплеровские портреты (снизу) следующих объектов: БМП, КАМАЗ БОРТОВОЙ, БТР. Как видно из рисунка, доплеровские портреты не отражают визуальных характеристик объектов, однако имеют свои отличительные особенности, например: количество центральных и боковых лепестков, их форма и размер, расстояние между ними. Среднее значение объектов обучающей выборки на один класс составило 47, минимальное – 38, максимальное – 60.
Создание обучающей выборки
С помощью преобразования Фурье для каждого сигнала в исходном наборе данных были получены амплитудный и фазовый спектры. Полученные спектры были преобразован в восьмибитные изображения с разрешением 256x250 пикселей. Ось X каждого изображения соответствует частоте сигнала, приведенной к диапазону [0, 255], а ось Y – времени, приведенному к диапазону [0, 250]. Значения амплитуды и фазы приведены к диапазону от 0 до 256 для соответствия значений разрядности изображения. Результат преобразования амплитудного и фазового спектров в изображения представлен на рис. 2.

Рис. 2. Амплитудный (слева) и фазовый (справа) спектры в формате изображения
Полученные пары изображений спектров были перемешаны и разделены на тренировочную и тестовую выборки в соотношении 7:3. Такие пропорции обеспечивают достаточно для обучения модели и ее тестирования количество экземпляров в обучающей и тестовой выборках. Проверка точности работы обученного на тестовой выборке классификатора производилась на данных, не участвовавших в обучении, что обеспечивает оценку обобщающей способности модели и исключает влияние эффекта переобучения на значение показателя точности. Затем была проведена аугментация доплеровских портретов с целью увеличения количества тренировочных и тестовых образцов. В рамках аугментации было проведено отражение каждого изображения доплеровского портрета относительно вертикальной и/или горизонтальной осей. В результате аугментации общее количество тренировочных и тестовых изображений увеличилось в 4 раза и составило 1183 и 509 экземпляров соответственно.
Оценка точности классификации объектов по их доплеровским портретам рассмотренными методами
Авторы рассматриваемых работ для решения задачи классификации объектов по их доплеровским портретам применяли следующие алгоритмы и модели машинного обучения: алгоритм k-ближайших соседей (knn), AlexNet, GoogLeNet, VGG16, ELM на базе VGG16. Для оценки точности работы алгоритма k-ближайших соседей авторы работы [1] извлекли 10 признаков из каждого спектра: средняя составляющяя амплитуды сигнала, максимальное, минимальное и среднее значения левой и правой огибающих сигнала, ширина полосы пропускания, размах амплитуды в полосе пропускания и ширина полосы между средними значениями левой и правой огибающих сигнала. На полученных наборах признаков была проведена оценка точности работы алгоритма со значениями параметра k, находящимися в интервале [2, 10]. Наиболее высокую точность, составившую 49 %, данный алгоритм показал при значении параметра k = 8.
Для оценки точности классификации объектов по их доплеровским портретам были реализованы нейронные сети рассмотренных выше архитектур: AlexNet, GoogLeNet, VGG16. В связи с тем что для обучения сверточных нейронных сетей необходимы колоссальные объемы данных, была применена техника transfer learning [11], суть которой заключается в предварительном обучении нейронной сети на сторонней базе данных большого объема, что позволяет снизить необходимое для тренировки модели количество образцов, а также значительно сокращает количество настраиваемых в ходе обучения параметров нейронной сети. Для оценки эффективности решения задачи классификации объектов были использованы предобученные на наборе данных ImageNet [12] сверточные основы сетей AlexNet, GoogLeNet и VGG16. К каждой из них было добавлено два промежуточных и один выходной полносвязный слои для агрегирования и обработки признаков, извлекаемых предобученными слоями, а также для классификации объекта. Кроме того, на базе нейронной сети со сверточной основой VGG16 была проведена оценка точности работы модели, обученной с помощью метода экстремального обучения (ELM).
Результаты оценки точности классификации объектов на тестовом наборе данных представлены в табл. 2.
Таблица 2
Результаты проверки точности обученных моделей
|
Модель Данные для обучения |
AlexNet ( %) |
GoogLeNet ( %) |
VGG16 ( %) |
ELM ( %) |
knn ( %) |
|
Амплитудный спектр |
13 |
13 |
58 |
51 |
49 |
|
Фазовый спектр |
13 |
13 |
26 |
13 |
- |
Как видно из представленных в табл. 2 данных, фазовый спектр сигнала не содержит признаков, позволяющих произвести классификацию объекта, что объясняется чувствительностью аргумента спектральной функции к смещениям исходного сигнала во времени. Тот факт, что проверка производилась на данных, которых не было в обучающем наборе, говорит о высокой обобщающей способности модели VGG16 при работе с амплитудным спектром сигнала, что подтверждается высоким значением точности модели, обученной с помощью метода экстремального обучения, так как в качестве сверточной основы в ней также использовалась VGG16. ELM, алгоритм k-ближайших соседей и классификаторы на базе AlexNet и GoogLeNet показали меньшее значение точности, чем нейронная сеть на базе VGG16, обученная классическим методом. Таким образом, для классификации объектов по доплеровским портретам целесообразно использовать амплитудный спектр сигнала, а в качестве классификатора из описанных в данной работе моделей наиболее подходящей является нейронная сеть на базе VGG16.
Повышение точности классификации объектов по их доплеровским портретам
Существует ряд методов, позволяющих повысить точность работы моделей классификации. К ним относятся: увеличение объема обучающей выборки, предварительная очистка данных (удаление шумов), снижение размерности исходного пространства признаков.
Авторы работы увеличили объем исходных данных в 4 раза с помощью аугментации изображений доплеровских портретов. Процесс аугментации более подробно описан выше в разделе «Создание обучающей выборки».
Для очистки исходных данных от шумов авторы данной работы использовали свертку исходного сигнала и окна Гаусса, как один из наиболее универсальных методов сглаживания. Применение сглаживания позволило устранить шумы в исходных сигналах, что привело к изменению спектра (рис. 3).
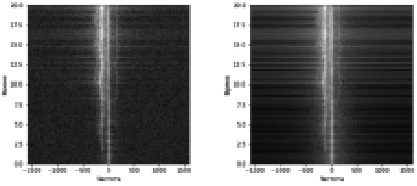
Рис. 3. Амплитудные спектры исходного и сглаженного сигналов
Как видно из рис. 3, сглаживание исходного сигнала повлияло на вид амплитудного спектра: в его боковых частях (справа) наблюдаются четко выраженные линии, соответствующие изменениям значений амплитуды сигнала во временной области, тогда как в боковых частях амплитудного спектра исходного изображения (слева) наблюдается шум.
Для снижения размерности исходного пространства признаков авторами данной работы было выполнено усечение диапазона частот на 70 %. В результате интервал значений частоты амплитудного спектра сигнала сократился до (-560 Гц; 560 Гц), тогда как исходные значения частоты находились в интервале (-1600 Гц; 1600 Гц). За счет этого размер изображения амплитудного спектра сигнала сократился до 78x250 пикселей.
Результаты обучения нейронной сети на предобработанных данных
Использование двух описанных выше методов предобработки позволило получить 3 набора данных. На каждом из наборов была обучена сверточная нейронная сеть на базе VGG16. Результаты оценки точности работы обученных моделей представлены в табл. 3.
Таблица 3
Результаты оценки точности обученных моделей
|
Метод предобработки |
фильтрация |
фильтрация + усечение диапазона частот |
усечение диапазона частот |
|
Точность классификации ( %) |
14 |
78 |
84 |
Данные из табл. 3 позволяют сделать следующие выводы: применение только фильтрации значительно снизило точность работы нейронной сети. В свою очередь, фильтрация и усечение диапазона частот амплитудного спектра повысили точность классификации объектов на 20 %, только усечение диапазона частот – на 26 %. Таким образом, наиболее эффективным методом повышения показателя точности модели в контексте решаемой задачи является снижение размерности исходного пространства признаков.
Результаты оценки точности модели
Усечение диапазона частот амплитудного спектра сигнала позволило увеличить показатель точности работы модели нейронной сети на 26 % по сравнению с моделью, обученной на изображениях исходных амплитудных спектров. Таким образом, усредненная по всем классам объектов точность их распознавания составила 84 %. По полученным в результате тестирования данным, для каждого класса были рассчитаны значения полноты, точности и F-меры. Результаты расчета метрик представлены в табл. 4.
Таблица 4
Значения метрик работы модели
|
Класс Метрика |
САУ |
БМП |
БТР |
Люди |
КАМАЗ БОРТОВОЙ |
КАМАЗ С ПРИЦЕПОМ |
КАМАЗ С КУНГОМ |
УРАЛ С ОРУДИЕМ |
ТАНК |
Среднее значение |
|
Полнота ( %) |
84,48 |
79,07 |
84,44 |
97,78 |
88,33 |
81,48 |
79,17 |
89,58 |
74,24 |
84,29 |
|
Точность ( %) |
81,67 |
70,83 |
82,61 |
91,67 |
88,33 |
84,62 |
88,37 |
86,00 |
81,67 |
83,97 |
|
F-мера ( %) |
83,05 |
74,73 |
83,52 |
94,62 |
88,33 |
83,02 |
83,52 |
87,76 |
77,78 |
84,13 |
По данным, представленным в табл. 4, видно, что наименьшее значение F-меры составило 74,73 % для класса БМП, а наибольшее – 94,62 % для класса ЛЮДИ. Среднее значение F-меры составило 84,13 %, что говорит о достаточно высоком качестве работы обученной модели.
Заключение
В данной работе произведено сравнение показателей точности решения задачи классификации объектов по их доплеровским портретам с помощью алгоритма k-ближайших соседей, сверточных нейронных сетей архитектур AlexNet, GoogLeNet, VGG16, а также алгоритма экстремального обучения сети на основании VGG16. Наиболее успешно в решении данной задачи показала себя нейронная сеть архитектуры VGG16 при использовании в качестве входных данных изображений амплитудного спектра сигнала. В свою очередь, использование фазового спектра дало крайне низкую точность классификации объектов – 13 %, из чего можно сделать вывод о том, что нейронной сети не удается извлечь из него характеристики, позволяющие осуществить классификацию объекта. Данный результат объясняется чувствительностью аргумента спектральной функции к смещению исходного сигнала по оси времени.
Усечение диапазона частот модуля спектральной функции позволило повысить точность работы модели на 26 % по сравнению с использованием исходных амплитудных спектров, что говорит о высокой информативности характеристик центральных лепестков спектра и низкой информативности характеристик боковых.
Предварительное сглаживание исходного сигнала путем свертки его с окном Гаусса снизило точность классификации объектов на 44 % по сравнению с точностью классификации объектов по исходным доплеровским портретам. Данный факт говорит о том, что резкие перепады значений отраженного от объекта сигнала несут в себе полезные признаки, позволяющие классифицировать цель.
Таким образом, наиболее высокое значение точности классификации показала нейронная сеть VGG16. При этом для решения данной задачи целесообразно использовать амплитудный спектр сигнала ввиду наличия в его изображениях признаков, позволяющих нейронной сети определять класс объекта, чей доплеровский объект подается ей на вход. Кроме того, наибольшее количество признаков содержится в центральных лепестках спектра, о чем говорит повышение значения точности работы модели при обработке амплитудного спектра с усеченным диапазоном частот. Также было выявлено, что значительная доля характеристик, позволяющих произвести классификацию объекта по его доплеровскому портрету, содержится в скачкообразных перепадах исходного сигнала.
Библиографическая ссылка
Басов О.О., Толстой И.М., Ле Ань Ту КЛАССИФИКАЦИЯ ДВИЖУЩИХСЯ НАЗЕМНЫХ ОБЪЕКТОВ ПО ИХ ДОПЛЕРОВСКИМ ПОРТРЕТАМ С ПОМОЩЬЮ МЕТОДОВ МАШИННОГО ОБУЧЕНИЯ // Современные наукоемкие технологии. 2021. № 10. С. 17-22;URL: https://top-technologies.ru/ru/article/view?id=38848 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/snt.38848



