Надежность работы в широком диапазоне частот вращения и передаваемых мощностей, высокий КПД, простота обслуживания обусловливают широкое распространение эвольвентных зубчатых передач. Производство зубчатых колес предполагает использование специального оборудования. Ряд современных токарных центров и многокоординатных станков с ЧПУ опционально дают возможность фрезерования зубьев цилиндрических и конических зубчатых колес. Поставщики инструмента [1] предлагают инструмент и услуги по разработке программ для нарезания зубьев на многокоординатных фрезерных станках с ЧПУ и токарных центрах. Для учебных организаций и лабораторий, а также предприятий, не располагающих зубообрабатывающим оборудованием и находящих нецелесообразным воспользоваться услугами специализированных организаций, при необходимости изготовления мелких партий зубчатых колес без повышенных требований по точности актуальна возможность разработки программ по расчетным траекториям движения инструмента – дисковой фрезы, имеющей в диаметральном сечении форму зуба рейки.
Целью исследования является расчет траектории дисковой фрезы с трапецеидальной режущей частью в системе координат, связанной с цилиндрической заготовкой для нарезания прямозубых и косозубых эвольвентных зубчатых колес на токарных центрах и 4-5-координатных фрезерных станках с ЧПУ.
Материалы и методы исследования
Материалом являются стандарты по исходному контуру и методам формообразования зубчатых колес [2, 3], теория эвольвентного зацепления. Методы исследования – аналитика, численные методы для расчета движения инструмента в системе координат, связанной с заготовкой, моделирование в CAD/CAM/CAE системе NX в приложениях «Обработка» и «Симуляция кинематики».
Результаты исследования и их обсуждение
Производится расчет траектории инструмента в системе координат, связанной с заготовкой. Имеем две системы координат. Система O1x1y1z1 – неподвижная система координат, связанная со станком. Относительно данной системы координат осуществляется моделирование воспроизведения реечного зацепления по ГОСТу 13755-2015 [2]. Имеем также систему координат O2x2y2z2 – подвижную, связанную с обрабатываемой заготовкой (рис. 1). В данной системе координат рассчитывается траектория инструмента в процессе формообразования. Заготовка вращается вокруг вертикальной оси O1z1 вместе со связанной системой координат O2x2y2z2 с постоянной угловой скоростью w. На данный момент этап выборки массива материала из впадин зубьев и смещения инструмента вдоль винтовой линии не рассматриваем – фреза движется поступательно в направлении, противоположном оси y1, с постоянной скоростью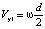 
, где d – делительный диаметр обрабатываемого колеса.
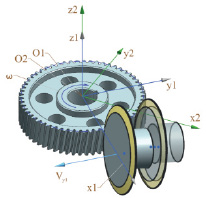
Рис. 1. К расчету траектории инструмента
Если рассматривать плоское сечение, от момента касания режущей кромкой наружной поверхности заготовки до момента выхода этой режущей кромки из заготовки она повернется на угол 2j0 (рис. 2).
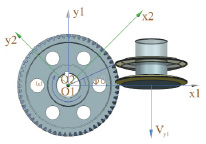
Рис. 2. К определению угла поворота колеса в процессе формообразования
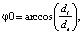
где di – диаметр впадин (диаметр, характеризующий величину врезания) зубчатого колеса, de – диаметр выступов.
При заданной постоянной угловой скорости вращения заготовки w за то же время, как заготовка повернется на угол φ0, точка трассировки фрезы переместится по направлению, противоположному оси O1y1, на расстояние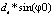 
. Если в качестве точки трассировки фрезы выбрать точку, лежащую на оси вращения фрезы в плоскости пересечения «Конической» и цилиндрической условных поверхностей передней режущей кромки, определить в момент касания начальную координату как y1T0, то координаты точки трассировки в течение времени формообразования будут:
,
,
,
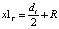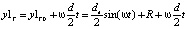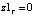где R – радиус фрезы в плоскости расположения точки трассировки, перпендикулярной оси вращения.
Координаты x1T0, z1T0 точки трассировки инструмента в этом случае (в процессе формообразования) остаются неизменными.
В неподвижной системе координат заготовка в момент касания режущей кромкой угловая координата (соответствующая углу собственного вращения вокруг оси z – координате C оборудования с ЧПУ) будет принимать значение j1Д0, с течением времени формообразования данная координата будет изменяться по закону:
Свяжем с неподвижной системой координат орт-векторы i1, j1, k1. С системой координат заготовки (подвижной системой координат) свяжем орт-векторы i2, j2, k2. Будем использовать обращенное движение, т.е. заготовку, и связанную с ним систему координат примем за неподвижную. Вокруг заготовки «вращается» станок с постоянной угловой скоростью w (переносное движение). Относительно станка поступательно движется фреза с постоянной скоростью ωd/2. Отсюда для случая обращенного сложного движения найдем координаты точки трассировки фрезы в системе координат заготовки:
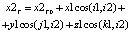
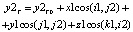
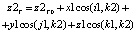
Все косинусы, определяемые относительно орт вектора к1 или к2 (кроме между к1 и к2, равного единице), равны нулю.
,
,
,
.
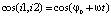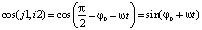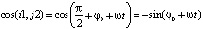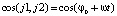Отсюда имеем:
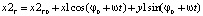
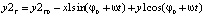
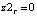
z2T = 0 (в случае отсутствия движения фрезы относительно винтовой линии, образующей зуб).
Помимо координат точки трассировки, для получения траектории инструмента необходимы также координаты вектора ориентации оси вращения инструмента. Эти данные могут быть получены по аналогии с методикой, предложенной в [4]. Фреза в неподвижной системе координат, связанной со станком, движется поступательно. Помимо точки трассировки на фрезе, возьмем точку, лежащую на оси вращения фрезы в плоскости пересечения хвостовика фрезы и торца цанги. Ориентация инструмента в системе координат, связанной с заготовкой, можно определить через разность координат данных двух точек. Расчет может быть выполнен в том числе в электронной таблице. Результат сохраняется в текстовом файле и непосредственно считывается для моделирования траектории.
Профиль режущей части фрезы соответствует профилю зуба рейки лишь в сечении, проходящем через ось вращения фрезы и перпендикулярном направлению (винтовой или прямой линии) зуба. Смещение области формообразования от этой плоскости при повороте на угол α (рис. 3) приведет к увеличению внутреннего диаметра на 2ΔDi и уменьшению ширины впадины на величину Sвп0-Sвп1. Исходя из норм точности зубчатых передач [5] (в данном источнике детально рассматриваются нормы точности зубчатых передач, регламентированные стандартами), требуетcя оценка величины смещения фрезы в направлении зуба либо для следующего прохода, либо одновременно с проходом, рассмотренным выше.
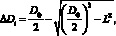
где Dф – максимальный диаметр фрезы в осевом сечении.
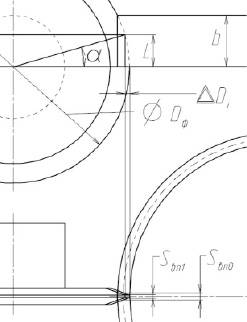
Рис. 3. К оценке величины увеличения внутреннего диаметра и уменьшения ширины впадины
Рис. 4. Результат моделирования обработки впадины зубьев
Результат расчета траектории сохраняется в текстовом файле, где в каждой строке приводятся координаты точки трассировки и координаты вектора ориентации инструмента. Моделирование обработки осуществляется по траектории, с использованием модели фрезы, сохраненной в базе данных. Результат моделирования фрезерования впадины зубьев (без смещения фрезы вдоль направления зуба) представлен на рис. 4.
В приложении «Симуляция кинематики» в качестве звеньев механизма определяем неподвижную стойку, рейку – дисковую фрезу и цилиндрическую заготовку. Заготовка со стойкой образует вращательную пару. Рейка-фреза со стойкой образует поступательную пару. Деталь и рейка образуют реечное зацепление с заданным отношением, обеспечивающим равенство скоростей в точке касания делительной окружности и делительной линии рейки. В предположении относительности воспроизведения движения рейки относительно колеса реализуем трассировку относительного движения фрезы в системе координат, связанной с заготовкой. Результат интерференции фрезы и заготовки сохраняем в виде «Твердого тела». Результат моделирования представлен на рис. 5.
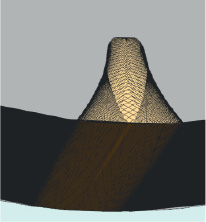
Рис. 5. Результат интерференции модели фрезы и заготовки при воспроизведении реечного зацепления
Результат интерференции представлен набором «твердых тел», создаваемых на каждом расчетном шаге симуляции. Данные твердые тела могут быть объединены в одно, с дальнейшим вычитанием результата из модели заготовки. Результат пригоден для геометрического анализа, моделирования методик контроля, изложенных в [5]. Предварительная оценка результатов моделирования для обработки заготовок диаметром в 1,5-2 раза меньше диаметра фрезы и шириной зубчатого венца 0,5 диаметра заготовки возможна с 4-5 смещениями фрезы вдоль направляющей зуба для класса точности 8. Увеличение норм бокового зазора потребует отдельной обработки боковых поверхностей смежных зубьев.
Выводы
Расчет траектории движения дисковой фрезы, имеющей трапецеидальную режущую часть, соотносимую с профилем рейки (исходного контура), в относительном движении в системе координат цилиндрической заготовки при воспроизведении реечного зацепления позволяет получить координаты управляющей программы для 4-5-координатной обработки прямозубых и косозубых эвольвентных зубчатых колес. Дополнительно при расчете траектории необходимо учитывать нормы точности обрабатываемого зубчатого колеса. При увеличении величины бокового зазора требуется отдельная обработка боковых поверхностей смежных зубьев. Расчет позволяет также учесть смещение исходного контура (корригирование) и при моделировании оценить результат. Расчет траектории может осуществляться с применением, в том числе, электронной таблицы. Сохранение результата расчета в виде файла, где в каждой строке приводятся через пробел числовые значения координат точек трассировки и координат ориентации оси инструмента, позволяет считывать траекторию в CAM-системах и осуществлять ее верификацию.
Библиографическая ссылка
Хасанов Р.Ш., Абзалов А.Р., Асянов Р.Х., Гисматуллин И.М. РАСЧЕТ ТРАЕКТОРИИ ДИСКОВОЙ ФРЕЗЫ С ТРАПЕЦЕИДАЛЬНОЙ РЕЖУЩЕЙ ЧАСТЬЮ ДЛЯ НАРЕЗАНИЯ ЭВОЛЬВЕНТНЫХ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС НА СТАНКАХ С ЧПУ // Современные наукоемкие технологии. – 2021. – № 9. – С. 133-137;URL: https://top-technologies.ru/ru/article/view?id=38825 (дата обращения: 21.11.2024).