Постановка вопроса
Математические методы анализа устойчивости в смысле Ляпунова (кратко – устойчивости) решений обыкновенных дифференциальных уравнений (ОДУ) системно изложены в [1, 2], для класса линейных уравнений – в [3], широко представлены в ряде других классических изданий, их основные применения в теории автоматического управления описаны в [4]. Исследования устойчивости актуальны во многих областях науки, техники и технологии, их незавершенность можно отметить в двух аспектах. Во-первых, известные методы не предлагают универсального анализа устойчивости для различных классов ОДУ. Во-вторых, эти методы, как правило, дают аналитические критерии, непосредственно не предназначенные для численного моделирования и компьютеризации анализа устойчивости. В то же время компьютеризация важна как инструментальное средство для теоретических исследований, для численного и математического моделирования процессов, требующих оценки устойчивости, для решения задач автоматизации управления. Наиболее общие математические методы анализа устойчивости носят характер теорем существования, тогда как для программирования необходима конструктивная форма алгоритмов. Исследования в аспекте алгоритмизации отражены, в частности, в [5, 6], на основе вычисления функций Ляпунова – в [7, 8], однако эти методы не отличает инвариантность относительно класса ОДУ. В излагаемой работе ставится задача представить методы анализа устойчивости, пригодные для компьютерной реализации. Подход основан на инвариантном преобразовании вектор-функции правой части дифференциальной системы, для выполнения которого априори вычисляются производные компонентов по формулам производных сложных функций. Сочетания комбинаций знаков решения и производных позволяет идентифицировать характер устойчивости. Для обоснования подхода необходимо определить условия, при которых асимптотическое стремление к нулю правой части системы влечет сколь угодно малое отклонение решения от нуля либо непосредственное его стремление к нулю. Без искомых условий аналогичные признаки устойчивости [9], представленные для случая автономных систем, не получают корректного обоснования. Как результат исследования предполагается изложить инвариантные формы необходимых и достаточных условий устойчивости на основе знаков решения системы и его двух первых производных, осуществить компьютерную реализацию метода, выполнить численные эксперименты, дать их подробное описание.
Цель исследования
Ставится цель разработать и исследовать компьютерно-ориентированный метод анализа устойчивости решения системы ОДУ по сочетаниям знаков компонентов решения и их производных. Требуется сформулировать и обосновать необходимые и достаточные условия устойчивости, а также асимптотической устойчивости в инвариантной форме, разработать алгоритмизацию и программную реализацию метода на основе приближенного решения системы. Необходимо выполнить численный эксперимент, представить коды программ, дать описание результатов их работы, детально сопоставить данные численного моделирования с аналитическими условиями устойчивости.
Исходные положения
Пусть рассматривается задача Коши для системы ОДУ, имеющей нулевое решение 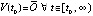 (точку покоя),
(точку покоя),
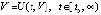 , (1)
, (1)
где 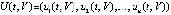 ,
, 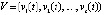 ,
, 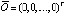 . Пусть требуется исследовать устойчивость точки покоя системы (1). Ниже возмущение
. Пусть требуется исследовать устойчивость точки покоя системы (1). Ниже возмущение 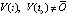 нулевого решения не будет отмечаться специальным знаком. Используются канонические согласованные нормы матрицы и вектора, по умолчанию
нулевого решения не будет отмечаться специальным знаком. Используются канонические согласованные нормы матрицы и вектора, по умолчанию 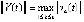 ,
,
в численных экспериментах применяется эвклидова норма 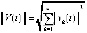 . Относительно (1) предполагается, что существует δ0 > 0, такое, что все условия существования и единственности выполнены для решения и для каждого его возмущения в области
. Относительно (1) предполагается, что существует δ0 > 0, такое, что все условия существования и единственности выполнены для решения и для каждого его возмущения в области 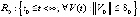 ,
, 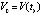 , предполагается, что в этой области вектор-функция U(t, V) определена, непрерывна и удовлетворяет условию Липшица
, предполагается, что в этой области вектор-функция U(t, V) определена, непрерывна и удовлетворяет условию Липшица
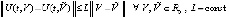 . (2)
. (2)
В данных условиях точка покоя устойчива, если 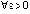 найдется
найдется 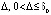 , такое, что
, такое, что 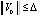 влечет
влечет 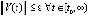 . Точка покоя асимптотически устойчива, если она устойчива и найдется
. Точка покоя асимптотически устойчива, если она устойчива и найдется 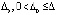 , такое, что из неравенства
, такое, что из неравенства 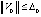 следует
следует 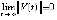 .
.
Условия существования и единственности ниже предполагаются выполненными во всех рассматриваемых случаях, кроме того, наряду с существованием и непрерывностью первой производной 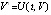 предполагается существование и непрерывность в R0 второй производной решения
предполагается существование и непрерывность в R0 второй производной решения 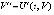 . Эквивалентны обозначения производных
. Эквивалентны обозначения производных 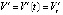 ,
, 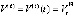 . Производная каждого компонента правой части (1) аналитически определяется по формуле полной производной сложной функции [10]
. Производная каждого компонента правой части (1) аналитически определяется по формуле полной производной сложной функции [10] 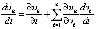 , или
, или
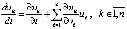 . (3)
. (3)
При оценках асимптотической устойчивости, если 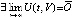 , необходимо указывать, при каких условиях
, необходимо указывать, при каких условиях 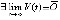 , кратко
, кратко
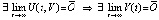 . (4)
. (4)
В [1] аналог (4) используется как очевидное свойство функции Ляпунова, построенной для системы общего вида в рамках теоретико-множественных и пространственно-топологических ограничений, аналогично в [11] – для автономной системы. Для системы (1) условие (4) иногда наглядно, в частности, заведомо выполнено для линейных однородных систем. Однако в общем случае это соотношение требует обоснования и дополнительных ограничений. Ниже (4) записывается по компонентам: 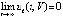
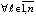 влечет
влечет 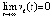
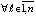 . При оценках неасимптотической устойчивости потребуется аналог (4) с условием достаточной малости ненулевого решения. В дальнейшем всюду, где используется знак нестрогого неравенства относительно vk(t),
. При оценках неасимптотической устойчивости потребуется аналог (4) с условием достаточной малости ненулевого решения. В дальнейшем всюду, где используется знак нестрогого неравенства относительно vk(t), 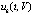 ,
, 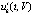 , предполагается, что решения системы (1) исключают каждый из случаев, когда
, предполагается, что решения системы (1) исключают каждый из случаев, когда 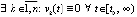 ,
,
а также 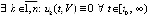 и
и 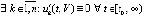 . Иначе знак
. Иначе знак 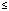 можно было бы толковать в обе противоположные стороны, как и знак
можно было бы толковать в обе противоположные стороны, как и знак 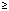 . Для краткости используются обозначения
. Для краткости используются обозначения 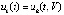 ,
, 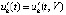
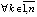 , и иногда
, и иногда 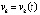 ,
, 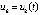 ,
, 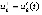 .
.
Условия устойчивости точки покоя системы ОДУ
Имеют место следующие достаточно наглядные утверждения.
Лемма 1. Если 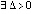 , такое, что
, такое, что 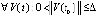 ,
, 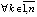 верны неравенства
верны неравенства 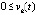 ,
, 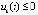
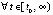 , то точка покоя системы (1) устойчива, кроме того
, то точка покоя системы (1) устойчива, кроме того 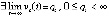 ,
, 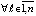 .
.
Доказательство. Пусть 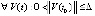 ,
, 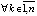 произвольно зафиксировано k = const и выбрано
произвольно зафиксировано k = const и выбрано 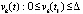 . Функция vk(t) не возрастает (
. Функция vk(t) не возрастает (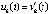 ),
),
поэтому 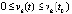
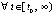 . Отсюда
. Отсюда 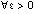 при выборе
при выборе 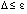 выполнено неравенство
выполнено неравенство 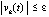
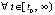 . С учетом произвольности выбора k это означает устойчивость точки покоя. Невозрастающая функция
. С учетом произвольности выбора k это означает устойчивость точки покоя. Невозрастающая функция 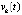 ограничена снизу, поэтому [10]
ограничена снизу, поэтому [10] 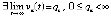
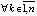 . Лемма доказана.
. Лемма доказана.
Аналогично доказывается
Лемма 2. Если 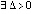 , такое, что
, такое, что 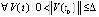 ,
, 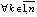 верны неравенства
верны неравенства 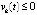 ,
, 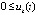
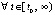 , то точка покоя системы (1) устойчива, кроме того
, то точка покоя системы (1) устойчива, кроме того 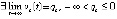 ,
, 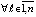 .
.
Если для некоторых 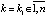 выполнены условия леммы 1, а для всех остальных
выполнены условия леммы 1, а для всех остальных 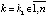 ,
, 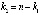 – условия леммы 2, то утверждения обеих лемм обобщает
– условия леммы 2, то утверждения обеих лемм обобщает
Предложение 1. Если 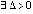 , такое, что
, такое, что 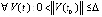 ,
, 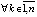 выполняется, не чередуясь при значении k = const, одна из пар неравенств
выполняется, не чередуясь при значении k = const, одна из пар неравенств 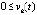 ,
, 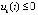 или
или 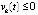 ,
, 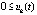
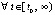 , то точка покоя системы (1) устойчива и
, то точка покоя системы (1) устойчива и 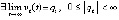 ,
, 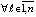 .
.
Имеет место
Предложение 2. Если 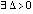 , такое, что
, такое, что 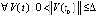 ,
, 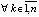 ,
, 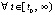 выполняется, возможно, чередуясь при значении k = const, либо пара неравенств
выполняется, возможно, чередуясь при значении k = const, либо пара неравенств 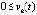 ,
, 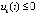 , либо
, либо 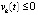 ,
, 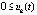 , то точка покоя системы (1) устойчива и
, то точка покоя системы (1) устойчива и 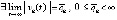
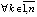 .
.
Доказательство. Пусть 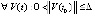 ,
, 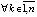 произвольно зафиксировано
произвольно зафиксировано 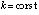 и выбрано
и выбрано 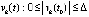 . При выполнении любого сочетания пар неравенств функция
. При выполнении любого сочетания пар неравенств функция 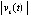 с начальными значениями из
с начальными значениями из 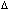 -окрестности нуля не возрастает, поэтому
-окрестности нуля не возрастает, поэтому 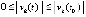
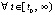 . Отсюда
. Отсюда 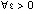 , при выборе
, при выборе 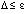 выполнено
выполнено 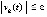
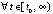 . С учетом произвольности выбора k это означает устойчивость точки покоя. Невозрастающая функция
. С учетом произвольности выбора k это означает устойчивость точки покоя. Невозрастающая функция 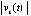 ограничена снизу, поэтому
ограничена снизу, поэтому 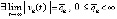
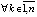 . Лемма доказана.
. Лемма доказана.
Относительно бесконечного чередования пар неравенств при k = const формулируется
Теорема 1. Если 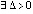 , такое, что
, такое, что 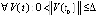 ,
, 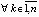 ,
, 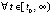 выполняется, бесконечно чередуясь при каждом значении k = const, либо пара неравенств
выполняется, бесконечно чередуясь при каждом значении k = const, либо пара неравенств 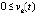 ,
, 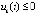 , либо
, либо 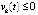 ,
, 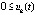 , то точка покоя системы (1) асимптотически устойчива.
, то точка покоя системы (1) асимптотически устойчива.
Доказательство. Поскольку выполнены условия предложения 2, точка покоя системы (1) устойчива. Кроме того 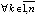 ,
,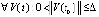
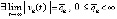 . Если предположить, что
. Если предположить, что 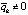 при некотором k = const, то можно взять последовательность точек
при некотором k = const, то можно взять последовательность точек 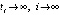 , в каждой из которых
, в каждой из которых 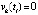 : все такие точки существуют по непрерывности функции vk(t) и бесконечного чередования ее знака. Для взятой последовательности
: все такие точки существуют по непрерывности функции vk(t) и бесконечного чередования ее знака. Для взятой последовательности 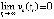 , что противоречит предположению
, что противоречит предположению 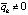 . Предположение неверно, отсюда
. Предположение неверно, отсюда 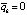 , или
, или 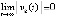
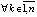 . Следовательно,
. Следовательно, 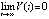
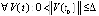 , что означает асимптотическую устойчивость точки покоя. Теорема доказана.
, что означает асимптотическую устойчивость точки покоя. Теорема доказана.
Замечание 1. Как видно из доказательства, утверждение теоремы сохраняется в случае, когда бесконечное чередование пар неравенств при каждом 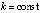 происходит не периодически, но с переменным интервалом времени. Для доказательства требуется только, чтобы чередование на полуоси было бесконечным.
происходит не периодически, но с переменным интервалом времени. Для доказательства требуется только, чтобы чередование на полуоси было бесконечным.
Следствие 1. Пусть точка покоя системы (1) устойчива. Пусть 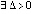 , такое, что
, такое, что 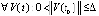 ,
, 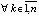 ,
, 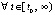 выполняется, бесконечно чередуясь при каждом k = const, либо пара неравенств
выполняется, бесконечно чередуясь при каждом k = const, либо пара неравенств 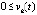 ,
, 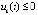 , либо
, либо 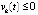 ,
, 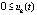 , причем в промежутке между чередованием эти неравенства могут меняться произвольно. Тогда, если
, причем в промежутке между чередованием эти неравенства могут меняться произвольно. Тогда, если 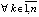
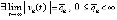 , то точка покоя системы (1) асимптотически устойчива.
, то точка покоя системы (1) асимптотически устойчива.
Доказательство. Существующий по условию предел 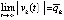 не может быть ненулевым вследствие существования последовательности точек
не может быть ненулевым вследствие существования последовательности точек 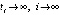 , в каждой из которых
, в каждой из которых 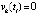 . Поэтому
. Поэтому 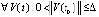 ,
, 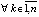 , выполнено
, выполнено 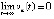 , и точка покоя системы (1) асимптотически устойчива. Следствие доказано.
, и точка покоя системы (1) асимптотически устойчива. Следствие доказано.
Ниже приводятся леммы об асимптотической устойчивости точки покоя в зависимости от асимптотики правой части системы.
Лемма 3. Пусть выполнены условия предложения 2. Если 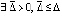 ,
,
такое, что 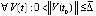 ,
, 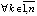
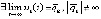 , и кроме того
, и кроме того 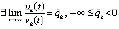 , то точка покоя системы (1) асимптотически устойчива.
, то точка покоя системы (1) асимптотически устойчива.
Доказательство. Поскольку выполнены условия предложения 2, точка покоя устойчива. Пусть 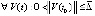 ,
, 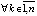 произвольно выбраны
произвольно выбраны 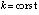 ,
, 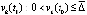 .
.
Вследствие того, что 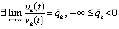 , начиная с некоторого
, начиная с некоторого 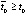 ,
, 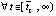 выполняется, не чередуясь (при данном k = const), только одна из пар неравенств:
выполняется, не чередуясь (при данном k = const), только одна из пар неравенств: 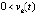 ,
, 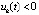 или
или 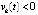 ,
, 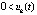 . Пусть рассматривается случай
. Пусть рассматривается случай 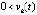 ,
, 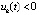
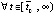 . По условию
. По условию 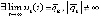 . Если предположить, что
. Если предположить, что 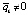 ,
,
то 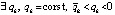 , такое, что, начиная с некоторого
, такое, что, начиная с некоторого 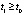 , будет верно неравенство
, будет верно неравенство 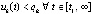 . Тогда
. Тогда 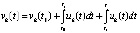 , где
, где 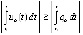 ,
,
и 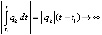 , если
, если 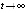 . Отсюда
. Отсюда 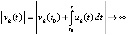 при
при 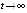 . Радиус
. Радиус 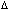 из условия предложения 2 можно считать достаточно малым, чтобы полученное соотношение противоречило устойчивости точки покоя. Предположение неверно, поэтому
из условия предложения 2 можно считать достаточно малым, чтобы полученное соотношение противоречило устойчивости точки покоя. Предположение неверно, поэтому 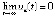 . С учетом этого предела из соотношения
. С учетом этого предела из соотношения 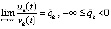 , следует, что
, следует, что 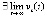 , и порядок малости vk(t) не ниже порядка малости uk(t). Следовательно,
, и порядок малости vk(t) не ниже порядка малости uk(t). Следовательно, 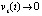 , если
, если 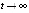 . Аналогично рассматривается случай
. Аналогично рассматривается случай 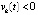 ,
, 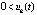
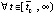 .
.
Ввиду произвольности выбора 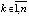 и
и 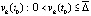 отсюда следует
отсюда следует 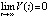
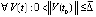 , и точка покоя асимптотически устойчива. Лемма доказана.
, и точка покоя асимптотически устойчива. Лемма доказана.
Лемма 4. Пусть 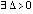 , такое, что
, такое, что 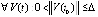 ,
, 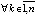 выполняется, возможно, чередуясь при k = const, либо пара неравенств
выполняется, возможно, чередуясь при k = const, либо пара неравенств 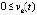 ,
, 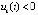 , либо
, либо 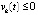 ,
, 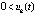
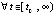 . Точка покоя системы (1) асимптотически устойчива, если чередование этих неравенств бесконечно при каждом
. Точка покоя системы (1) асимптотически устойчива, если чередование этих неравенств бесконечно при каждом 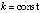 , или если
, или если 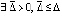 ,
,
такое, что 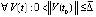 ,
, 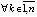
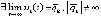 , и, кроме того,
, и, кроме того, 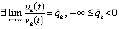 .
.
Доказательство. Поскольку выполнены условия предложения 2, точка покоя системы (1) устойчива. Если при каждом k = const чередование неравенств бесконечно, то асимптотическая устойчивость точки покоя следует из теоремы 1. Если 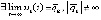 ,
,
и 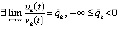
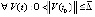 ,
, 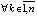 , то асимптотическая устойчивость следует из леммы 3. Лемма доказана.
, то асимптотическая устойчивость следует из леммы 3. Лемма доказана.
Непосредственно ниже представлены условия неустойчивости точки покоя.
Предложение 3. Если 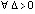
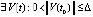 ,
, 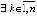 , при которых
, при которых 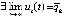 ,
, 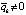 , то точка покоя системы (1) неустойчива.
, то точка покоя системы (1) неустойчива.
Доказательство. Пусть возмущение точки покоя системы (1) рассматривается в случае 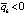 . Тогда
. Тогда 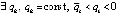 , такое, что, начиная с некоторого
, такое, что, начиная с некоторого 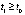 ,
,
будет верно неравенство 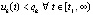 . Отсюда
. Отсюда 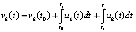 , где
, где 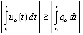 , и
, и 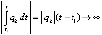 при
при 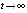 . Поэтому
. Поэтому 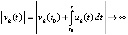 ,
,
если 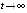 . Радиус Δ можно считать достаточно малым, чтобы это было невозможно, если точка покоя устойчива. Следовательно, в данном случае точка покоя неустойчива. Аналогично, в случае
. Радиус Δ можно считать достаточно малым, чтобы это было невозможно, если точка покоя устойчива. Следовательно, в данном случае точка покоя неустойчива. Аналогично, в случае 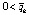 . Рассмотренные соотношения в неравенствах только усилятся, если
. Рассмотренные соотношения в неравенствах только усилятся, если 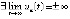 , и в этих случаях точка покоя неустойчива. Предложение доказано.
, и в этих случаях точка покоя неустойчива. Предложение доказано.
Следствие 2. Если 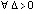
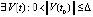 ,
, 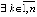 , при которых
, при которых 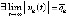 ,
, 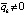 , то точка покоя системы (1) неустойчива. Необходимым условием устойчивости точки покоя является: либо
, то точка покоя системы (1) неустойчива. Необходимым условием устойчивости точки покоя является: либо 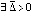 , такое, что
, такое, что 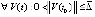 ,
, 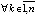
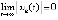 ,
,
либо в любой произвольно малой окрестности нулевого начального вектора найдется решение и такие значения 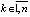 , что для k-х компонентов предел
, что для k-х компонентов предел 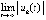 не существует, а для остальных компонентов он равен нулю.
не существует, а для остальных компонентов он равен нулю.
Доказательство разбивается на два случая. Первый – когда, начиная с некоторого 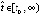 , будет выполняться одно неравенство, для определенности
, будет выполняться одно неравенство, для определенности 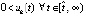 (случай
(случай 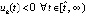 рассматривается аналогично). В этом случае повторяются рассуждения из доказательства предложения 3. Второй – когда uk(t) бесконечно чередует смену знака на противоположный при
рассматривается аналогично). В этом случае повторяются рассуждения из доказательства предложения 3. Второй – когда uk(t) бесконечно чередует смену знака на противоположный при 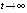 . Но второй случай в данных условиях невозможен, поскольку нашлась бы последовательность точек
. Но второй случай в данных условиях невозможен, поскольку нашлась бы последовательность точек 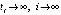 , в каждой из которых
, в каждой из которых 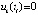 , следовательно,
, следовательно, 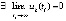 , что противоречит условию
, что противоречит условию 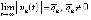 . Необходимое условие устойчивости является отрицанием данного достаточного условия неустойчивости. Следствие доказано.
. Необходимое условие устойчивости является отрицанием данного достаточного условия неустойчивости. Следствие доказано.
Замечание 2. Для асимптотической устойчивости точки покоя системы (1) необходимость 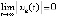
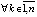 в соответствующей
в соответствующей 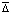 -окрестности следует из (2).
-окрестности следует из (2).
В самом деле, по определению асимптотической устойчивости точки покоя 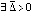 ,
,
такое, что 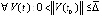 выполнено
выполнено 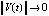 , если
, если 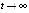 . В случае, когда в (2) сравниваются нулевое решение и его возмущение, с учетом
. В случае, когда в (2) сравниваются нулевое решение и его возмущение, с учетом 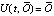 (производная от постоянной функции
(производная от постоянной функции 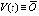 равна нулю) условие Липшица примет вид
равна нулю) условие Липшица примет вид 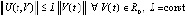 . В рассматриваемой
. В рассматриваемой 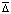 -окрестности предельный переход в неравенстве влечет
-окрестности предельный переход в неравенстве влечет 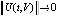 , если
, если 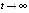 .
.
Имеет место
Предложение 4. Если для системы (1) 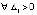
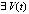 :
: 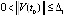 ,
, 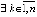 ,
, 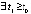 ,
,
такие, что неравенства 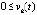 ,
, 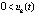 выполнены
выполнены 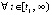 , то точка покоя системы не является асимптотически устойчивой. Аналогично, если
, то точка покоя системы не является асимптотически устойчивой. Аналогично, если 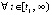 выполнено
выполнено 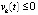 ,
,  .
.
Доказательство. Пусть в условиях предложения 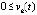 ,
, 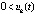
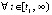 . Какова бы ни была Δ1-окрестность нулевого начального вектора, функция vk(t) возрастает. Если vk(t) ограничена, то
. Какова бы ни была Δ1-окрестность нулевого начального вектора, функция vk(t) возрастает. Если vk(t) ограничена, то 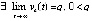 , если vk(t) не ограничена, то
, если vk(t) не ограничена, то 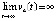 , тогда как для асимптотической устойчивости необходимо существование
, тогда как для асимптотической устойчивости необходимо существование 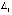 -окрестности нулевого начального вектора, при любом начальном векторе внутри которой
-окрестности нулевого начального вектора, при любом начальном векторе внутри которой 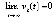 . Аналогично рассматривается случай
. Аналогично рассматривается случай 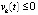 ,
, 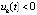
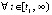 . Предложение доказано.
. Предложение доказано.
Следствие 3. Утверждение предложения 4 сохраняется, если в тех же условиях выполнено либо 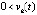 ,
, 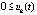
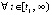 , либо
, либо 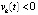 ,
, 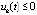
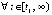 .
.
Доказательство аналогично предыдущему.
Предложение 5. Если для системы (1) 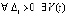 :
: 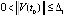 ,
, 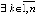 ,
, 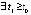 ,
,
такие, что неравенства 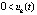 ,
, 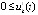 выполнены
выполнены 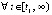 , то точка покоя неустойчива. Аналогично, если
, то точка покоя неустойчива. Аналогично, если 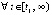 выполнены неравенства
выполнены неравенства 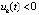 ,
, 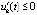 .
.
Доказательство. Пусть рассматривается случай, когда 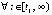 выполнены неравенства
выполнены неравенства 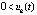 ,
, 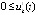 . Аналогично тому, как показано в доказательстве предложения 3, в этом случае
. Аналогично тому, как показано в доказательстве предложения 3, в этом случае 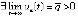 , и в силу этого предложения точка покоя системы (1) неустойчива. Аналогично, если
, и в силу этого предложения точка покоя системы (1) неустойчива. Аналогично, если 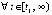 выполнено
выполнено 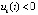 ,
, 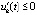 . Предложение доказано.
. Предложение доказано.
Следствие 4. Если для системы (1) 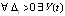 :
: 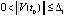 ,
, 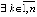 ,
, 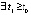 , такие, что
, такие, что 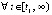 выполняется либо пара неравенств
выполняется либо пара неравенств 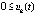 ,
, 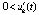 , либо
, либо 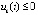 ,
, 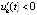 , то точка покоя системы неустойчива.
, то точка покоя системы неустойчива.
Доказательство. Пусть рассматривается случай, когда 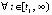 выполнены неравенства
выполнены неравенства 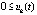 ,
, 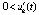 . Если uk(t) ограничена, то с учетом строгого возрастания этой функции
. Если uk(t) ограничена, то с учетом строгого возрастания этой функции 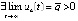 . Если uk(t) не ограничена, то
. Если uk(t) не ограничена, то 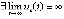 . В обоих случаях точка покоя неустойчива по следствию 2. Аналогично, если
. В обоих случаях точка покоя неустойчива по следствию 2. Аналогично, если 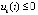 ,
, 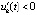 . Следствие доказано.
. Следствие доказано.
Необходимость бесконечного числа совпадений знаков компонентов решения и компонентов его второй производной в случае асимптотической устойчивости точки покоя доказывает
Предложение 6. Пусть точка покоя системы (1) асимптотически устойчива. Тогда, если 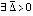 ,
, 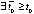 , такие, что
, такие, что 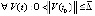 выполняются неравенства
выполняются неравенства 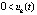 ,
, 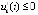
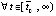 ,
, 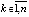 , то
, то 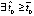 , при котором vk(t) бесконечное число раз принимает значение
, при котором vk(t) бесконечное число раз принимает значение 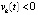 в точках полуоси
в точках полуоси 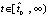 . Если в тех же условиях выполняются неравенства
. Если в тех же условиях выполняются неравенства 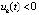 ,
, 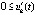 , то
, то 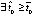 , при котором vk(t) бесконечное число раз принимает значение
, при котором vk(t) бесконечное число раз принимает значение 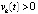 в точках полуоси
в точках полуоси 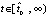 . Если в случае выполнения любой из пар неравенств
. Если в случае выполнения любой из пар неравенств 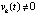
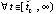 , то
, то 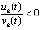
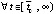 ,
, 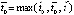 .
.
Доказательство. Пусть в условиях предложения рассматривается случай 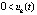 ,
, 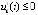 ,
, 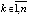 . Если бы выполнялось
. Если бы выполнялось 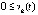
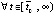 , то в силу
, то в силу 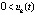 функция vk(t), будучи строго возрастающей, имела бы конечный или бесконечный предел:
функция vk(t), будучи строго возрастающей, имела бы конечный или бесконечный предел: 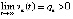 . Но это исключало бы существование
. Но это исключало бы существование 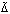 -окрестности (
-окрестности (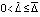 ) нулевого начального вектора, при любых начальных значениях внутри которой должно выполняться
) нулевого начального вектора, при любых начальных значениях внутри которой должно выполняться 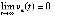
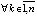 , что необходимо для асимптотической устойчивости. Отсюда в рассматриваемом случае существует
, что необходимо для асимптотической устойчивости. Отсюда в рассматриваемом случае существует 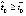 , такое, что vk(t) бесконечное число раз принимает значение
, такое, что vk(t) бесконечное число раз принимает значение 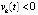 в точках
в точках 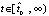 . Если
. Если 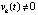
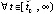 , то по-прежнему не может выполняться
, то по-прежнему не может выполняться 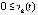 , и vk(t) сохраняет знак
, и vk(t) сохраняет знак 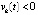 . Отсюда
. Отсюда 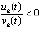
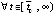 ,
,
где 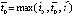 . Случай
. Случай 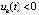 ,
, 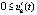 рассматривается аналогично. Предложение доказано.
рассматривается аналогично. Предложение доказано.
Имеет место
Теорема 2. Пусть точка покоя системы (1) устойчива. Тогда, если 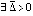 , такое, что
, такое, что 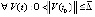 ,
, 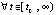 ,
, 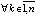 выполняется, возможно чередуясь при k = const, пара неравенств
выполняется, возможно чередуясь при k = const, пара неравенств 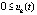 ,
, 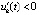 или
или 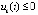 ,
, 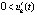 , и кроме того
, и кроме того 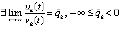 , то точка покоя системы асимптотически устойчива. Утверждение сохраняется, если в тех же условиях выполняется пара неравенств
, то точка покоя системы асимптотически устойчива. Утверждение сохраняется, если в тех же условиях выполняется пара неравенств 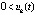 ,
, 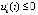 или
или 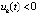 ,
, 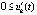 .
.
Доказательство. Пусть произвольно зафиксировано 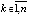 и выбрано
и выбрано 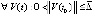 , такое, что
, такое, что 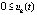 ,
, 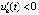 или
или 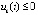 ,
, 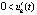
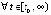 . При выполнении любой данной пары неравенств функция
. При выполнении любой данной пары неравенств функция 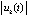 является строго убывающей и ограниченной снизу. Поэтому
является строго убывающей и ограниченной снизу. Поэтому 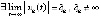 . Если предположить, что
. Если предположить, что 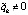 ,
,
то это ведет к противоречию. В самом деле, поскольку 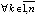
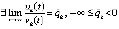 ,
,
то, начиная с некоторого 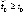 ,
, 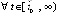 выполняется, не чередуясь при k = const, одна и только одна из пар неравенств:
выполняется, не чередуясь при k = const, одна и только одна из пар неравенств: 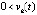 ,
, 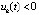 или
или 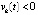 ,
, 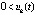 . Иначе можно было бы взять последовательность точек
. Иначе можно было бы взять последовательность точек 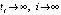 , в каждой из которых
, в каждой из которых 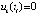 (последовательность
(последовательность 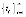 в этом случае существовала бы вследствие непрерывности функции uk(t) и бесконечной чередуемости ее знака), так что
в этом случае существовала бы вследствие непрерывности функции uk(t) и бесконечной чередуемости ее знака), так что 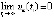 , что противоречило бы предположению
, что противоречило бы предположению 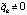 . Тем самым
. Тем самым 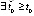 , такое, что знак числителя неизменен
, такое, что знак числителя неизменен 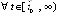 . При стремящейся к отрицательному пределу дроби это влечет противоположный знак знаменателя. В случае, когда для некоторого
. При стремящейся к отрицательному пределу дроби это влечет противоположный знак знаменателя. В случае, когда для некоторого 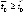 выполнены неравенства
выполнены неравенства 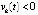 ,
, 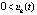
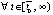 , с учетом
, с учетом 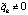 (в данном случае
(в данном случае 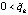 ),
), 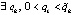 , такое, что, начиная с некоторого
, такое, что, начиная с некоторого 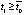 , будет верно неравенство
, будет верно неравенство 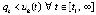 . Тогда
. Тогда 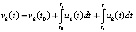 , где
, где 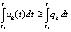 , и
, и 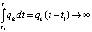 , если
, если 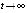 . Но это невозможно, поскольку
. Но это невозможно, поскольку 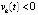
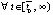 (кроме того,
(кроме того, 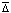 можно считать достаточно малым, чтобы это противоречило устойчивости точки покоя). Случай
можно считать достаточно малым, чтобы это противоречило устойчивости точки покоя). Случай 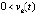 ,
, 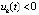
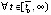 , рассматривается аналогично. В результате предположение
, рассматривается аналогично. В результате предположение 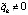 неверно. Следовательно,
неверно. Следовательно, 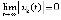 . Таким образом, с учетом произвольности выбора
. Таким образом, с учетом произвольности выбора 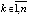 выполнено
выполнено 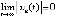
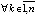 , но тогда и
, но тогда и 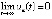
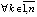 . Отсюда, как и раньше (доказательство леммы 3), соотношение
. Отсюда, как и раньше (доказательство леммы 3), соотношение 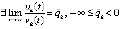
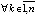 , влечет
, влечет 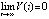 , поэтому точка покоя системы (1) асимптотически устойчива. Теорема доказана.
, поэтому точка покоя системы (1) асимптотически устойчива. Теорема доказана.
Из доказательств теоремы 2 и леммы 3 с учетом предложения 2 выводится
Следствие 5. Пусть 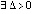 , такое, что
, такое, что 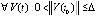 ,
, 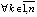 , при каждом
, при каждом 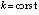 знаки функций vk(t), uk(t),
знаки функций vk(t), uk(t), 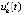 постоянны
постоянны 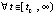 . Тогда для асимптотической устойчивости точки покоя системы (1) необходимо, чтобы
. Тогда для асимптотической устойчивости точки покоя системы (1) необходимо, чтобы 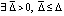 , такое, что
, такое, что 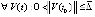 ,
, 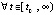 ,
, 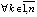 , выполнялись тройки неравенств либо
, выполнялись тройки неравенств либо 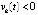 ,
, 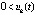 ,
, 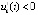 , либо
, либо 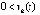 ,
, 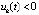 ,
, 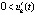 , и, как следствие – неравенства
, и, как следствие – неравенства 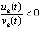 ,
, 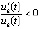 . Если кроме того
. Если кроме того 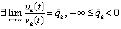 , то все эти условия являются достаточными для асимптотической устойчивости точки покоя.
, то все эти условия являются достаточными для асимптотической устойчивости точки покоя.
В самом деле, в условиях постоянства знаков vk(t), uk(t), 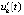 любое нарушение тройки неравенств влечет либо
любое нарушение тройки неравенств влечет либо 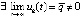 , либо
, либо 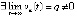 , что исключает асимптотическую устойчивость точки покоя. Напротив, выполнение любой из данных троек неравенств по предложению 2 означает устойчивость, кроме того, влечет, как явствует из доказательства теоремы 2,
, что исключает асимптотическую устойчивость точки покоя. Напротив, выполнение любой из данных троек неравенств по предложению 2 означает устойчивость, кроме того, влечет, как явствует из доказательства теоремы 2, 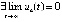 . При условии
. При условии 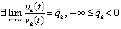 , отсюда следует, как показано в доказательстве леммы 3,
, отсюда следует, как показано в доказательстве леммы 3, 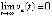 и
и 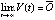 , что означает асимптотическую устойчивость точки покоя.
, что означает асимптотическую устойчивость точки покоя.
Необходимые и достаточные условия асимптотической устойчивости, выраженные через функции правой части системы (1), включают следующие утверждения.
Теорема 3. Пусть точка покоя системы (1) устойчива и 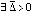 , такое, что
, такое, что 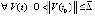 ,
, 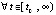 ,
, 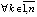 выполняются пары неравенств
выполняются пары неравенств 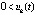 ,
, 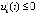 или
или 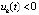 ,
, 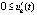 , и кроме того
, и кроме того 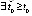 :
: 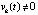
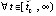 . Тогда для асимптотической устойчивости точки покоя необходимо, чтобы
. Тогда для асимптотической устойчивости точки покоя необходимо, чтобы 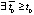 :
: 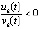
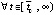 .
.
Если в этих же условиях 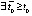 :
: 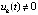
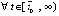 и
и 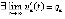
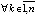 , то необходимым условием асимптотической устойчивости является
, то необходимым условием асимптотической устойчивости является 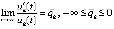 ,
,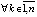 , достаточным условием асимптотической устойчивости является выполнение одновременно двух соотношений:
, достаточным условием асимптотической устойчивости является выполнение одновременно двух соотношений: 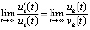 и
и 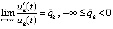 ,
,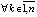 .
.
Доказательство вытекает из следствия 2, предложения 6, теоремы 2 и ее доказательства, согласно которому 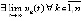 , по следствию 2 этот предел не может быть ненулевым. Если дополнительно
, по следствию 2 этот предел не может быть ненулевым. Если дополнительно 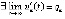
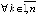 , то с учетом определения асимптотической устойчивости выполнены условия применения правила Лопиталя, отсюда
, то с учетом определения асимптотической устойчивости выполнены условия применения правила Лопиталя, отсюда 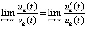
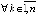 . Для доказательства необходимых условий остается применить утверждение предложения 6, для достаточного условия – утверждение теоремы 2. Теорема доказана.
. Для доказательства необходимых условий остается применить утверждение предложения 6, для достаточного условия – утверждение теоремы 2. Теорема доказана.
Следствие 6. Если соотношение 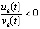
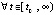 включить в условия теоремы 3, то устойчивость последует из предложения 2, ее предположение в условиях теоремы станет излишним, остальные утверждения не изменятся.
включить в условия теоремы 3, то устойчивость последует из предложения 2, ее предположение в условиях теоремы станет излишним, остальные утверждения не изменятся.
Интегральные условия устойчивости точки покоя. В [9, 12, 13] предложены и обоснованы следующие критерии устойчивости и асимптотической устойчивости точки покоя в изложенных в начале статьи условиях.
Теорема 4. В рассматриваемых условиях для устойчивости точки покоя системы (1) необходимо и достаточно существование 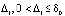 , такого, что
, такого, что 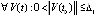 выполняется неравенство
выполняется неравенство
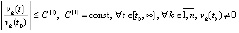 . (5)
. (5)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало 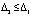 , такое, что
, такое, что 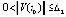 влечет
влечет
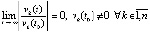 . (6)
. (6)
В (6) деление на 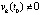 излишне. Однако именно в такой форме информация вводится в компьютер, когда априори неизвестен характер устойчивости точки покоя. В дальнейшем это делается в описании численного эксперимента. Поэтому форма (6) сохраняется ниже для соответствия компьютерному анализу.
излишне. Однако именно в такой форме информация вводится в компьютер, когда априори неизвестен характер устойчивости точки покоя. В дальнейшем это делается в описании численного эксперимента. Поэтому форма (6) сохраняется ниже для соответствия компьютерному анализу.
Критерии теоремы 4 эквивалентны приводимым ниже критериям в интегральной форме.
Теорема 5. В рассматриваемых условиях для устойчивости точки покоя системы (1) необходимо и достаточно существование 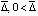 , такого, что
, такого, что 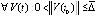 выполняется неравенство
выполняется неравенство
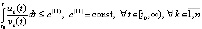 . (7)
. (7)
Для асимптотической устойчивости необходимо и достаточно, чтобы решение было устойчиво и существовало 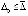 , такое, что
, такое, что 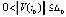 влечет
влечет
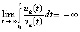
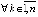 . (8)
. (8)
Обращение в ноль значений знаменателя подынтегральной функции приводит лишь к устранимым особенностям [9], поэтому не влечет некорректности интегрирования. В случае автономных систем знаменатель вообще не обращается в ноль, поскольку различные решения не имеют общих точек [14]. В [13] показано, что теорема 5 следует из теоремы 4. Ниже выполняется обратный вывод, в результате теорема 5 эквивалентна теореме 4. Именно, интеграл в левых частях (7), (8) имеет первообразную: согласно (1) числитель подынтегральной функции есть производная знаменателя, поэтому 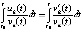 , и
, и 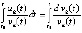 ,
, 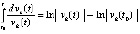 , или,
, или, 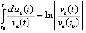 . Отсюда выполнение (7) равносильно выполнению соотношения
. Отсюда выполнение (7) равносильно выполнению соотношения
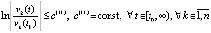 , (9)
, (9)
что имеет место тогда и только тогда, когда
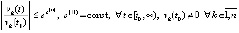 . (10)
. (10)
Таким образом, (5) эквивалентно (7) при 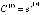 . Аналогично, (8) эквивалентно
. Аналогично, (8) эквивалентно
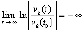
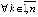 , (11)
, (11)
что возможно тогда и только тогда, когда
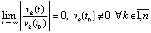 . (12)
. (12)
В итоге (6) эквивалентно (8).
Теорема 5 обобщает рассмотренные отношения знаков решения и производных в качестве условий устойчивости. Так, частный случай условий (7), достаточный для устойчивости точки покоя, заключается в том, что 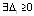 , такое, что
, такое, что 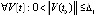 выполняется
выполняется
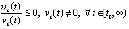 ,
, 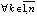 . (13)
. (13)
Условие (13) с некоторыми оговорками равносильно объединению условий лемм 1, 2. Частный случай условий (8), достаточный для асимптотической устойчивости точки покоя – 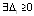 , такое, что
, такое, что 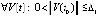 верно неравенство
верно неравенство
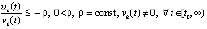 ,
,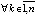 . (14)
. (14)
Условие (14) используется в формулировках теорем 2, 3 и следствия 5. Частный случай условия неустойчивости точки покоя – 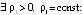
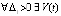 ,
, 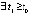 ,
,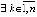 :
: 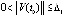 , такие, что
, такие, что
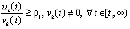 . (15)
. (15)
Условие (15) отчасти используется в предложении 4 и следствии 3.
Замечание 3. Теорема 5 включает не только достаточные, но и необходимые условия, как устойчивости, так и асимптотической устойчивости, представляет собой интегральное обобщение предшествующих утверждений на случай произвольного сочетания и чередования знаков решения и производной. В неявной форме теорема включает содержание всех этих утверждений.
Следствие 7. Если 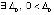 , такое, что
, такое, что 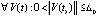 функции vk(t) и uk(t) сохраняют знак
функции vk(t) и uk(t) сохраняют знак 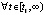 , при этом выполняются неравенства либо
, при этом выполняются неравенства либо 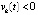 ,
, 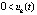 , либо
, либо 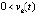 ,
, 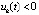
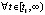 ,
, 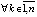 , и, кроме того,
, и, кроме того, 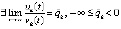 ,
, 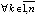 , то точка покоя системы (1) асимптотически устойчива.
, то точка покоя системы (1) асимптотически устойчива.
Доказательство. Поскольку выполнены условия предложения 2, точка покоя устойчива. В условиях следствия 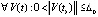
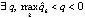 , такое, что, начиная с некоторого
, такое, что, начиная с некоторого 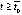 , будет верно неравенство
, будет верно неравенство 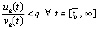 ,
, 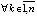 . Кроме того
. Кроме того 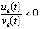
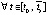 ,
, 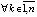 . Согласно теореме Вейерштрасса
. Согласно теореме Вейерштрасса 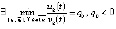 . Отсюда
. Отсюда 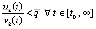 ,
, 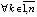 , где
, где 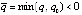 , что влечет (8). Следствие доказано.
, что влечет (8). Следствие доказано.
Аналогичную (7)–(12) схему преобразований можно применить к отношению 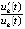 , здесь и ниже предполагается
, здесь и ниже предполагается 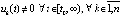 . В результате получится аналог теоремы 5, который не будет использовать выражения компонентов решения vk(t). Очевидно,
. В результате получится аналог теоремы 5, который не будет использовать выражения компонентов решения vk(t). Очевидно, 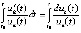 ,
, 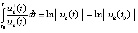 , или,
, или, 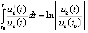 . Аналогично (9), (10) и (11), (12), если выполняется
. Аналогично (9), (10) и (11), (12), если выполняется
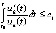 , (16)
, (16)
что равносильно 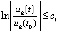 , то тогда и только тогда, когда
, то тогда и только тогда, когда 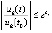 . И если выполняется
. И если выполняется
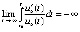 ,
,
что равносильно 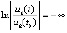 , то в том и только в том случае, когда
, то в том и только в том случае, когда
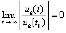 . (17)
. (17)
Эквивалентное (7) условие (5) будет выполняться вследствие выполнения (16), если 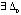 , такое, что
, такое, что 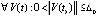 будет обеспечиваться неравенство
будет обеспечиваться неравенство
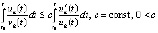
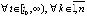 . (18)
. (18)
Частным случаем условия (18) является неравенство, верное 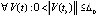 :
:
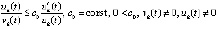
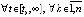 . (19)
. (19)
Имеет место
Теорема 6. При выполнении любого из соотношений (18), (19) для устойчивости точки покоя системы (1) достаточно существование 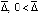 , такого, что
, такого, что 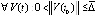 выполняется неравенство
выполняется неравенство
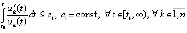 . (20)
. (20)
Для асимптотической устойчивости точки покоя достаточно, чтобы решение было устойчиво и существовало 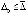 , такое, что
, такое, что 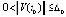 влечет
влечет
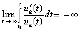
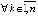 . (21)
. (21)
Доказательство следует из того, что при выполнении любого из условий (18), (19) соотношение (7) – необходимое следствие (20), соотношение (8) – следствие (21).
Как и в случае теорем 4, 5, теорема 6 эквивалентна следующей теореме.
Теорема 7. При выполнении любого из условий (18), (19) для устойчивости точки покоя системы (1) достаточно существование 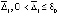 , такого, что
, такого, что 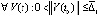 выполняется неравенство
выполняется неравенство
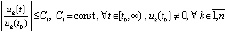 . (22)
. (22)
Для асимптотической устойчивости достаточно, чтобы решение было устойчиво и существовало 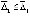 , такое, что
, такое, что 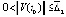 влечет
влечет
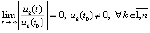 . (23)
. (23)
Следствие 8. Если выполнены условия теоремы 7, то из (23), в эквивалентной форме 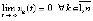 , следует (12), что эквивалентно
, следует (12), что эквивалентно 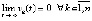 .
.
Замечание 4. В (23) и в (17) можно не использовать деление на 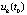 , как и в (6), (11), (12) не использовать деление на
, как и в (6), (11), (12) не использовать деление на 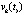 , и можно убрать знак абсолютной величины. Формы (17), (23) используются при вводе-выводе данных в компьютерной реализации метода.
, и можно убрать знак абсолютной величины. Формы (17), (23) используются при вводе-выводе данных в компьютерной реализации метода.
Следствие 9. Пусть для системы (1) 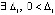 , такое, что
, такое, что 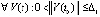 функции uk(t) и
функции uk(t) и 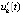 сохраняют знак
сохраняют знак 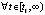 , при этом выполняются неравенства либо
, при этом выполняются неравенства либо 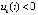 ,
, 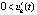 , либо
, либо 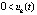 ,
, 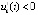
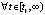 ,
, 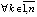 , и кроме того
, и кроме того 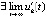 . Тогда точка покоя системы асимптотически устойчива, если выполняется любое одно из двух условий
. Тогда точка покоя системы асимптотически устойчива, если выполняется любое одно из двух условий
1) 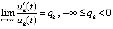 и
и 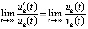
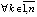 ,
,
2) 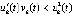 и
и 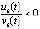
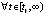 ,
, 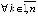 .
.
Доказательство. В первом случае предел существует, поскольку по условию 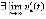 ,
,
а предел знакопостоянной функции uk(t) существует вследствие монотонного убывания 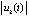 . Достаточно повторить часть рассуждений доказательства следствия 7,
. Достаточно повторить часть рассуждений доказательства следствия 7,
в силу которых 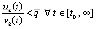 ,
, 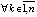 , где
, где 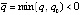 . С учетом условия
. С учетом условия 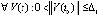 это влечет (7), и точка покоя устойчива. Очевидно, это влечет также (8), что означает ее асимптотическую устойчивость. Во втором случае рассматривается
это влечет (7), и точка покоя устойчива. Очевидно, это влечет также (8), что означает ее асимптотическую устойчивость. Во втором случае рассматривается 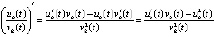 , при этом
, при этом 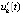 и
и 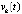 имеют одинаковый знак. Производная отрицательна, если
имеют одинаковый знак. Производная отрицательна, если 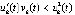 , функция
, функция 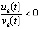 монотонно убывает
монотонно убывает 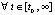 . Отсюда
. Отсюда 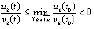 , что с учетом условия обеспечивает выполнение (7) и тем самым устойчивость точки покоя. Последнее неравенство, очевидно, влечет (8), причем согласно условию
, что с учетом условия обеспечивает выполнение (7) и тем самым устойчивость точки покоя. Последнее неравенство, очевидно, влечет (8), причем согласно условию 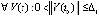 .
.
Следствие доказано.
Замечание 5. Если в условии 2 предполагать устойчивость точки покоя, то условие 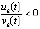
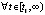 ,
, 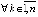 будет выполняться автоматически, напротив, в условиях следствия 9 это неравенство влечет устойчивость по предложению 1.
будет выполняться автоматически, напротив, в условиях следствия 9 это неравенство влечет устойчивость по предложению 1.
Из следствия 9, замечания 5, а также из следствия 5 вытекает
Теорема 8. Пусть для системы (1) 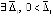 , такое, что
, такое, что 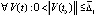 выполняются тройки неравенств либо
выполняются тройки неравенств либо 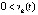 ,
, 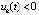 ,
, 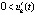 , либо
, либо 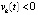 ,
, 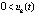 ,
, 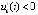
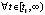 ,
, 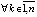 , и кроме того
, и кроме того 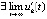 . Тогда точка покоя асимптотически устойчива, если
. Тогда точка покоя асимптотически устойчива, если 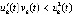
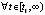 ,
, 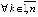 . Если
. Если 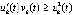
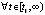 ,
, 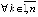 , то достаточным условием асимптотической устойчивости является
, то достаточным условием асимптотической устойчивости является 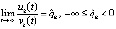 ,
,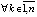 , это же условие достаточно и при
, это же условие достаточно и при 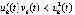 .
.
Интегральные критерии в значительной мере ориентированы на аналитическое применение, что иллюстрируется элементарными примерами, в которых с целью иллюстрации исключено использование аналитического решения. При анализе устойчивости точки покоя ее возмущение ниже рассматривается в предположении 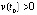 . При написании дроби предполагается, что функция знаменателя не обращается в ноль.
. При написании дроби предполагается, что функция знаменателя не обращается в ноль.
Пример 1. Условиям (18), (19) удовлетворяет уравнение
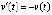 , (24)
, (24)
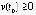 . В самом деле, из (24)
. В самом деле, из (24) 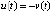 ,
, 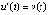 ,
, 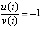 ,
, 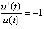 . Отсюда
. Отсюда 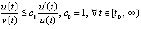 , и применима теорема 6:
, и применима теорема 6: 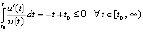 , что согласно (17) означает устойчивость точки покоя. Далее,
, что согласно (17) означает устойчивость точки покоя. Далее, 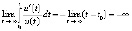 , согласно (18) это влечет асимптотическую устойчивость.
, согласно (18) это влечет асимптотическую устойчивость.
Тот же результат получится другим способом. В силу 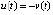 выполнены условия предложения 2, что непосредственно означает устойчивость точки покоя. Вследствие
выполнены условия предложения 2, что непосредственно означает устойчивость точки покоя. Вследствие 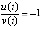 знаки числителя и знаменателя постоянны. По предложению 1
знаки числителя и знаменателя постоянны. По предложению 1 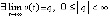 . Отсюда
. Отсюда 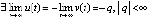 , и
, и 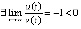 . Выполнены условия леммы 3, это означает асимптотическую устойчивость точки покоя уравнения (21).
. Выполнены условия леммы 3, это означает асимптотическую устойчивость точки покоя уравнения (21).
Еще один способ: в силу 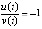 выполнено (14), что является достаточным условием асимптотической устойчивости точки покоя.
выполнено (14), что является достаточным условием асимптотической устойчивости точки покоя.
Пример 2. Рассматривается уравнение
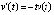 (25)
(25)
при любом 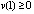 . Из (25)
. Из (25) 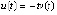 ,
, 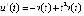 . Далее,
. Далее, 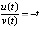 ,
, 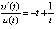 ,
,
и 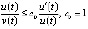 ,
,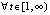 . Применима теорема 6:
. Применима теорема 6: 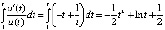 ,
,
и 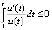
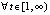 , что согласно (17) означает устойчивость точки покоя. Поскольку
, что согласно (17) означает устойчивость точки покоя. Поскольку 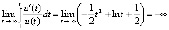 , то согласно (18) точка покоя асимптотически устойчива.
, то согласно (18) точка покоя асимптотически устойчива.
Тот же результат – иначе. В силу 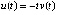 выполнены условия предложения 2, что сразу обеспечивает устойчивость точки покоя. Поскольку
выполнены условия предложения 2, что сразу обеспечивает устойчивость точки покоя. Поскольку 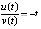 , то
, то 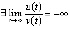 ,
,
что влечет 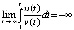 . Согласно (8) точка покоя уравнения (25) асимптотически устойчива.
. Согласно (8) точка покоя уравнения (25) асимптотически устойчива.
Наиболее простой способ: 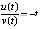 влечет
влечет 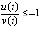
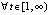 , согласно (14) это достаточное условие асимптотической устойчивости.
, согласно (14) это достаточное условие асимптотической устойчивости.
Пример 3. Рассматривается уравнение
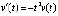 , (26)
, (26)
при любом 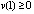 . Из (26)
. Из (26) 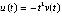 ,
, 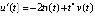 . Отсюда
. Отсюда 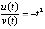 ,
, 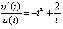 , и
, и 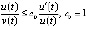 ,
, 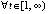 . Применима теорема 6:
. Применима теорема 6: 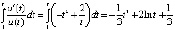 ,
, 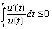
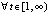 , – точка покоя устойчива. Вследствие
, – точка покоя устойчива. Вследствие 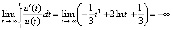 точка покоя асимптотически устойчива. То же получается иначе. В силу
точка покоя асимптотически устойчива. То же получается иначе. В силу 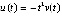 выполнены условия предложения 2, что непосредственно влечет устойчивость точки покоя. Вследствие
выполнены условия предложения 2, что непосредственно влечет устойчивость точки покоя. Вследствие 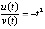
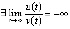 , отсюда
, отсюда 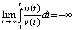 , что согласно (8) означает асимптотическую устойчивость точки покоя уравнения (26). Простейший способ:
, что согласно (8) означает асимптотическую устойчивость точки покоя уравнения (26). Простейший способ: 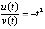
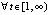 , отсюда
, отсюда 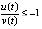
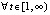 , согласно (14) точка покоя асимптотически устойчива.
, согласно (14) точка покоя асимптотически устойчива.
Пример 4. Пусть рассматривается уравнение
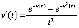 (27)
(27)
при любом 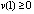 . Из (27)
. Из (27) 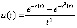 ,
, 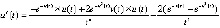 .
.
Отсюда 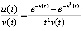 ,
, 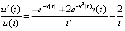 . В этом случае неравенство (19) непосредственно проверить затруднительно, применимость теоремы 6 не получает обоснования. Теорему 5 применить можно, но без специальной оценки интегралов это не влечет правильной оценки устойчивости. Компьютерная реализация критериев (5), (6) теоремы 4 применительно к (27) показывает неасимптотическую устойчивость точки покоя.
. В этом случае неравенство (19) непосредственно проверить затруднительно, применимость теоремы 6 не получает обоснования. Теорему 5 применить можно, но без специальной оценки интегралов это не влечет правильной оценки устойчивости. Компьютерная реализация критериев (5), (6) теоремы 4 применительно к (27) показывает неасимптотическую устойчивость точки покоя.
Пример 5. Рассматривается уравнение
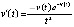 (28)
(28)
при любом 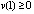 . Из (28)
. Из (28) 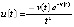 ,
, 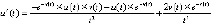 ,
, 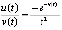 ,
, 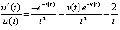 . В этом случае неравенство (19) заведомо не выполняется. Однако устойчивость точки покоя получается согласно предложению 2, поскольку из (28) знаки v(t) и u(t) взаимно противоположны. При этом
. В этом случае неравенство (19) заведомо не выполняется. Однако устойчивость точки покоя получается согласно предложению 2, поскольку из (28) знаки v(t) и u(t) взаимно противоположны. При этом 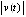 имеет конечный предел при
имеет конечный предел при 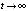 . Следовательно, числитель дроби
. Следовательно, числитель дроби 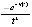 ограничен,
ограничен, 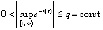 , дробь отрицательна. Тогда интеграл (8) оценивается следующим образом:
, дробь отрицательна. Тогда интеграл (8) оценивается следующим образом: 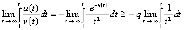 . Отсюда
. Отсюда 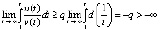 . Это означает, что не выполнено необходимое условие асимптотической устойчивости. Точка покоя уравнения (28) устойчива, но не устойчива асимптотически.
. Это означает, что не выполнено необходимое условие асимптотической устойчивости. Точка покоя уравнения (28) устойчива, но не устойчива асимптотически.
Пример 6. Пусть рассматривается уравнение
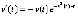 , (29)
, (29)
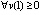 . Из (29)
. Из (29) 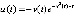 ,
, 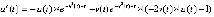 ,
, 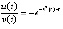 ,
, 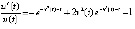 . Функция
. Функция 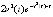 ограничена,
ограничена, 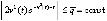 , убывает с ростом t, однако неравенство
, убывает с ростом t, однако неравенство 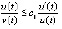
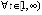 обеспечить затруднительно. Тем не менее устойчивость точки покоя следует из предложения 2, поскольку функции u(t) и v(t) противоположных знаков. Остается проверить (8):
обеспечить затруднительно. Тем не менее устойчивость точки покоя следует из предложения 2, поскольку функции u(t) и v(t) противоположных знаков. Остается проверить (8): 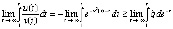 , где
, где 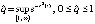 . Тогда
. Тогда 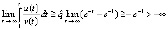 . Это означает, что не выполняется необходимое условие асимптотической устойчивости. Точка покоя устойчива, но неустойчива асимптотически.
. Это означает, что не выполняется необходимое условие асимптотической устойчивости. Точка покоя устойчива, но неустойчива асимптотически.
Пример 7. Рассматривается уравнение
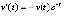 (30)
(30)
при любом 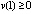 . Из (30)
. Из (30) 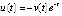 ,
, 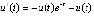 ,
, 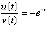 ,
, 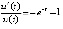 . Знаки u(t) и v(t) противоположны. Согласно предложению 2 точка покоя устойчива. Условие (19) не выполняется. Остается оценить интеграл (8):
. Знаки u(t) и v(t) противоположны. Согласно предложению 2 точка покоя устойчива. Условие (19) не выполняется. Остается оценить интеграл (8): 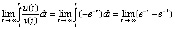 . Отсюда
. Отсюда 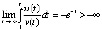 , что нарушает необходимое условие асимптотической устойчивости. Точка покоя устойчива, но не асимптотически.
, что нарушает необходимое условие асимптотической устойчивости. Точка покоя устойчива, но не асимптотически.
Пример 8. Пусть рассматривается уравнение
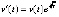 ,
,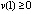 .
.
По условию 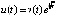 ,
, 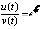 . Отсюда следует (15), поэтому точка покоя неустойчива.
. Отсюда следует (15), поэтому точка покоя неустойчива.
На основе критериев теоремы 6 можно построить аналоги признаков устойчивости, предложенных в [13] для критериев теоремы 5. Имеют место следующие утверждения.
Теорема 9. Если выполнено любое из условий (18) или (19), и, кроме того,
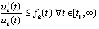 ,
, 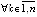 , (31)
, (31)
где 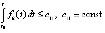 ,
,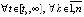 , то точка покоя системы (1) устойчива. В частности утверждение сохраняется, если в (31)
, то точка покоя системы (1) устойчива. В частности утверждение сохраняется, если в (31) 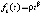 ,
, 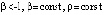 . Если
. Если 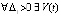 ,
, 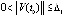 ,
, 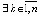 , такие, что
, такие, что 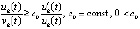 ,
,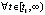 ,
,
и кроме того
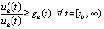 , (32)
, (32)
где 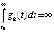 , то точка покоя системы (1) неустойчива. В частности, утверждение сохраняется, если в (32)
, то точка покоя системы (1) неустойчива. В частности, утверждение сохраняется, если в (32) 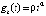 ,
, 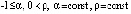 .
.
Замечание 6. Условие во второй части теоремы 9 можно заменить на более общее условие 
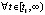 с сохранением утверждения.
с сохранением утверждения.
Теорема 10. Пусть выполнено любое из условий (18) или (19) и точка покоя системы (1) устойчива. Если 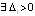 :
: 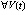 ,
, 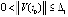 , верно неравенство
, верно неравенство
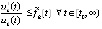 ,
, 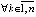 , (33)
, (33)
где 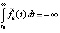 , то точка покоя системы (1) асимптотически устойчива. В частности, утверждение сохраняется, если в (33)
, то точка покоя системы (1) асимптотически устойчива. В частности, утверждение сохраняется, если в (33) 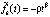 ,
, 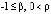 ,
, 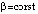 ,
, 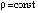 .
.
Доказательства обеих теорем с точностью до обозначений повторяют доказательства соответственных теорем из [13] с той разницей, что учитываются условия (18), (19).
Обсуждение изложенного подхода. Необходимо оговорить зависимости uk(t) и vk(t) в предложенных условиях устойчивости. Одной из целей работы было найти аналитические критерии асимптотической устойчивости, в силу которых из соотношения 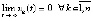 следовало бы
следовало бы 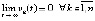 . Иными словами, требовалось обеспечить соотношение (4), позволяющее по поведению правой части (1) судить об устойчивости решения без знания самого решения. В неполной мере соотношение (4) реализовано в леммах 3, 4, предложении 3, следствии 2, предложении 5, следствии 4, предложении 6, теоремах 2, 3, следствии 9, теореме 8. В наибольшей мере выполнение (4) обеспечивают теоремы 6, 7 с использованием (20)–(23). Однако во всех этих случаях утверждения опираются либо на поведение
. Иными словами, требовалось обеспечить соотношение (4), позволяющее по поведению правой части (1) судить об устойчивости решения без знания самого решения. В неполной мере соотношение (4) реализовано в леммах 3, 4, предложении 3, следствии 2, предложении 5, следствии 4, предложении 6, теоремах 2, 3, следствии 9, теореме 8. В наибольшей мере выполнение (4) обеспечивают теоремы 6, 7 с использованием (20)–(23). Однако во всех этих случаях утверждения опираются либо на поведение 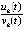 , либо на неравенство
, либо на неравенство 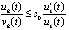 , либо на интегральную форму (18). Тем самым условия выполнения (4) ставятся в зависимость от поведения
, либо на интегральную форму (18). Тем самым условия выполнения (4) ставятся в зависимость от поведения 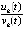 ,
,
в конечном счете – в зависимость от решения. Иногда для аналитической оценки устойчивости можно использовать полученные критерии без знания решения, но это не является общим случаем. Проблема априори неизвестного решения перестает существовать в случае приближенного решения задачи (1). Если, например, задача решается разностным методом, то получается пошаговое приближение решения 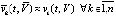 на некотором отрезке
на некотором отрезке 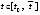 , при этом необходимо используется значение правой части
, при этом необходимо используется значение правой части 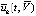 в каждой точке приближения. Пошаговой проверке оказываются доступны условия (5), (6), а также (13)–(15) (в данном приближении). Аналитическое выражение производной правой части вычисляется из (3). Подстановка в выражение
в каждой точке приближения. Пошаговой проверке оказываются доступны условия (5), (6), а также (13)–(15) (в данном приближении). Аналитическое выражение производной правой части вычисляется из (3). Подстановка в выражение 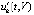 пошаговых приближений
пошаговых приближений 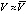 дает значение производной на каждом шаге приближения
дает значение производной на каждом шаге приближения 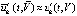 . В результате доступны проверке условия (19), (22), (23), аналогично проверяемы условия большинства предложенных лемм, предложений, теорем и следствий. Значения проверяемых величин выводятся на каждом шаге решения, что дает доступную форму программного анализа устойчивости. Результаты проверки получаются сразу по нескольким критериям. Необходимо отметить два аспекта. Первый – заключается в аналитическом ограничении – формально критерии должны выполняться в некоторой Δ-окрестности начального вектора. Искомая Δ-окрестность программно не идентифицируется. Остается выполнять проверку в выборочных точках этой окрестности. Ускорение процесса с увеличением количества проверочных точек возможно на основе использования параллельной вычислительной системы – синхронный анализ выполним сразу по многим начальным векторам. К отмеченной трудности примыкает еще одна: полуось
. В результате доступны проверке условия (19), (22), (23), аналогично проверяемы условия большинства предложенных лемм, предложений, теорем и следствий. Значения проверяемых величин выводятся на каждом шаге решения, что дает доступную форму программного анализа устойчивости. Результаты проверки получаются сразу по нескольким критериям. Необходимо отметить два аспекта. Первый – заключается в аналитическом ограничении – формально критерии должны выполняться в некоторой Δ-окрестности начального вектора. Искомая Δ-окрестность программно не идентифицируется. Остается выполнять проверку в выборочных точках этой окрестности. Ускорение процесса с увеличением количества проверочных точек возможно на основе использования параллельной вычислительной системы – синхронный анализ выполним сразу по многим начальным векторам. К отмеченной трудности примыкает еще одна: полуось 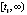 , во всех точках которой требуется выполнение проверяемых условий, по определению не идентифицируется программно. Для имитации полуоси отрезок
, во всех точках которой требуется выполнение проверяемых условий, по определению не идентифицируется программно. Для имитации полуоси отрезок 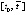 можно удлинять до любой границы
можно удлинять до любой границы 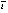 , используя, в частности, методы, описанные в [15, 16]. Помимо того можно выполнять проверочные выборки за пределами границ
, используя, в частности, методы, описанные в [15, 16]. Помимо того можно выполнять проверочные выборки за пределами границ 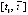 . Во всех случаях нельзя использовать укрупненный шаг разностного метода, чтобы не исказить результаты анализа из-за накопления погрешности. Второй аспект предложенного подхода, напротив, снижает обсуждаемые трудности. Если (1) относится к классу линейных систем, то выполнять проверку критериев в некоторой Δ-окрестности начального вектора не требуется. Как показано в [9] на основе [1], для оценки устойчивости системы (1), если она линейна, достаточно выполнения обсуждаемых критериев для одного произвольно взятого решения со всеми ненулевыми компонентами
. Во всех случаях нельзя использовать укрупненный шаг разностного метода, чтобы не исказить результаты анализа из-за накопления погрешности. Второй аспект предложенного подхода, напротив, снижает обсуждаемые трудности. Если (1) относится к классу линейных систем, то выполнять проверку критериев в некоторой Δ-окрестности начального вектора не требуется. Как показано в [9] на основе [1], для оценки устойчивости системы (1), если она линейна, достаточно выполнения обсуждаемых критериев для одного произвольно взятого решения со всеми ненулевыми компонентами 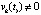
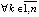 .
.
Вследствие приближенности компьютерного анализа желательно выполнять аналитическое исследование, в частности можно применять предложенные выше методы [9, 13].
Представленные методы относятся к нулевому решению системы (1). Теоретически к этому случаю сводится анализ устойчивости любого ненулевого решения [1]. При описании численных экспериментов будет проиллюстрировано программное сведение анализа устойчивости ненулевого решения к рассмотренным способам анализа нулевого решения.
Численный эксперимент. Пусть рассматривается система
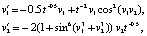 (34)
(34)
где 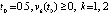 . Требуется исследовать устойчивость точки покоя. Из (34)
. Требуется исследовать устойчивость точки покоя. Из (34) 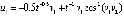 , где обозначено
, где обозначено 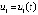 . Аналогично,
. Аналогично, 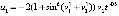 . Согласно (3)
. Согласно (3) 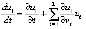 , в данном случае получится
, в данном случае получится
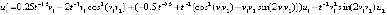 ,
,
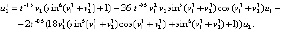
Следующая программа (Delphi) реализует анализ устойчивости точки покоя по знакам решения и двух его производных на основе разностного метода Эйлера.
program RAE11; {$APPTYPE CONSOLE} uses SysUtils;
const h = 0.0001; tt=10000000; var t,v1,v2,eps1,eps2: extended; k: longint;
function u1(t,v1,v2:extended):extended;
begin u1:=-1/2*v1/sqrt(t)+1/sqr(t)*v1*sqr(cos(v1*v2)) end;
function u2(t,v1,v2:extended):extended;
begin u2:=-2/sqrt(t)*v2*(1+ sqr(sqr(sin(sqr(v1)*v1+sqr(v2)*v2)))*
sqr(sin(sqr(v1)*v1+sqr(v2)*v2))) end;
function u11(t,v1,v2:extended):extended;
begin u11:=0.25/(t*sqrt(t))*v1-2/(t*sqr(t))*v1*sqr(cos(v1*v2))+
(-0.5/sqrt(t)+1/sqr(t)*(sqr(cos(v1*v2))-v1*v2* sin(2*v1*v2)))* u1(t,v1,v2)-
1/sqr(t)*sqr(v1)*sin(2*v1*v2)*u2(t,v1,v2) end;
function u21(t,v1,v2:extended):extended;
begin u21:=1/(t*sqrt(t))*v2*(sqr(sin(v1*sqr(v1)+v2*sqr(v2)))*sqr(sqr(sin(v1*sqr(v1)+
v2*sqr(v2))))+1)-36/sqrt(t)*sqr(v1)*v2*sin(v1*sqr(v1)+
v2*sqr(v2))*sqr(sqr(sin(v1*sqr(v1)+v2*sqr(v2))))*cos(v1*sqr(v1)+v2*sqr(v2))*u1(t,v1,v2)-
2/sqrt(t)*(18*v2*sqr(v2)*sin(v1*sqr(v1)+v2*sqr(v2))*sqr(sqr(sin(v1*sqr(v1)+v2*sqr(v2))))*
cos(v1*sqr(v1)+v2*sqr(v2))+sqr(sin(v1*sqr(v1)+v2*sqr(v2)))*
sqr(sqr(sin(v1*sqr(v1)+ v2*sqr(v2))))+1)*u2(t,v1,v2) end;
begin
k := 0; eps1:=0.00005{*0.005}; eps2:=0.00005{*0.005}; v1:=eps1; v2:=eps2; t:=0.5; while t <=10000{00} do
begin v1:= v1+ h * u1(t,v1,v2); v2:= v2+ h * u2(t,v1 ,v2 ); k:=k+1; if k = tt then
begin writeln ('t=',t:4,' '); writeln ('norma=',sqrt(sqr(v1/eps1)+sqr(v2/eps2)):30,' ');
writeln ('v1=',v1:4,' ','u1=',u1(t,v1,v2):4,' ','u11=',u11(t,v1,v2):4,' ','u1/v1=',u1(t,v1,v2)/v1:4,
' ','u11/u1=',u11(t,v1,v2)/u1(t,v1,v2):4,' ','-0.1/sqrt(t)=',-0.1/sqrt(t):4,' ');
writeln ('v2=',v2:4,' ','u2=',u2(t,v1,v2):4,' ','u21=',u21(t,v1,v2):4,' ','u2/v2=',u2(t,v1,v2)/v2:4,
' ','u21/u2=',u21(t,v1,v2)/u2(t,v1,v2):4,' ','-0.1/sqrt(t)=',-0.1/sqrt(t):4,' ');
k:=0 end; t:=t+h; end; readln end.
Результат работы программы:
t= 1.0E+0003 norma= 2.74303107469284169E-0013
v1= 1.3E-0017 u1=-2.2E-0019 u11= 3.5E-0021 u1/v1=-1.6E-0002 u11/u1=-1.6E-0002 -0.1/sqrt(t)=-3.2E-0003
v2= 9.5E-0059 u2=-6.0E-0060 u21= 3.8E-0061 u2/v2=-6.3E-0002 u21/u2=-6.4E-0002 -0.1/sqrt(t)=-3.2E-0003
t= 2.0E+0003 norma= 5.63387098110754843E-0019
v1= 2.8E-0023 u1=-3.1E-0025 u11= 3.6E-0027 u1/v1=-1.1E-0002 u11/u1=-1.1E-0002 -0.1/sqrt(t)=-2.2E-0003
v2= 1.7E-0081 u2=-7.6E-0083 u21= 3.4E-0084 u2/v2=-4.5E-0002 u21/u2=-4.5E-0002 -0.1/sqrt(t)=-2.2E-0003
…………………………………………………………………………………………………………………….
t= 8.0E+0003 norma= 2.13764775102522473E-0038
v1= 1.0E-0042 u1=-6.0E-0045 u11= 3.4E-0047 u1/v1=-5.6E-0003 u11/u1=-5.7E-0003 -0.1/sqrt(t)=-1.1E-0003
v2= 3.5E-0159 u2=-7.8E-0161 u21= 1.8E-0162 u2/v2=-2.2E-0002 u21/u2=-2.2E-0002 -0.1/sqrt(t)=-1.1E-0003
t= 9.0E+0003 norma= 9.41235193418767399E-0041
v1= 4.7E-0045 u1=-2.5E-0047 u11= 1.3E-0049 u1/v1=-5.3E-0003 u11/u1=-5.3E-0003 -0.1/sqrt(t)=-1.0E-0003
v2= 1.3E-0168 u2=-2.8E-0170 u21= 5.9E-0172 u2/v2=-2.1E-0002 u21/u2=-2.1E-0002 -0.1/sqrt(t)=-1.0E-0003
В строке со значением независимой переменной указывается norma – эвклидова норма отношения возмущенного решения к его начальным значениям, вычисляемая из левых частей (5) для применения теоремы 4. В первом слева направо столбце идут компоненты решения в данной точке v1 (v1) и v2 (v2) (округление до двух значащих цифр мантиссы). Во втором столбце – производные компонентов решения u1 (u1) и u2 (u2) (значения правых частей (34) в той же точке). В третьем – производные компонентов правых частей u11 (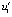 )
)
и u21 (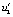 ). В четвертом столбце – отношение компонентов производных к компонентам решения u1/v1 (
). В четвертом столбце – отношение компонентов производных к компонентам решения u1/v1 (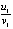 ) и u2/v2 (
) и u2/v2 (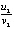 ). В пятом – отношение компонентов вторых производных к компонентам первых производных u11/u1 (
). В пятом – отношение компонентов вторых производных к компонентам первых производных u11/u1 (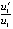 ) и u21/u2 (
) и u21/u2 (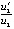 ). Значение элементов шестого столбца будет пояснено ниже. Вычисления выполнялись с шагом h = 10–4 на отрезке
). Значение элементов шестого столбца будет пояснено ниже. Вычисления выполнялись с шагом h = 10–4 на отрезке 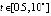 (закомментировано возможное продолжение отрезка). Из представленных данных следует, что значение нормы монотонно убывает до 10–41 (и ниже в продолжении временного отрезка). По теореме 4 согласно (6) это указывает на асимптотическую устойчивость точки покоя. Из расположения в строках видно, что vk и uk, а также
(закомментировано возможное продолжение отрезка). Из представленных данных следует, что значение нормы монотонно убывает до 10–41 (и ниже в продолжении временного отрезка). По теореме 4 согласно (6) это указывает на асимптотическую устойчивость точки покоя. Из расположения в строках видно, что vk и uk, а также 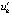 убывают к нулю. При этом vk и uk противоположны по знаку, а vk и
убывают к нулю. При этом vk и uk противоположны по знаку, а vk и 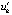 имеют одинаковый знак. По теореме 2, следствию 5, а также по теореме 8 это аналогично указывает на асимптотическую устойчивость точки покоя. Отношения
имеют одинаковый знак. По теореме 2, следствию 5, а также по теореме 8 это аналогично указывает на асимптотическую устойчивость точки покоя. Отношения 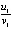 и
и 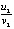 отрицательны и отделены от нуля. Согласно теоремам 2, 3, 5 и соотношению (14) это признаки асимптотической устойчивости. Кроме того, из построчного сопоставления выполнены условия (19) при
отрицательны и отделены от нуля. Согласно теоремам 2, 3, 5 и соотношению (14) это признаки асимптотической устойчивости. Кроме того, из построчного сопоставления выполнены условия (19) при 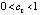 , и применима теорема 6. При этом отношения
, и применима теорема 6. При этом отношения 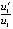 и
и 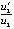 отрицательны и отделены от нуля, отсюда следует (21), что еще раз указывает на асимптотическую устойчивость точки покоя системы (34). Наконец, в шестом столбце данных располагаются значения функции –t–0.5. Из построчного сопоставления видно, что выполняются неравенства (33), коэффициент и показатель степени подбирались по виду предварительно выводившихся значений. По теореме 10 это также является достаточным условием асимптотической устойчивости точки покоя. Все эти соотношения воспроизводятся в качестве признаков асимптотической устойчивости при любом уменьшении радиуса окрестности начальных значений большем нуля (и при любой комбинации их знаков), в частности закомментировано eps1= eps2=0.00005*0.005, а также при удлинении промежутка решения в 100 и более раз. Таким образом, все предложенные признаки в программной реализации указывают на асимптотическую устойчивость точки покоя системы (34). Аналитически этот результат можно получить на основе теоремы 6 аналогично тому, как показано в [9].
отрицательны и отделены от нуля, отсюда следует (21), что еще раз указывает на асимптотическую устойчивость точки покоя системы (34). Наконец, в шестом столбце данных располагаются значения функции –t–0.5. Из построчного сопоставления видно, что выполняются неравенства (33), коэффициент и показатель степени подбирались по виду предварительно выводившихся значений. По теореме 10 это также является достаточным условием асимптотической устойчивости точки покоя. Все эти соотношения воспроизводятся в качестве признаков асимптотической устойчивости при любом уменьшении радиуса окрестности начальных значений большем нуля (и при любой комбинации их знаков), в частности закомментировано eps1= eps2=0.00005*0.005, а также при удлинении промежутка решения в 100 и более раз. Таким образом, все предложенные признаки в программной реализации указывают на асимптотическую устойчивость точки покоя системы (34). Аналитически этот результат можно получить на основе теоремы 6 аналогично тому, как показано в [9].
Пусть рассматривается система
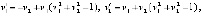 (35)
(35)
где 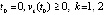 , и требуется исследовать на устойчивость ее точку покоя. Из (35)
, и требуется исследовать на устойчивость ее точку покоя. Из (35)
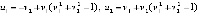 .
.
В силу автономности системы формула (3) примет вид 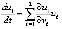 , отсюда
, отсюда
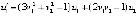 ,
, 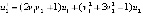 .
.
Чтобы выполнить анализ устойчивости точки покоя, достаточно воспользоваться предыдущей программой RAE11, в которой требуется заменить описание подпрограмм-функций правых частей и их производных на соответствующее описание для рассматриваемой системы:
function u1(t,v1,v2:extended):extended;
begin u1:=-v2+v1*(sqr(v1)+sqr(v2)-1); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1+v2*(sqr(v1)+sqr(v2)-1); end;
function u11 (t,v1,v2:extended):extended;
begin u11:=(3*sqr(v1)+sqr(v2)-1)*u1(t,v1,v2)+(2*v1*v2-1)*u2(t,v1,v2); end;
function u21(t,v1,v2:extended):extended;
begin u21:=(2*v1*v2+1)*u1(t,v1,v2)+(sqr(v1)+3*sqr(v2) -1)*u2(t,v1,v2); end;
Других изменений в программе не потребуется. Результат работы программы:
t= 1.0E+0003 norma= 6.82796739175175673E-0435
v1=-8.1E-0440 u1=-2.5E-0439 u11= 6.6E-0439 u1/v1= 3.1E+0000 u11/u1=-2.6E+0000 -0.1/sqrt(t)=-3.2E-0003
v2= 3.3E-0439 u2=-4.1E-0439 u21= 1.6E-0439 u2/v2=-1.2E+0000 u21/u2=-3.9E-0001 -0.1/sqrt(t)=-3.2E-0003
t= 2.0E+0003 norma= 3.29693623286688257E-0869
v1=-1.6E-0873 u1= 1.1E-0873 u11= 1.0E-0873 u1/v1=-6.8E-0001 u11/u1= 9.4E-0001 -0.1/sqrt(t)=-2.2E-0003
v2= 5.0E-0874 u2=-2.1E-0873 u21= 3.1E-0873 u2/v2=-4.1E+0000 u21/u2=-1.5E+0000 -0.1/sqrt(t)=-2.2E-0003
t= 3.0E+0003 norma= 1.59192352419691632E-1303
v1=-6.0E-1308 u1= 1.1E-1307 u11=-1.0E-1307 u1/v1=-1.9E+0000 u11/u1=-9.3E-0001 -0.1/sqrt(t)=-1.8E-0003
v2=-5.2E-1308 u2=-8.0E-1309 u21= 1.2E-1307 u2/v2= 1.5E-0001 u21/u2=-1.5E+0001 -0.1/sqrt(t)=-1.8E-0003
t= 4.0E+0003 norma= 7.68595824875659265E-1738
v1= 6.4E-1743 u1= 3.1E-1742 u11=-7.6E-1742 u1/v1= 4.9E+0000 u11/u1=-2.4E+0000 -0.1/sqrt(t)=-1.5E-0003
v2=-3.8E-1742 u2= 4.4E-1742 u21=-1.2E-1742 u2/v2=-1.2E+0000 u21/u2=-2.9E-0001 -0.1/sqrt(t)=-1.5E-0003
………………………………………………………………………………………………………………………
t= 9.0E+0003 norma= 0.00000000000000000E+0000
v1=-8.5E-3914 u1= 1.3E-3913 u11=-1.0E-3913 u1/v1=-1.6E+0000 u11/u1=-7.8E-0001 -0.1/sqrt(t)=-1.0E-0003
v2=-5.5E-3914 u2=-3.0E-3914 u21= 1.7E-3913 u2/v2= 5.5E-0001 u21/u2=-5.6E+0000 -0.1/sqrt(t)=-1.0E-0003
t= 1.0E+0004 norma= 0.00000000000000000E+0000
v1= 1.2E-4349 u1= 4.7E-4348 u11=-9.7E-4348 u1/v1= 3.9E+0001 u11/u1=-2.1E+0000 -0.1/sqrt(t)=-1.0E-0003
v2=-4.9E-4348 u2= 5.0E-4348 u21=-2.5E-4349 u2/v2=-1.0E+0000 u21/u2=-4.9E-0002 -0.1/sqrt(t)=-1.0E-0003
Значение нормы монотонно убывает до нуля. По теореме 4 согласно (6) это указывает на асимптотическую устойчивость точки покоя. Из расположения в строках видно, что vk, uk, 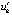 также убывают к нулю, тем самым выполнены необходимые условия устойчивости (следствие 2). Однако в этой задаче vk, uk и
также убывают к нулю, тем самым выполнены необходимые условия устойчивости (следствие 2). Однако в этой задаче vk, uk и 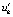 чередуют знаки в произвольном порядке, отношения
чередуют знаки в произвольном порядке, отношения 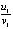 и
и 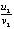 не всегда отрицательны, тем не менее при детальном выводе данных видно соответствие следствию 1, указывающему на асимптотическую устойчивость. Из построчного сопоставления видно, что не выполнены условия (19), поэтому не применима теорема 6, несмотря на то, что отношения
не всегда отрицательны, тем не менее при детальном выводе данных видно соответствие следствию 1, указывающему на асимптотическую устойчивость. Из построчного сопоставления видно, что не выполнены условия (19), поэтому не применима теорема 6, несмотря на то, что отношения 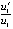 и
и 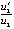 отрицательны и отделены от нуля. Из шестого столбца видно, что выполняются неравенства (33), однако теоремой 10 воспользоваться нельзя ввиду невыполнения (19). Тем не менее на основании просмотра данных следует однозначный вывод. Именно, все данные указывают на выполнение необходимых условий устойчивости, некоторые данные не указывают на выполнение достаточных условий устойчивости. Невыполнение последних не означает отсутствия устойчивости. Аналогичные утверждения можно сделать относительно корреляции данных с асимптотической устойчивостью. В то же время значение нормы вектора компонентов (6) убывает к нулю, означая по теореме 4 выполнение необходимых и достаточных условий асимптотической устойчивости точки покоя. Более того, теорема 4 эквивалентна теореме 5, которая в интегральной оценке учитывает все неочевидные особенности поведения знаков решения и правой части системы. Поэтому выполнение условий (5), (6) является другой (эквивалентной) формой выполнения условий (7), (8), что в любом случае влечет асимптотическую устойчивость точки покоя системы (35). Аналитически полученный результат доказан в [17].
отрицательны и отделены от нуля. Из шестого столбца видно, что выполняются неравенства (33), однако теоремой 10 воспользоваться нельзя ввиду невыполнения (19). Тем не менее на основании просмотра данных следует однозначный вывод. Именно, все данные указывают на выполнение необходимых условий устойчивости, некоторые данные не указывают на выполнение достаточных условий устойчивости. Невыполнение последних не означает отсутствия устойчивости. Аналогичные утверждения можно сделать относительно корреляции данных с асимптотической устойчивостью. В то же время значение нормы вектора компонентов (6) убывает к нулю, означая по теореме 4 выполнение необходимых и достаточных условий асимптотической устойчивости точки покоя. Более того, теорема 4 эквивалентна теореме 5, которая в интегральной оценке учитывает все неочевидные особенности поведения знаков решения и правой части системы. Поэтому выполнение условий (5), (6) является другой (эквивалентной) формой выполнения условий (7), (8), что в любом случае влечет асимптотическую устойчивость точки покоя системы (35). Аналитически полученный результат доказан в [17].
Все рассмотренные соотношения воспроизводятся в качестве признаков асимптотической устойчивости при любых допустимых вариациях радиуса окрестности начальных значений. Удлинить временной отрезок непосредственно при данных параметрах не удается, однако он удлиняется на порядок и больше, если взять h = 10–3, eps1= eps2=0.0005. При этом качественно сохраняются все описанные результаты.
Замечание 7. Именно условия (5), (6), будучи эквивалентными (7), (8) и являясь их доступной программной реализацией, наиболее полно выражают асимптотические особенности поведения знаков решения и его двух производных. При этом (5) неэквивалентно определению устойчивости. Определение требует, чтобы для сколь угодно малого 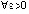 выполнялось
выполнялось 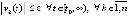 , тогда как (5) требует, чтобы для произвольной (хотя бы сколь угодно большой) константы
, тогда как (5) требует, чтобы для произвольной (хотя бы сколь угодно большой) константы 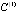 выполнялось неравенство
выполнялось неравенство 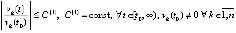 , где
, где 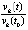 – компонент отношения ненулевого решения к его же начальному значению.
– компонент отношения ненулевого решения к его же начальному значению.
Пусть теперь рассматривается система
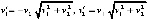 , (36)
, (36)
где 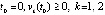 . Требуется исследовать на устойчивость нулевое и ненулевое решение. Из (36)
. Требуется исследовать на устойчивость нулевое и ненулевое решение. Из (36) 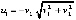 ,
, 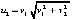 . Отсюда
. Отсюда
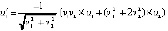 ,
, 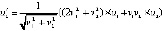 .
.
Чтобы выполнить анализ устойчивости нулевого решения, достаточно воспользоваться той же программой RAE11, в которой следует заменить описание подпрограмм-функций правых частей и их производных на соответствующее описание для системы (36):
function u1(t,v1,v2:extended):extended;
begin u1:=-v2*sqrt(sqr(v1)+sqr(v2)); end;
function u2(t,v1,v2:extended):extended;
begin u2:=v1*sqrt(sqr(v1)+sqr(v2)); end;
function u11 (t,v1,v2:extended):extended;
begin u11:=(-1/sqrt(sqr(v1)+sqr(v2)))*( v1* v2*u1(t,v1,v2)+
(sqr(v1)+2* sqr(v2))*u2(t,v1,v2)); end;
function u21(t,v1,v2:extended):extended;
begin u21:=1/sqrt(sqr(v1)+sqr(v2))*((2*sqr(v1)+sqr(v2))*u1(t,v1,v2)+
v1*v2*u2(t,v1,v2)); end;
Результат работы программы:
t= 1.0E+0003 norma= 1.41421356217253380E+0000
v1= 4.6E-0005 u1=-3.8E-0009 u11=-2.3E-0013 u1/v1=-8.1E-0005 u11/u1= 6.1E-0005 -0.1/sqrt(t)=-3.2E-0003
v2= 5.3E-0005 u2= 3.3E-0009 u21=-2.7E-0013 u2/v2= 6.1E-0005 u21/u2=-8.1E-0005 -0.1/sqrt(t)=-3.2E-0003
t= 2.0E+0003 norma= 1.41421356192948485E+0000
v1= 4.2E-0005 u1=-4.0E-0009 u11=-2.1E-0013 u1/v1=-9.4E-0005 u11/u1= 5.3E-0005 -0.1/sqrt(t)=-2.2E-0003
v2= 5.7E-0005 u2= 3.0E-0009 u21=-2.8E-0013 u2/v2= 5.3E-0005 u21/u2=-9.4E-0005 -0.1/sqrt(t)=-2.2E-0003
t= 3.0E+0003 norma= 1.41421356165181346E+0000
v1= 3.8E-0005 u1=-4.2E-0009 u11=-1.9E-0013 u1/v1=-1.1E-0004 u11/u1= 4.6E-0005 -0.1/sqrt(t)=-1.8E-0003
v2= 5.9E-0005 u2= 2.7E-0009 u21=-3.0E-0013 u2/v2= 4.6E-0005 u21/u2=-1.1E-0004 -0.1/sqrt(t)=-1.8E-0003
……………………………………………………………………………………………………………………..
t= 9.0E+0003 norma= 1.41421355963621205E+0000
v1= 1.0E-0005 u1=-4.9E-0009 u11=-5.2E-0014 u1/v1=-4.7E-0004 u11/u1= 1.0E-0005 -0.1/sqrt(t)=-1.0E-0003
v2= 7.0E-0005 u2= 7.4E-0010 u21=-3.5E-0013 u2/v2= 1.0E-0005 u21/u2=-4.7E-0004 -0.1/sqrt(t)=-1.0E-0003
t= 1.0E+0004 norma= 1.41421355928279811E+0000
v1= 5.5E-0006 u1=-5.0E-0009 u11=-2.8E-0014 u1/v1=-9.0E-0004 u11/u1= 5.5E-0006 -0.1/sqrt(t)=-1.0E-0003
v2= 7.0E-0005 u2= 3.9E-0010 u21=-3.5E-0013 u2/v2= 5.5E-0006 u21/u2=-9.0E-0004 -0.1/sqrt(t)=-1.0E-0003
Значение нормы 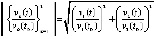 ограничено. Причем ограничение одной и той же константой 1.4142136 неизменно сохраняется при любом уменьшении начальных значений, на несколько порядков включительно. По теореме 4 согласно (5) это указывает на неасимптотическую устойчивость точки покоя. Знаки vk и uk не сохраняются в стабильном состоянии на отрезке решения, равно как и знаки uk и
ограничено. Причем ограничение одной и той же константой 1.4142136 неизменно сохраняется при любом уменьшении начальных значений, на несколько порядков включительно. По теореме 4 согласно (5) это указывает на неасимптотическую устойчивость точки покоя. Знаки vk и uk не сохраняются в стабильном состоянии на отрезке решения, равно как и знаки uk и 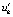 ,
, 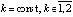 , это проявляется в процессе более подробного вывода данных. Поэтому нельзя применить предложение 4, следствие 3, предложение 5 и следствие 4. Соответственно, нестабильны знаки отношений
, это проявляется в процессе более подробного вывода данных. Поэтому нельзя применить предложение 4, следствие 3, предложение 5 и следствие 4. Соответственно, нестабильны знаки отношений 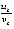 и
и 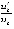 , поэтому неприменимы теорема 3 и соотношения (13)–(15). Проверка того, что
, поэтому неприменимы теорема 3 и соотношения (13)–(15). Проверка того, что 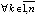
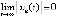 либо
либо 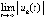 не существует, по данным численного эксперимента оказалась неосуществимой. Поэтому нельзя сослаться на следствие 2. Тем не менее не оказалось данных, которые бы противоречили факту ограниченности
не существует, по данным численного эксперимента оказалась неосуществимой. Поэтому нельзя сослаться на следствие 2. Тем не менее не оказалось данных, которые бы противоречили факту ограниченности 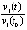 и
и 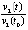 в соотношении (5). Остается принять, что согласно теореме 4 и критерию (5) точка покоя системы (36) неасимптотически устойчива. В [18] это утверждение доказано аналитически.
в соотношении (5). Остается принять, что согласно теореме 4 и критерию (5) точка покоя системы (36) неасимптотически устойчива. В [18] это утверждение доказано аналитически.
Для оценки устойчивости ненулевого решения 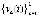 системы (36), программа RAE11 модифицируется таким образом, что вместо исходного возмущения точно такому же анализу подвергается разность между возмущением
системы (36), программа RAE11 модифицируется таким образом, что вместо исходного возмущения точно такому же анализу подвергается разность между возмущением 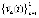 ненулевого решения и самим этим решением, то есть
ненулевого решения и самим этим решением, то есть 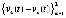 (в программе ниже – компоненты (vv1-v1)
(в программе ниже – компоненты (vv1-v1)
и (vv2-v2)). Соответственно анализируемые производные также переходят в разность производных, 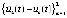 (в программе – u11(t,vv1,vv2)-u11(t,v1,v2) и u21(t,vv1,vv2)-u21(t,v1,v2)), аналогично преобразуются вторые производные и связанные с производными компоненты отношений. В остальном программа RAE11 не меняется, – с точностью до описания новых переменных сохраняется раздел описаний, измененная исполняемая часть программы приводится ниже:
(в программе – u11(t,vv1,vv2)-u11(t,v1,v2) и u21(t,vv1,vv2)-u21(t,v1,v2)), аналогично преобразуются вторые производные и связанные с производными компоненты отношений. В остальном программа RAE11 не меняется, – с точностью до описания новых переменных сохраняется раздел описаний, измененная исполняемая часть программы приводится ниже:
begin
k := 0; eps1:=0.00005; eps2:=0.00005; v1:=1.00005; v2:=1.00005; vv1:=v1+eps1; vv2:=v2+eps2;
t:=0; while t <=10000 do begin
v1:= v1+ h * u1(t,v1,v2); v2:= v2+ h * u2(t,v1 ,v2 ); vv1:= vv1+ h * u1(t,vv1,vv2); vv2:= vv2+ h * u2(t,vv1 ,vv2);
k:=k+1; if k = tt then begin
writeln ('t=',t:4,' '); writeln ('norma=',sqrt(sqr((vv1-v1)/eps1)+sqr((vv2-v2)/eps2)):30,' ');
writeln ('vv1-v1=',vv1-v1:4,' ','uvv1-uv1=',u1(t,vv1,vv2)-u1(t,v1,v2):4,' ',
'uvv11-uv11=',u11(t,vv1,vv2)-u11(t,v1,v2):4,' ','(uvv1-uv1)/(vv1-v1)=',
(u1(t,vv1,vv2)-u1(t,v1,v2))/(vv1-v1):4,' ','(uvv11-uv11)/(uvv1-uv1)=',
(u11(t,vv1,vv2)-u11(t,v1,v2))/(u1(t,vv1,vv2)-u1(t,v1,v2)):4,' ','-0.1/sqrt(t)=',-0.1/sqrt(t):4,' ');
writeln ('vv2-v2=',vv2-v2:4,' ','uvv2-uv2=',u2(t,vv1,vv2)-u2(t,v1,v2):4,' ',
'uvv21-uv21=',u21(t,vv1,vv2)-u21(t,v1,v2):4,' ','(uvv2-uv2)/(vv2-v2)=',
(u2(t,vv1,vv2)-u2(t,v1,v2))/(vv2-v2):4,' ','(uvv21-uv21)/(uvv2-uv2)=',(u21(t,vv1,vv2)-u21(t,v1,v2))/(u2(t,vv1,vv2)-
u2(t,v1,v2)):4,' ','-0.1/sqrt(t)=',-0.1/sqrt(t):4,' ');
k:=0 end; t:=t+h; end; readln
end.
Начальные значения невозмущенного решения взяты для примера v1:=1.00005; v2:=1.00005; остальное все, как в программе RAE11. Результат работы модифицированной программы:
t= 1.0E+0002 norma= 1.98747505986183401E+0002
vv1-v1= 6.1E-0003 uvv1-uv1= 1.1E-0002 uvv11-uv11=-1.1E-0002 (uvv1-uv1)/(vv1-v1)= 1.8E+0000
(uvv11-uv11)/(uvv1-uv1)=-1.1E+0000 -0.1/sqrt(t)=-1.0E-0002
vv2-v2=-7.9E-0003 uvv2-uv2= 8.5E-0003 uvv21-uv21= 1.6E-0002 (uvv2-uv2)/(vv2-v2)=-1.1E+0000
(uvv21-uv21)/(uvv2-uv2)= 1.9E+0000 -0.1/sqrt(t)=-1.0E-0002
t= 2.0E+0002 norma= 3.95033509945234586E+0002
vv1-v1=-3.7E-0003 uvv1-uv1=-2.7E-0002 uvv11-uv11= 7.1E-0003 (uvv1-uv1)/(vv1-v1)= 7.4E+0000
(uvv11-uv11)/(uvv1-uv1)=-2.6E-0001 -0.1/sqrt(t)=-7.1E-0003
vv2-v2= 1.9E-0002 uvv2-uv2=-5.1E-0003 uvv21-uv21=-3.8E-0002 (uvv2-uv2)/(vv2-v2)=-2.6E-0001
(uvv21-uv21)/(uvv2-uv2)= 7.5E+0000 -0.1/sqrt(t)=-7.1E-0003
t= 3.0E+0002 norma= 5.88927116693107776E+0002
vv1-v1=-1.7E-0002 uvv1-uv1= 3.3E-0002 uvv11-uv11= 3.4E-0002 (uvv1-uv1)/(vv1-v1)=-1.9E+0000
(uvv11-uv11)/(uvv1-uv1)= 1.0E+0000 -0.1/sqrt(t)=-5.8E-0003
vv2-v2=-2.4E-0002 uvv2-uv2=-2.4E-0002 uvv21-uv21= 4.7E-0002 (uvv2-uv2)/(vv2-v2)= 1.0E+0000
(uvv21-uv21)/(uvv2-uv2)=-1.9E+0000 -0.1/sqrt(t)=-5.8E-0003
……………………………………………………………………………………………………………
t= 9.9E+0003 norma= 1.17849867942501696E+0004
vv1-v1=-5.7E-0001 uvv1-uv1=-1.6E-0001 uvv11-uv11= 7.7E-0001 (uvv1-uv1)/(vv1-v1)= 2.8E-0001
(uvv11-uv11)/(uvv1-uv1)=-4.7E+0000 -0.1/sqrt(t)=-1.0E-0003
vv2-v2= 1.4E-0001 uvv2-uv2=-6.6E-0001 uvv21-uv21=-1.9E-0001 (uvv2-uv2)/(vv2-v2)=-4.7E+0000
(uvv21-uv21)/(uvv2-uv2)= 2.8E-0001 -0.1/sqrt(t)=-1.0E-0003
t= 1.0E+0004 norma= 1.18511900536141132E+0004
vv1-v1= 3.6E-0001 uvv1-uv1= 5.4E-0001 uvv11-uv11=-4.9E-0001 (uvv1-uv1)/(vv1-v1)= 1.5E+0000
(uvv11-uv11)/(uvv1-uv1)=-9.0E-0001 -0.1/sqrt(t)=-1.0E-0003
vv2-v2=-4.7E-0001 uvv2-uv2= 4.2E-0001 uvv21-uv21= 6.2E-0001 (uvv2-uv2)/(vv2-v2)=-9.0E-0001
(uvv21-uv21)/(uvv2-uv2)= 1.5E+0000 -0.1/sqrt(t)=-1.0E-0003
Значение нормы 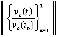 растет от 1.98747505986183401E+0002
растет от 1.98747505986183401E+0002
до 1.18511900536141132E+0004.
Согласно теореме 4 и соотношению (5) точка покоя системы (36) неустойчива. В [18] это утверждение аналитически доказано одновременно для всех ненулевых решений.
Пусть теперь рассматривается линейная однородная система с постоянной матрицей коэффициентов
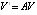 , (37)
, (37)
 . (38)
. (38)
Устойчивость системы будет анализироваться непосредственно по изложенной схеме и по аналогичной программе с той разницей, что уравнений не два, а четыре. Соответственно, должен рассматриваться вектор из четырех компонентов 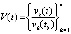 . Для каждого компонента свои первая и вторая производные, и в программе должны быть не две, а четыре подпрограммы-функции, описывающие первые производные, и столько же функций для описания вторых производных. По сути больше ничего в программе не меняется, но требуются две оговорки. Во-первых, производные задаются тривиально, исходя из того, что
. Для каждого компонента свои первая и вторая производные, и в программе должны быть не две, а четыре подпрограммы-функции, описывающие первые производные, и столько же функций для описания вторых производных. По сути больше ничего в программе не меняется, но требуются две оговорки. Во-первых, производные задаются тривиально, исходя из того, что 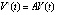 ,
, 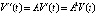 , то есть для задания второй производной требуется квадрат исходной матрицы. Во-вторых, как показано в [9] и отмечалось выше, все рассмотренные критерии устойчивости достаточно применить не к совокупности решений с начальным вектором из окрестности нуля, а к любому одному решению с произвольным начальным вектором, все компоненты которого отличны от нуля. Полученный результат устойчивости или неустойчивости будет означать устойчивость или неустойчивость всей системы [1]. Анализ системы (37) с сохранением обозначений программы RAE11 выполняет следующая программа.
, то есть для задания второй производной требуется квадрат исходной матрицы. Во-вторых, как показано в [9] и отмечалось выше, все рассмотренные критерии устойчивости достаточно применить не к совокупности решений с начальным вектором из окрестности нуля, а к любому одному решению с произвольным начальным вектором, все компоненты которого отличны от нуля. Полученный результат устойчивости или неустойчивости будет означать устойчивость или неустойчивость всей системы [1]. Анализ системы (37) с сохранением обозначений программы RAE11 выполняет следующая программа.
program RAE111111; {$APPTYPE CONSOLE} uses SysUtils;
const n=4; h = 0.0001; tt=100000; type matr=array[1..n,1..n] of extended;
const D:matr=((-1,-0.9, 0.7,-0.1),
(0.8,-0.9, 0.5, 0.2),
(-0.3,0.4,-0.2,-0.6),
(0.7,-0.2,0.9,-1.4));
{D:matr=((1,-0.9, 0.7,-0.1),
(0.8,0.9, 0.5, 0.2),
(-0.3,0.4,0.2,-0.6),
(0.7,-0.2,0.9,1.4));}
var a,a1,c: matr; i,j,l,k: integer; s,t,v1,v2,v3,v4,v10,v20,v30,v40,eps1,eps2,eps3,eps4: extended;
function u1(var a:matr;var t,v1,v2,v3,v4:extended):extended;
begin u1:=a[1,1]*v1+a[1,2]*v2+a[1,3]*v3+a[1,4]*v4; end;
function u2(var a:matr;var t,v1,v2,v3,v4:extended):extended;
begin u2:=a[2,1]*v1+a[2,2]*v2+a[2,3]*v3+a[2,4]*v4; end;
function u3(var a:matr;var t,v1,v2,v3,v4:extended):extended;
begin u3:=a[3,1]*v1+a[3,2]*v2+a[3,3]*v3+a[3,4]*v4; end;
function u4(var a:matr;var t,v1,v2,v3,v4:extended):extended;
begin u4:=a[4,1]*v1+a[4,2]*v2+a[4,3]*v3+a[4,4]*v4; end;
function u11(var a1:matr;var t,v1,v2,v3,v4:extended):extended;
begin u11:=a1[1,1]*v1+a1[1,2]*v2+a1[1,3]*v3+a1[1,4]*v4; end;
function u21(var a1:matr;var t,v1,v2,v3,v4:extended):extended;
begin u21:=a1[2,1]*v1+a1[2,2]*v2+a1[2,3]*v3+a1[2,4]*v4; end;
function u31(var a1:matr;var t,v1,v2,v3,v4:extended):extended;
begin u31:=a1[3,1]*v1+a1[3,2]*v2+a1[3,3]*v3+a1[3,4]*v4; end;
function u41(var a1:matr;var t,v1,v2,v3,v4:extended):extended;
begin u41:=a1[4,1]*v1+a1[4,2]*v2+a1[4,3]*v3+a1[4,4]*v4; end;
begin
for i:=1 to n do for j:=1 to n do begin a[i,j] := D[i,j]; end;
for i := 1 to n do for j := 1 to n do begin s:= 0; for l:= 1 to n do s:= s+a[ i , l ]*a[ l , j ]; a1[i, j]:= s end;
k := 0; eps1:=0.000005; eps2:=0.000005; eps3:=0.000005; eps4:=0.000005; v1:=eps1; v2:=eps2; v3:=eps3; v4:=eps4;
t:=0; while t <=10000 do begin v1:= v1+h*u1(a,t,v1,v2,v3,v4); v2:= v2+h*u2(a,t,v1,v2,v3,v4);
v3:= v3+h*u3(a,t,v1,v2,v3,v4); v4:= v4+h*u4(a,t,v1,v2,v3,v4); k:=k+1; if k=tt then begin
writeln ('t=',t:4,' '); writeln ('norma=',sqrt(sqr(v1/eps1)+sqr(v2/eps2)+sqr(v3/eps3)+sqr(v4/eps4)):30,' ');
writeln ('v1=',v1:4,' ','u1=',u1(a,t,v1,v2,v3,v4):4,' ','u11=',u11(a1,t,v1,v2,v3,v4):4,' ','u1/v1=',
u1(a,t,v1,v2,v3,v4)/v1:4,' ','u11/u1=',u11(a1,t,v1,v2,v3,v4)/u1(a,t,v1,v2,v3,v4):4,' ','-0.1/sqrt(t)=',-20/sqrt(t):4,' ');
writeln ('v2=',v2:4,' ','u2=',u2(a,t,v1,v2,v3,v4):4,' ','u21=',u21(a1,t,v1,v2,v3,v4):4,' ','u2/v2=',
u2(a,t,v1,v2,v3,v4)/v2:4,' ','u21/u2=',u21(a1,t,v1,v2,v3,v4)/u2(a,t,v1,v2,v3,v4):4,' ','-0.1/sqrt(t)=',-20/sqrt(t):4,' ');
writeln ('v3=',v3:4,' ','u3=',u3(a,t,v1,v2,v3,v4):4,' ','u31=',u31(a1,t,v1,v2,v3,v4):4,' ','u3/v3=',
u3(a,t,v1,v2,v3,v4)/v3:4,' ','u31/u3=',u31(a1,t,v1,v2,v3,v4)/u3(a,t,v1,v2,v3,v4):4,' ','-0.1/sqrt(t)=',-20/sqrt(t):4,' ');
writeln ('v4=',v4:4,' ','u4=',u4(a,t,v1,v2,v3,v4):4,' ','u41=',u41(a1,t,v1,v2,v3,v4):4,' ','u4/v4=',
u4(a,t,v1,v2,v3,v4)/v4:4,' ','u41/u4=',u41(a1,t,v1,v2,v3,v4)/u4(a,t,v1,v2,v3,v4):4,' ','-0.1/sqrt(t)=',-20/sqrt(t):4,' ');
k:=0 end; t:=t+h; end; readln end.
Результат работы программы:
t= 1.0E+0001 norma= 1.78676640589015832E-0001
v1=-5.3E-0008 u1= 1.0E-0008 u11=-2.8E-0009 u1/v1=-2.0E-0001 u11/u1=-2.6E-0001 -0.1/sqrt(t)=-6.3E+0000
v2= 5.0E-0007 u2=-1.0E-0007 u21= 2.0E-0008 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-6.3E+0000
v3= 6.4E-0007 u3=-1.3E-0007 u31= 2.7E-0008 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-6.3E+0000
v4= 3.7E-0007 u4=-7.4E-0008 u41= 1.4E-0008 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-6.3E+0000
t= 2.0E+0001 norma= 2.33223801465169568E-0002
v1=-6.9E-0009 u1= 1.4E-0009 u11=-2.9E-0010 u1/v1=-2.0E-0001 u11/u1=-2.0E-0001 -0.1/sqrt(t)=-4.5E+0000
v2= 6.6E-0008 u2=-1.3E-0008 u21= 2.7E-0009 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-4.5E+0000
v3= 8.3E-0008 u3=-1.7E-0008 u31= 3.5E-0009 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-4.5E+0000
v4= 4.8E-0008 u4=-9.7E-0009 u41= 2.0E-0009 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-4.5E+0000
……………………………………………………………………………………………………………………...
t= 2.7E+0003 norma= 1.07878879748941343E-0236
v1=-3.2E-0243 u1= 6.5E-0244 u11=-1.3E-0244 u1/v1=-2.0E-0001 u11/u1=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v2= 3.0E-0242 u2=-6.2E-0243 u21= 1.3E-0243 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v3= 3.9E-0242 u3=-7.9E-0243 u31= 1.6E-0243 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v4= 2.2E-0242 u4=-4.5E-0243 u41= 9.1E-0244 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
t= 2.7E+0003 norma= 1.40816655776991311E-0237
v1=-4.2E-0244 u1= 8.5E-0245 u11=-1.7E-0245 u1/v1=-2.0E-0001 u11/u1=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v2= 4.0E-0243 u2=-8.1E-0244 u21= 1.6E-0244 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v3= 5.0E-0243 u3=-1.0E-0243 u31= 2.1E-0244 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
v4= 2.9E-0243 u4=-5.9E-0244 u41= 1.1E-0244 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-3.9E-0001
…………………………………………………………………………………………………………………….
t= 1.0E+0004 norma= 5.47291005571722000E-0884
v1=-1.6E-0890 u1= 3.3E-0891 u11=-6.7E-0892 u1/v1=-2.0E-0001 u11/u1=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v2= 1.5E-0889 u2=-3.1E-0890 u21= 6.4E-0891 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v3= 2.0E-0889 u3=-4.0E-0890 u31= 8.1E-0891 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v4= 1.1E-0889 u4=-2.3E-0890 u41= 4.6E-0891 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
t= 1.0E+0004 norma= 7.14390892089263713E-0885
v1=-2.1E-0891 u1= 4.3E-0892 u11=-8.7E-0893 u1/v1=-2.0E-0001 u11/u1=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v2= 2.0E-0890 u2=-4.1E-0891 u21= 8.3E-0892 u2/v2=-2.0E-0001 u21/u2=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v3= 2.6E-0890 u3=-5.2E-0891 u31= 1.0E-0891 u3/v3=-2.0E-0001 u31/u3=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
v4= 1.5E-0890 u4=-3.0E-0891 u41= 6.1E-0892 u4/v4=-2.0E-0001 u41/u4=-2.0E-0001 -0.1/sqrt(t)=-2.0E-0001
Относительно полученных данных можно повторить сказанное относительно данных анализа системы (34): на примере системы (37) с матрицей (38) подтверждаются все предложенные признаки асимптотической устойчивости. В частности, норма 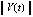 монотонно убывает до 10–885, что согласно (6) указывает на асимптотическую устойчивость точки покоя. Компоненты vk, uk,
монотонно убывает до 10–885, что согласно (6) указывает на асимптотическую устойчивость точки покоя. Компоненты vk, uk, 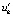 убывают к нулю. При этом vk и
убывают к нулю. При этом vk и 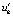 всегда имеют одинаковый знак, который проти-
всегда имеют одинаковый знак, который проти-
воположен знаку uk, что согласно следствию 5
и теореме 8 также указывает на асимптотическую устойчивость. Отношения 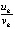 отрицательны и отделены от нуля, это означает признак асимптотической устойчивости. Выполнены условия (19),
отрицательны и отделены от нуля, это означает признак асимптотической устойчивости. Выполнены условия (19), 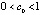 , и применима теорема 6, причем
, и применима теорема 6, причем 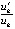 отрицательны и отделены от нуля, отсюда следует (21), также указывая на асимптотическую устойчивость. В шестом столбце значения функции
отрицательны и отделены от нуля, отсюда следует (21), также указывая на асимптотическую устойчивость. В шестом столбце значения функции 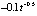 , из строк видно, что выполняется (33), по теореме 10 это еще одно условие асимптотической устойчивости. Таким образом, все признаки в программной реализации указывают на асимптотическую устойчивость системы (37) с матрицей (38). Если в этой матрице изменить на противоположный знак верхнего элемента главной диагонали, как закомментировано в программе, и повторить программу с полученной матрицей, то возникнет переполнение. Если сократить отрезок решения в 10 раз, то выходные данные покажут критический рост нормы
, из строк видно, что выполняется (33), по теореме 10 это еще одно условие асимптотической устойчивости. Таким образом, все признаки в программной реализации указывают на асимптотическую устойчивость системы (37) с матрицей (38). Если в этой матрице изменить на противоположный знак верхнего элемента главной диагонали, как закомментировано в программе, и повторить программу с полученной матрицей, то возникнет переполнение. Если сократить отрезок решения в 10 раз, то выходные данные покажут критический рост нормы 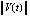 , означающий неустойчивость, при этом данные в строках не будут соответствовать признакам устойчивости. Такое поведение систем вида (37) характерно, в случае асимптотической устойчивости выходные данные программ соответствуют всем предложенным признакам. В случае неасимптотической устойчивости иначе, однако на устойчивость всегда указывает ограниченность нормы по критерию (5), соответствующие примеры приведены в [9]. Неустойчивость системы неизменно идентифицируется по монотонному росту нормы
, означающий неустойчивость, при этом данные в строках не будут соответствовать признакам устойчивости. Такое поведение систем вида (37) характерно, в случае асимптотической устойчивости выходные данные программ соответствуют всем предложенным признакам. В случае неасимптотической устойчивости иначе, однако на устойчивость всегда указывает ограниченность нормы по критерию (5), соответствующие примеры приведены в [9]. Неустойчивость системы неизменно идентифицируется по монотонному росту нормы 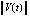 согласно тому же критерию.
согласно тому же критерию.
В целом во всех проведенных численных экспериментах всегда подтверждалась достоверность критериев (5), (6), эквивалентных интегральной форме критериев (7), (8), остальные критерии, в зависимости от конкретной задачи, численно либо согласовались с ними, либо не оказывались с ними в противоречии.
Заключение
Изложен компьютерно-ориентированный метод анализа устойчивости решения системы ОДУ по сочетаниям знаков компонентов решения и их производных. Сформулированы необходимые и достаточные условия устойчивости в инвариантной форме, представлено их математическое обоснование. Выполнена алгоритмизация и инвариантная компьютерная реализация метода на основе приближенного решения системы. Представлен численный эксперимент, даны коды программ, описаны результаты их работы. Данные численного моделирования подтверждают предложенные аналитические условия устойчивости.
Библиографическая ссылка
Ромм Я.Е. КОМПЬЮТЕРНО-ОРИЕНТИРОВАННЫЙ АНАЛИЗ УСТОЙЧИВОСТИ ПО ЗНАКАМ КОМПОНЕНТОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ СИСТЕМЫ И ИХ ДВУХ ПРОИЗВОДНЫХ // Современные наукоемкие технологии. 2021. № 9. С. 100-124;URL: https://top-technologies.ru/ru/article/view?id=38823 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/snt.38823



