Для исследования процесса взаимодействия рабочих органов и почвенной среды сейчас используется комплекс различных методов. Среди них можно выделить две группы – математические методы и экспериментальные лабораторные и полевые исследования (рис. 1). Среди математических методов можно также выделить классическую почвенную механику и численные методы. В свою очередь, экспериментальные исследования разделяются на масштабируемые исследования и полномасштабные [1].
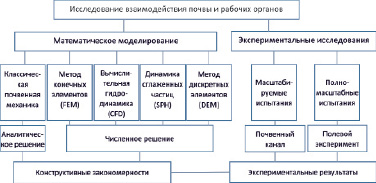
Рис. 1. Различные методы исследования взаимодействия рабочих органов почвообрабатывающих машин и почвенных сред
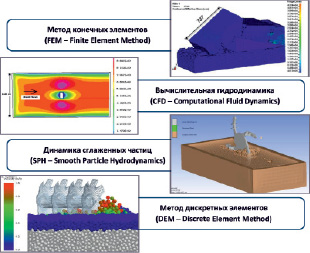
Рис. 2. Применение численных методов для исследования взаимодействия рабочих органов почвообрабатывающих машин и почвенных сред
Целью исследования является изучение возможностей применения численных методов для моделирования взаимодействия почвенной среды и рабочих органов почвообрабатывающих машин.
Материалы и методы исследования
Развитие вычислительных мощностей компьютерной техники и систем автоматизированного проектирования позволило достоверно воспроизводить трехмерную геометрию почвообрабатывающих рабочих органов. Это открыло возможности для преодоления недостатков аналитических и эмпирических методов исследования почвенных взаимодействий за счет применения методов численного моделирования [2]. Основные методы численного моделирования представлены на рис. 2. Среди численных методов можно выделить две большие группы – континуальные и дискретные.
Метод конечных элементов FEM (Finite Element Method) является континуальным методом и заключается в разбиении на конечное количество элементов области, в которой ищется решение дифференциальных уравнений. Наиболее известные программы для расчетов с помощью метода конечных элементов – ANSYS, ABAQUS, NASTRAN, COSMOS/M, LS-DYNA, SOLIDWORKS Simulation.
Вычислительная гидродинамика CFD (Computational Fluid Dynamics) также относится к континуальным методам. Она является подразделом механики сплошных сред, включающим в себя комплекс математических, физических и численных методов, используемых для исследования потоковых процессов. Данный метод реализован в таких программах, как: ANSYS CFX, ANSYS Fluent, FlowVision, Flow Simulation, OpenFOAM.
Хотя имеются преимущества использования континуальных численных методов, предположение о непрерывности почвенной среды далеко не всегда справедливо, так как в процессе обработки происходят разрушение почвенного массива и перемещение образовавшихся агрегатов [2].
Метод дискретных элементов DEM (Discrete Element Method) используется для повышения эффективности процесса моделирования почвенных взаимодействий, что достигается за счет преодоления недостатков непрерывных численных методов. Его применение позволяет описывать не только разрушение и деформацию почвы, но также смещение и примешивание почвенных агрегатов, процессы разуплотнения (уплотнения) почвенной среды и др. Программы, реализующие метод дискретных элементов: EDEM, Rocky DEM, PFC2D and PFC3D, samadii DEM, IVRESS/DIS, Algoryx Momentum Granular, YADE.
Метод динамики частиц (метод молекулярной динамики) обладает схожими возможностями с методом дискретных элементов и заключатся в описании среды как совокупности взаимодействующих частиц (материальных точек или твердых тел). Программы, используемые для расчетов с применением данного метода: AMBER, CHARMM, GROMACS, GROMOS, NAMD [3].
Метод динамики сглаженных частиц SPH (Smooth Particle Hydrodynamics) также используется для моделирования взаимодействия рабочих органов с почвенной средой. В данном методе среда представляется как совокупность дискретных элементов, называемых дискретными частицами. Они имеют пространственное расстояние, называемое длиной сглаживания. Программы, реализующие метод динамики сглаженных частиц: ANSYS Autodyn, Fluids, SPHysics, Pasimodo.
Результаты исследования и их обсуждение
Рассмотрим более подробно исследования по взаимодействию почвенной среды и рабочих органов, выполненные с применением рассмотренных численных методов.
В исследовании [4] приводятся данные об использовании метода дискретных элементов (FEM) для изучения взаимодействия с почвой двугранного клина и лемешно-отвальной поверхности плуга. Моделирование осуществлялось с применением программы LS-DYNA (рис. 3). Для описания поведения почвы была выбрана модель Друкера–Прагера (Drucker–Prager, тип 193). Параметры почвы: плотность 1400 кг/м3; модуль упругости 17 МПа; коэффициент Пуассона 0,25; угол трения 25 °; угол дилатансии 38 °.
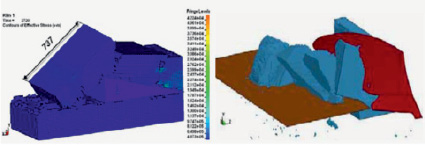
Рис. 3. Моделирование взаимодействия с почвой клина и лемешного плуга методом конечных элементов (FEM)
Использованные в исследовании численные модели, описывающие взаимодействие рабочих органов с почвенной средой, могут достаточно успешно применяться для описания процессов почвообработки. Они позволяют оценить напряжения и деформации, возникающие в почвенном пласте, а также характер их распределения. При этом в исследовании не были изучены такие важные силовые характеристики процесса обработки почвы, как тяговое сопротивление и пространственное распределение его компонентов.
В исследовании [5] также применялся метод конечных элементов (FEM). Было выполнено имитационное моделирование процесса обработки почвы лемешным плугом с использованием средств программы Abaqus (рис. 4). Для имитации почвенной среды была применена эластопластическая модель Мора–Кулона (Mohr–Coulomb) со следующим комплексом параметров: плотность 2000 кг/м3, коэффициент Пуассона 0,3, модуль Юнга 4,106 Н/мм2, пластическая деформация 160 Н/мм2.
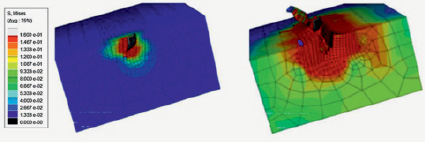
Рис. 4. Моделирование взаимодействия с почвой лемешного плуга методом конечных элементов (FEM)
На первой стадии исследования была создана лемешно-отвальная поверхность плуга в среде САПР SolidWorks. Далее выполнялся экспорт полученной геометрии в программу Abaqus. Опорная точка устанавливалась на кончике отвала, и в ней определялись три пространственных компонента силы реакции. В процессе эксперимента исследовалось влияние угла установки лемеха к стенке борозды и угла установки лемеха к дну борозды на тяговое сопротивление, боковую и вертикальную силы.
Анализ полученных в результате виртуального эксперимента силовых характеристик и их сравнение с данными других исследований позволили подтвердить их достаточно высокую достоверность. При этом на приведенных рисунках видно, что форма поперечного профиля борозды не соответствует получаемой в действительности, а это делает невозможной оценку множества важных характеристик процесса обработки почвы.
В исследованиях [6] был применен метод вычислительной гидродинамики (CFD) для исследования параметров взаимодействия культиваторной стрельчатой лапы с почвой. Для создания имитационной модели использовалась программа ANSYS CFX (рис. 5). Почва моделировалась с применением пластической модели Бингхема (Bingham plastic).
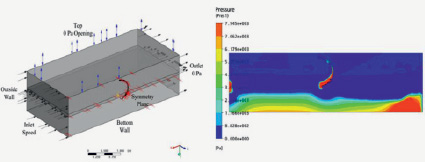
Рис. 5. Моделирование взаимодействия с почвой стрельчатой лапы методом вычислительной гидродинамики (CFD)
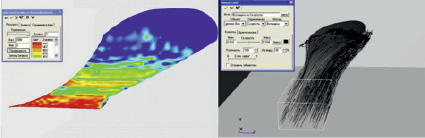
Рис. 6. Моделирование взаимодействия с почвой лемешного плуга методом вычислительной гидродинамики (CFD)
Для проверки данных, полученных в результате моделирования, проводилось сравнение с экспериментальными испытаниями аналогичных стрельчатых лап. При виртуальном моделировании контролировались следующие параметры: давление в различных точках стрельчатой лапы, ширина и глубина обработки, продольная и вертикальная составляющие тягового сопротивления. Определение свойств виртуальной почвы проводилось простым перебором параметров до получения сил сопротивления, схожих с силами, полученными экспериментальным путем.
В результате сравнения данных моделирования с экспериментальными данными было установлено, что продольная составляющая тягового сопротивления, полученная в процессе моделирования, имела значительные ошибки. В проведенной серии пять экспериментов имели расхождение с экспериментальными данными менее 100 %, а один – более 200 %. Также в одном эксперименте наблюдалось снижение тягового сопротивления с ростом ширины захвата стрельчатой лапы, что противоречит существующим данным.
Вертикальная составляющая тягового сопротивления также имела значительные расхождения с экспериментальными данными. Только в двух экспериментах расхождения составили менее 100 %, при этом в трех расхождения были более 200 %. Отклонения от экспериментальных данных в положительную и отрицательную сторону возникали с равной вероятностью.
В исследованиях [7] также был использован метод вычислительной гидродинамики (CFD). Выполнялось моделирование взаимодействия лемешного плуга с почвенной средой. Виртуальный эксперимент реализовывался в программном обеспечении FlowVision (рис. 6). При моделировании в качестве математической модели использовалась модель «Свободная поверхность».
По результатам виртуальных экспериментов установлено, что закономерности взаимодействия корпуса плуга с почвенной средой в зависимости от ее плотности не противоречат значениям, полученным экспериментальным путем. Это позволило задавать плотность среды при моделировании, равной плотности реальных почв.
Наименьшие различия данных тягового сопротивления, полученных при моделировании и экспериментальным путем в почвенном канале, были при вязкости среды в пределах 1000–1300 Па∙с и влажности реальной почвы 16–25 %, составляя не более 5 %. Скорость обработки также значительно влияла на компоненты тягового сопротивления корпуса плуга.
Таким образом, с применением методов вычислительной гидродинамики, описывающих почву как сплошную деформируемую среду, можно эффективно проводить силовой анализ рабочих органов почвообрабатывающих машин. При этом выполнить оценку комплекса качественных параметров обработки почвы (например, формы поперечного профиля, степени разрыхления или уплотнения почвы, характера перемешивания почвенных слоев и др.) с применением данного метода крайне сложно.
В исследовании [8] изучался процесс взаимодействия почвенной среды и различных почвообрабатывающих рабочих органов (стрельчатой лапы и ротационного рыхлителя) с применением метода динамики сглаженных частиц (SPH). Виртуальное моделирование осуществлялось в среде программы ANSYS AUTODYN (рис. 7). Взаимодействие рабочих органов с почвенной средой производилось с применением модифицированной модели Друкера–Прагера (modified Drucker–Prager model).
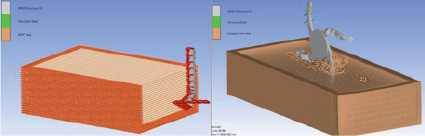
Рис. 7. Моделирование взаимодействия стрельчатой лапы и ротационного рыхлителя с почвой методом динамики сглаженных частиц (SPH)
Данные тягового сопротивления, полученные в результате виртуального моделирования, сравнивались с определенными аналитическим методом данными испытаний в почвенном канале и результатами исследований, выполненных методом дискретных элементов. Результаты SPH-моделирования имели на 5–10 % меньшую точность, чем данные, полученные при DEM-моделировании, но при этом потребовалось значительно меньшее количество вычислительных ресурсов и времени. Тем не менее, по мнению авторов, применение SPH-методов всегда более трудоемко относительно экспериментальных методов. Для устранения данного недостатка потребуется более точная отладка модели взаимодействия.
В исследовании [9] данные по обработке почвы, полученные с использованием FEM-моделирования (рис. 8, а), а также путем экспериментальных исследований (рис. 8, б), были проверены с применением DEM-методов (рис. 8, в), реализованных в программном обеспечении EDEM.
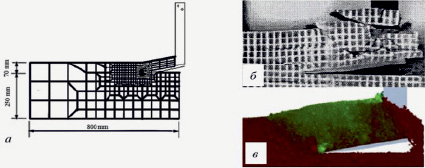
Рис. 8. Моделирование взаимодействия с почвой клина: а – методом конечных элементов (FEM); б – в процессе лабораторных исследований; в – методом дискретных элементов (DEM)
При DEM-моделировании использовалась модель линейной когезии с пружиной с гистерезисом. В исследовании генерировались различные по размерам частицы общим количеством не более 250 000 шт. Наименьший диаметр частицы составлял 3 мм. Полученный в итоге почвенный пласт содержал 221 313 частиц. Применение частиц различных размеров обеспечило достижение достоверной объемной плотности грунта.
При сравнительной визуальной оценке процесса взаимодействия клина с почвенной средой было установлено, что в процессе DEM-моделирования отсутствовало образование трещин, хорошо видное на фотографиях, полученных при испытании аналогичного клина в почвенном канале со стеклянной стенкой. Данный факт объясняется тем, что при DEM-моделировании были использованы дискретные частицы значительно большего размера, чем частицы в почвенном канале. Поэтому, если трещины и образовывались, то были не видны из-за того, что их размер был меньше размера дискретных частиц.
Результаты данного исследования показали, что наиболее достоверные значения тягового сопротивления и вертикальной силы были получены с использованием метода дискретных элементов. Возникшие различия с экспериментальными данными объясняются большим размером частиц, используемых в DEM-моделировании. По мнению авторов, для улучшения точности результатов в будущих исследованиях необходимо сосредоточиться на создании почвенной среды, более близкой по структурному составу к реальным почвам. Следует не только использовать частицы, близкие по размерам к реальным, но и применить частицы с формой, отличной от сферической, которая представляет собой различные комбинации базовых частиц.
В исследовании [10] была разработана математическая имитационная модель, построенная с применением метода дискретных элементов (DEM) (рис. 9). Использование модели дает возможность выполнять комплексные исследования различных рабочих органов почвообрабатывающих машин. В процессе моделирования оценивалось влияние пространственной геометрии почвообрабатывающих рабочих органов, основных технологических параметров рабочего процесса и характеристик почвы на показатели смещения почвы, самоустановки рабочих органов, силовых нагрузок на них, показатели качества рыхления и пространственное распределение показателей. В общей сложности возможно оценить 22 показателя.
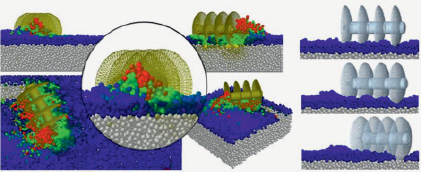
Рис. 9. Моделирование взаимодействия секции дискового культиватора с почвой методом дискретных элементов (DEM)
В работе исследуется один тип рабочего органа – дисковая культиваторная батарея. Оценка адекватности результатов, полученных в процессе моделирования, проводилась путем их сравнения с данными лабораторных исследований. Для этого использовались динамометрическая установка для пространственного тензометрирования и полноразмерная дисковая батарея с геометрическими параметрами, полностью идентичными параметрам 3d-модели, использованной в процессе моделирования. Сравнение производилось по трем компонентам вектора тягового сопротивления. Полученные данные подтвердили схожесть результатов моделирования и данных, полученных в процессе лабораторного эксперимента. Максимальные различия не превышали 22,2 %.
Таким образом, описанные в исследовании математическая модель и программные средства ее реализации дают возможность выполнять комплексную оценку 22 количественных и качественных показателей обработки почвы, а также получать некоторые показатели, оцениваемые ранее лишь на основании данных натурных экспериментов.
Заключение
Анализ существующих исследований в области изучения взаимодействия почвообрабатывающих рабочих органов и почвенных сред показал, что сейчас с разной степенью успешности используется целый ряд численных методов для изучения силовых и технологических характеристик процесса обработки почвы.
FEM-методы могут эффективно применяться для исследования силовых характеристик процесса обработки связных почв. CFD-методы также могут быть использованы для изучения силовых характеристик процесса обработки почв, однако при их применении сложно оценивать качественные показатели обработки почвы. Анализ существующих исследований показал, что на данный момент для разностороннего изучения взаимодействия рабочих органов с почвенными средами наиболее подходящими являются DEM-методы. Их применение позволяет не только оценить силовые параметры процесса обработки почвы, но и исследовать комплекс качественных параметров, без которых результаты моделирования будут неполными. Проведенная экспериментальная проверка результатов моделирования подтверждает их достаточно высокую достоверность.
Библиографическая ссылка
Лысыч М.Н., Шабанов М.Л., Нагайцев В.М., Чернышов В.В. ОБЗОР МЕТОДОВ МОДЕЛИРОВАНИЯ ВЗАИМОДЕЙСТВИЯ РАБОЧИХ ОРГАНОВ ПОЧВООБРАБАТЫВАЮЩИХ МАШИН И ПОЧВЕННЫХ СРЕД // Современные наукоемкие технологии. 2021. № 9. С. 86-93;URL: https://top-technologies.ru/ru/article/view?id=38821 (дата обращения: 01.02.2026).
DOI: https://doi.org/10.17513/snt.38821



