Очевидно, что для вновь вводимых в эксплуатацию движительных комплексов, для которых информация по эксплуатации может на практике ограничиваться одними лишь математическими моделями и расчетами, задача оптимизации управления в условиях неопределенных периодических внешних возмущений становится слабо поддающейся решению. В этом случае целесообразно вводить в эксплуатацию объект управления с возможностью обучения корректирующих устройств, а также накопления массива эксплуатационной информации, что также может быть затруднено ввиду повышенных требований к компетенции обслуживающего персонала, необходимости регулярного прохождения судном маршрутов с разнообразными условиями движения, нежеланием заказчика получать в распоряжение «незаконченный» продукт, обладающий рядом технических ограничений. Опыт западных проектировщиков малооборотных двигателей позволяет судить об определенной абстрагированности от этого вопроса ввиду нечастой необходимости в корректировке регулирующих воздействий при движении в штормовых условиях. Однако для территории России с ее протяженным морским побережьем и суровым северным климатом вопрос оптимизации управления движительными установками крупнотоннажных морских судов стоит достаточно определенно.
В связи с этим авторами была сформулирована цель исследования – рассмотреть и проанализировать возможность использования нейросетевой структуры вместе с нечетким регулятором для повышения эффективности управления судовым главным малооборотным двигателем в штормовых условиях.
Материалы и методы исследования
Концепция предлагаемого авторами алгоритма заключается в параллельной работе объекта управления и математической модели объекта в штормовых условиях. Регулирующее воздействие рассчитывается перманентно как для реального объекта, так и для модели. На вход нейронной сети также поступает непрерывный аналоговый сигнал, однако он подвергается дискретизации, так как конфигурация сети подразумевает подачу на вход сети вектор-столбца входных значений. Таким образом, непрерывное аналоговое значение действительной регулируемой величины поступает на вход дискретизатора, разбивающего ее на итерации посредством блоков задержки и инвертирует вектор-столбец в обратном направлении. Каждую итерацию вектор-столбец обновляется в соответствии с текущим значением частоты вращения коленчатого вала. Выходом нейронной сети служит непрерывное значение определенной частоты синусоидального возмущения, которое подвергается дополнительной фильтрации.
Общий вид модели показан на рис. 1. В состав модели входит реальный объект управления («СМОД»); математическая модель объекта управления, рассчитываемая перманентно параллельно процессу управления объектом («ММ СМОД»), искусственная нейронная сеть для расчета частоты синусоидального воздействия («ИНС»); ограничитель, а также определитель среднего значения частоты воздействия (блоки «Дискретизатор» и «Фильтр»). Кроме того, в состав модели входит нечеткий регулятор для определения значения необходимой задержки времени для корректировки значения регулирующего воздействия регулятора («НР»). В дополнение функцию подачи воздействия реализуют блоки «Переключатель», «Источник синусоидальной нагрузки», «Генератор синусоидального сигнала», «Часы» и прочие.
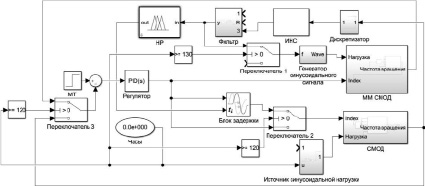
Рис. 1. Структурная схема системы управления частотой вращения СМОД с интегрированным нейросетевым корректирующим контуром обратной связи
Рассмотрим интеграцию предлагаемой концепции для случая частоты вращения коленчатого вала главного двигателя, равной 75 об/мин и соответствующей навигационному полному ходу, а также последующему появлению синусоидального возмущения через 40 с после начала моделирования процесса. В начальный момент времени заданное значение частоты вращения поступает с машинного тел («МТ») на элемент сравнения, где определяется текущая ошибка регулирования. Далее ошибка регулирования поступает на вход регулятора, где определяется регулирующее воздействие в соответствии с ПИД-законом управления [2]. Рассчитанное регулирующее воздействие в виде электрического сигнала поступает на усилитель и далее в контур подготовки подачи топлива, где посредством расчета выходных воздействий передаточных функций определяется расход топлива каждого из шести цилиндров Gц.
Определенное значение поступает на вход модели судового главного малооборотного двигателя, выходным значением которой является значение регулируемой величины – частоты вращения Xт. Одновременно с реализацией функции обратной связи текущее значение регулируемой величины поступает на формирователь входного значения искусственной нейронной сети «Дискретизатор». Данный модуль необходим в связи с использованием искусственной нейронной сети и необходимостью сведения аналогового входного значения, изменяющегося в пределах [-60; 0] (для полного заднего хода) и [0; 80] (для полного переднего хода) к значениям [-4; 4] – амплитудным величинам массива входных воздействий ИНС. В задачу модуля входит математическое преобразование синусоидальных входных значений одной амплитуды в значения другой амплитуды, но той же частоты.
Преобразованное значение регулируемой величины поступает в модуль определения частоты синусоидального сигнала на основе искусственной нейронной сети. Предварительное преобразование непрерывного аналогового сигнала в блоке дискретизации при работе на том же режиме имеет вид (рис. 2).
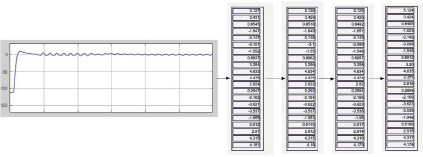
Рис. 2. Предварительное преобразование непрерывного аналогового сигнала в блоке дискретизации
Последующая обработка вектор-столбца возлагается на разработанную структуру ИНС [1]. Нейронная сеть формирует непрерывный сигнал диапазона [0.05; 0.145] Гц, соответствующий частоте входного сигнала частоты вращения коленчатого вала. Однако в данной конфигурации становится неизбежным возникновение помех и шумов, особенно при возникновении переходных процессов, что неизбежно сказывается на точности работы ИНС и качестве управления процессом. По этой причине на этапе разработки в состав модели был включен модуль отбора выборки («Фильтр») на интервале времени c t1 = 70 по t2 = 100 c, отсекающий все значения регулируемой величины в переходном процессе и после значения t2. Необходимое в данном случае определение среднего значения за период времени t1...t2 реализуется блоком определения среднего, входящего в блок «Фильтр».
Блок реализует задачу поиска среднего в соответствии с передаточной функцией [3]:
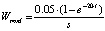 .
.
Полученное окончательное значение частоты синусоидального воздействия поступает на вход нечеткого регулятора для расчета значения времени задержки подачи регулирующего воздействия на вход объекта.
Так как задача поддержания заданного значения частоты вращения главного двигателя возлагается на ПИД-регулятор, то задачу нечеткого регулятора следует обозначить как реализацию корректирующего воздействия, а весь контур в составе искусственной нейронной сети и нечеткого регулятора – нейросетевым корректирующим звеном (НКЗ) обратной связи.
Рассматривая работу НКЗ с нечетким регулятором применительно к данной системе, следует сделать ряд определенных замечаний: для оптимальной работы нечеткого регулятора на его вход должно поступать непрерывное значение частоты возмущающего воздействия. Нечеткое множество A, соответствующее множеству кортежей <x, μA(x)>, где x – элемент универсума (в данном случае – элемент множества [0.05; 0.145]), а μA(x) – функция принадлежности, ставящая элементу xi, принимающая значение в пределах [0; 1], определяет весь массив входной информации, необходимой для корректной работы нечеткого регулятора [4].
В итоге поступающий на вход НР массив информации порождает на множестве всех десятичных цифр X = {0,1,2,3,4,5,6,7,8,9} конечное нечеткое множество A (частота воздействия 0.05 Гц) = {<0.05, 1>, <0.1, 0.8>, <0.15, 0.2>, <0.2, 0>, <0.25, 0>, <0.3, 0>, <0.35, 0>…}. На основе данного множества строится график функции принадлежности нечеткого множества «частота воздействия 0.05 Гц».
Классическая интерпретация процесса нечеткого вывода содержит несколько основных этапов (рис. 3) [5, 6]. Рассматриваемый алгоритм может быть реализован неоднозначным способом. В данном исследовании авторами была предпринята попытка использования алгоритма Сугено.
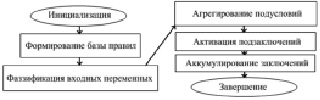
Рис. 3. Алгоритм классической интерпретации нейронечеткого вывода
Тогда кусочно-линейные, а также Z-образные функции принадлежности можно представить в виде
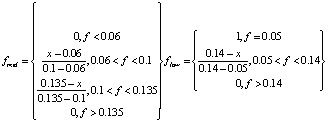
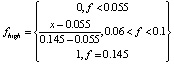
Аналогично классическим продукционным системам важным компонентом нечетких систем является метод вывода заключений на базе правил нечетких продукций. Среди методов различают прямой и обратный. Первый (fuzzy forward-chaining reasoning) подразумевает замену классической импликации A϶B (где A и B – некоторые посылки правила) на правило: «ЕСЛИ x есть A, то y есть B», где A и B есть нечеткие множества, а само правило нечеткой продукции представляет некоторое нечеткое отношение между переменными x и у. Для данного метода (Сугено) этап формирования базы правил отличается использованием только правил в форме [6]:
ПРАВИЛО #n: ЕСЛИ «β1 есть α» И «β2 есть α», ТО «ω = ε1∙a1 + ε2∙a2»,
где ε1 и ε2 – есть действительное число, ω – выходная лингвистическая переменная.
В данном случае количество правил продукций регламентируется количеством нечетких значений входной величины, то есть частоты. В текущей конфигурации оно равно трем. Соответственно, целесообразно сформулировать двадцать правил продукций, представляющих алгоритм корректного определения параметра звена запаздывания.
ПРАВИЛО #1: ЕСЛИ «частота возмущающего воздействия низкая», ТО «параметр звена запаздывания t принимает максимальное значение».
ПРАВИЛО #2: ЕСЛИ «частота возмущающего воздействия средняя», ТО «параметр звена запаздывания t принимает среднее значение».
ПРАВИЛО #3: ЕСЛИ «частота возмущающего воздействия высокая», ТО «параметр звена запаздывания t принимает малое значение».
Фаззификация в данном методе реализуется посредством определения всех входных переменных системы, то есть множества значений V = {a1, a2,…, an}. Далее рассматривается каждое из подусловий правил «β1 есть α». При этом значение α используется в качестве аргумента функции принадлежности μ(x). Тем самым определяется количественное значение μ(x), которое и является результатом фаззификации.
Агрегирование подусловий в методе Сугено реализуется посредством логической операции минимум-конъюнкции. Активизация подзаключений реализуется, во-первых, при помощи метода минимум-активизации [7]:
μ'(y) = min{ci, μ(y)},
где определяется степень истинности всех заключений правил нечетких продукций; во- вторых, осуществляется расчет значений выходных переменных каждого правила. Это достигается посредством использования формулы для определения заключения, только кроме переменных α1 и α2 подставляются значения входных переменных. Тем самым определяется множество значений выходных переменных W = {w1, w2,…, wn}.
Аккумуляция заключений нечетких правил продукций фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами.
Для дефаззификации выходных переменных используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств, а именно [8]:
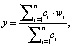
где n – общее количество активных правил, в подзаключениях которых присутствует выходная лингвистическая переменная wi.
В данном случае роль объекта управления играет звено подготовки топлива и главный двигатель. Роль датчика обратной связи – искусственная нейронная сеть для определения частоты синусоидального воздействия. Содержательная постановка задачи сводится к определению спектра значений параметра t, описывающего «Блок задержки» (рис. 1).
Исследуемый регулятор строится в редакторе систем нечеткого вывода FIS [9], при этом тип системы нечеткого вывода определяется как тип Сугено, метод логической конъюнкции – метод алгебраического произведения, метод логической дизъюнкции – метод алгебраической суммы, метод вывода заключения – метод минимального значения, метод агрегирования – метод максимального значения, метод дефаззификации – метод взвешенного среднего.
Этап дефаззификации считается законченным, когда для каждой из выходных логистических переменных (малое/среднее/высокое значение времени задержки) будут определены итоговые количественные значения в форме некоторого вещественного числа, то есть: tlow = 4,5 с, tmid = 9,25 с, thigh = 14 с.
Полученная нечеткая структура способна корректировать параметр задержки звена запаздывания с целью компенсации синусоидального возмущения судового главного двигателя. Возможности полученной структуры можно продемонстрировать на примере поступающей на вход нечеткого регулятора кривой (рис. 4).

Рис. 4. Вход-выходная характеристика разработанного нечеткого регулятора
Результаты исследования и их обсуждение
Разработанная структура способна выполнять поставленные задачи с заданной степенью точности, позволяя корректировать значение настроечного параметра звена запаздывания в заданных пределах. Реакцией ИНС служит определение частоты непрерывного значения, поступающего на ее вход сигнала; при этом заведомо не поддающиеся анализу значения отфильтровываются и отсекаются. Блок фильтрации позволяет вычислить оптимальный участок работы ИНС, по всему спектру которого определяется среднее и максимальное значение. Данное значение поступает на вход нечеткого регулятора и одновременно на формирователь синусоидального сигнала для модели главного двигателя («Генератор синусоидального сигнала» на рис. 1), выходной сигнал которого поступает на вход модели главного двигателя («ММ СМОД» на рис. 1), выходное значение которой поступает на вход основного регулятора, формирующего регулирующее воздействие, однако оно подается не напрямую на усилитель и объект управления, а через звено запаздывания, настроечный параметр которого регламентируется результатом работы нечеткого регулятора, определяющего эту величину при помощи входного сигнала частоты воздействия. При работе на частоте вращения 75 об/мин при синусоидальной нагрузке частотой 0,1 Гц блок выполняет преобразование (рис. 5).
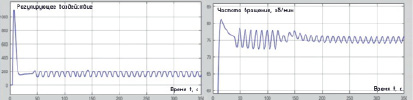
Рис. 5. Форма переходного процесса при работе СМОД на частоте вращения 75 об/мин и при синусоидальной нагрузке частотой 0.1 Гц, компенсируемой разработанной структурой
Здесь переходной процесс инициализируется изменением заданного значения частоты вращения с 0 до 75 об/мин. После выхода объекта на заданный режим работы в момент времени t = 40 с изменяется нагрузка объекта управления. Симулируется движение судна при наличии штормовых условий плавания. Достигается это путем появления синусоидальной составляющей вида
S = 100∙sin(2∙π∙f∙t)
на входе передаточной функции по нагрузке объекта управления.
Заключение
После появления устойчивых по амплитуде и частоте колебаний регулируемой величины в пределах 72,2–77,8 об/мин в момент времени t = 120 с происходит переключение управления с управления по реакции объекта на управление по реакции модели. При этом в этот же момент времени значение измеренной частоты синусоидального возмущения подается на блок моделирования возмущения, а затем полученный сигнал – также на вход математической модели главного двигателя, заставляя значение моделируемой регулируемой величины изменяться по некоторой закономерности.
Полезным результатом данного алгоритма служит значительное снижение амплитуды колебаний регулируемой величины (рис. 5), что крайне положительно сказывается на увеличении ресурса цилиндро-поршневой группы, агрегатов и соответствующих финансовых затратах.
Библиографическая ссылка
Куколев А.А., Пиотровский Д.Л., Подгорный С.А. МЕТОД УПРАВЛЕНИЯ ЧАСТОТОЙ ВРАЩЕНИЯ СУДОВОГО ГЛАВНОГО МАЛООБОРОТНОГО ДВИГАТЕЛЯ В ШТОРМОВЫХ УСЛОВИЯХ // Современные наукоемкие технологии. 2021. № 8. С. 101-106;URL: https://top-technologies.ru/ru/article/view?id=38786 (дата обращения: 09.03.2026).
DOI: https://doi.org/10.17513/snt.38786



