Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Киренберг А.Г. 1 Кисляков И.М. 2 Медведев А.В. 1, 3 Прокопенко Е.В. 1

---

1 ФГБОУ ВО «Кузбасский государственный технический университет им. Т.Ф. Горбачева»

2 Кемеровский институт (филиал) Российского экономического университета имени Г.В. Плеханова

3 Кемеровский государственный университет

Статья посвящена описанию постановки задачи и построению математической модели оценки экономической эффективности территориально-производственного кластера как сложной социально-экономической системы. Рассмотрены некоторые модельные подходы к решению указанной задачи, проведен их краткий анализ. Математическая модель кластера строится на основе оптимизационного подхода и является многокритериальной задачей линейного программирования, основной идеей применения которой представляется выявление экономического потенциала кластера. Знание максимальных инвестиционно-производственных возможностей кластерной структуры позволит принимать управленческие решения, мотивирующие экономических агентов к участию в кластере, задействовать рыночные механизмы внедрения инноваций в конкретные производственные отрасли или направления экономической деятельности территорий, а также сориентирует на выявление оптимальных объемов и пропорций осуществляемых ими инвестиционных, производственных и финансовых затрат с учетом маркетинговых, трансакционных, инновационных, инфраструктурных, экологических, финансовых и других аспектов функционирования кластера. В работе обосновано существование решения задачи, соответствующей представленной математической модели, что позволяет использовать эффективные численные методы ее анализа и разрабатывать системы поддержки принятия инвестиционных, производственных и финансовых решений относительно выбора оптимальных объемов инвестиций, производства продукции предприятиями кластера, способов финансирования его деятельности.

Статья в формате PDF

311 KB

территориально-производственный кластер

инновации

оптимизационный подход

многокритериальная задача линейного программирования

система поддержки принятия решений

1. Макаров В.Л., Бахтизин А.Р., Сушко Е.Д. Агент-ориентированная социо-эколого-экономическая модель региона // Национальные интересы: приоритеты и безопасность. 2015. Т. 11. № 3 (288). С. 2–11.

2. Porter M.E. Cluster Mapping Project, Institute for Strategy and Competitiveness, Harvard Business School. [Electronic resource]. URL: http://www.isc.hbs.edu/econ-clusters.htm (date of access: 15.05.2021).

3. Буянова М.Э., Дмитриева Л.В. Оценка эффективности создания региональных инновационных кластеров // Вестник Волгоградского государственного университета. Серия 3: Экономика. Экология. 2012. № 2 (21). С. 54–62.

4. Боуш Г.Д., Куликова О.М., Шелков И.К. Агентное моделирование процессов кластерообразования в региональных экономических системах // Экономика региона. 2016. Т. 12. Вып. 1. С. 64–77.

5. Машунин Ю.К., Машунин К.Ю. Стратегическое и инновационное развитие кластера на базе цифровой экономики // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Экономические науки. 2018. Т. 11. № 4. С. 85–99.

6. Медведев А.В. Автоматизированная поддержка принятия оптимальных решений в инвестиционно-производственных проектах развития социально-экономических систем. М.: Издательский Дом «Академия Естествознания», 2020. 200 с. DOI: 10.17513/np.421.

7. Медведев А.В., Кисляков И.М. Автоматизированный расчет экологических платежей при взаимодействии предприятий угольной отрасли с региональным управляющим центром / Вестник научного центра ВостНИИ по промышленной и экологической безопасности. 2017. № 3. С. 54–61.

8. Штойер P. Многокритериальная оптимизация: теория, вычисления, приложения. М.: Наука, 1982. 600 с.

9. Данциг Дж. Линейное программирование, его обобщение и применение. М.: Прогресс, 1966. 600 с.

10. Медведев А.В. Цифровые двойники территорий для поддержки принятия решений в сфере регионального социально-экономического развития // Современные наукоемкие технологии. 2020. № 6–1. С. 61–66. DOI: 10.17513/snt.38072.

Проблема экономико-математического моделирования деятельности и оценки экономической эффективности территориально-производственных кластеров (ТПК) остается весьма актуальной [1, 2], прежде всего в связи с использованием моделей ТПК для решения задач планирования и прогнозирования социально-экономического развития регионов. Математические модели ТПК базируются преимущественно на имитационном подходе, использующем методы анализа инвестиционных, производственных и финансовых потоков, циркуляция и динамика которых математически описывается дифференциальными уравнениями первого порядка. Не менее популярными остаются регрессионно-статистический [3] и экспертный [4] подходы, позволяющие строить и оценивать эффективность ТПК через регрессионные уравнения связи факторов с учетом их экспертных оценок. В работе [5] рассмотрена оптимизационная линейная модель кластера с заданным частным набором коэффициентов удельных ресурсных затрат в экономической системе. В данной работе рассматривается подход к анализу ТПК, включающий линейную оптимизационную модель его развития, ориентированную на использование описанного в [6] автоматизированного комплекса многопараметрического анализа указанной модели, представляющих соответствующую систему поддержки принятия решений с учетом эколого-экономического комплекса [7] проблем угледобывающей территории.

Материалы и методы исследования

Рассмотрим следующую содержательную постановку задачи, описывающую деятельность ТПК. Пусть на некоторой экономической территории функционирует совокупность организаций, объединенная в ТПК, связанная с производством и реализацией n видов продукции (товаров и/или услуг). Для производства каждого вида продукции используется комплект основных производственных фондов (комплект ОПФ), имеющий следующие характеристики: сk – рыночная стоимость k-го комплекта ОПФ (денежных единиц, д.е.); Vk – производительность k-го комплекта ОПФ (количество единиц продукции, производимой данным комплектом; ед.прод/комплект ОПФ); Tk – срок полезного использования k-го комплекта ОПФ (экономических циклов, э.ц.). Предполагается, что стоимость комплектов ОПФ включает стоимости всех составляющих его материальных и нематериальных активов, без которых невозможны производство и реализация соответствующей продукции. Иначе говоря, в ОПФ осуществлены соответствующие капиталовложения (инвестиции). Производимая на указанных комплектах ОПФ (в соответствии с принципом чистых отраслей) продукция n видов имеет различную рыночную цену Pk единицы k-го вида и различный стоимостной спрос qk на продукцию k-го вида, определяемый на территории долей рынка, занимаемой производимой продукцией. Производство k-го вида продукции характеризуется своими условиями (трудо- βk и материалоемкостью pk, как экспертно задаваемыми долями общепроизводственных затрат на производство продукции), а также своими управленческим и рыночным окружением (системой управления, условиями финансирования, уровнем инфляции, горизонтом планирования и пр.). Для удобства проект производства некоторого вида продукции в кластере далее будем также называть проектом кластера. Введем следующие обозначения: 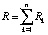, 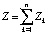– соответственно суммарные общие доходы и расходы предприятий кластера, где Rk, Zk – соответственно доходы и расходы предприятий, производящих k-й вид продукции; Z = Amk + Fk + N1k + N2k + N4k + N5k + zk – общие расходы в кластере; где Amk – амортизация ОПФ предприятий кластера, производящих k-й вид продукции; Fk – фонд оплаты труда (ФОТ) на предприятиях кластера, производящих k-й вид продукции; N1k – налог на добавленную стоимость (НДС) предприятий кластера, производящих k-й вид продукции; N2k – налог на имущество (НИ) предприятий кластера, производящих k-й вид продукции; N3 – налог на прибыль (НП) предприятий кластера, производящих k-й вид продукции; N4 – страховые взносы в социальные фонды (СВ), предприятий кластера, производящих k-й вид продукции; N5k – дополнительные (страховочные) затраты предприятий кластера, производящих k-й вид продукции (в том числе экологические штрафы, метод учета которых представлен, например, в [7], другие налоговые и неналоговые затратные потоки, пропорциональные объемам производства продукции в материальном или финансовом отношении при функционировании ТПК); αi (i = 1,...,5) – соответствующие средние ставки указанных налоговых и неналоговых затрат; z – суммарные оборотные расходы предприятий кластера; zk – оборотные расходы предприятий кластера, производящих k-й вид продукцию; Wk = (1 – α3)(Rk – Zk) – чистая прибыль предприятий кластера, производящих k-й вид продукции; Sk0 – остаточная стоимость ОПФ предприятий кластера, производящих k-й вид продукции; DSP = DSP0 + W + CrP + DotP – суммарные текущие средства всех предприятий кластера, где DSP0 – начальные средства всех предприятий кластера; CrP – сумма кредитования текущей деятельности кластера; DotP – сумма дотаций (государственное или другое беспроцентное (безвозвратное) финансирование) на функционирование кластера; DSC = DSC0 + ZPC + CrC + DotC – суммарные текущие средства домохозяйств ТПК, где DSС0 – начальные средства домохозяйств ТПК; ZPC – заработная плата домохозяйств от предприятий ТПК; CrC – сумма кредитования домохозяйств, сотрудничающих с организациями ТПК; DotС – сумма дотаций (государственное или другое беспроцентное (безвозвратное) финансирование) домохозяйствам сотрудничающим с организациями ТПК;

–

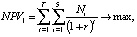
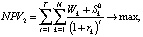
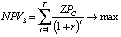критерии эффективности управляющего центра, производителя и потребителя соответственно, где rk – ставки дисконтирования потоков в k-м проекте кластера, учитывающие инфляцию, уровень требований инвестора и другие экономические и политические риски деятельности предприятий кластера; r – ставка инфляции на горизонте T планирования развития ТПК. В таблице представлены классификация введенных параметров по группам, их единицы измерения, а также описаны содержательные ограничения деятельности ТПК, учитываемые в формируемой модели.

Отметим, что большинство приведенных в таблице показателей, характеризующих комплекты ОПФ и продукцию предприятий кластера, особенности ее производства и продажи, ограничения производства и окружающей рыночной среды, могут быть «считаны» при анализе рыночной информации из различных источников (сайты официальной экономической статистики, публикации открытой аналитики, открытая бухгалтерская отчетность предприятий и т.п.). Введем далее следующие обозначения переменных и комплексов: хk – объем инвестиций в ОПФ k-го вида, {д.е.}; хn+k – выручка от продажи продукции k-го вида, {д.е.}; x2n+1 – объем кредита, взятого на финансирование текущей деятельности предприятий кластера, {д.е.}; x2n+2 – объем дотации на финансирование как стратегической, так и тактической деятельности предприятий кластера, {д.е.}. Тогда

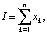
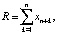
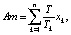
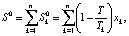
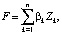
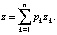
Суммарные производственные затраты состоят из суммарных инвестиционных затрат I и текущих затрат Z, включающих текущие затраты Zk каждого из n предприятий, производящих продукцию ТПК:

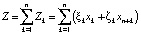, где , ;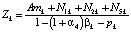

; ; ;

.

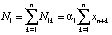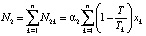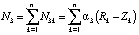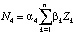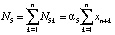Следует отметить, что все содержательные потоки (доходов, расходов, прибыли, инвестиций, собственных средств, остаточной стоимости ОПФ и др.) зависят линейно от искомых переменных задачи xk, xn+k, x2n+1, x2n+2. Поэтому с учетом приведенных обозначений и ограничений, математическая модель ТПК в матричном виде примет форму следующей трехкритериальной задачи линейного программирования:

A(2n+4)× (2n+2) x(2n+2)×1 ≤ b(2n+4)×1, x(2n+2)×1 ≥ 0, NPV1(х) → max, NPV2(х) → max, NPV3(х) → max, (*)

где

,

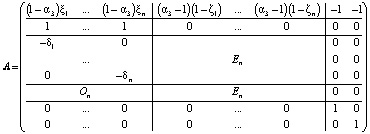b(2n+4)×1 = (DS0; Imax;0,…,0; q1,…,qn; 1Crmax; Dotmax)T,

,

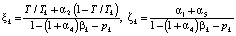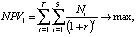
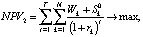
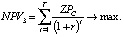
Описание деятельности ТПК в форме (*) позволяет автоматизировать расчеты в соответствующей информационно-аналитической системе, так как модель (*) представляет собой многокритериальную задачу линейного программирования с допустимым множеством в виде непустого компакта, что гарантирует существование решения этой задачи для всех допустимых значений входящих в нее параметров. Кроме того, в силу линейности модели, например, в соответствии с [8], трехкритериальная модель эквивалентна соответствующей однокритериальной с критерием в виде выпуклой линейной комбинации критериев (1):

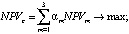
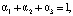
что позволяет автоматизированно получать решение (1) с использованием симплекс-метода Дж. Данцига [9], а также проводить многокритериальный анализ задачи путем анализа соответствующего ей Парето-множества с помощью описанного в [6] программного комплекса и алгоритмов работы [7]. Легко проверяется, что нулевой вектор является частным решением системы (1), а ее нетривиальное решение также получается с использованием указанного программного комплекса. Таким образом, это позволяет рассматривать данную совокупность инструментов (модель – алгоритм – пакет программ), как ориентированную на конечного пользователя – экономиста-аналитика – систему поддержки принятия управленческих решений в сфере функционирования, планирования и прогнозирования развития ТПК.

Результаты исследования и их обсуждение

Построенная математическая модель позволяет получить количественную оценку экономического потенциала ТПК, а также трактовать различные особенности его функционирования – маркетинговые, трансакционные, инновационные, инфраструктурные, экологические, финансовые. Например, учет маркетинговых, трансакционных, экологических издержек возможен в модели путем рассмотрения пропорциональных объемам производства затратных потоков, например в потоке N5 или в ставке дисконтирования. Инновационный характер производимой продукции можно учесть путем рассмотрения следующей цепочки рассуждений. Назовем набор Т(сk,Тk,Vk,Pk,qk,βk,рk) традиционной («старой») технологией производства продукции k-го вида (или соответствующего ей по функционалу аналога инновационной продукции), а набор Т*(сk*,Тk*,Vk*, Pk*, qk*, βk*, рk*), где сk* = γkсk, Тk* = τkТk, Vk* = νkVk, Pk* = πkPk, qk* = σkqk, βk* = φkβk, рk* = ρkpk – инновационной («новой») технологией производства продукции k-го вида продукции. Здесь коэффициенты γk, τk, νk, πk, σk, φk, ρk – экзогенно (в частности, экспертно) задаваемые величины, отражающие соответственно оценки изменения численных значений характеристик активов, продукции, особенностей производства и продажи продукции при переходе к «новой» технологии. Сравнение расчетов по модели (1) с характеристиками, соответствующими технологиям Т и Т*, может помочь выявить влияние на показатели развития кластера производственных, технологических, маркетинговых инноваций путем комбинации коэффициентов γk, τk, νk, πk, σk, φk, ρk. Например, включение в кластер предприятия (группы предприятий) по производству некоторой продукции может повлиять на их доступ к производственным технологиям, государственной поддержке, расширению доли рынка и, соответственно, увеличению спроса на продукцию. Также возможен учет различных инфраструктурных особенностей производства, например, путем включения в состав ТПК соответствующих предприятий, не занимающихся производством профильной продукции. При этом указанные изменения и особенности возможно учесть и оценить (как экспертно, так и путем маркетингового анализа) через варьирование значений параметров γk, τk, νk, πk, σk, ρk. Наличие в ТПК подготовленных квалифицированных кадров для производства продукции кластера или, соответственно, учет необходимых для этого затрат может отражаться в значениях коэффициентов φk. Особенности системы управления в кластере, в том числе учитывающие дивидендную политику крупных предприятий кластера, – через ставки дисконтирования rk и r, особенности финансирования развития кластера – через ставки r и r0 и так далее.

Заключение

Представленная математическая модель ТПК является многокритериальной задачей линейного программирования, имеющей эффективные инструменты ее численного анализа. Аналогичные предложенной оптимизационные математические модели социально-экономических систем различного экономического уровня, учитывающих некоторые из присущих ТПК особенностей его функционирования, рассмотрены в работе [6]. Там же приведены результаты соответствующих расчетов, подтверждающих содержательную адекватность указанных математических моделей. Отметим, что необходимая для оперативного анализа экономической эффективности инвестиционно-производственных проектов развития ТПК скорость расчетов позволяет рассматривать используемый инструментальный комплекс как основу и ключевую составляющую построения социально-экономического цифрового двойника [10] такой сложной социально-экономической системы, как территориально-производственный кластер.

Библиографическая ссылка