Малотоннажная химия занимает важное место в структуре мировой химической индустрии. В странах Евросоюза доля высокотехнологичной малотоннажной химической и нефтехимической продукции составляет 28 % отраслевого выпуска. В РФ доля малотоннажной химии в химическом производстве не превышает 5 %. Это связано с тем, что в постсоветский период развитию малотоннажных химических производств в РФ практически не уделялось внимания. Значительное число предприятий и производств по выпуску малотоннажной химической продукции, созданных в советский период, прекратили свое существование. Как следствие, объем выпуска продукции малотоннажной химии в РФ упал в десятки раз, и основная часть потребностей в этой продукции стала удовлетворяться за счет импорта (по различным группам товаров малотоннажной химии – от 70 до 100 %) [1].
Лакокрасочные материалы (ЛКМ) являются важным видом продукции малотоннажной химии, наиболее близким к реальному рынку товаром и точкой приложения научно-технических усилий по организации и реализации высоких наукоемких технологий. Эти обстоятельства привели к целесообразности введения концепции «пэйнт-технологий», обобщающей наукоемкие технологии производства и нанесения ЛКМ, характеризующие научно-технический прогресс в области окраски различных поверхностей и создания защитных покрытий [2].
В современной экономической ситуации предприятие должно максимально быстро удовлетворять требования конечного потребителя и без значительных затрат переналаживаться на выпуск новой продукции. Для решения данной проблемы представляется перспективным создание гибких многоассортиментных малотоннажных производств ЛКМ, что является одним из приоритетных направлений экономически устойчивого развития лакокрасочной отрасли в РФ.
Цель работы – разработка гибкой производственной системы получения ЛКМ различного назначения с использованием современных технологических разработок, оборудования и методов управления.
Теоретический анализ производства ЛКМ. Комплекс перечисленных задач предлагается решить методами искусственного интеллекта и экспертных систем (ЭС). В объектно-ориентированной экспертной системе обрабатывается как качественная слабо формализуемая, так и количественная информация, в связи с чем экспертная система организуется как интегрированная, состоящая из информационно-логической и расчетной подсистем [3–5]. В частности, функция расчетной подсистемы заключается в реализации структурной и параметрической оптимизации химико-технологических систем (ХТС) производства многономенклатурных лакокрасочных материалов.
Разрабатываемая ЭС предназначена для проектирования аппаратурно-технологических схем производства лакокрасочных материалов широкого ассортимента, создаваемых на основе блочно-модульного оборудования, а также для рекомендаций по размещению новых технологических процессов на оборудовании действующих производств. Экспертная система является интегрированной и содержит наряду с традиционными средствами ЭС, обобщающими и моделирующими опыт технологов и проектантов, эффективные алгоритмы синтеза многопродуктовых систем периодического и полунепрерывного действия со сложной аппаратурной структурой и произвольной дисциплиной выпуска продукции, в том числе организованными в соответствии с блочно-модульным принципом аппаратурного оформления [4–6]. Применение ЭС позволяет осуществить выбор адекватного схемного решения, аппаратурного оформления технологических процессов, оптимизации технологических режимов [4; 7].
В качестве объекта исследования для разработки и создания прототипа интегрированной экспертной системы выбрано производство следующих ЛКМ перспективного ассортимента: пентафталевых и нитроцеллюлозных товарных и полуфабрикатных лаков; меламиноформальдегидных смол; пентафталевых и меламиноформальдегидных эмалей и грунтовок.
В производстве ЛКМ перспективного ассортимента применяется следующее технологическое оборудование: реакторы с индукционным обогревом, якорно-лопастной мешалкой и погружным змеевиком, параметрический ряд которых представлен следующими значениями объема: 1 м3, 2 м3, 3,2 м3, 5 м3, 6,3 м3; смесители с охлаждающей рубашкой и рамной мешалкой, параметрический ряд которых представлен следующими значениями объема: 2 м3, 5 м3, 6,3 м3, 10 м3, 16 м3; горизонтальные кожухотрубчатые теплообменники (одно- и двухходовые) в качестве конденсаторов реакторов и смесителей; патронные фильтры типа «Кюно»; диссольверы для непрерывного или периодического перемешивания; горизонтальные бисерные мельницы с объемом размольного цилиндра 20 и 50 л.
Классификация структурных типов ХТС выполнена по следующим признакам: количество продуктов, временной режим работы технологического оборудования, способ взаимодействия технологических аппаратов, аппаратурная структура технологической системы. Признаки измерены в номинальных шкалах, несочетаемые значения признаков исключены методом морфологического анализа в форме морфологического ящика. В результате для структурной и параметрической оптимизации оставлены следующие структурные типы химико-технологических систем: индивидуальные, многопродуктовые ХТС с последовательной, последовательно-параллельной и параллельно-последовательной структурой (для многопродуктовых ХТС – фиксированной или переменной), содержащие аппараты только периодического или периодического и полунепрерывного действия, взаимодействующие непосредственно или через демпфирующие емкости-накопители [8–11]. Разработаны оптимизирующие модели и простейшие алгоритмы структурной (для систем с переменной структурой) и параметрической оптимизации.
Структурно-функциональная схема интегрированной экспертной системы для автоматизации проектирования производств ЛКМ. Проектирование производства многоассортиментной лакокрасочной продукции осуществляется с помощью объектно-ориентированной интегрированной экспертной системы, содержащей информационно-логическую и расчетную подсистемы. В диалоге с экспертной системой проектант выбирает подходящее технологическое оборудование и тип аппаратурной структуры химико-технологических систем, адекватный продукции проектируемого ассортимента; формирует оптимизирующую математическую модель и выбирает эффективный алгоритм структурной и параметрической оптимизации химико-технологической системы [8–10]. Структурно-функциональная схема интегрированной экспертной системы изображена на рис. 1.
Структурная оптимизация химико-технологических систем. Алгоритмы автоматизированного выбора технологического оборудования. Выбор типа технологического аппарата, адекватного технологическому процессу при отсутствии его математической модели, осуществляется методом экспертных оценок. Нечеткий выбор адекватных типов технологических аппаратов формально равнозначен методу поиска недоминируемых альтернатив. Исходной информацией являются экспертные оценки в форме результатов парных сравнений, имеющих вид матрицы бинарных отношений [12–13]. Разработанные алгоритмы различаются в зависимости от способа задания экспертных оценок. Ниже описаны два алгоритма.
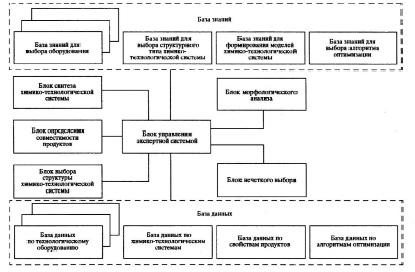
Рис. 1. Структурно-функциональная схема интегрированной экспертной системы
Алгоритм 1. В соответствии с этим алгоритмом типы аппаратов сравниваются попарно по каждому признаку j 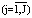 . В результате формируются матрицы бинарных отношений аппаратов по каждому из признаков; количество матриц равно количеству признаков; элементы aik матриц формируются по правилу:
. В результате формируются матрицы бинарных отношений аппаратов по каждому из признаков; количество матриц равно количеству признаков; элементы aik матриц формируются по правилу:
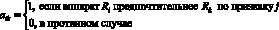 (1)
(1)
В результате экспертной оценки получаются J отношений предпочтения rj на множестве типов аппаратов R. Задача заключается в выборе наиболее подходящего аппарата из множества (R, r1, r2, ..., rJ). Отношения rj выражены в виде некоторых функций fj. Значения функций fj(R) понимают как числовую оценку аппарата R по признаку j. Тогда формально задача выбора адекватного типа аппарата означает выбор аппарата, имеющего возможно большие оценки по всем признакам, то есть выбор производится по следующему правилу:
если fj(r) ³ fj(R0), то fj(r) = fj(R0); 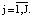
Для нахождения множества эффективных альтернатив вместо отношения rj; 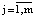 можно взять их пересечение Q1 и найти множество недоминируемых альтернатив в множестве (R, Q1). В свою очередь, пересечение отношений rj можно представить в иной форме, если ввести функцию принадлежности отношений rj:
можно взять их пересечение Q1 и найти множество недоминируемых альтернатив в множестве (R, Q1). В свою очередь, пересечение отношений rj можно представить в иной форме, если ввести функцию принадлежности отношений rj:
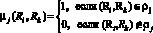 (2)
(2)
Пересечение отношений rj соответствует функции принадлежности: 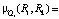
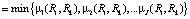 , то есть заданные отношения рассматриваются как одинаково важные. Если они различаются по важности, то факт их различия можно учесть, используя весовые коэффициенты в выражении µQ1 (Ri, Rk).
, то есть заданные отношения рассматриваются как одинаково важные. Если они различаются по важности, то факт их различия можно учесть, используя весовые коэффициенты в выражении µQ1 (Ri, Rk).
Конечной целью задачи выбора в множестве (x, R) является выбор подмножества недоминируемых альтернатив.
В множестве (x, µQ1(x)) подмножество недоминируемых альтернатив µNDQ1(x) вычисляется по следующему алгоритму:
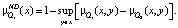 (3)
(3)
Нечеткое отношение Q1 которого вычисляется по алгоритму:
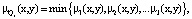 (4)
(4)
то есть является пересечением исходных отношений и позволяет выделить нечеткое подмножество недоминируемых альтернатив в множестве (x, µQ1(x)).
Кроме µQ1(x, y), вычисляется также функция µQ2(x, y):
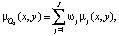 (5)
(5)
где при одинаковых по важности признаках ωj = 1/J (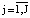 ) функция µQ2(x, y) упорядочивает альтернативы по степени их недоминируемости.
) функция µQ2(x, y) упорядочивает альтернативы по степени их недоминируемости.
Затем в множестве (x, µQ2(x)) выделяется подмножество недоминируемых альтернатив:
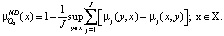 (6)
(6)
Тогда рациональный выбор альтернативы осуществляется как пересечение множеств µNDQ1(x) и µNDQ2(x):
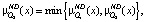 (7)
(7)
а в качестве альтернативы следует выбрать xND по правилу:
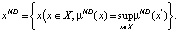 (8)
(8)
Алгоритм 2. В соответствии с этим алгоритмом эксперт сравнивает конструкционные признаки, оценивая их относительную важность, в результате формируется матрица A относительных весов признаков и матрица Bj (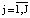 ) относительных весов аппаратов по каждому признаку.
) относительных весов аппаратов по каждому признаку.
В соответствии с алгоритмом по известной матрице A восстанавливаются истинные значения относительных весов признаков, что эквивалентно нахождению нормированного к единице собственного вектора xmax матрицы A. Собственный вектор xmax = {x1, x2, … xJ} матрицы, соответствующий ее максимальному собственному числу ωm (ωm ≥ m), получается в результате решения векторного уравнения:
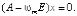 (9)
(9)
Вектор x ≠ 0 удовлетворяет уравнению:
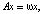 (10)
(10)
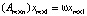 (11)
(11)
и называется собственным вектором матрицы A, соответствующим собственному числу ω.
Для того чтобы число ω было собственным числом матрицы A, необходимо и достаточно, чтобы выполнялось равенство:
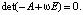 (12)
(12)
Собственный вектор матрицы экспертной оценки относительных весов признаков представляет истинные значения относительных весов. Аналогично собственные векторы матриц экспертной оценки (пригодности) аппаратов по каждому признаку восстанавливают их истинные значения. Второй этап состоит в выборе наиболее благоприятной альтернативы.
Алгоритм выбора адекватного структурного типа химико-технологических систем. Назначение алгоритма – поиск типа аппаратурной структуры многоассортиментного производства, адекватной производимой продукции. Исходной информацией является матрица An×m инцидентности типов технологического оборудования производимым продуктам, элементы которой имеют вид:
 (13)
(13)
Над матрицей An×m выполняются последовательно операции транспонирования, умножения на транспонированную матрицу и преобразования полученной симметричной матрицы в хессенбергову матрицу H, то есть следующая цепочка операций: 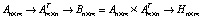 , где элементы матрицы Hn×m вычисляются в соответствии со следующим правилом:
, где элементы матрицы Hn×m вычисляются в соответствии со следующим правилом:
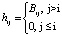 (14)
(14)
Структура матрицы Hn×m определяет допустимые типы структуры технологической подсистемы многоассортиментного производства. Если 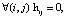 то допустима организация производства только в виде индивидуальных технологических схем. Если
то допустима организация производства только в виде индивидуальных технологических схем. Если 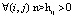 , то кроме индивидуальных схем допустимы совмещенные; при этом более полная совмещенность возможна, если
, то кроме индивидуальных схем допустимы совмещенные; при этом более полная совмещенность возможна, если 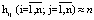 . Если
. Если 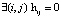 и
и 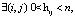 то наряду с индивидуальными и совмещенными схемами возможны также гибкие. Таким образом, алгоритм заключается в вычислении матрицы H и выводе ее на экран.
то наряду с индивидуальными и совмещенными схемами возможны также гибкие. Таким образом, алгоритм заключается в вычислении матрицы H и выводе ее на экран.
Алгоритм формирования временных ограничений. Сокращение общего времени на производство всех продуктов ассортимента в гибких системах достигается объединением продуктов в группы, производимые одновременно. Объединение продуктов в группы производится по признаку их аппаратурной аналогии на основе матрицы инцидентности А, элементы которой имеют следующий вид:
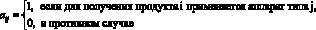 (15)
(15)
Чтобы определить число единиц оборудования, общее для продуктов Pi, Pk, достаточно сформировать матрицу В по правилу:
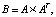 (16)
(16)
где AT – транспонированная матрица A.
Матрица B является основой для определения бинарных комбинаций продуктов, которые могли бы производиться в системе одновременно. Алгоритм генерации допустимых бинарных комбинаций продуктов по матрице B состоит в поэлементном сравнении ее строк и столбцов. Аналогично определяются допустимые тернарные комбинации продуктов и их комбинации более высокой арности.
В системе ограничений задачи параметрической оптимизации должны содержаться временные ограничения: время работы оборудования, на котором продукты выпускаются последовательно, должно суммироваться, и эта сумма не должна превышать годового фонда времени; последовательно выпускаемые продукты определяются в результате анализа матрицы H, а именно, допустимыми считаются бинарные комбинации продуктов, которым в матрице H соответствуют нулевые элементы. Для формирования временных ограничений выполняется поэлементное сравнение строк и столбцов матрицы H и определяются тернарные комбинации последовательно производимых продуктов и их комбинации более высокой парности.
Параметрическая оптимизация ХТС. Параметрическая оптимизация химико-технологических систем состоит в поиске определяющих размеров, производительности, значений конструкционных параметров технологического оборудования и режимных параметров технологических процессов, при которых достигается минимум критерия приведенных затрат. Алгоритмы параметрической оптимизации ориентированы на структурные типы технологических систем, определяемые следующими признаками: количеством производимых продуктов, временным режимом работы аппаратов и способом их коммутации в схеме [5; 8].
По количеству производимых продуктов различаются индивидуальные и многопродуктовые технологические системы; по временному режиму работы оборудования – системы, содержащие аппараты только периодического и содержащие аппараты периодического и полунепрерывного действия, взаимодействующие непосредственно или через демпфирующие емкости-накопители; кроме того, существенными признаками для алгоритмов оптимизации являются стандартизация оборудования и зависимость продолжительности циклов аппаратов периодического действия от массового размера партии продуктов.
Практически все технологические схемы, применяющиеся в производстве ЛКМ исследуемого ассортимента, создаются и проектируются на базе стандартного технологического оборудования, поэтому на эти схемы ориентированы разработанные алгоритмы параметрической оптимизации [12]. Продолжительность цикла технологических аппаратов задана в технологических регламентах и, следовательно, считается фиксированной, не зависящей от массового размера порции продуктов.
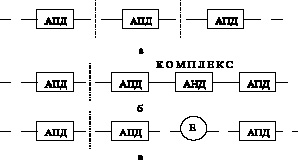
Рис. 2. Основные способы взаимодействия технологических аппаратов в ХТС производства ЛКМ: а) индивидуальные, содержащие непосредственно взаимодействующие аппараты периодического действия (АПД); б) индивидуальные, содержащие непосредственно взаимодействующие аппараты периодического (АПД) и полунепрерывного действия (АНД); в) индивидуальные, содержащие аппараты периодического действия, взаимодействующие через демпфирующие емкости-накопители (Е)
Таким образом, практическое значение для оптимизации технологических систем малотоннажных лакокрасочных производств имеют вычислительные алгоритмы, ориентированные на следующие классы технологических систем (рис. 2): индивидуальные, содержащие непосредственно взаимодействующие аппараты периодического действия (рис. 2а); индивидуальные, содержащие непосредственно взаимодействующие аппараты периодического и полунепрерывного действия (рис. 2б); индивидуальные, содержащие аппараты периодического действия, взаимодействующие через демпфирующие емкости-накопители (рис. 2в); индивидуальные, содержащие аппараты периодического и полунепрерывного действия, взаимодействующие через демпфирующие емкости-накопители; совмещенные (по технологическим процессам), содержащие непосредственно взаимодействующие аппараты периодического действия; совмещенные на основе непосредственно связанных аппаратов периодического и полунепрерывного действия; совмещенные на основе аппаратов периодического действия, взаимодействующих через демпфирующие емкости-накопители; совмещенные на основе аппаратов периодического и полунепрерывного действия, взаимодействующих через емкости-накопители; гибкие, содержащие непосредственно взаимодействующие аппараты периодического действия; гибкие, содержащие аппараты периодического и полунепрерывного действия, взаимодействующие непосредственно; гибкие на основе аппаратов периодического действия, взаимодействующих через емкости-накопители; гибкие на основе аппаратов периодического и полунепрерывного действия, взаимодействующих через емкости-накопители.
Наиболее общим структурным типом является тип гибких ХТС, содержащих аппараты периодического и полунепрерывного действия, взаимодействующих через емкости-накопители. Задача параметрической оптимизации систем этого типа имеет следующую формулировку. Задан ассортимент n продуктов P = {P1, P2, ..., Pn}, получающихся в результате n частично совмещенных технологических процессов; известны технологические маршруты получения продуктов; задан объем выпуска каждого продукта: G = {G1, G2, ..., Gn}. Известны уравнения стадийных или операционных материального и энергетического балансов; определяющие размеры и производительность стандартного технологического оборудования, заданные в виде параметрических рядов. Заданы предельные коэффициенты заполнения объема емкостных аппаратов. Требуется определить размер, производительность и количество аппаратов, оформляющих каждую стадию многостадийного технологического процесса и объем демпфирующих емкостей, при которых достигается минимум приведенных затрат на оборудование. Аппаратурная структура системы считается определенной на этапе структурной оптимизации и, следовательно, фиксированной.
Оптимизация аппаратурного состава индивидуальных ХТС. Индивидуальные ХТС с непосредственно взаимодействующими аппаратами периодического действия. Если количество аппаратов, оформляющих стадию технологического процесса, фиксировано − обычно Nj = 1 (рис. 2а), – то степени свободы у системы этого типа отсутствуют, и можно найти единственный вариант аппаратурного оформления технологического процесса, выбрав подходящие размеры аппаратов из содержащихся в параметрических рядах, для чего необходимо решить относительно k уравнение:
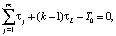 (17)
(17)
где τj – продолжительность технологического цикла аппарата j; τL – продолжительность технологического цикла системы; k – количество партий продукта; T0 – годовой фонд времени.
Решив уравнение (17) относительно k, определим k’ = sup k, то есть ближайшее целое, большее k, и рассчитаем величину массового размера партии продукта:
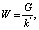 (18)
(18)
где G – годовая производительность проектируемой установки.
Зная W, рассчитаем определяющие точные размеры аппаратов периодического действия:
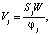 (19)
(19)
где Sj – материальный индекс стадии j; φj – коэффициент заполнения объема аппарата.
Округлим полученные значения Vj до ближайших больших Vj’, содержащихся в параметрических рядах, и проверим принадлежность фактического коэффициента заполнения заданному интервалу 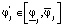 :
:
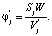 (20)
(20)
Если это условие выполняется, то рассчитаем приведенные затраты на основное оборудование по формуле:
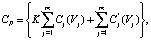 (21)
(21)
где K – нормативный коэффициент окупаемости; Cj – стоимость аппарата j; С’j – эксплуатационные затраты.
Несколько усложняется расчет системы, когда продолжительность цикла аппаратов зависит от массового размера порции продукта. В системах этого типа продолжительность цикла аппаратов должна рассчитываться, для чего следует сначала задать начальное приближение величины массового размера партии продукта. У систем этого типа появляется степень свободы и, следовательно, возможность оптимизации аппаратурного состава. Массовый размер партии продукта определяется по минимальному размеру аппарата последней стадии технологического процесса в параметрическом ряду. После этого уравнение (17) решается относительно k и выполняется расчет схемы, как в предыдущем случае.
Если количество аппаратов Nj 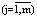 и их размеры Vj
и их размеры Vj 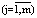 являются варьируемыми переменными, а продолжительность технологических циклов аппаратов фиксирована τj = const
являются варьируемыми переменными, а продолжительность технологических циклов аппаратов фиксирована τj = const 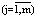 и определяется технологическим регламентом, то у системы имеются степени свободы и возможна задача оптимизации, которая имеет следующий вид:
и определяется технологическим регламентом, то у системы имеются степени свободы и возможна задача оптимизации, которая имеет следующий вид:
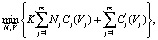 (22)
(22)
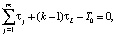
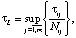 (23)
(23)
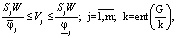 (24)
(24)
где Vj – дискретные переменные; k, Nj – целочисленные переменные; g, τL – непрерывные переменные.
Ниже кратко описан алгоритм оптимизации аппаратурного состава ХТС данного типа.
Примем Nj = 1 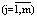 и решим задачу, описанную в начале раздела. Определим стадию с максимальной продолжительностью и увеличим количество аппаратов на этой стадии на 1, заставив работать их с равномерным смещением по времени. Продолжим решение, увеличивая количество аппаратов на лимитирующей стадии на единицу и повторяя расчет. Описанный алгоритм представляет собой алгоритм направленного перечисления вариантов и может быть применен для задач оптимизации небольшой размерности.
и решим задачу, описанную в начале раздела. Определим стадию с максимальной продолжительностью и увеличим количество аппаратов на этой стадии на 1, заставив работать их с равномерным смещением по времени. Продолжим решение, увеличивая количество аппаратов на лимитирующей стадии на единицу и повторяя расчет. Описанный алгоритм представляет собой алгоритм направленного перечисления вариантов и может быть применен для задач оптимизации небольшой размерности.
Индивидуальные ХТС, содержащие непосредственно взаимодействующие аппараты периодического и полунепрерывного действия. Если количество аппаратов Nj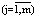 и продолжительность их технологического цикла
и продолжительность их технологического цикла 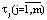 фиксирована, то оптимизация аппаратурного состава невозможна. Расчет системы этого типа содержит предварительную ее декомпозицию на последовательность автономных аппаратов периодического действия и комплексов, состоящих из взаимосвязанных последовательностей аппаратов периодического и полунепрерывного действия (рис. 2б).
фиксирована, то оптимизация аппаратурного состава невозможна. Расчет системы этого типа содержит предварительную ее декомпозицию на последовательность автономных аппаратов периодического действия и комплексов, состоящих из взаимосвязанных последовательностей аппаратов периодического и полунепрерывного действия (рис. 2б).
Продолжительность технологического цикла подсистемы определяется следующим выражением:
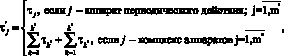 (25)
(25)
где m’, m’’ – соответственно количество автономных аппаратов периодического действия и автономных комплексов; k’, k’’ – соответственно количество аппаратов периодического действия и непрерывного действия, образующих автономный комплекс. Расчет схемы производится по алгоритму, аналогичному алгоритму расчета схемы, изложенному в начале раздела.
Если варьируемыми переменными являются размер Vj и количество аппаратов Nj, то возможна задача оптимизации, аналогичная ранее рассмотренной, но продолжительность цикла системы рассчитывается по формуле:
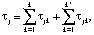 (26)
(26)
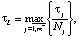 (27)
(27)
где m’’’ – общее число аппаратов периодического действия и автономных комплексов.
К системе ограничений задачи оптимизации должно быть добавлено условие, гарантирующее необходимую производительность Pj оборудования непрерывного действия:
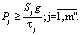 (28)
(28)
Индивидуальные ХТС, содержащие емкости–накопители. Для производства ЛКМ характерен только один способ взаимодействия технологических аппаратов через демпфирующие емкости: такой, в котором подающий аппарат – периодического действия, а принимающий – непрерывного действия. Этот структурный тип технологических систем реализован в производстве пигментированных ЛКМ, в котором подающим аппаратом является периодически действующий диссольвер, а принимающим – непрерывно действующая бисерная машина. Транспорт массы из диссольвера в демпфирующую емкость и из нее в бисерную машину осуществляется шестеренчатыми насосами. Оптимизирующими переменными в схемах этого типа являются определяющие размеры и количество единиц основного технологического оборудования, объем демпфирующей емкости, массовый размер порции продукта, продолжительность технологического цикла системы, минимальный объем массы в демпфирующих емкостях, число порций продукта. В качестве независимых переменных можно принять, например, размер и количество единиц основного технологического оборудования и объем демпфирующих емкостей (рис. 3).
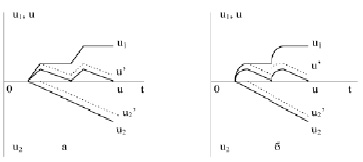
Рис. 3. Графики загрузки (u1), разгрузки (u2, u2’) демпфирующей емкости и изменения объема реакционной массы в ней (u, u’): а) при разгрузке насосом и сжатым газом; б) при разгрузке под давлением гидростатического столба
Загрузка емкости из диссольвера осуществляется периодически, а разгрузка – непрерывно. Следовательно, функция u(t, Δτ) – разрывная, определяемая следующим соотношением:
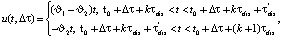 (29)
(29)
где ϑ1, ϑ2 – производительность насосов, м3/ч; τdis – продолжительность технологического цикла диссольвера, ч; τ’dis – продолжительность загрузки партии продукта из диссольвера в емкость, ч; Δt = t1 – t0; k = 0,1,2, ...
Необходимо обеспечить режим, при котором 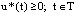 , где T – период функции,
, где T – период функции, 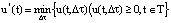 .
.
Тогда объем демпфирующей емкости должен удовлетворять условию:
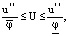 (30)
(30)
где 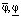 – соответственно верхний и нижний пределы коэффициента заполнения ее объема, а
– соответственно верхний и нижний пределы коэффициента заполнения ее объема, а 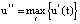 .
.
Это условие служит основанием для выбора емкости из параметрического ряда. Поиск экстремума унимодальной функции u*(t) производится методом золотого сечения.
При первом способе функция u(t, Δτ) имеет вид:
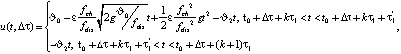 (31)
(31)
где ϑ0 – начальный объем массы в диссольвере; fdis, fch – площадь сечения диссольвера и разгрузочного штуцера, м2; ɛ – коэффициент сжатия струи; g – ускорение силы тяжести, м/c2.
Во втором случае функция u(t, Δτ) имеет вид:
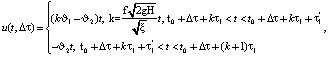 (32)
(32)
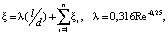 (33)
(33)
где λ – коэффициент гидравлического трения; l – общая длина трубы, м; d – диаметр трубы для передавливания, м; ξi – коэффициент местных сопротивлений; Re – число Рейнольдса.
Расчет требуемого напора установки определяется по формулам [14]:
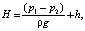 (34)
(34)
где h – геометрическая высота трубы для передавливания, м; p1, p2 – давление газа в диссольвере и в емкости, Па; ρ – плотность массы, кг/м3; g – ускорение силы тяжести, м/c2.
Индивидуальные ХТС с комбинированным режимом взаимодействия технологических аппаратов. Системы этого класса подлежат предварительной декомпозиции на относительно автономные подсистемы, рассматриваемые как блоки периодического действия (рис. 2в). Декомпозиция системы производится по сечениям непосредственной связи между аппаратами, в результате декомпозиции получаются подсистемы, образованные отдельными аппаратами периодического действия и комплексами аппаратов непрерывного и периодического действия, взаимодействующих через емкость.
Оптимизация аппаратурного состава многопродуктовых ХТС. Системы с непосредственным взаимодействием технологических аппаратов. Если количество аппаратов Nj и продолжительность их циклов tij фиксированы, то в общем случае при существенном различии значений стадийных материальных индексов получения различных продуктов задача решения не имеет, так как аппараты имеют фиксированные размеры, а материальные индексы продуктов значительно различаются.
Если количество аппаратов Nj и их определяющие размеры Vj являются оптимизируемыми переменными, то задача имеет следующую формулировку:
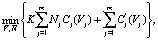 (35)
(35)
при
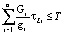
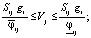
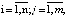 (36)
(36)
где
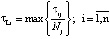 (37)
(37)
при дискретных Vj и целочисленных Nj.
Для решения задачи разработан модифицированный эвристический алгоритм, основанный на представлении о гипотетическом продукте. Алгоритм состоит из трех этапов: расчет точных размеров оборудования при фиксированном количестве параллельных аппаратов; округление полученных точных значений размеров до ближайших, содержащихся в стандартных параметрических рядах; выбор количества параллельных аппаратов [12]. Ниже приводится описание алгоритма оптимизации.
Выполним декомпозицию ХТС на квазиавтономные подсистемы по связям между аппаратурными блоками периодического действия, как показано на рис. 2б. В результате декомпозиции исходная система представляется в виде последовательно соединенных подсистем, количество которых на единицу превышает число связей между аппаратами периодического действия. Обозначим j – текущий номер подсистемы 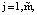 где
где 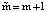 . Подсистемы образованы либо блоками параллельно соединенных аппаратов периодического действия, либо группами последовательно соединенных аппаратов периодического и полунепрерывного действия. Таким образом, в системе содержатся подсистемы двух видов. В свою очередь в подсистемах, состоящих из аппаратов периодического и полунепрерывного действия, последние могут образовывать последовательные цепочки произвольной длины.
. Подсистемы образованы либо блоками параллельно соединенных аппаратов периодического действия, либо группами последовательно соединенных аппаратов периодического и полунепрерывного действия. Таким образом, в системе содержатся подсистемы двух видов. В свою очередь в подсистемах, состоящих из аппаратов периодического и полунепрерывного действия, последние могут образовывать последовательные цепочки произвольной длины.
Определим продолжительность технологического цикла квазиавтономной подсистемы следующим образом:
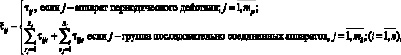 (38)
(38)
где Rj, Sj – соответственно количество аппаратов периодического действия и групп последовательно соединенных аппаратов полунепрерывного действия в подсистеме j.
Очевидно, что квазиавтономные подсистемы могут соединятся параллельно, образуя блоки и вводиться в действие с временным смещением, что позволяет сократить продолжительность технологического цикла, определяемую для блока идентичных подсистем следующим образом:
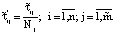 (39)
(39)
Тогда продолжительность технологического цикла системы определится по формуле:
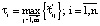 (40)
(40)
Временное ограничение для систем с фиксированной структурой a priori задано, так как продукты в системе производятся последовательно, а системы временных ограничений для ХТС с перестраиваемой структурой формируются по специальному алгоритму на стадии структурной оптимизации; она однозначно соответствует оптимальной в смысле затрат времени дисциплине выпуска продуктов.
Опишем модифицированный эвристический алгоритм оптимизации аппаратурного состава систем этого класса, основанный на представлении о гипотетическом продукте, учитывающем продолжительность переходного периода работы системы при каждом изменении номенклатуры производимого продукта. Для этого определим сначала величину стадийных материальных индексов гипотетического продукта:
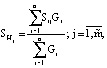 (41)
(41)
где Sij – материальный индекс стадии j для продукта i; Gi – объем выпуска продукта i.
Рассчитаем затем фактор размера Fi по формуле:
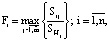 (42)
(42)
который по смыслу есть отношение массовых размеров партий фактического и гипотетического продуктов.
Если окажется, что объемы реакционной массы, перерабатываемой на всех стадиях процесса для получения любого из продуктов [15], меньше соответствующих объемов гипотетического продукта, то первоначально принятое значение материального индекса SHj гипотетического продукта следует уменьшать до тех пор, пока оно не достигнет максимального из них, то есть:
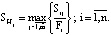 (43)
(43)
Тогда при выбранных размерах аппаратов периодического действия массовый размер партии продуктов определится следующим образом:
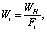 (44)
(44)
где WH – размер партии гипотетического продукта.
Число партий фактических продуктов, производимое в течение годового фонда времени, определяется выражением:
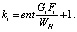 (45)
(45)
Общее время, затрачиваемое на производство продукта i, определится по формуле:
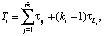 (46)
(46)
а общее время выпуска всех продуктов на данном оборудовании определится системой временных ограничений:
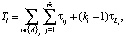 (47)
(47)
где l – номер группы продуктов (l = 1, 2, …,).
Очевидно, что Tl ≤ T, где T – годовой фонд времени.
Размер порции гипотетического продукта следует выбирать таким образом, чтобы выполнялись ограничения Tl ≤ T.
Размер аппаратов периодического действия выбирается таким образом, чтобы:
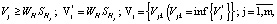 (48)
(48)
а производительность аппаратов полунепрерывного действия:
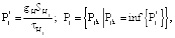 (49)
(49)
где 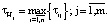
Перед началом работы алгоритма Nj = 1. В процессе расчета для стадии, у которой SHj минимальна, количество аппаратов увеличивается на единицу, и расчет повторяется. Величина Nj наращивается до тех пор, пока стоимость оборудования не перестанет возрастать в пределах 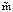 циклов расчета, где
циклов расчета, где 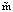 – общее количество квазиавтономных стадий.
– общее количество квазиавтономных стадий.
Системы с комбинированным режимом взаимодействия технологических аппаратов (непосредственное и через емкость). Выполним декомпозицию ХТС на квазиавтономные подсистемы по непосредственным связям между аппаратами периодического действия (рис. 2в). Исходная система представляется в виде подсистем, образованных либо отдельными аппаратами периодического действия, либо комплексами последовательно соединенных аппаратов периодического и полунепрерывного действия, либо группами подающих и принимающих аппаратов, связанных вспомогательной емкостью. Рассмотрим наиболее типичный случай взаимодействия «подающий аппарат работает в периодическом режиме, принимающий – в непрерывном режиме».
Алгоритм оптимизации аппаратурного состава организуется в виде двухуровневой процедуры, в которой на верхнем уровне оптимизируются размеры и количество стандартного технологического оборудования, а на нижнем – объем промежуточных емкостей. Алгоритм верхнего уровня, по существу, есть повторение описанного ранее алгоритма оптимизации аппаратурного состава с непосредственным взаимодействием оборудования. Алгоритм нижнего уровня состоит в оптимизации объема реакционной массы, содержащейся во вспомогательных емкостях:
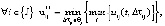 (50)
(50)
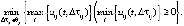 (51)
(51)
Определим 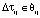 , при которых
, при которых 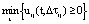 , методом дихотомии; примем
, методом дихотомии; примем 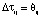 , где
, где 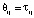 , первоначальный интервал поиска
, первоначальный интервал поиска 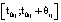 . Если
. Если 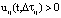
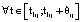 , что определяется сканированием по t с шагом Δt, то примем
, что определяется сканированием по t с шагом Δt, то примем 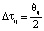 и рассмотрим интервал
и рассмотрим интервал 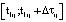 . После того как определено
. После того как определено 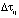 , при котором
, при котором 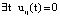 , определим максимум
, определим максимум 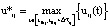 методом золотого сечения. Тогда объем Uj демпфирующей емкости должен удовлетворять условию:
методом золотого сечения. Тогда объем Uj демпфирующей емкости должен удовлетворять условию:
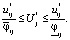 (52)
(52)
Примем
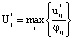 ;
; 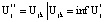 ,
,
то есть выберем из стандартного ряда аппарат объема, ближайшего большего к рассчитанному.
Заключение
Авторским коллективом обоснована организация производства ЛКМ, принципиально отличающаяся от традиционной, ориентированная на системы с перестраиваемой структурой и блочно-модульное оформление технологических процессов малотоннажных лакокрасочных производств. Разработана структурно-функциональная схема прототипа интегрированной экспертной системы, ориентированной на автоматизацию проектирования и оптимизацию режимов функционирования малотоннажных производств ЛКМ. Создано математическое и программное обеспечение расчетной подсистемы интегрированной экспертной системы, ориентированное на оптимизацию структуры и аппаратурного состава химико-технологических систем производства ЛКМ. Разработанный комплекс программ структурной и параметрической оптимизации реализован в экспертно-информационной системе для проектирования гибких производственных систем малотоннажных многоассортиментных лакокрасочных производств Paint Expert.
Выполняемый программный файл экспертной системы дополняется рядом «библиотек динамических ссылок», служащих для уменьшения объёма оперативной памяти ЭВМ, занимаемого программой в процессе выполнения, за счёт организации их динамического отображения в адресное пространство процесса и выгрузки из него по мере необходимости использования тех или иных функций. Программное обеспечение активно использует научный и проектный отдел, конструкторское бюро, машиностроительный завод, входящие в структуру НПО «Лакокраспокрытие» (г. Хотьково).
Библиографическая ссылка
Болдырев В.С., Меньшиков В.В., Быков А.Е., Кузнецов С.В., Савина А.С., Богатов Н.А. РАЗРАБОТКА АЛГОРИТМОВ ЭКСПЕРТНОЙ И ИНФОРМАЦИОННОЙ СИСТЕМ ПРОЕКТИРОВАНИЯ МАЛОТОННАЖНЫХ МНОГОАССОРТИМЕНТНЫХ ЛАКОКРАСОЧНЫХ ПРОИЗВОДСТВ // Современные наукоемкие технологии. 2021. № 8. С. 38-51;URL: https://top-technologies.ru/ru/article/view?id=38778 (дата обращения: 01.02.2026).
DOI: https://doi.org/10.17513/snt.38778



