В монографии [1] приведено определение комплексных эмоций робота. Также введено определение воспитания робота. Программист может ставить перед собой цель добиться заданного воспитания робота. При этом возникает задача контроля достижения роботом поставленной воспитательной цели на каждом этапе воспитания.
Актуальность данной статьи продиктована необходимостью нахождения способов численной оценки достижения воспитательной цели.
Цель данной статьи состоит в построении математических моделей эмоционального состояния робота и целеустремленности робота при достижении поставленной воспитательной цели.
Общая математическая модель цели воспитания робота
Пусть задана цель воспитания робота, определяемая соотношением:
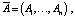
где Ai > 0,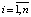 
n – количество базовых эмоций в комплексной эмоции робота [1].
Пусть вектор воспитаний робота, полученных в результате возникших у него эмоций в ответ на раздражающий стимул, имеет вид:
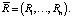
Пусть ψ – угол между векторами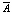 
и 
.
И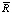звестно, что скалярное произведение векторов удовлетворяет соотношению [2]:
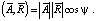
Следовательно, косинус угла ψ между векторами можно определить по формуле:
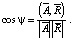
По определению проекции [2] справедливо равенство:
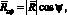
где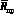 
– это проекция вектора 
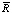на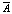 
.
Таким образом, интегральную характеристику δ, описывающую величину достижения поставленной воспитательной цели при заданном воспитании робота, можно вычислить по следующей формуле:
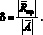
Пусть α = cos ψ, тогда справедливо соотношение:
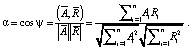(1)
Очевидно соотношение: α∈[–1, 1].
Величину α назовем целеустремленностью робота при достижении воспитательной цели.
Очевидно то, что большему численному значению α соответствует большая целеустремленность к цели воспитания.
Справедлива цепочка равенств:
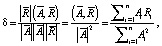(2)
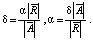
Общая математическая модель достижения цели для гармонических эмоций робота
В монографии [1] описывается элементарная эмоция в виде гармонической функции
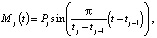
где t∈[tj–1, tj], Pj = const, t – текущий момент времени, tj–1 – момент времени начала действия элементарной эмоции, tj – момент времени окончания действия элементарной эмоции, j – номер такта.
Исходя из предыдущей формулы и работы [1] вычислим элементарное воспитание робота:
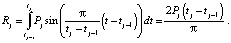
Отсюда следует, что вектор воспитаний робота, полученный на такте с номером j, будет иметь вид:
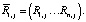
Тогда становится очевидным соотношение:
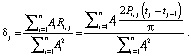(3)
В работе [1] предложено элементы вектора комплексного эмоционального воспитания робота вычислять по формуле:
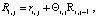
где j – номер такта,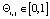 
– коэффициент памяти, ri,j – элементарное воспитание.
С учетом коэффициентов памяти робота справедливы соотношения:
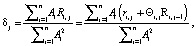(4)
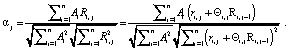(5)
Рассмотрим разность интегральных характеристик достижения цели для двух последовательных тактов, где δj – значение величины достижения поставленной цели при воспитательном такте с порядковым номером j.
Очевидна следующая цепочка равенств:
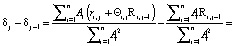
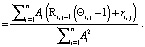(6)
Сформулируем следующую теорему.
Теорема 1.
При стремлении воспитания к цели воспитания должно выполняться условие:
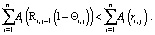(7)
Доказательство.
Очевидно, что при достижении цели разность δj – δj–1 должна быть положительна, т.е. должно выполняться неравенство:
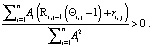
Преобразовывая полученное неравенство и учитывая то, что знаменатель дроби всегда положительный и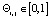 
, получаем неравенство (7).
Таким образом, теорема доказана.
Из теоремы 1 следует несколько выводов.
1. Если коэффициент памяти равен нулю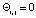 
, то
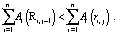(8)
Если элементарное воспитание на текущем такте превосходит воспитание на предыдущем такте, тогда воспитание будет приближаться к цели.
2. Если робот обладает абсолютной памятью [1] (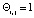
), то
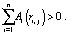(9)
3. Если робот равномерно забывчивый [3, 4] (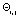
не зависит от номера такта j), то
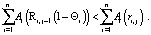(10)
Очевидно, что воспитание робота стремится к воспитательной цели, если элементарное воспитание на текущем такте превосходит некоторую «забытую» долю воспитания на предыдущем такте.
Очевидно, что, чем ближе воспитательный процесс приближается к цели воспитания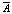 
, тем больше забываемая величина текущего воспитания и тем больше должно быть элементарное воспитание ri,j.
Исследование математической модели достижения цели при комплексных гармонических эмоциях
Очевидна цепочка равенств:
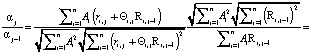
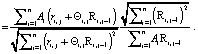(11)
Рассмотрим только положительные целеустремленности α, которые приближают робота к цели воспитания.
Тогда необходимое условие приближения к цели воспитания описывается соотношениями:
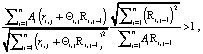
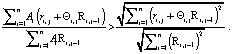(12)
Рассмотрим равномерно забывчивого робота с равноценными эмоциями. Согласно [5] для такого робота воспитание вычисляется по формуле:
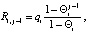
где qi – элементарное воспитание робота, i – постоянное для каждого такта j.
Справедлива следующая цепочка равенств:
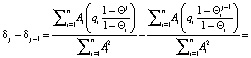
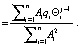(13)
Описанная выше цепочка равенств дает основание утверждать, что, если qi имеет один знак с Ai, то δj будет возрастающей последовательностью, что определяет увеличение значения достижения поставленной воспитательной цели.
Рассмотрим разность интегральных характеристик достижения воспитательной цели для гармонических эмоций.
Для гармонических эмоций справедлива следующая цепочка равенств:
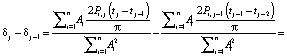
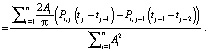(14)
Анализ цепочки равенств позволяет утверждать, что для того, чтобы разность δj – δj–1 была положительной, требуется совпадение по знаку величин Ai и Pi (независимо от номера такта j), а также длительность воздействия или амплитуда эмоции Pi,j каждой последующей эмоции должна увеличиваться с увеличением номера такта j.
Рассмотрим разность интегральных характеристик δj – δj–1 достижения цели для гармонических эмоций, когда такты равны между собой tj – tj–1 = t.
Для этого случая справедлива цепочка равенств:
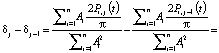
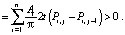(15)
Отсюда следует, что для приближения воспитания к цели знак разности (Pi,j – Pi,j–1) должен совпадать со знаком Ai.
В статье [6] описываются гармонические эмоции и гармонические воспитания робота, а также предложены базисы гармонических воспитаний. Рассмотрим базис для гармонических воспитаний при Pi,j = 1. Этот базис имеет вид:
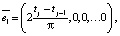
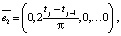
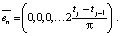
Очевидно, что цель воспитания и полученное воспитание по гармоническому базису имеют вид [7]:
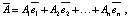
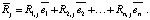
Сформулируем следующую теорему.
Теорема 2. Базис гармонических эмоций порождает базис гармонических воспитаний.
Доказательство
Рассмотрим матрицу H, построенную на векторах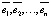 
[7]:
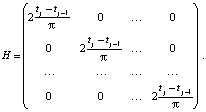
Определитель Δ данной матрицы имеет вид [7]:
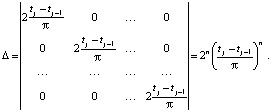
Поскольку длина такта tj – tj–1 ≠ 0, то данный определитель не равен нулю. Отсюда следует, что базис гармонических воспитаний действительно будет базисом.
Таким образом, интегральная характеристика достижения цели δj сама по себе описывается через базис гармонических воспитаний и имеет вид:
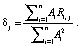(16)
В РФ разработана программная система численной оценки психоэмоционального состояния человека VibraImage [8]. Система позволяет автоматически вычислять и визуально оценивать психоэмоциональное состояние человека с помощью компьютерной обработки телевизионного сигнала и его преобразования в виброизображение. Психоэмоциональное состояние человека характеризуется на основе запатентованных авторами разработки алгоритмов анализа вестибулярно-эмоционального рефлекса и макродвижений. Система VibraImage анализирует и регистрирует более 20 параметров виброизображения и позволяет пользователю осуществлять настройку системы в соответствии со своими задачами и определять требуемые психофизиологические параметры человека.
Заключение
Таким образом, в настоящей статье впервые доказано, что базис гармонических воспитаний является базисом; впервые рассмотрены условия достижения роботом цели воспитания, а также сформулирована теорема об условиях достижения роботом поставленной воспитательной цели при разных коэффициентах памяти робота. По приведенным в статье результатам становится возможным определять величину достижения роботом поставленной воспитательной цели и формулировать условия достижения цели за определенное количество воспитательных тактов.
Практическая значимость результатов, представленных в данной статье, позволяет проектировать воспитание групп роботов исходя из того, что каждый робот группы имеет общую цель воспитания, разные векторы воспитания в настоящий момент времени и разные коэффициенты памяти. На основе математических моделей роботов, предложенных в настоящей статье, можно использовать программу VibraImage для хотя бы весьма приближенного вычисления достижения поставленной воспитательной цели человеком согласно измеренным его воспитаниям с помощью компьютера.
Библиографическая ссылка
Анисимова С.И. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИНТЕГРАЛЬНОГО ВОСПИТАНИЯ КОМПЛЕКСНЫХ ЭМОЦИЙ РОБОТА // Современные наукоемкие технологии. – 2021. – № 8. – С. 9-15;URL: https://top-technologies.ru/ru/article/view?id=38774 (дата обращения: 20.04.2024).