Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ромм Я.Е. 1 Буланов С.Г. 1

---

1 Таганрогский институт имени А.П. Чехова (филиал) ФГБОУ ВО «РГЭУ (РИНХ)»

Устойчивость в смысле Ляпунова анализируется с помощью приближенных методов решения задачи Коши для обыкновенных дифференциальных уравнений. В числе применяемых методов – методы Эйлера, Рунге – Кутты, Батчера, Дормана – Принса, а также кусочно-интерполяционный метод с итерационным уточнением, построенный на основе интерполяционного полинома Лагранжа. Методы реализованы программно и сравниваются между собой на предмет эффективности выполнения компьютерного анализа устойчивости. Сравнение проводится в аспекте достоверности и временной сложности получения результатов анализа, конкретно – по длине отрезка приближенного решения, на котором сохраняется достоверная оценка устойчивости, и по времени выполнения анализа на равных отрезках. Для разностных методов выбирается один и тот же шаг решения одинаковой дифференциальной системы, кусочно-интерполяционный метод для этой же системы выбирается с фиксированными параметрами. Оценки устойчивости и параметры сравнения опираются на априори предложенные критерии. Анализируемые дифференциальные системы включают линейные системы с постоянными и переменными коэффициентами, автономные и нелинейные системы общего вида. Процесс сравнения выполняется посредством численного моделирования предложенных критериев устойчивости и реализуется по ходу решения задачи Коши. Результаты численного эксперимента показывают применимость для моделирования устойчивости каждого из рассматриваемых методов. Вместе с тем для компьютерного анализа устойчивости в реальном времени по ходу решения задачи предпочтителен кусочно-интерполяционный метод с итерационным уточнением на основе интерполяционного полинома Лагранжа. В работе также представлены результаты численного моделирования устойчивости на основе знаков приближения решения и его двух производных, в этом случае применяется метод Эйлера без сопоставления с другими методами.

Статья в формате PDF

1577 KB

критерии устойчивости по Ляпунову

численное моделирование устойчивости

компьютерный анализ устойчивости решений обыкновенных дифференциальных уравнений

сравнение методов численного моделирования

кусочно-интерполяционный метод с итерационным уточнением на основе полинома Лагранжа

1. Маркеев А.П., Сокольский А.Г. Некоторые вычислительные алгоритмы нормализации гамильтоновых систем. М.: Препринт ИПМ АН СССР. № 31, 1976. 61 с.

2. Hammarling S.J. Numerical Solution of the Stable, Non-negative Definite Lyapunov Equation. IMA J. of Num. Analysis. Vol. 2. Issue 3. 1. July 1982. P. 303–323.

3. Новиков М.А. О вычислительных способах достаточных условий устойчивости автономных консервативных систем // Современные технологии. Системный анализ. Моделирование. 2014. № 1 (41). С. 28–36.

4. Giesl P.A., Hafstein S.F. Computation of Lyapunov functions for nonlinear discrete time systems by linear programming. J. Difference Equ. Appl. 2014. 20. P. 610–640.

5. Ромм Я.Е. Мультипликативные критерии устойчивости на основе разностных решений обыкновенных дифференциальных уравнений // Кибернетика и системный анализ. 2006. № 1. С. 127–142.

6. Ромм Я.Е. Моделирование устойчивости по Ляпунову на основе преобразований разностных схем решений обыкновенных дифференциальных уравнений // Известия РАН. Математическое моделирование. 2008. Т. 20. № 12. С. 105–118.

7. Ромм Я.Е. Компьютерно-ориентированный анализ устойчивости решений дифференциальных систем // Современные наукоемкие технологии. 2020. № 4. С. 42–63.

8. Катрич С.А. Разработка и исследование программного моделирования устойчивости решений нелинейных дифференциальных уравнений на основе разностных методов: автореф. дис. … канд. техн. наук. Таганрог: Изд-во ТРТУ, 2006. 20 с.

9. Джанунц Г.А., Ромм Я.Е. Варьируемое кусочно-интерполяционное решение задачи Коши для обыкновенных дифференциальных уравнений с итерационным уточнением // Журнал вычислительной математики и математической физики. 2017. Т. 57. № 10. С. 1641–1660.

10. Romm Ya.E., Dzhanunts G.A. Piecewise interpolation solution of ordinary differential equations with application to numerical modeling problems. Journal of Physics. 2021. Conference Series. 1902(1). Р. 012130.

11. Демидович Б.П. Лекции по математической теории устойчивости. М.: Изд-во «Науку – всем», 2019. 480 с.

12. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1. СПб.: Лань, 2018. 608 с.

13. Джанунц Г.А. Компьютерный метод кусочно-полиномиального приближения решений обыкновенных дифференциальных уравнений в применении к моделированию автоколебательных реакций: автореф. дис. … канд. техн. наук. Таганрог: Изд-во ЮФУ, 2012. 22 с.

14. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971. 534 с.

15. Giesl P., Hafstein S. Computation of Lyapunov functions for nonlinear discrete time systems by linear programming. J. Difference Equ. Appl. 2014. Vol. 20, Issue 4. P. 610–640.

16. Миронов В.В., Митрохин Ю.С. Технологический подход к исследованию устойчивости динамических систем: прикладные вопросы // Вестник РГРТУ. 2017. № 59. С. 127–135.

17. Александров А.Ю., Жабко А.П., Косов А.А. Анализ устойчивости и стабилизация нелинейных систем на основе декомпозиции // Сибирский математический журнал. 2015. Т. 56. № 6. С. 1215–1233.

18. Baudouin L., Seuret A., Gouaisbaut F. Lyapunov stability analysis of a linear system coupled to a heat equation. In 20th IFAC World Congress, Toulouse. 2017. Vol. 50. P. 11978–11983.

Первоначально подход к анализу устойчивости в смысле Ляпунова (ниже – устойчивости) на основе численного моделирования обсуждался в [1, 2], современное состояние исследований отражено, в частности, в [3, 4]. В излагаемой ниже работе численное моделирование устойчивости опирается на разностное и кусочно-интерполяционное решение задачи Коши для системы обыкновенных дифференциальных уравнений (ОДУ), моделирование устойчивости выполняется по ходу компьютерного решения задачи на основе критериев, предложенных в [5–7]. Ранее в рамках данного подхода моделирование, как правило, выполнялось с помощью метода Эйлера, использование для этой цели разностных методов более высокого порядка практически не влияло на качество анализа устойчивости [8]. Однако на сопоставление методов в рассматриваемом аспекте повлияло появление кусочно-интерполяционного метода с итерационным уточнением на основе интерполяционных полиномов Ньютона [9] и Лагранжа [10]. Предложенные в [9, 10] методы отличаются непрерывностью и непрерывной дифференцируемостью приближенного решения, обладают сравнительно высокой точностью и малым накоплением погрешности на достаточно длинном отрезке приближения. На основании этих свойств можно предположить, что с помощью кусочно-интерполяционных методов сравнительно достоверно отображается асимптотическое поведение решения задачи Коши и адекватно оценивается устойчивость. Предварительный численный эксперимент отчасти подтверждает это предположение. Отсюда ставится задача провести системное сравнение методов Эйлера, Рунге – Кутты, Батчера, Дормана – Принса и кусочно-интерполяционного метода с итерационным уточнением на предмет численного моделирования асимптотического поведения решения задачи Коши для ОДУ и компьютерного анализа его устойчивости. Требуется сравнить степень достоверности и эффективность анализа в рамках предложенных критериев устойчивости. Для сравнения выбран набор дифференциальных систем различных классов. Все методы сравниваются между собой на каждой задаче в отдельности, с равным шагом, на равном отрезке приближения, – по временной сложности и по длине отрезка приближения, на котором сохраняется достоверность критериев устойчивости.

Цель исследования состоит в том, чтобы определить возможности каждого метода и выявить наиболее предпочтительный метод для инвариантного компьютерного анализа устойчивости по Ляпунову решений систем ОДУ различных классов.

Исходные соотношения и используемые критерии

Рассматривается задача Коши для системы вида

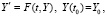(1)

где ,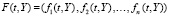

,

.

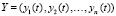Ниже используются канонические согласованные нормы матрицы и вектора. По умолчанию 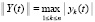, в численных экспериментах, помимо того, используется эвклидова норма. Всюду ниже предполагается, что ∃δ0 > 0, такое, что на полупрямой 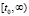выполнены все условия существования и единственности для невозмущенного решения и для каждого его возмущения 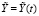, , 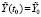с начальным вектором в границах 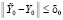. Для всех рассматриваемых в дальнейшем численных методов решения задачи (1) на отрезке 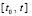будут предполагаться выполненными условия сходимости , .

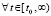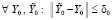В принятых условиях определение устойчивости упрощено: решение 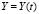устойчиво, если 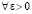найдется 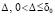, такое, что 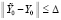влечет 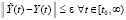. Решение асимптотически устойчиво, если оно устойчиво и найдется 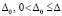, такое, что из неравенства следует 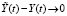, если .

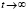Метод Эйлера решения задачи (1)

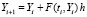, (2)

на произвольном отрезке 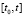применяется в предположении, что значение 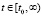является произвольно фиксированным, при этом индекс i неограниченно растет одновременно с убыванием равномерного шага:

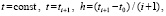
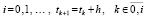. (3)

Используемые в дальнейшем критерии устойчивости вначале приводятся для линейной системы, которую, не умаляя общности, можно считать однородной,

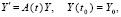(4)

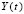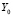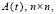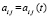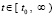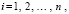
где , определяются так же как для (1), матрица состоит из функций , ; 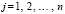. В [6] доказана

Теорема 1. В рассматриваемых условиях решение задачи (4) устойчиво тогда и только тогда, когда

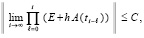(5)

.

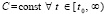Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось (5), а также соотношение

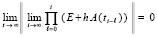. (6)

В (5), (6) E – единичная матрица, h – шаг метода Эйлера решения задачи (4), определяемый на 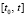согласно (3): 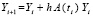. Отсюда

,

.

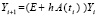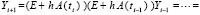
Для линейной системы все решения устойчивы, если устойчиво какое-либо одно решение, все неустойчивы, если неустойчиво хоть одно решение [11]. Из равенства

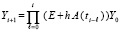
видно, что устойчивость или неустойчивость нулевого решения, а значит, всей системы определяется исключительно асимптотическим поведением предела частичного произведения

,

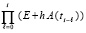то есть

,

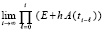что приводит к критериям (5), (6).

Согласование с (3) означает, что в частичном произведении

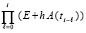
при каждом увеличении числа сомножителей i меняется значение шага 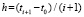, причем одинаково и одновременно в каждом сомножителе:

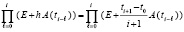. (7)

Свойство (7) шага h сохраняется для частного случая критериев (5), (6), а именно когда в (4) матрица в постоянна: 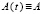. Для такой матрицы коэффициентов 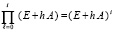. Имеет место

Следствие 1. В случае 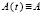система (4) устойчива тогда и только тогда, когда

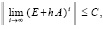(8)

.

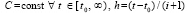Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось (8) и соотношение

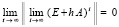. (9)

Нетрудно видеть, что в (8), (9) без изменения результата индекс i можно взять равным целой степени по основанию два: 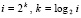. Отсюда вытекает

Следствие 2. В случае 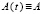система (4) устойчива тогда и только тогда, когда

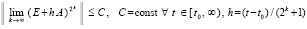. (10)

Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось (10) и соотношение

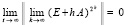. (11)

Аналогично (8), (10), шаг метода Эйлера в (9), (11) – переменная величина, 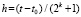. С этой трактовкой критерии (8), (9) и (10), (11) уточняют формулировки прототипов, данные в [5, 6], а также в [7].

Для системы общего вида (1) разность между возмущенным и точным решением с помощью метода Эйлера можно представить в виде [5, 6]

,

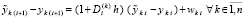где 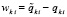– разность остаточных членов формулы Тейлора для k-х компонентов решения,

.

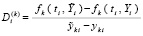Отсюда

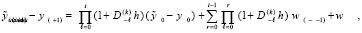
где h из (3), 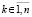. В этом выражении

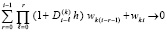
при условии 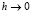, или, что равносильно, 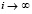. В результате

.

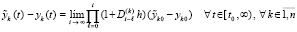В [5, 6] показано, что имеет место

Лемма 1. В рассматриваемых условиях для устойчивости решения задачи (1) необходимо и достаточно, чтобы существовало 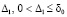, такое, что 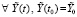, при ограничении 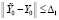выполняется неравенство

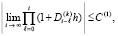
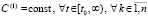. (12)

Для асимптотической устойчивости необходимо и достаточно, чтобы выполнялось предыдущее утверждение и существовало 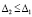, такое, что 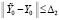влечет

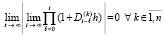. (13)

На 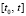частичное произведение

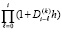
при изменении i меняет одновременно все свои сомножители и h в каждом из них согласно (3). Поскольку

,

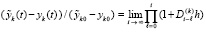
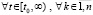то из леммы следует

Теорема 2 [6, 7]. Формулировка и утверждение леммы 1 дословно сохраняются при замене (12) на соотношение

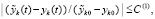
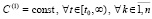, (14)

и (13) – на соотношение

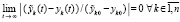. (15)

Частное в (14) и (15) выражает отношение возмущения решения именно к вызвавшему его возмущению начальных значений. При всех их вариациях в границах 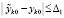выполняется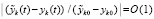 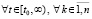, что отличает теорему 2 от определений устойчивости и асимптотической устойчивости.

Именно (14) и (15) используется в дальнейшем. В [7] показано, что эти критерии пригодны в условиях, практически не требующих дополнительных формальных ограничений помимо условий существования и единственности решения задачи (1). В частности, критерии (14), (15) не зависят от метода приближенного решения в границах его сходимости.

Для случая анализа устойчивости нулевого решения системы теорема 2 влечет

Следствие 3. Пусть система (1) имеет нулевое решение . Относительно его устойчивости дословно сохраняются формулировка и утверждение леммы 1 при замене (12) на соотношение

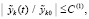
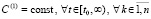, (16)

и (13) – на соотношение

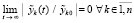. (17)

Значок волны можно убрать, взяв любое решение с ненулевыми начальными значениями из соответственных окрестностей нулевых компонентов.

Пусть автономная система

(18)

где ,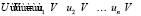

, ,

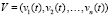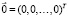имеет нулевое решение с начальными значениями из (18), пусть требуется выполнить анализ устойчивости этого решения (точки покоя). Не умаляя общности, можно считать, что 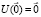. Производная правой части (18) априори, аналитически и инвариантно, вычисляется по формуле производной сложной функции [12]:

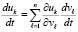, или,

.

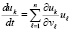В [7] для системы (18) доказаны следующие достаточные условия устойчивости.

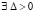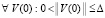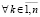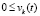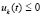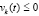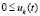
Предложение 1. Если , такое, что , выполняется любая из пар неравенств , или , , 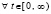то точка покоя системы (18) устойчива.

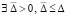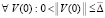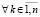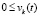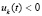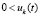
Теорема 3. Пусть выполнены условия предложения 1. Если , такое, что , выполняется пара неравенств , или , , и при этом 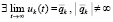, то точка покоя системы (18) асимптотически устойчива.

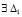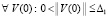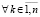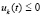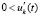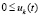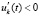
Теорема 4. Если точка покоя системы (18) устойчива и , такое, что , выполнено либо , , либо , , 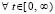то точка покоя асимптотически устойчива.

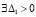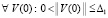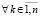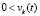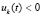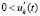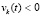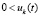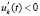
Теорема 5. Если , такое, что , выполняется любая из троек неравенств , , или , , , 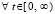то точка покоя системы (18) асимптотически устойчива.

Предложение 2. Пусть 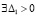, такое, что 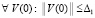, 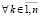задача (18) имеет решения со свойством постоянства знаков компонентов, 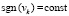, то есть либо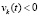 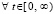, либо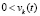 . Пусть 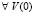из рассматриваемой окрестности начальных данных 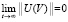. Тогда для асимптотической устойчивости точки покоя необходимо и достаточно выполнение одной из пар неравенств 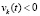, 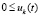или , .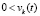

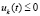
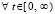Предложение 3. Пусть точка покоя системы (18) устойчива. Тогда для ее асимптотической устойчивости необходимо и достаточно выполнение одной из пар неравенств 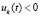, 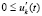или , .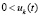

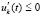
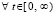Следующие условия достаточны для неустойчивости.

Предложение 4. Если для задачи (18) 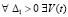: 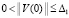, , 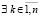, 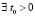такие, что неравенства 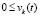, 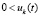верны 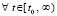, при этом либо 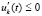, либо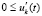 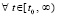, то точка покоя неустойчива. Аналогично, если , .

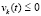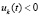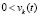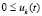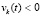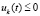
Нетрудно видеть, что к тому же результату приводит выполнение соотношений , или , 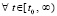при сохранении условий относительно .

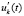Теорема 6. Точка покоя системы (18) неустойчива, если 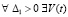: 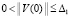, , 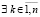, 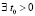такие, что 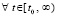верна хоть одна из пар следующих неравенств при сохранении условий предложения 4 относительно 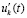: 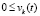, 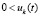; 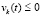, 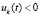; 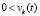, 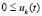; 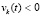, 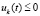. В тех же условиях решение неустойчиво, если верна хоть одна из пар следующих неравенств: , ; , ; , ; , .

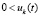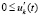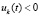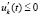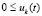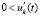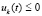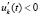Все приведенные критерии применимы для линейной системы с матрицей A постоянных коэффициентов, включая критерии для автономной системы, частным случаем которой является такая система:

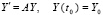. (19)

Для системы (19) каждый из этих критериев достаточно проверить для одного произвольно взятого решения (и, при необходимости, его производных) с начальным вектором из ненулевых координат [7].

Методы, используемые для численного моделирования

Для данной цели фактически пригодны любые методы приближенного решения задачи Коши для ОДУ. Ниже некоторые из них сравниваются между собой относительно достоверности и эффективности численного моделирования устойчивости на их основе. В набор сравниваемых будут входить метод Эйлера (2), метод Рунге – Кутты 4-го порядка, метод Батчера, метод Дормана – Принса. Запись последних с явно заданными числовыми коэффициентами вместе с программной реализацией можно найти, в частности, в [13]. Акцентированное внимание в рассматриваемом применении уделяется кусочно-интерполяционному методу с итерационным уточнением. Как правило, метод используется в версии на основе интерполяционного полинома Ньютона с автоматическим выбором параметров [9]. В дальнейшем, однако, будет рассматриваться упрощенная версия, использующая интерполяционный полином Лагранжа без автоматического выбора параметров [10], которая кратко излагается непосредственно ниже. Полином Лагранжа для интерполируемой функции f(x) на отрезке 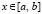строится с равноотстоящими узлами: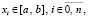 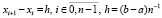. Вводится переменная 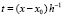. Тогда 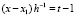, …, , , 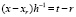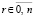полином Лагранжа примет вид [10]

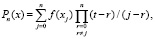
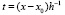. (20)

В (20) 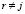– корни полинома .

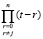По корням восстанавливаются коэффициенты этого полинома с помощью алгоритма [10]:

,

,

,

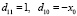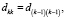
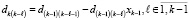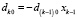где .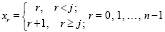

Здесь .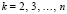

При 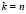восстановятся все искомые коэффициенты и преобразуемый полином примет вид алгебраического полинома с целочисленными коэффициентами:

.

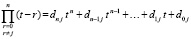Далее, приводятся подобные в (20), и полином Лагранжа примет вид

,

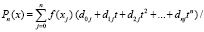
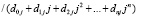где 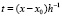, или, при полном приведении подобных,

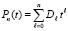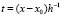, , (21)

где 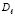– числовые коэффициенты. В дальнейшем приближении 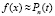выполняется с использованием (21), что влечет приближение производных:

,

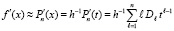t из (21). Кусочная интерполяция основана на том, что весь отрезок интерполяции разбивается на подынтервалы равной длины

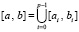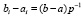, , (22)

и описанное преобразование полинома Лагранжа (20), (21) выполняется на каждом в отдельности подынтервале 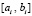. В результате получится

, ,

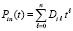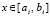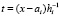, . (23)

Приближение первообразной на каждом подынтервале примет вид:

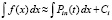, или,

.

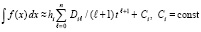Для приближенного решения ОДУ кусочная интерполяция строится следующим образом. Пусть рассматривается задача Коши для уравнения вида

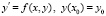, (24)

где функция 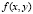определена, непрерывна и удовлетворяет всем условиям существования и единственности на отрезке (22). На каждом подынтервале интерполируется правая часть (24) посредством полинома вида (23). С этой целью в 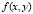подставляется приближенное значение y, на начальном отрезке 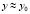. При фиксированных n и k на отрезке 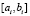, , 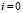затем, аналогично, при 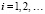, выполняется итерационное уточнение, которое состоит в следующем. Пусть

,

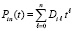тогда 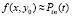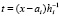, 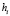– шаг интерполяции на 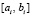. Первообразная

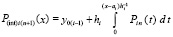
равная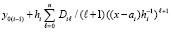

принимается за приближение решения:

, .

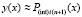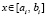Далее, полагается 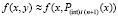, и при том же n, на том же отрезке строится интерполяционный полином вида (23) для приближения полученной функции:

, .

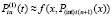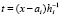От этого полинома снова берется первообразная с тем же значением константы

,

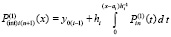подставляется в правую часть,

,

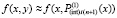которая затем интерполируется аналогично:

.

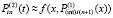Фактически итерации

,

,

,

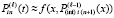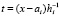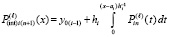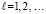
продолжаются до заданной границы 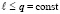. Выше предполагалось, что за значение 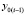принято 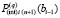. По окончании итераций на 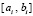выполняется переход к 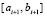, где за значение 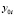принимается . Таким способом проходится весь отрезок 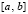из (22). Для иллюстрации метода ниже приводится программная реализация (здесь и ниже Delphi) решения задачи 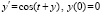, (аналитическое решение ):

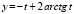ProgramRD_Lag999_dn_N2; {$APPTYPECONSOLE}usesSysUtils, Math;

var kiter,koutput:integer; Npol:byte;tt:longint;Anach,Bkonech,velint,ynach:extended;

function f(x,y: extended):extended; begin f:=cos(x+y) end;

function fun(x:extended):extended; begin fun:=-x+2*arctan(x) end;

procedure RD(y_nach,A_nach,B_konech,vel_int:extended;n:byte;k_iter,k_output:integer;tt_:longint);

const nn=11;type vect=array[-3..nn] of extended; matr=array[0..nn,0..nn] of extended; matr_d=array[0..nn] of matr;

var xx,yy,CC:vect; g:matr; dd,ddint:matr_d; t,a0,b0,h,x,y0,s1:extended; i,r,j,l:integer; kk,m:longint;

procedure podgotovka; var i,j,n:integer; z,d,dint: matr;

procedure ro(n1,j:integer; z:matr; var d:matr); var e:matr; l,k:integer;

begin e[1,1]:=1;e[1,0]:=-z[j,0]; for k :=2 to n1 do begin e[k,k]:=e[k-1,k-1];

for l :=1 to k-1 do e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1]; e[k,0]:=-e[k-1,0]*z[j,k-1]; end;

for l:=n1 downto 0 do d[j,l]:= e[n1,l]; end;

function gorner1(n,j:integer;Mcoef:matr):extended; var s:extended; i:integer;

begin s:=Mcoef[j,n]; for i:=n-1 downto 0 do s:=s*j+Mcoef[j,i]; gorner1:=s;end;

begin for j:=0 to nn do for i:=0 to nn-1 do if i<j then z[j,i]:=i else z[j,i]:=i+1;

for n:=1 to nn do for j:=0 to n do ro(n,j,z,dd[n]); for n:=1 to nn do for j:=0 to n do g[n,j]:= gorner1(n,j,dd[n]) end;

function gorner (Mcoef: vect; x:extended):extended; var s,t:extended; i,n:byte;

begin t:=(x-Mcoef[-1])/Mcoef[-2]; n:=trunc(Mcoef[-3]); s:=Mcoef[n];

for i:=n-1 downto 0 do s:=s*t+Mcoef[i]; gorner:=s; end;

procedure Polynomial(x:vect;h,y0:extended;n,K_it:integer; var C:vect); var i,j,r,iter:integer; sk,t:extended; fy,y,dn:vect;

begin y[0]:=y0; for r:=1 to n do y[r]:=y0; for iter:=1 to K_it do begin for r:=0 to n do fy[r]:=f(x[r],y[r]);

for i:=0 to n do begin sk:=0; for j:=0 to n do sk:=sk+fy[j]*dd[n][j,i]/g[n,j]; dn[i]:=sk; end;

C[0]:=y[0]; C[-1]:=x[0]; C[-2]:=h; C[-3]:=n+1;

for i:=1 to n+1 do C[i]:=dn[i-1]*h/i; for i:=1 to n do y[i]:=gorner(C,x[i]); end; end;

beginpodgotovka; writeln(‘x’:4,’y’:15,’Pogr’:25); writeln; a0:=A_nach; b0:=a0+vel_int; y0:=y_nach;xx[0]:=a0; kk:=0;

while a0 <= B_konech-vel_int/2 do begin h:=(b0-a0)/n; for i:=1 to n+1 do xx[i]:=a0+i*h;

Polynomial(xx,h,y0,n,k_iter,CC); kk:=kk+1;if kk=tt_ then begin for l:=1 to k_output do begin

x:=a0+l*(b0-a0)/k_output; writeln(x:7:6,’ ‘, gorner(CC,x),’ ‘,abs(gorner(CC,x)-fun(x))); end; writeln; kk:=0; end;

y0:=gorner(CC,xx[n]); xx[0]:=xx[n]; a0:=a0+vel_int; b0:=a0+vel_int; end; end;

Begin Anach:=0; Bkonech:=512; ynach:=0; velint:=0.02; Npol:=5; kiter:=10; tt:=256; koutput:=1;

RD(ynach,Anach,Bkonech,velint,Npol,kiter,koutput,tt); readln; end.

Результат работы программы на отрезке [a, b] = [0, 512], (Δy – абсолютная погрешность):

t y Δy

5.12 -2.36417597092616E+0000 0.0E+0000

10.24 -7.29310249338465E+0000 8.7E-0019

…… ………………………… …………

256.00 -2.52866219806674E+0002 2.8E-0017

261.12 -2.57986066622692E+0002 1.9E-0016

…… ………………………… …………

506.88 -5.03742353048362E+0002 3.9E-0016

512.00 -5.08862313591443E+0002 6.1E-0016

Здесь n = 5, где 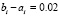, k = 0, q = 10, где q – число итераций. Результаты близки, хотя несколько уступают в точности результатам кусочной интерполяции на основе полинома Ньютона, те и другие реализуются с меньшей абсолютной погрешностью решения задачи Коши, чем известные разностные методы [10].

Одна из целей излагаемой работы – показать, что кусочно-интерполяционный метод на основе представленных выше критериев позволяет эффективно и достоверно определять устойчивость по ходу решения ОДУ.

О параметрах численного эксперимента по сравнению приближенных методов при моделировании устойчивости решения ОДУ. В процессе программной реализации все разностные методы применяются с одним и тем же равномерным шагом 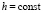, при этом формально нарушается условие 4, согласно которому шаг должен стремиться к нулю на каждом отрезке приближенного решения. В частности, это нарушение относится к линейным системам с постоянными коэффициентами, устойчивость которых анализируется на основе критериев (10), (11). В последнем случае возникает парадокс: заложенное в критерий видоизменение метода Эйлера позволяет достигать точки независимой переменной порядка 109 с достоверной оценкой устойчивости, что на практике не улучшается никакими другими методами. Это объясняется сокращением количества вычислительных операций в (10), (11) до логарифмического от исходного числа операций разностных методов. В результате ограничивается накопление погрешности и повышается достоверность оценки устойчивости.

Численное моделирование устойчивости линейной системы с постоянной матрицей коэффициентов. Применение критериев (10), (11) иллюстрируется на примере оценки устойчивости системы

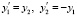, (25)

или

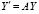, (26)

где .

Программа, реализующая (10), (11) примет вид

Program USTlinconstDU2222; {$APPTYPE CONSOLE} uses SysUtils;

const n=2; h=1.1e-14;

type matr=array[1..n,1..n] of extended; vect=array[1..n] of extended;

const A: matr= (( 0, 1),

(-1, 0));

{ (( -10, -5),

(5, -10)); }

{ ((3, -1, 1),

(-1, 5,-1),

(1, -1, 3)); }

var a1,c: matr; s0,s1,x: extended; i,j,l,k: integer;

procedure ummatr (var a1,c: matr);

var s1: extended; i,j,l : integer;

begin for i := 1 to n do for j := 1 to n do

begin s1:=0; for l:= 1 to n do s1:= s1+a1[i,l]*a1[l,j]; c[i,j]:= s1

end; end;

begin for i:=1 to n do for j:=1 to n do

begin a1[i,j]:=a[i,j]*h; if i=j then a1[i,j]:=a1[i,j]+1 end;

k:=0; while abs(x) <= 0.83e9 do begin

ummatr (a1,c); k:=k+1; x:=h*exp((k+1)*ln(2));

for i:=1 to n do for j:=1 to n do a1[i,j]:=c[i,j]; s0:=0; for i:=1 to n do

for j:=1 to n do s0:=s0+sqr(a1[i,j]); s0:= sqrt(s0); write (‘ ‘:2, s0:2,’ ‘:8); end; writeln;

writeln; writeln (‘ ‘:2, ‘h =’,h,’ ‘); writeln (‘ ‘:2, ‘k=’,k,’ ‘);writeln (‘ ‘:2, ‘x=’,x:2,’ ‘); readln

end.

Результат работы программы:

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

………………………………………………………………………………………………….

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

h = 1.10000000000000E-0014

k =75

x = 8.3E+0008

С шагом 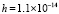выполнено 75 итераций, достигнуто значение 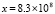, и на всем этом отрезке округленное значение эвклидовой нормы матрицы 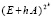при каждом значении k не превосходит значения 1.4. Согласно (10) это указывает на неасимптотическую устойчивость системы. В процессе анализа системы вида (26) можно получить дополнительное подтверждение устойчивости следующим образом. Начиная от 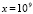можно приближенно решить систему, например, методом Эйлера при любых начальных значениях с ненулевыми компонентами. Отрезок решения можно взять сравнительно небольшо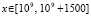й: или 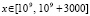. Если на этих отрезках решение сохранит ограниченность, то с учетом результатов работы программы USTlinconstDU2222, с высокой степенью вероятности решение устойчиво. Соответственно устойчива вся система (26) [11]. Так, в случае системы (25), при начальных значениях 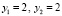, с шагом 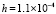, метод Эйлера покажет ограниченность компонентов значениями 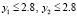. Примеры анализа с помощью критериев (10), (11) устойчивости, асимптотической устойчивости и неустойчивости для различных матриц более высокой размерности приводятся в [7]. Примеры, непосредственно доступные в данной программе, закомментированы в разделе описания констант и обсуждаются ниже.

В общем случае, для подтверждения устойчивости, оцениваемой по критериям (10), (11), можно дополнительно проверить ограниченность решения на отрезке, левая граница которого является произвольно большим числом. Начальные значения с ненулевыми компонентами можно задать произвольно, длину проверочного отрезка можно произвольно увеличить. Если приближенное решение ограничено, то система устойчива [11].

Если согласно (11) система асимптотически устойчива, то программная реализация этого критерия будет иметь результатом неограниченно убывающее значение нормы. Так, по той же программе Program USTlinconstDU2222 в случае матрицы

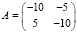системы (26) получится

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

……………………………………………………………………………………………............

1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000 1.4E+0000

1.4E+0000 1.4E+0000 1.3E+0000 1.3E+0000 1.1E+0000 8.7E-0001 5.4E-0001

2.0E-0001 2.9E-0002 6.1E-0004 2.7E-0007 5.1E-0014 1.8E-0027 2.3E-0054

3.8E-0108 1.0E-0215 7.2E-0431 3.6E-0861 9.3E-1722 0.0E+0000 0.0E+0000

……………………………………………………………………………………………………

0.0E+0000 0.0E+0000 0.0E+0000 0.0E+0000

h = 1.10000000000000E-0014

k = 75

x = 8.3E+0008

Если же система (26) неустойчива, то программа обнаружит неограниченный рост нормы, что может повлечь переполнение. Чтобы увидеть характер роста нормы, следует сократить отрезок приближения до длины, например, 3000. Так, для матрицы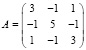

системы (26) та же программа (при n = 3) выдаст переполнение. Однако при сокращении отрезка решения путем замены оператора while abs(x) <= 0.83e9 do на оператор while abs(x) <= 0.83e3 do программа выдаст результат с характерным ростом нормы:

1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000

1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000 1.7E+0000

…………………………………………………………………………………………………

1.7E+0000 1.7E+0000 1.7E+0000 1.8E+0000 1.8E+0000 1.8E+0000 1.9E+0000

2.1E+0000 2.5E+0000 3.9E+0000 1.0E+0001 1.0E+0002 1.0E+0004 1.1E+0008

1.3E+0016 1.9E+0032 3.5E+0064 1.2E+0129 1.5E+0258 2.3E+0516 5.1E+1032

2.6E+2065

h = 1.10000000000000E-0014

k = 56

x = 1.6E+0003

Необходимо отметить, что длина отрезка, на котором выполняется описанное моделирование устойчивости системы вида (26), сокращается с ростом размерности системы, соответствующие данные приводятся в [7].

Численное моделирование устойчивости линейной системы с переменной матрицей коэффициентов. В случае задачи (4) с переменной матрицей 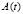большой длины отрезка приближенного решения достигнуть затруднительно, поскольку применение критериев (5), (6) исключает пропуск промежуточных шагов (как это имело место в случае применения (10), (11)). Критерий реализуется непосредственно как частичное произведение

.

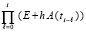Если выбрать малый шаг разностного метода, существенно возрастет время решения, при увеличении шага накапливается погрешность. То и другое препятствует выбору отрезка моделирования большой длины. Так, если для анализа устойчивости системы

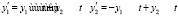(27)

выбрать шаг 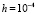, то результат применения критериев (5), (6) (за время ≈24 сек) можно увидеть на отрезке 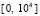(округленная норма дана в конце каждого отрезка длины 100):

1.6E+0000 2.4E+0000 3.8E+0000 6.5E+0000 8.8E+0000 7.7E+0000 8.6E+0000 6.0E+0000 3.5E+0000

2.2E+0000 1.5E+0000 1.1E+0000 1.7E+0000 2.5E+0000 4.2E+0000 7.0E+0000 8.9E+0000 8.2E+0000

……………………………………………………………………………………………………………...

3.5E+0000 2.2E+0000 1.5E+0000 1.1E+0000 1.7E+0000 2.5E+0000 4.2E+0000 7.0E+0000 8.9E+0000

8.2E+0000 8.3E+0000 5.5E+0000 3.2E+0000 2.0E+0000 1.4E+0000 1.2E+0000 1.8E+0000 2.7E+0000

4.6E+0000 7.5E+0000 8.8E+0000

В этом случае

,

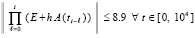что согласно (5) указывает на устойчивость (в границах данного приближения к асимптотике). Аналогично, для системы

получится

3.7E-0044 1.4E-0087 5.1E-0131 1.9E-0174 7.0E-0218 2.6E-0261 9.5E-0305 3.5E-0348 1.3E-0391

……………………………………………………………………………………………………

2.0E-3996 7.2E-4040 2.7E-4083 9.9E-4127 3.7E-4170 1.4E-4213 5.0E-4257 1.9E-4300 6.9E-4344

В этом случае в численном приближении выполняется

,

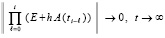что согласно (6) указывает на асимптотическую устойчивость (в границах приближения к асимптотике).

В случае линейных систем вида (4) целесообразно применить прием дополнительной проверки «асимптотического» поведения решения на произвольно удаленном отрезке, как это описано выше для систем вида (26).

Численное моделирование устойчивости нелинейной системы

Вначале численные эксперименты выполнены на отрезке или на промежутке длины 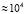, величина возмущения начальных значений всегда полагается равной 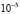. Как отмечалось, при использовании разностных методов принят одинаковый шаг 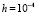. Метод кусочно-интерполяционного приближения с итерационным уточнением применяется с фиксированными значениями n и k, указываемыми для каждой задачи, первоначально, n = 2, k = 5.

Прежде чем выполнять сравнение методов, необходимо оговорить особенность критериев (14), (15) и (16), (17). Именно лемма 1, теорема 2 и следствие 3 предполагают наличие достаточно малой окрестности возмущения начальных значений (это не требовалось в линейном случае). В то же время при каждом численном приближении задается одно и только одно начальное значение. Пусть, например, требуется исследовать на устойчивость нулевое решение системы

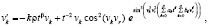
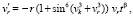
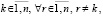(28)

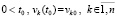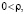
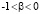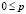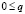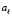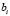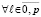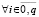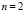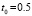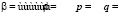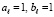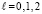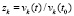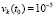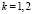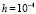где , ; , ; , – вещественные числа , для значений , , , , . На основе (16), (17), , приводимая ниже программа, , , , метод Эйлера, , даст соответственный признак.

program USTnelinPRIMERBULANOV;{$APPTYPE CONSOLE} uses SysUtils;

const h = 0.0001; tt=100000; var x,y1,y2,y10,y20,z1,z2,eps1,eps2: extended; k: longint;

function f1(x,y1,y2:extended):extended;

begin f1:=-1/2*y1/sqrt(x)+1/sqr(x)*y1*sqr(cos(y1*y2))*

exp(sin(sqr(y1)*y1*sqr(y2)*(1+x+sqr(x)+x*sqr(x))*(1+y2+sqr(y2)+sqr(y2)*y2))*

sqr(sin(sqr(y1)*y1*sqr(y2)*(1+x+sqr(x)+x*sqr(x))*(1+y2+sqr(y2)+sqr(y2)*y2)))) end;

function f2(x,y1,y2:extended):extended;

begin f2:=- 2/sqrt(x)*y2*(1+ sqr(sqr(sin(sqr(y1)*y1+sqr(y2)*y2)))*

sqr(sin(sqr(y1)*y1+sqr(y2)*y2))) end;

begin

k := 0; eps1:=0.00001{e-10}{e-1}{*10}{*2}; eps2:=0.00001{e-10}{e-1}{*10}{*2};

y1:= 0.0; y10 := y1+{-}eps1; y2 :=0.0; y20 := y2+{-}eps2; x:=0.5; while x <=10000 do

begin

y10 := y10 + h * f1(x,y10,y20); y20 := y20 + h * f2(x,y10,y20);

z1:=abs(y10/eps1); z2:=abs(y20/eps2); k:=k+1; if k = tt then

begin writeln (‘x=’,x:4,’ ‘); writeln (‘z1=’,z1:4,’ ‘,’z2=’,z2:4,’ ‘,’norma=’,sqrt(sqr(z1)+sqr(z2)) :4);

k:=0 end; x:=x+h; end; readln

end.

Результат работы программы:

x= 1.0E+0001 z1= 5.3E-0001 z2= 4.0E-0005 norma= 5.3E-0001

x= 2.0E+0001 z1= 1.5E-0001 z2= 2.3E-0007 norma= 1.5E-0001

……………………………………………………………………......

x= 5.5E+0002 z1= 1.2E-0009 z2= 6.9E-0040 norma= 1.2E-0009

x= 5.5E+0002 z1= 9.7E-0010 z2= 2.9E-0040 norma= 9.7E-0010

……………………………………………………………………......

x= 3.1E+0003 z1= 1.2E-0023 z2= 9.3E-0096 norma= 1.3E-0023

x= 3.1E+0003 z1= 1.1E-0023 z2= 6.5E-0096 norma= 1.2E-0023

……………………………………………………………………......

x= 1.0E+0004 z1= 6.1E-0043 z2= 4.8E-0173 norma= 6.1E-0043

x= 1.0E+0004 z1= 5.8E-0043 z2= 3.9E-0173 norma= 5.8E-0043

Эвклидова норма отношения 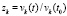, 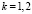убывает до 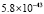, что согласно (17) указывает на асимптотическую устойчивость нулевого решения. Формально такое поведение нормы должно выполняться в некоторой окрестности нулевых начальных значений, а не только при одном из них. Поэтому на практике требуется повторить выполнение программы при других достаточно малых начальных значениях, чтобы проверить достоверность вывода об асимптотической устойчивости. В программе закомментированы различные возмущения начальных значений, в том числе со сменой знака возмущения, при которых приведенные данные повторяются с точностью до коэффициента. В результате на основании численного эксперимента можно сделать достаточно достоверный вывод об асимптотической устойчивости нулевого решения. Формальная проверка в различных точках Δ-окрестности начального вектора необходима для компьютерного анализа только в случае нелинейной системы. С целью минимизации временной сложности анализ можно выполнять на параллельной вычислительной системе одновременно по всем проверочным начальным значениям и по всем уравнениям системы.

Тот факт, что проверка по одному начальному значению дает одинаковый результат с проверкой по нескольким начальным значениям из достаточно малой окрестности возмущения начального вектора отвечает непрерывной зависимости решения от начальных значений. Однако непрерывная зависимость численно моделируется на конечном отрезке решения, поэтому проверка по нескольким начальным значениям не только необходима сама по себе, но ее следует выполнять на отрезках решения различной длины.

Непосредственно для сравнения методов будет использоваться только один вектор начальных значений. Для разностных методов условия сравнения будут одинаковы в соответствии указанным выше параметрам.

Пусть требуется выполнить анализ устойчивости нулевого решения системы (27). Результаты численного моделирования и время работы каждого метода на основе критерия (16) приводятся в табл. 1. В первом столбце таблицы указано значение независимой переменной. Во втором – округленное значение нормы критерия (16), вычисленное на основе решения системы по методу Эйлера, в третьем – на основе решения по методу Рунге – Кутты 4-го порядка, в четвертом – на основе метода Батчера 6-го порядка, в пятом – на основе метода Дормана – Принса 8-го порядка. В шестом столбце таблицы – значение нормы критерия (16), вычисленное на основе решения системы (27) с помощью кусочно-интерполяционного метода с интерполяцией по Лагранжу при значениях параметров n = 2 (степень интерполяционного полинома на подынтервале), k = 5 (2k подынтервалов на каждом отрезке приближенного решения системы длиной 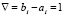). Внизу приводится время работы программы.

Все методы указывают на неасимптотическую устойчивость системы (27), при этом чуть менее точен в оценке метод Эйлера. Кусочно-интерполяционный метод в данном случае оказывается наиболее быстродействующим: он в 8 раз быстрее метода Эйлера, в 34 раза быстрее метода Рунге – Кутты, в 62 раза быстрее метода Батчера и в 113 раз быстрее метода Дормана – Принса, не уступая трем последним в точности.

Таблица 1

Результаты численного моделирования устойчивости системы (27) на основе критерия (16)

Таблица 2

Результаты численного моделирования устойчивости решения системы (29) на основе критерия (14)

Таблица 3

Результаты численного моделирования устойчивости нулевого решения системы (30) на основе критерия (16)

Пусть требуется выполнить анализ устойчивости решения задачи

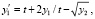
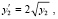
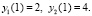(29)

Численное моделирование выполняется при тех же значениях длины отрезка, шага и величины возмущения, что и в случае системы (27).

Каждый столбец табл. 2, начиная со второго, содержит построчно совпадающие значения нормы критерия (16). В частности, второй из них содержит значения (сверху вниз): 7.5 E+0005, 3.0 E+0006, 6.8 E+0006, 1.2 E+0007, 1.9 E+0007, 2.7 E+0007, 3.7 E+0007, 4.8 E+0007, 6.1 E+0007, 7.5 E+0007. Методы одинаково указывают на неустойчивость решения задачи (29), что соответствует виду общего решения [9]. Кусочно-интерполяционный метод при данных параметрах в 5 раз быстрее метода Эйлера, почти в 15 раз быстрее метода Рунге – Кутты, в 40 раз быстрее метода Батчера и в 72 раза быстрее метода Дормана – Принса.

Пусть требуется выполнить анализ устойчивости нулевого решения задачи Коши

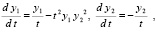
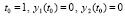. (30)

Результаты анализа приводятся в табл. 3, все численные методы взяты с теми же параметрами, которые использовались при построении табл. 2.

Каждый столбец табл. 3, начиная со второго, содержит одинаковые значения нормы критерия (16). В частности, второй из них содержит значения (сверху вниз): 1.0 E+0003, 2.0 E+0003, 3.0 E+0003, 4.0 E+0003, 5.0 E+0003, 6.0 E+0003, 7.0 E+0003, 8.0 E+0003, 9.0 E+0003, 1.0 E+0004. Методы одинаково указывают на неустойчивость нулевого решения задачи (30), что соответствует аналитической оценке, данной в [11]. Кусочно-интерполяционный метод в этом случае в 5 раз быстрее метода Эйлера, в 14 раз быстрее метода Рунге – Кутты, в 34 раза быстрее метода Батчера, в 66 раз быстрее метода Дормана – Принса.

Замечание 1. Задача (30) дана в [11] как пример того, что решение стремится к нулю, но неустойчиво. В этом случае

,

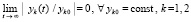и формально неустойчивость может обнаруживаться только на множестве точек Δ-окрестности, в которой должно выполняться (16). Поэтому, несмотря на рост нормы в табл. 3, более полное исследование должно выявить аналогичный рост не для одного вектора начальных значений, а для конечного множества начальных векторов из Δ-окрестности нулевого начального вектора, причем на отрезках 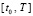произвольной длины. Экспериментально искомое множество начальных значений извлекается как конечная подпоследовательность соотношения 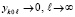, при этом достаточно выбирать только монотонно убывающие начальные значения.

Замечание 2. Приведенные данные не означают, что кусочно-интерполяционный метод во всех случаях превосходит по быстродействию все разностные методы. Сравнение относится только к данной в таблицах выборке шага и других параметров. При иных выборках это может оказаться не так, в частности, для методов с большим шагом, например, 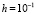, те же разностные методы окажутся более быстрыми, чем кусочно-интерполяционный.

Проводился сравнительно обширный численный эксперимент, который показал, что данные табл. 1–3 не случайны. Как правило, во всех рассматривавшихся случаях все численные методы, представленные в этих таблицах, показывали совпадающие значения норм при равных параметрах для одинаковой системы на отрезках приближенного решения равной длины. По крайней мере, такая статистика сохранялась для систем из двух уравнений. Нарушения этой закономерности встречались скорее как исключения. Так, в частности, для линейной системы из шести уравнений

,

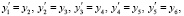
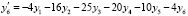на 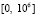с помощью метода Эйлера (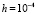) получались значения норм (16), (17):

;

;

;…;

;

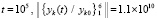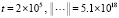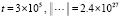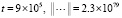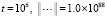
(время выполнения программы 18 мин. 48 сек.). Аналогичный, но менее бурный рост нормы метод Эйлера проявлял и при :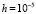

;

;

;

;

.

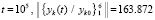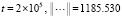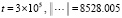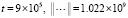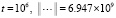Такой рост нормы противоречит показанной в [12] неасимптотической устойчивости рассматриваемой линейной системы. В то же время кусочно-интерполяционный метод с итерационным уточнением (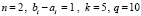) на 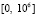давал правильный результат с ограниченной нормой, который в соответствии критериям (16), (17), указывал на неасимптотическую устойчивость данной системы:

;

;

; …;

;

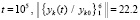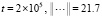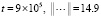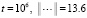
(время выполнения программы 4 мин 6 с). Правильные границы нормы предложенный метод сохранял и на отрезке , аналогичные границы получались, в частности, при .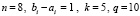

Метод Рунге – Кутты для этой системы при 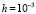давал правильные границы нормы, но за время вдвое большее, чем кусочно-интерполяционный метод. На отрезках меньшей длины все разностные методы приводили к правильным оценкам устойчивости, метод Эйлера для рассматриваемой системы на 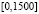показывал именно неасимптотическую устойчивость [7]. С ростом длины отрезка разностные методы могут накапливать погрешность, которая приводит к неадекватной оценке устойчивости на их основе.

С одной стороны, кусочно-интерполяционный метод с итерационным уточнением (без автоматического выбора параметров) на приведенных выше эвристических примерах превосходит разностные методы по точности решения задачи Коши и обладает меньшей временной сложностью, в том числе на отрезках приближения сравнительно большой длины. С другой стороны, этот метод инвариантно дает правильное значение нормы в соответствии с критериями (14)–(17) и может рассматриваться в качестве предпочтительного метода компьютерного анализа устойчивости в реальном времени по ходу решения системы ОДУ. Представленный метод построен на основе интерполяционного полинома Лагранжа. Согласно численному эксперименту его прототип [9, 10], кусочно-интерполяционный метод, построенный на основе интерполяционного полинома Ньютона, является столь же быстродействующим, а по точности иногда выше примерно на один десятичный порядок, поэтому в рассматриваемом применении прототип может оказаться более предпочтительным, чем аналог на основе полинома Лагранжа. Тем не менее практический выбор определяется классом задач, на которых равная точность может достигаться с меньшей степенью полинома Лагранжа. В частности, в табл. 1–3 степень полинома 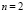, что и определило быстродействие метода.

Моделирование устойчивости на основе знаков решения и двух его производных

Здесь рассматривается программная реализация достаточных условий устойчивости и неустойчивости из предложений 1–4 и теорем 3–6. Алгоритмизация и программирование критериев вначале поясняются на простом примере. Пусть исследуется на устойчивость линейное уравнение

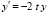. (31)

Первую производную решения задает функция правой части. Вторая – универсально получается из формулы, приведенной при рассмотрении системы (18), где она записывалась в виде

.

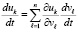В случае уравнения (31) 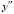можно найти непосредственным дифференцированием правой части. Получится 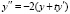, с учетом (31) 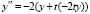, или 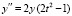. Остается наряду с приближенным решением y выводить приближение первой производной –2ty и приближение второй производной 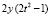. В данном примере можно не прибегать к программной реализации: очевидно, что y противоположно по знаку –2ty и совпадает по знаку с 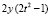для всех 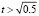. По теореме 5 это означает асимптотическую устойчивость линейного уравнения (31). Оценка соответствует общему решению 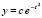, где c – произвольная постоянная. Для иллюстрации общего случая приводится программа и результат ее работы. Вследствие линейности уравнения достаточно проверить одно любое решение с ненулевым начальным значением [7, 11].

program USTnelinznaki;{$APPTYPE CONSOLE} uses SysUtils;

const h = 0.0001; tt=1000000; var x,y,eps: extended; k: longint;

function f(x,y:extended):extended;

begin f:=-2*x*y; end;

function f1(x,y:extended):extended;

begin f1:=2*y*(2*sqr(x)-1); end;

begin

k := 0; eps:=0.00005; y:= eps; x:=0; while x <=10000 do begin

y:= y+h * f(x,y); k:=k+1; if k = tt then begin

writeln(‘x=’,x:4,’ ‘);writeln; writeln(‘ ‘,’norma=’,abs(y/eps));writeln;

writeln(‘y=’,y:4,’ ‘,’f=’,f(x,y):4,’ ‘,’f1=’,f1(x,y):4); writeln; k:=0 end; x:=x+h; end; readln

end.

Результат работы программы:

x= 1.0E+0002 norma= 6.5E-4373 y= 3.3E-4377 f=-6.5E-4375 f1= 1.3E-4372

x= 2.0E+0002 norma= 8.7E-4946 y= 4.4E-4950 f=-1.7E-4947 f1= 7.0E-4945

…………………………………………………………………………………

x= 8.0E+0002 norma= 2.2E-4946 y= 1.0E-4950 f=-1.7E-4947 f1= 2.8E-4944

x= 9.0E+0002 norma= 1.5E-4946 y= 7.3E-4951 f=-1.3E-4947 f1= 2.4E-4944

………………………………………………………………………………….

x= 2.4E+0003 norma= 7. 3E-4947 y= 3.6E-4951 f=-1.7E-4947 f1= 8.4E-4944

x= 2.5E+0003 norma= 0.0E+0000 y= 0.0E+0000 f=-0.0E+0000 f1= 0.0E+0000

…………………………………………………………………………………...

x= 9.9E+0003 norma= 0.0E+0000 y= 0.0E+0000 f=-0.0E+0000 f1= 0.0E+0000

x= 1.0E+0004 norma= 0.0E+0000 y= 0.0E+0000 f=-0.0E+0000 f1= 0.0E+0000

После значения независимой переменной выводится норма (в данном случае – модуль) в соответствии с критериями (16), (17), она убывает до нуля, что указывает на асимптотическую устойчивость уравнения. Вместе с тем знаки y, f, f1 чередуются как +, -, +, что по теореме 5 также указывает на асимптотическую устойчивость.

Замечание 3. В [7] предложения 1–4 и теоремы 3–6 доказаны для случая автономной системы, там же приводятся рассуждения, показывающие, что эти критерии и их доказательства переносятся на случай системы (28). Повторение этих рассуждений влечет применимость рассмотренных критериев также и для уравнения (31).

В случае системы (28) вывод приближенных значений компонентов решения и их производных (правых частей системы) влечет следующие результаты работы программы USTnelinPRIMERBULANOV, которая соответственно модифицируется во фрагменте вывода:

x= 1.0E+0001 y1= 5.3E-0006 f1=-7.7E-0007 y2= 4.0E-0010 f2=-2.5E-0010

x= 2.0E+0001 y1= 1.5E-0006 f1=-1.7E-0007 y2= 2.3E-0012 f2=-1.0E-0012

………………………………………………………………………………..

x= 8.3E+0002 y1= 4.6E-0017 f1=-7.9E-0019 y2= 1.5E-0054 f2=-1.0E-0055

x= 8.4E+0002 y1= 3.8E-0017 f1=-6.6E-0019 y2= 7.3E-0055 f2=-5.0E-0056

………………………………………………………………………………..

x= 1.0E+0004 y1= 6.1E-0048 f1=-3.1E-0050 y2= 4.8E-0178 f2=-9.6E-0180

x= 1.0E+0004 y1= 5.8E-0048 f1=-2.9E-0050 y2= 3.9E-0178 f2=-7.8E-0180

Каждый компонент решения и его производная имеют противоположные знаки +, - на всем отрезке решения. На основании теоремы 3, равно как на основании предложения 2, нулевое решение системы (28) асимптотически устойчиво.

Теорема 3 дает достаточные условия устойчивости. Если они не выполняются, это не означает, что решение не обладает асимптотической устойчивостью. Пусть, например, рассматривается следующая система вида (18):

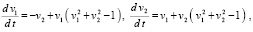(32)

и требуется исследовать на устойчивость ее нулевое решение. Производные каждого компонента будут иметь вид

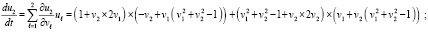
или

.

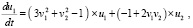
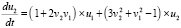Следующая программа выполняет анализ на основании критериев (16), (17), а также выводит знаки компонентов решения и их двух производных.

program ZNAKINELINPRIMER3333; {$APPTYPE CONSOLE} uses SysUtils;

const h = 0.0001; xn=10000; tt=100000; var x,y1,y2,y10,y20,z1,z2,eps1,eps2: extended; k: longint;

function f1(x,y1,y2:extended):extended;

begin f1:=-y2+y1*(sqr(y1)+sqr(y2)-1); end;

function f2(x,y1,y2:extended):extended;

begin f2:=y1+y2*(sqr(y1)+sqr(y2)-1); end;

function f11(x,y1,y2:extended):extended;

begin f11:=(3*sqr(y1)+sqr(y2)-1)*f1(x,y1,y2)+(-1+2*y1*y2)*f2(x,y1,y2); end;

function f21(x,y1,y2:extended):extended;

begin f21:=(1+2*y1*y2)*f1(x,y1,y2)+(3*sqr(y2)+sqr(y1)-1)*f2(x,y1,y2); end;

begin

k := 0; eps1:=1e-5; eps2:=1e-5; y1:= eps1; y2 := eps2; x:=0; while x <=xn do begin

y1 := y1 + h * f1(x,y1,y2); y2 := y2 + h * f2(x,y1,y2); k:=k+1; if k = tt then

begin z1:=y1/eps1; z2:=y2/eps2; writeln(‘x=’,x:4,’ ‘,’norma=’,sqrt(sqr(z1)+sqr(z2)):4);

writeln(‘y1=’,y1:4,’ ‘,’f1=’,f1(x,y1,y2):4,’ ‘,’f11=’,f11(x,y1,y2):4);

writeln(‘y2=’,y2:4,’ ‘,’f2=’,f2(x,y1,y2):4,’ ‘,’f21=’,f21(x,y1,y2):4);writeln;

k:=0 end; x:=x+h; end; readln

end.

Результат работы программы:

x= 1.0E+0001 norma= 6.4E-0005

y1=-1.3E-0010 f1= 7.6E-0010 f11=-1.2E-0009

y2=-6.3E-0010 f2= 4.9E-0010 f21= 2.7E-0010

x= 2.0E+0001 norma= 2.9E-0009

y1=-1.0E-0014 f1=-1.7E-0014 f11= 5.4E-0014

y2= 2.7E-0014 f2=-3.8E-0014 f21= 2.1E-0014

………………………………………………

x= 4.2E+0002 norma= 5.5E-0183

y1= 5.4E-0188 f1=-4.5E-0188 f11=-1.8E-0188

y2=-9.1E-0189 f2= 6.3E-0188 f21=-1.0E-0187

x= 4.3E+0002 norma= 2.5E-0187

y1=-2.3E-0192 f1= 3.3E-0192 f11=-2.0E-0192

y2=-9.9E-0193 f2=-1.2E-0192 f21= 4.6E-0192

………………………………………………..

x= 1.0E+0004 norma= 0.0E+0000

y1= 1.1E-4344 f1=-3.0E-4344 f11= 3.7E-4344

y2= 1.8E-4344 f2=-7.1E-4345 f21=-2.2E-4344

x= 1.0E+0004 norma= 0.0E+0000

y1= 2.5E-4350 f1= 9.5E-4349 f11=-1.9E-4348

y2=-9.7E-4349 f2= 1.0E-4348 f21=-4.9E-4350

Эвклидова норма 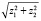отношений 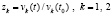(в программе z1:=y1/eps1; z2:=y2/eps2; writeln (‘x=’,x:4,’ ‘,’norma=’, sqrt(sqr(z1)+sqr(z2)):4);) составлена для возмущенного решения. Эта норма убывает к нулю, что в соответствии с критериями (16), (17) необходимо и достаточно для асимптотической устойчивости нулевого решения системы (32). В то же время знаки y, f, f1 иногда чередуются как +, -, +, иногда как -, +, - , иногда как +, +, - или -, -, +, но иногда как +, -, - или -, +, +, что в совокупности не является достаточными условиями асимптотической устойчивости в границах рассматриваемых знаковых критериев (результат сохраняется для всех закомментированных возмущений нулевого начального вектора). Таким образом, асимптотическая устойчивость нулевого решения имеет место согласно необходимым и достаточным условиям критериев (16), (17), и это соответствует аналитическим оценкам, приведенным в [14], тогда как достаточные условия предложений 1–4 и теорем 3–6 асимптотической устойчивости не показывают.

Напротив, практический пример достаточности условий неустойчивости теоремы 6 иллюстрирует нулевое решение задачи (30). Для соответствия обозначений задачу можно записать в виде

,

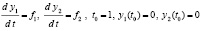где .

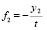Производные правых частей примут вид

,

,

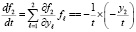или

, .

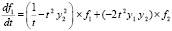Программная реализация примет вид

program ZNAKINELINPRIMER4444; {$APPTYPE CONSOLE} uses SysUtils;

const h = 0.0001; xn=10000; tt=100000; var x,y1,y2,y10,y20,z1,z2,eps1,eps2: extended; k: longint;

function f1(x,y1,y2:extended):extended;

begin f1:=y1/x-(sqr(x))*y1*sqr(y2); end;

function f2(x,y1,y2:extended):extended;

begin f2:=-y2/x; end;

function f11(x,y1,y2:extended):extended;

begin f11:=(1/x-sqr(x)*sqr(y2))*f1(x,y1,y2)+(-2*sqr(x)*y1*y2)*f2(x,y1,y2); end;

function f21(x,y1,y2:extended):extended;

begin f21:=-1/x*f2(x,y1,y2); end;

begin

k := 0; eps1:={-}1e-5{-6}{-7}{-8}{-17}{-7}{-10};eps2:={-}1e-5{-6}{-7}{-8}{-17}{-7}{-10};

y1:= eps1; y2 := eps2; x:=1; while x <=xn do begin

y1 := y1 + h * f1(x,y1,y2); y2 := y2 + h * f2(x,y1,y2); k:=k+1; if k = tt then

begin z1:=y1/eps1; z2:=y2/eps2; writeln(‘x=’,x:4,’ ‘,’norma=’,sqrt(sqr(z1)+sqr(z2)):4);

writeln (‘y1=’,y1:4,’ ‘,’f1=’,f1(x,y1,y2):4,’ ‘,’f11=’,f11(x,y1,y2):4);

writeln (‘y2=’,y2:4,’ ‘,’f2=’,f2(x,y1,y2):4,’ ‘,’f21=’,f21(x,y1,y2):4); writeln; k:=0

end; x:=x+h; end; readln

end.

Результат работы программы:

x= 1.1E+0001 norma= 1.1E+0001

y1= 1.1E-0004 f1= 1.0E-0005 f11= 9.1E-0007

y2= 9.1E-0007 f2=-8.3E-0008 f21= 7.5E-0009

x= 2.1E+0001 norma= 2.1E+0001

y1= 2.1E-0004 f1= 1.0E-0005 f11= 4.8E-0007

y2= 4.8E-0007 f2=-2.3E-0008 f21= 1.0E-0009

………………………………………………..

x= 2.2E+0003 norma= 2.2E+0003

y1= 2.2E-0002 f1= 1.0E-0005 f11= 4.6E-0009

y2= 4.6E-0009 f2=-2.2E-0012 f21= 1.0E-0015

x= 2.2E+0003 norma= 2.2E+0003

y1= 2.2E-0002 f1= 1.0E-0005 f11= 4.6E-0009

y2= 4.6E-0009 f2=-2.1E-0012 f21= 9.9E-0016

………………………………………………..

x= 8.1E+0003 norma= 8.1E+0003

y1= 8.1E-0002 f1= 1.0E-0005 f11= 1.2E-0009

y2= 1.2E-0009 f2=-1.5E-0013 f21= 1.9E-0017

x= 8.1E+0003 norma= 8.1E+0003

y1= 8.1E-0002 f1= 1.0E-0005 f11= 1.2E-0009

y2= 1.2E-0009 f2=-1.5E-0013 f21= 1.9E-0017

………………………………………………..

x= 1.0E+0004 norma= 1.0E+0004

y1= 1.0E-0001 f1= 1.0E-0005 f11= 1.0E-0009

y2= 1.0E-0009 f2=-1.0E-0013 f21= 1.0E-0017

x= 1.0E+0004 norma= 1.0E+0004

y1= 1.0E-0001 f1= 1.0E-0005 f11= 1.0E-0009

y2= 1.0E-0009 f2=-1.0E-0013 f21= 1.0E-0017

В строке со значениями y1, f1, f11, т.е. со значениями y1, f1, 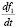, первый компонент решения, его первая и вторая производная имеют совпадающие знаки +, +, +. Согласно теореме 6 это указывает на неустойчивость нулевого решения задачи (30). На то же согласно следствию 3 указывает монотонный рост нормы, нарушающий неравенство (16). С точностью до значений коэффициентов этот результат сохраняется при всех закомментированных возмущениях нулевого начального вектора. Относительно применимости данных критериев к неавтономной системе (30) дословно повторяется замечание 3.

В заключение можно отметить, что предложенные методы численного моделирования устойчивости сохраняют отличие от известных методов по своему построению, инвариантности относительно класса задач и по результатам компьютерного анализа устойчивости. В частности отличия относятся к методам, основанным на традиционных подходах [3, 4], к методам, использующим компьютерные технологии [15, 16], к аналитическим методам [17, 18].

Заключение

С помощью численного эксперимента показано, что для компьютерного анализа устойчивости в смысле Ляпунова, выполняемого на основе предложенных критериев, применимы различные разностные методы приближенного решения задачи Коши для системы ОДУ. Наиболее быстро решает задачу компьютерного анализа устойчивости метод Эйлера, накопление погрешности этого метода, как правило, не влечет ошибки в оценке устойчивости на отрезках приближения сравнительно небольшой длины. Разностные методы Рунге – Кутты, Батчера, Дормана – Принса более точны и аналогично применимы для анализа устойчивости. Вместе с тем по быстродействию они уступают кусочно-интерполяционному методу с итерационным уточнением на основе интерполяционного полинома Лагранжа. Этот метод вследствие меньшего накопления погрешности сравнительно адекватно выражает асимптотическое поведение и определяет устойчивость решения задачи Коши для системы ОДУ. Применение метода позволяет в целом эффективно и достоверно выполнять компьютерный анализ устойчивости на основе численного моделирования в рамках предложенных критериев, в частности он может применяться для анализа устойчивости в реальном времени по ходу решения задачи.

Библиографическая ссылка