Актуальность статьи обусловлена необходимостью постепенного улучшения содержания обучения студентов различным дисциплинам из областей информатики и математики, выявления в нем недостатков. Это будет повышать весьма невысокую степень дружественности этих дисциплин для студентов.
Цель настоящего исследования – инициировать указанное выше постепенное улучшение содержания обучения и выявление в нем недостатков.
Материалы и методы исследования
Материалы исследования в данном случае – это учебные материалы по информатике и математике в современной высшей школе, включая также опыт преподавания автора статьи. В данной статье применяются главным образом эвристические методы исследования для улучшения содержания обучения студентов и выявления укоренившихся недостатков.
Результаты исследования и их обсуждение
1. О понятии алгоритма в информатике и в математике
Понятие алгоритма из информатики имеет источником [1] работы IX в. Мухаммада ибн Муса аль-Хорезми «Книга об индийской арифметике» и «Книга о восстановлении и противопоставлении». Под алгоритмом понимался способ решения математической задачи, например умножение 345,19 на 20,123 в столбик, решение алгебраических уравнений и неравенств. Построение по Г. Кантору бесконечной последовательности M0, M1, M2, ... все более мощных множеств |Mi + 1|>|Mi|, где Mi + 1 = 2Mi – это, по аль-Хорезми, тоже алгоритм. Если, например, M0 – счетное множество, то |M1| = Continuum, |M2| > Continuum и так далее. При этом мы решаем задачи построения каждого элемента этих множеств. Мощность множества всех алгоритмов по аль-Хорезми превосходит Continuum. Алгоритм из математики – это одна из программ для одной из машин Тьюринга. Машина Тьюринга для некоторых m,n∈N, N – множество всех натуральных чисел – это дискретная (разбитая на клетки) бесконечная в обе стороны лента. Лента имеет указатель, который показывает в каждый дискретный момент времени t0, t1, t2, ... на некоторую клетку – это выделенная клетка. Имеется множество состояний машины S = {s0, s1, ..., sn}, s0 – конечное состояние. Имеется алфавит для ленты A = {a0, a1, ..., am}, a0 – это пробел. В каждой клетке записан некоторый символ из A, он может быть заменен другим по команде. Команда Kij (где i = 0,...,n, j = 0,...,m) записывается как упорядоченная тройка (sp, aq, P), где P∈{L,R,S}. Означает она, соответственно: изменение состояния машины si→sp (если оно было si); замена символа в выделенной клетке aj→aq (если он был aj); P – изменение положения указателя: L – сдвиг влево (Left), R – сдвиг вправо (Right), S – положение не меняется (Stop). Машина будет выполнять команды, пока ее состояние не станет конечным. Следовательно, количество всевозможных команд x = 3n(m + 1). Программа – это прямоугольная матрица команд Kij для i = 1,...,n, j = 0,...,m, в ней y = n(m + 1) элементов. При фиксированных m, n получается не более z = xy различных программ, z (m, n) – это конечное число. Как известно, N2 – счетное множество, следовательно, оно может быть представлено как последовательность b1, b2, ..., где всякое bi – это некоторая пара (m,n). На шаге 1 пронумеруем z(b1) программ, на шаге 2 пронумеруем z(b2) программ и так далее. Множество всех алгоритмов из математики – счетное. Aлгоритмы из информатики и из математики – это не тождественные понятия. Кардинально что-либо исправить здесь невозможно, это складывалось десятилетиями, но следует хотя бы обратить на это внимание студентов.
2. О вычислениях в программировании и математике
Стандарт IEEE-754 представляет двоичные форматы целых и действительных чисел для любых современных компьютеров. Пусть, например, программирование ведется на C + + в среде Microsoft Visual Studio – согласно программе Microsoft Dreams Park [2] этот программный продукт является бесплатным для сферы образования, поэтому широко распространен в сфере образования России. Оператор int i = 3; /* целому i присвоить 3 – в С + + так пишутся комментарии */ вызовет запись в 32-битное поле i следующего двоичного кода 0000 0000 0000 0000 0000 0000 0000 0011, а оператор int j = -3; вызовет следующие действия: сначала в поле j запишется число 3, значит – указанный выше код, потом код будет инвертирован, получится 1111 1111 1111 1111 1111 1111 1111 1100, затем к нему прибавится 1, окончательно получится 1111 1111 1111 1111 1111 1111 1111 1101. Отсюда диапазон значений переменных типа int от –2(32-1) до 2(32-1)-1, если бы длина поля была N бит (в данном случае N = 32), то соответствующий диапазон был бы от –2(N-1) до 2(N-1)-1. Оператор unsigned int k = 3; /* беззнаковому целому k присвоить 3 */ вызовет запись в 32-битное поле k двоичного кода 0000 0000 0000 0000 0000 0000 0000 0011, как выше для i, но диапазон значений для k будет иной – от 0 до 2N-1, здесь N = 32. Например, для типов данных long int и unsigned long int (длинное целое и беззнаковое длинное целое) битовая длина поля N = 64. Зачем нужны в программировании целые числа, например, типа int? Функционально они уступают действительным числам, например, типа double. Программисты называют целые числа точными [3], поскольку результаты арифметических действий над ними всегда абсолютно точны. Действительные числа они называют приближенными. Финансовые программы используют только целые числа. Если у чисел типа int разрядов слишком мало для выполнения расчетов, то используют типы long int, long long int. Циклические расчеты надежнее, когда счетчики (управляющие циклом переменные) являются целыми, другие вычисляемые при этом переменные могут быть действительными.
Формат действительного числа
|
1 бит – поле S |
b битов – поле E |
n битов – поле M |
|
w = n + b + 1 |
||
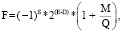 (1)
(1)
где 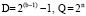
Представление действительного числа F типов float (b = 8, n = 23, w = 32) и double (b = 11, n = 52, w = 64) описывают табл. 1 и формула (1).
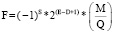 (2)
(2)
Формула (1) не применима:
1) если E = 0, M ≠ 0, тогда F – действительное с денормализованной мантиссой, формула (2);
2) если E = 1...1, M ≠ 0, тогда F = NAN (Not A Number, не число);
3)если S = 0, E = 1...1, M = 0, тогда F = + ∞, если S = 1, E = 1...1, M = 0, тогда F = -∞;
4)если S = 0, E = 0, M = 0, тогда F = + 0, если S = 1, E = 0, M = 0, тогда F = -0.
Из формулы (1) следует, что положительный диапазон типа double – от 2.2e-308 до 1.8e308, типа float – от 1.2e-38 до 3.4e38. Если требуются типы данных с более широкими диапазонами, то их можно построить, например, как новые классы, используя объектно-ориентированное программирование. Поскольку 100!>1.8e308, после оператора double f; применяя только программирование со стандартными типами данных, не удастся вычислить 100! с результатом в f, несмотря на то, какой применяется алгоритм расчета.
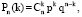 (3)
(3)
где 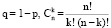
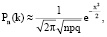 (4)
(4)
где 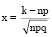 .
.
Из теории вероятностей известна формула Бернулли (3), где Pn(k) – это вероятность ровно k успехов в n испытаниях, p – вероятность успеха в одном испытании. В практике программирования со стандартными типами данных при n ≥ 100 формулу (3) применять нельзя – можно вместо точной формулы Бернулли использовать, например, приближенную локальную формулу Лапласа (4).
3. О визуальном программировании
Упоминавшаяся выше Microsoft Visual Studio – это мультиязыковая система визуального программирования, в ее составе Visual Basic, Visual C + + , Visual C#, Visual F#, Visual FoxPro. Она ориентирована на визуальное программирование [2], но в виде исключения допускает программирование 1960–1970-х гг. в режимах консольного приложения и пустого проекта. Ни в одном вузе автору не доводилось видеть преподавание визуального программирования, кроме, естественно, преподавания визуального программирования самим автором, которое началось еще в 1990-х гг. В 2010–2013 гг. выпускались учебные пособия В.В. Зиборова [4, 5], посвященные визуальному программированию на Visual Basic, Visual C + + , Visual C#, где читатель при создании своих проектов должен был главным образом рисовать объекты управления и в меньшей степени – изучать операторы языков программирования. В результате читатель добирался в рамках такой методики обучения до очень сложных программ, например до работы программ с динамическими библиотеками, с сетевыми ресурсами, с базами данных. Автор настоящей статьи указывал [6], что более 80 % современных студентов – правополушарные, даже среди будущих математиков и программистов. Им при обучении необходима наглядность.
4. Обсуждение определения понятия определенного интеграла
В учебных пособиях по [7] математическому анализу и по [8] высшей математике применяются два подхода к определению понятия определенного интеграла. Сущность первого подхода такова:
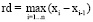 , (5)
, (5)
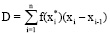 , (6)
, (6)
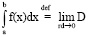 . (7)
. (7)
Рассмотрим функцию f(x), заданную для x∈[a;b]. Разобьем [a;b] на n не обязательно равных по длине отрезков точками a = x0<x1<x2<...<xn = b. Пусть ранг дробления rd определяется формулой (5). Возьмем xi*∈(xi-1;xi) для i = 1...n. Пусть сумма Дарбу D определяется формулой (6). Пусть предел из формулы (6) не зависит от конкретных значений xi и xi*. Тогда формула (7) определяет определенный интеграл от функции f на [a;b], а функция f∈L[a;b] – классу функций, интегрируемых на [a;b]. Заметим, что различным значениям rd может соответствовать одинаковое значение D, поэтому D не является функцией от rd, D зависит от x1, ..., xn-1 и от x1*, ..., xn*, говорить о пределе из формулы (7) не совсем корректно. Сущность второго подхода такова:
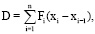 (8)
(8)
где 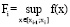
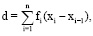 (9)
(9)
где 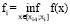
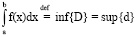 . (10)
. (10)
Нужно рассмотреть ограниченную функцию f: m<f(x) < M при всех x∈[a;b]. Нужно ввести верхнюю D и нижнюю d суммы Дарбу в соответствии с формулами (8) и (9). Если окажется так, что inf всевозможных значений D равен sup всевозможных значений d, то формула (10) определяет определенный интеграл от функции f на [a;b], а функция f∈L[a;b]. Из [7] аксиомы действительных чисел о sup (всякое ограниченное сверху числовое множество имеет sup) несложными рассуждениями можно получить, что все указанные выше inf и sup существуют.
5. Прямая на плоскости R2 в аналитической геометрии
Согласно учебным пособиям [8–10], используемым при обучении аналитической геометрии Ax + By + C = 0 – это общее уравнение прямой на плоскости R2, при условии, что A2 + B2>0, здесь R – множество всех действительных чисел. В некоторых [9, 10] учебных пособиях – это теорема. При этом в них нет определения прямой. По нашему мнению, некорректно доказывать теорему про прямую, если не известно, что такое прямая. Мы предлагаем семейство уравнений Ax + By + C = 0 при условии, что A2 + B2 > 0 положить в основу определения прямой линии на плоскости R2. Прямая – это множество точек (x, y), удовлетворяющих одному из уравнений семейства. Аналогично мы предлагаем положить в основу определения плоскости в пространстве R3 семейство уравнений Ax + By + Cz + D = 0 при условии, что A2 + B2 + C2 > 0. Некоторые авторы [8] дают определения, что такое общие уравнения прямой в R2 и плоскости в R3, при этом определения прямой у них нет.
Геометрия средней школы ориентируется на геометрию Евклида с аксиомами Евклида – это другая математическая теория. Все аксиомы Евклида в совокупности неявно определяют понятие прямой вместе с другими так называемыми основными неопределяемыми понятиями (точка, полупрямая, полуплоскость, угол и другие). Явных определений у этих понятий в геометрии Евклида нет, но теоремы про них могут выводиться из аксиом Евклида. В высшей школе изучают аналитическую геометрию Декарта, в ней есть только аксиомы действительных чисел. Некорректно, работая в рамках одной математической теории, применять аксиомы из другой математической теории.
6. О вопросах, связанных с возведением в степень комплексного числа
Здесь и далее будем использовать обозначения: С – множество всех комплексных чисел, i = (0;1)∈C, e – число Эйлера и Непера, ln – натуральный логарифм (по основанию e).
eiw = cos w + i sin w (11)
для любого w∈R.
Формула Эйлера (11) обычно изучается в курсах алгебры в теме «Комплексные числа». По нашему мнению, ее следует считать определением того, что понимать под eiw, поскольку ранее в таких учебных курсах ничего не говорится про то, что это такое, поэтому доказывать формулу Эйлера как теорему некорректно. С помощью (11) мы для любых d > 0 и z ∈ C можем вычислить dz. Пусть z = a + ib, очевидно, что d = eln d, тогда
dz = (eln d)a + ib = ea ln d eib ln d =
= ea ln d (cos(b ln d) + i sin(b ln d)) ∈ C.
Введем ln z, как операцию, обратную к ex, где z,x∈C, z ≠ 0 и z ≠ ∞. Представим z в следующем виде:
z = |z|(cos w + i sin w) = |z| eiw,
берем главное значение w: -π<w≤π. Определим ln z = ln|z| + iw, берем то же главное значение w, хотя тоже подходят w + 2πk, k∈Z, Z – множество целых чисел.
Теперь мы для любых z,x∈C при z ≠ 0 и z ≠ ∞ научимся вычислять zx = (eln z)x = ex ln z, x ln z ∈С – умеем вычислять, следовательно, zx = ex ln z – тоже умеем вычислять.
7. Некоторые вопросы проверки статистических гипотез
Пусть выборка x1, x2, ..., xn – это результаты независимых наблюдений (независимые одинаково распределенные случайные величины). Пусть гипотеза H состоит в том, что одинаковое распределение этих случайных величин является нормальным. Здравый смысл заставляет гипотезу H отвергнуть. Нормальные распределения – это весьма специфический класс распределений. Практически невозможно, чтобы некоторое эмпирическое распределение было точно именно таким. Здравый смысл разрешает говорить лишь о близости некоторого эмпирического распределения к нормальному. Актуально было бы эту близость оценить. Классическая центральная предельная теорема говорит лишь о стремлении по вероятности, что на практике никакого конкретного значения близости гарантировать не может. Для этого, например, можно было бы каким-либо образом ввести и использовать метрику в пространстве функций распределения.
Рассмотрим теоретически алгоритм проверки некоторой гипотезы H. Отвержение верной гипотезы называют ошибкой 1 рода. Принятие неверной гипотезы называют ошибкой 2 рода. Уровень значимости – это мажоранта вероятности ошибки 1 рода. Можно было бы ввести и уровень значимости 2 рода как мажоранту вероятности ошибки 2 рода, но, как правило, вычислить его невозможно. Для проверки гипотезы H имеется выборка x1, x2, ..., xn – такая же, как указано выше. Вычисляется значение некоторой статистики t* = T(x1, x2, ..., xn). Вероятностное распределение T известно при условии, что верна гипотеза H. Пусть распределению T соответствует функция распределения F(t), она обычно табулирована. Полагают, например, что уровень значимости λ = 0.05. На оси t берут критическую область K так, чтобы P{t*∈K} = λ, допустимой областью называют D = R\K. Если вычисленное значение t*∈D, то гипотеза H принимается, в противном случае (t*∈K) гипотеза H отвергается. Обычно критическую область берут состоящей либо из одного промежутка (K = <a1;b1>), либо из двух промежутков (K = <a1;b1> ∪ <a2;b2>) – это все определяется особенностями гипотезы H. Соответственно, должно быть либо F(b1)-F(a1) = λ, либо F(b1)-F(a1) + F(b2)-F(a2) = λ.
Допустим, гипотеза H таким образом была отвергнута. Какая могла быть ошибка в данном случае? Это ошибка отвергнуть верную гипотезу H, т.е. ошибка 1 рода. Мажоранта ее вероятности известна (λ = 0.05). Отвергнув гипотезу H, мы могли ошибиться, но вероятность ошибки при этом не более, чем 0.05.
Допустим, гипотеза H таким образом была принята. Какая могла быть ошибка в данном случае? Это ошибка принять неверную гипотезу H, т.е. ошибка 2 рода. Ее вероятность – это P{t*∈D} при условии, что гипотеза H неверна, но обычно при этом условии распределение статистики T неизвестно! Никак оценить вероятность актуальной для нас ошибки 2 рода мы не можем.
У автора статьи имеется [11] многократно использованная практически собственная методика статистической обработки результатов педагогических экспериментов, лишенная отмеченных выше недостатков. Ее можно распространить на эксперименты в других областях. Эксперимент планировался так, чтобы гипотеза H всегда отвергалась.
Заключение
1. Цель настоящего исследования достигнута – предложены улучшения и выявлены некоторые недостатки в семи содержательных областях при обучении математике и информатике.
2. Применение материалов статьи может повысить для студентов дружественность обучения математике и информатике, повысить интерес к ним.
Библиографическая ссылка
Фокин Р.Р. О СОДЕРЖАТЕЛЬНОМ АСПЕКТЕ ОБУЧЕНИЯ МАТЕМАТИКЕ И ИНФОРМАТИКЕ В СОВРЕМЕННОЙ ВЫСШЕЙ ШКОЛЕ // Современные наукоемкие технологии. 2021. № 6-2. С. 340-344;URL: https://top-technologies.ru/ru/article/view?id=38745 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.38745



