Учитывая тот факт, что электронная коммерция, банковское дело и бизнес связаны с конфиденциальной и ценной информацией, передаваемой по сети, нет необходимости упоминать о важности анализа сетевого трафика для достижения надлежащей информационной безопасности. Анализ сетевого трафика является важным этапом для разработки успешных систем предупредительного контроля перегрузок и выявления нормальных и вредоносных пакетов в сети [1]. Для анализа сетевого трафика можно математически смоделировать его поведение с помощью временного ряда, в котором значения ряда будет представлять собой набор параметров, характеризующих работу сети, таких как ip/port/mac адреса source и destination и др. Анализ этих временных рядов предоставит информацию о таких характеристиках трафика, как тренд, сезонность и др. для ежедневного набора данных. В свою очередь, это позволяет выделять трафик, нестандартный для данного сегмента сети и который требует повышенного внимания и дополнительного анализа.
Материал и методы исследования
1. Прогнозирование временных рядов (Time series forecasting)
Прогнозирование временных рядов является сложной задачей. Это сложно даже для нейронных сетей с присущей им способностью к обучению. В данной статье представлена система прогнозирования временных рядов на основе нейронных сетей, охватывающая разработку признаков, их важность, точечное и интервальное прогнозирование и оценку прогнозов. Описание метода сопровождается исследованием, с использованием сетей LSTM и GRU.
Временной ряд – это хронологически упорядоченные наблюдения xt, записанные в определенное время t. Если набор временных шагов равен T, где t ∈ T дискретно, то такой временной ряд называется дискретным, а если наблюдения записываются непрерывно в течение некоторого интервала времени, то временной ряд является непрерывным [2]. Целью анализа временных рядов обычно является построение модели и подгонка ее к наблюдениям для изучения зависимостей в наборе данных. Цель состоит в том, чтобы понять механизм возникновения наблюдений, найти закономерности и предсказать дальнейшее развитие наблюдаемых переменных. Временные ряды можно разделить на несколько компонентов, которые представляют основной тип закономерности: тренд, сезонность, циклы и остаточный компонент.
- Tt : тренд – возрастающее или убывающее значение,
- St : сезонность – повторяющийся краткосрочный цикл с известной частотой,
- Ct : циклы также повторяются, частота не точная,
- Rt : оставшаяся часть захватывает все остальное.
Если мы предполагаем аддитивное разложение, то путем сложения этих компонентов получается исходный временной ряд
yt = Tt + St + Ct + Rt .
Если вариации вокруг тренда или величина сезонных колебаний не отличаются от уровня (ожидаемого значения) временного ряда, подходит аддитивное разложение. В противном случае больше подходит мультипликативная декомпозиция
yt = Tt × St × Ct × Rt .
2. Нейронные сети для прогнозирования
Цель обучения с использованием нейронных сетей состоит в том, чтобы дать предсказание на основе данных. Обучающий набор выходных (целевых) данных и некоторых входных переменных подается в алгоритм, который учится предсказывать целевые значения. Выходные данные могут быть категориальными (классификация) или непрерывными (регрессия). Задача алгоритма состоит в том, чтобы обеспечить высокое качество прогнозов, извлекая необходимые знания исключительно из имеющихся данных.
Нейронные сети – популярная структура для контролируемого обучения, это сетевая система взвешенных сумм и дифференцируемых функций, которая может изучать сложно организованные структуры. Обычно для нахождения оптимальных значений весов сети используются варианты градиентного спуска вместе с обратным распространением (правило цепочки). Построение сети просто и интуитивно понятно, но результаты трудны для понимания. Существует много весов и связей, и не всегда объясняется, как система дала тот или иной результаты. Причина высокой популярности нейронных сетей проста: они хороши в изучении произвольно сложных функций и часто дают отличные прогнозы для довольно сложных задач машинного обучения.
2.1 Рекуррентные нейронные сети
Рекуррентные нейронные сети (RNN) представляют собой модели искусственной нейронной сети (ANN), предложенные в 1980-х годах (Rumelhart et al., 1986; Эльман, 1990; Werbos, 1988), которые позволяют оперировать последовательностями векторов. Они применяются при создании рукописного текста, машинном переводе, распознавании речи, классификации видео, субтитрах и других задачах. Ключевое различие между нейронными сетями прямого распространения (FNN) и RNN заключается в том, что RNN имеют память, в которой они хранят информацию, вычисленную на основе предыдущих входов, то есть на последний выход влияет не только предыдущий вход, но и все входы, которые были поданы в сеть. На рисунке 1 показано несколько примеров того, как может быть спроектирована структура сети в зависимости от того, является ли вход или выход (или и то, и другое) последовательностью [3]. Красные прямоугольники представляют входные векторы, синие прямоугольники – выходные векторы, а зеленые прямоугольники – (скрытые) блоки RNN. Существует поток данных не только из входного слоя через скрытый слой в выходной слой, но зеленые стрелки представляют поток между блоком RNN и его преемником. На рисунке 2 нет потока между нейронами в одном слое, в отличие от рисунка 3. Подача входных данных в FNN и RNN отличается. Если рассматривать предложение как входные данные в FNN, то в RNN предложение будет разбито на слова (или символы, в зависимости от задачи), и будет подаваться одно слово за раз.
Есть две популярные и эффективные модели РНС, которые действительно хорошо работают: долгосрочная краткосрочная память и рекуррентный блок с управляемой памятью.

Рис. 1. Варианты структуры рекуррентных нейронных сетей
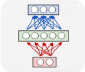
Рис. 2. Структура сети прямого распространения
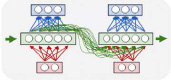
Рис. 3. Развернутая структура сети прямого распространения в течение 2 временных шагов
2.1.1 Сети долгосрочной краткосрочной памяти, Long Short-Term Memory (LSTM)
Сети долгосрочной краткосрочной памяти (впервые представленные в 1997 году Хохрайтером и Шмидхубером) имитируют способ обработки последовательных данных человеческим мозгом. Хорошим примером является чтение текста – чтобы запомнить достоверную информацию, мы забываем повторяющиеся части текста [4]. Хотя у RNN есть проблемы с долгосрочными зависимостями, модули LSTM решают эту проблему с помощью дополнительных функций.
Такие сети имеют 3 шлюза, которые управляют содержимым памяти. Эти шлюзы являются простыми логистическими функциями взвешенных сумм, где веса могут быть усвоены при обратном распространении. Это означает, что, хотя это кажется немного сложным, LSTM идеально вписывается в нейронную сеть и ее тренировочный процесс. Она может узнать, чему она должна научиться, запомнить то, что ей нужно запомнить, и вспомнить то, что ей нужно вспомнить, без какого-либо специального обучения или оптимизации. Входной шлюз (1) и забытый шлюз (2) управляют состоянием ячейки (4), которое является долговременной памятью. Выходной шлюз (3) создает выходной вектор или скрытое состояние (5), которое является памятью, сфокусированной для использования. Эта система памяти позволяет сети запоминать на долгое время, чего сильно не хватало в обычных рекуррентных нейронных сетях.
it = sigmoid (Wixt + Uiht–1 + bi ) (1)
ft = sigmoid (Wf xt + Uf ht–1 + bf ) (2)
ot = sigmoid (Woxt + Uoht–1 + bo ) (3)
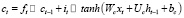 (4)
(4)
 (5)
(5)
2.1.2 Cети с рекуррентным блоком управляемой памяти, Gated Recurrent Unit (GRU)
Несмотря на то что в сообществе машинного обучения часто используется название LSTM Autoencoder, Seq2Seq модели применяются не только к блокам LSTM. Существуют и другие варианты блоков LSTM. На сегодняшний день наиболее популярным является Gated Receivative Unit (GRU). Блок создается блоком LSTM, объединяющим забытый и входной вентиль в вентиль обновления zt. Этот модуль управляет тем, сколько информации из предыдущего скрытого состояния передается в следующее скрытое состояние, позволяя фиксировать долгосрочные зависимости без необходимости иметь состояние ячейки. Это означает, что модуль проще в вычислении, потому что есть меньше параметров.
Поскольку он не имеет выходного вентиля, отсутствует управление содержимым памяти. Затвор (6) обновления управляет потоком информации от предыдущей активации, а также добавлением новой информации (8), в то время как затвор (7) сброса вставляется в активацию кандидата. В целом он довольно похож на LSTM. Только из этих различий трудно сказать, какой из них является лучшим выбором для данной проблемы/
zt = sigmoid (Wzxt + Uzht–1 + bz ) (6)
rt = sigmoid (Wrxt + Urht–1 + br ) (7)
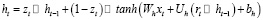 (8)
(8)
3. Характеристики
3.1 Разработка функций
Сети LSTM и GRU могут обучаться и запоминать характеристики временных рядов. Однако это не так просто, особенно когда у нас есть только короткая серия значений для обучения. Здесь может помочь умная инженерия характеристик. Существует очень мало вещей, будущие значения которых мы точно знаем [5; 6]. Время является одной из таких вещей – мы всегда знаем, как оно проходит. Поэтому мы можем использовать его для составления прогнозов, даже на несколько шагов вперед в будущее, без увеличения неопределенности. Все, что нам нужно сделать – это извлечь полезные характеристики, которые наш алгоритм сможет легко интерпретировать.
Компоненты временного ряда, такие как тренд или сезонность, могут быть закодированы во входных переменных, как и любое детерминированное событие или условие. Сдвинутые во времени значения целевой переменной также могут быть полезными предикторами. Характеристики обычно нормализуются перед подачей в нейронную сеть. Это полезно для процесса обучения. Двумя популярными вариантами изменения масштаба переменных являются минимаксный (9) и стандартный (10):
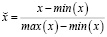 (9)
(9)
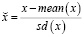 (10)
(10)
3.2 Задержки
Задержка означает возвращение на несколько шагов назад во времени. Чтобы предсказать будущее, прошлое является нашим лучшим ресурсом – неудивительно, что предыдущие значения целевой переменной довольно часто используются в качестве исходных данных для прогнозирования. Можно использовать лаги на любое количество временных шагов. Единственным недостатком использования запаздывающих переменных является то, что мы теряем первые наблюдения – те, чьи сдвинутые значения неизвестны. Это может быть актуально, когда временной ряд короткий.
3.3 Сезонность
Мы можем попытаться найти повторяющиеся закономерности во временном ряду, закодировав сезонные колебания. Существуют различные способы сделать это. Разумным выбором является кодирование по принципу «один к одному». Здесь мы рассматриваем сезонность как категориальную переменную и используем фиктивные переменные для обозначения текущего временного интервала в сезонном цикле. Это просто и интуитивно понятно. Однако он не может действительно уловить цикличность, поскольку расстояние между интервалами не имеет значения во время кодирования. Кроме того, одноточечное кодирование использует отдельную переменную для представления каждого уникального значения, что может быть неудобно при большом количестве временных интервалов. Эти недостатки подхода с фиктивными переменными приводят нас к другому методу кодирования. Мы можем разместить значения на одной непрерывной шкале вместо использования нескольких двоичных переменных. Присваивая возрастающие равноудаленные значения последовательным временным интервалам, мы можем уловить сходство соседних пар, но при таком кодировании первый и последний интервалы оказываются наиболее удаленными друг от друга, что является ошибкой. Это можно исправить, преобразовав значения с помощью преобразования синуса (11) или косинуса (12). Для того чтобы каждый интервал был представлен однозначно, мы должны использовать оба варианта.
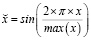 (11)
(11)
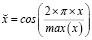 (12)
(12)
3.4 Индикаторы
Мы можем использовать простые индикаторные переменные для событий или условий, которые мы считаем важными. Праздники всегда особенные и проводятся необычным образом. Следовательно, двоичная переменная, указывающая на праздники, может нести информацию о временном ряде. Также может быть полезен индикатор рабочих дней или рабочих часов.
Заключение
В данной работе было проведено исследование и описание вариантов использования нейронных сетей с временными рядами данных, и описаны некоторые аспекты применения нейронных сетей для анализа и прогнозирования сетевого трафика, представленного в виде временных рядов, хотя они далеко не всеобъемлющие. Рекуррентные нейронные сети гораздо более гибкие и гораздо лучше подходят для прогнозирования временных рядов, чем обычно применяемые линейные модели. Тем не менее с помощью методов, описанных в этой статье, можно решить данные проблемы. Мы можем проводить анализ временных рядов с целью либо прогнозирования будущих значений, либо понимания процессов, движущих временными рядами, но нейронные сети особенно плохи в последнем случае. Важно понимать, что использование нейронных сетей необходимо для расширения функционала традиционных методов в области обнаружения вторжения в сеть передачи данных, а не для полного их замещения.
Библиографическая ссылка
Казаков Ф.А., Шнайдер А.В. ИСПОЛЬЗОВАНИЕ НЕЙРОННЫХ СЕТЕЙ С ВРЕМЕННЫМИ РЯДАМИ ДАННЫХ ДЛЯ АНАЛИЗА ПОТОКОВ ДАННЫХ // Современные наукоемкие технологии. 2021. № 6-2. С. 260-264;URL: https://top-technologies.ru/ru/article/view?id=38731 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.38731



