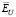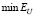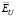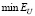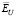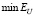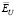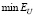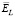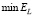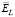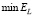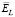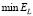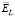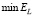Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Воскобойников Ю.Е. 1, 2 Боева В.А. 1

---

1 ФГБОУ ВО «Новосибирский государственный архитектурно-строительный университет (Сибстрин)»

2 ФГБОУ ВО «Новосибирский государственный технический университет»

Сглаживающий кубический сплайн дефекта единица является достаточно универсальным инструментом для фильтрации шумов измерения, как в одномерных, так и в двумерных сигналах. В силу непрерывности своей первой и второй производной на всем интервале определения сплайна, он применяется для построения эффективных алгоритмов непараметрической идентификации, в которых используются первые производные как входного, так и выходного сигналов идентифицируемой системы. Ошибка сглаживания (как и ошибка дифференцирования) существенно зависит от величины так называемого параметра сглаживания. При малых значениях этого параметра фильтрация шумов незначительна, и вычисленная первая производная имеет осциллирующую форму, что характерно для неустойчивых решений некорректно поставленных задач. При больших значениях параметра график сплайна стремится к прямой линии (вторая производная стремится к нулю), и происходит существенное «сглаживание» информативных составляющих обрабатываемой функциональной зависимости. Между этими двумя предельными значениями находится значение параметра (назовем его оптимальным), для которого ошибка сглаживания минимальна. К сожалению, точное значение оптимального параметра на практике вычислить не удается (из-за отсутствия априорной информации о характеристиках «точного» сигнала). Поэтому на практике используются различные алгоритмы выбора этого параметра, дающие приемлемые ошибки сглаживания, но превышающие (иногда значительно) минимальное значение. Следует выделить два случая: когда дисперсия шума измерения достоверно известна и когда такая информация отсутствует. Если в первом случае алгоритмы выбора позволяют достаточно точно оценить оптимальное значение параметра сглаживания, то в случае неизвестной дисперсии вопрос такого оценивания остается открытым, особенно в случае коррелированного шума измерения. Поэтому в данной работе подробно исследуются два алгоритма выбора параметра сглаживания при неизвестной дисперсии шума измерения. Особое внимание при этом уделяется оцениванию оптимального параметра в условиях коррелированного шума. По результатам этих исследований даются практические рекомендации по построению сглаживающих сплайнов в задачах непараметрической идентификации.

Статья в формате PDF

0 KB

фильтрация шумов

сглаживающие кубические сплайны

параметр сглаживания

выбор параметра при неизвестных дисперсиях шума

1. Сидоров Д.Н. Методы анализа интегральных динамических моделей: теория и приложения. Иркутск: Изд-во ИГУ, 2013. 293 с.

2. Бахтадзе Н.Н., Гинсберг К.С., Боровских Л.П. Идентификация систем на пути создания общей теории идентификации объектов управления // Проблемы управления. 2015. № 3. С. 79–83.

3. Воскобойников Ю.Е. Устойчивые алгоритмы непараметрической идентификации динамических систем. Новосибирск: Изд-во НГАСУ (Сибстрин), 2019. 156 с.

4. Солодуша С.В. К численному решению одного класса систем полиномиальных уравнений Вольтера I рода // Сибирский журнал вычислительной математики. 2018. № 1. С. 117–126.

5. Воскобойников Ю.Е., Боева В.А. Новый устойчивый алгоритм непараметрической идентификации технических систем // Современные наукоемкие технологии. 2019. № 5. С. 25–29.

6. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. 345 с.

7. Wang Y. Smoothing Splines Methods and Applications. Ser. Monographs on Statistics and Applied Probability v. 121. A Chapman & Hall book. 2011. 347 p.

8. Воскобойников Ю.Е., Преображенский Н.Г., Седельников А.И. Математическая обработка эксперимента в молекулярной газодинамике. Новосибирск: Наука, 1984. 238 с.

9. Kohavi R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. 14th International Joint Conference on Artificial Intelligence, Palais de Congres Montreal, Quebec, Canada. 1995. P. 1137–1145.

10. Долишний В.В., Жданов А.И. Экономичный метод многократного решения расширенных регуляризованных нормальных систем уравнений // Вестник Самарского государственного технического университета. Серия: Физ.-мат. науки. 2012. № 1 (26). С. 214–222.

11. Kerkri A., Allal J., Zarrouk Z. The L-Curve Criterion as a Model Selection Tool in PLS Regression. Journal of Probability and Statistics. 2019. Vol. 8. Article ID 3129769. doi.org/10.1155/2019/3129769

12. Xu Y., Pei1 Y., Dong F. An extended L-curve method for choosing a regularization parameter in electrical resistance tomography. Measurement Science and Technology. 2016. Vol. 27. No. 11. Р. 21–32.

Для описания поведения линейных стационарных динамических систем в терминах «вход-выход» часто используется математическая модель в виде интегрального уравнения Вольтера I рода [1, 2]:

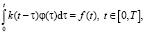(1)

где k(t) – импульсная переходная функция (ИПФ) системы (ядро интегрального уравнения); φ(τ), f(t) – входной и выходной сигналы системы. Для такой математической модели задача непараметрической идентификации заключается в построении оценки для ИПФ k(t) по зарегистрированным в эксперименте значениям входного и выходного сигнала, т.е. необходимо решить уравнение (1) относительно k(t). Как известно, такая задача является некорректно поставленной. Для построения устойчивого (к погрешностям исходных данных) решения возможны два подхода. В первом подходе уравнение (1) аппроксимирует дискретной сверткой, и ее решение находят с помощью регуляризирующего алгоритма, основанного на использовании дискретного преобразования Фурье и алгоритма быстрого преобразования Фурье [3]. Второй подход заключается в сведении уравнения (1) к интегральному уравнению второго рода, решение которого уже является корректно поставленной задачей, но само уравнение включает первые производные входного и выходного сигналов идентифицируемой системы [4, 5]. Дифференцирование зашумленных сигналов также является некорректно поставленной задачей, но этот подход авторам работы представляется более предпочтительным – подробную аргументацию можно увидеть в публикации [5]. Здесь же только заметим, что, используя для фильтрации шумов сглаживающие кубические сплайны (СКС), удается эффективно подавлять шум измерения не только выходного сигнала идентифицируемой системы, но и шум измерения входного сигнала, что весьма затруднительно сделать в первом подходе. Главной проблемой при использовании СКС на практике является выбор параметра сглаживания, от величины которого существенно зависит ошибка сглаживания. Очевидно желание выбрать такое значение (назовем его оптимальным), при котором величина ошибки была бы минимальной. Однако из-за отсутствия априорной информации о «точных» значениях обрабатываемой функции вычисление оптимального параметра невозможно. Поэтому на практике используются различные алгоритмы выбора этого параметра, дающие приемлемые ошибки сглаживания, но превышающие (иногда значительно) минимальное значение. Следует выделить два случая: когда дисперсия шума измерения достоверно известна и когда такая информация отсутствует. Если в первом случае есть алгоритмы выбора, которые позволяют достаточно точно оценить оптимальное значение параметра сглаживания, то в случае неизвестной дисперсии вопрос такого оценивания остается открытым, особенно в случае коррелированного шума измерения, т.е. между соседними значениями шума существует значимая корреляция. Такой шум может появиться после предварительной фильтрации зарегистрированных сигналов идентифицируемой системы (например, после фильтрации аномальных измерений).

Целью данной работы является построение и исследование алгоритмов выбора параметра сглаживания при неизвестной дисперсии шума измерения и коррелированном шуме измерения. При этом решаются две задачи: а) построение и исследование алгоритмов выбора параметра сглаживания при неизвестной дисперсии и некоррелированном шуме измерений и б) построение и исследование алгоритмов выбора параметра сглаживания при коррелированном шуме измерений.

Материалы и методы исследования

Сначала приведем некоторые определения и понятия сглаживающего кубического сплайна (СКС), необходимые для дальнейшего изложения алгоритмов выбора параметра сглаживания СКС [6, 7].

Предположим, что на интервале [T1,T2] заданы n узлов 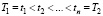, и в этих узлах измерены значения функции:

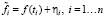, (2)

где ηi – случайный шум измерений с нулевым средним и дисперсией 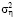(равноточные измерения). Функция Sn(t) называется кубическим сплайном дефекта единица, если:

а) на каждом интервале 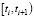функция Sn(t) является кубическим многочленом вида

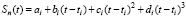(3)

б) функция Sn(t) дважды непрерывно дифференцируема на всем интервале [T1,T2].

В отличие от интерполяционного сплайна, сглаживающий кубический сплайн Sn,α(t) в общем случае не проходит через точки 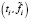, а проходит в некоторой окрестности (ее размеры определяются величиной параметра сглаживания α) от этих точек, обеспечивая тем самым сглаживание (фильтрацию) шума измерений. Для следующих часто используемых на практике краевых условий [6,8]: условия на значения первой производной вида

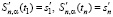, (4)

или условия на нулевые значения второй производной

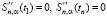. (5)

СКС доставляет минимум функционалу [6,7]:

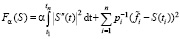, (6)

где pi – весовые множители, отражающие точность i-го измерения 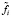(в случае равноточных измерений задаются одинаковыми, например ).

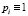Параметр сглаживания α «управляет» гладкостью сплайна, и ошибка сглаживания (как и ошибка дифференцирования) существенно зависит от величины так называемого параметра сглаживания. При малых значениях этого параметра фильтрация шумов незначительна, и вычисленная первая производная имеет осциллирующую форму, что характерно для неустойчивых решений некорректно поставленных задач. При больших значениях параметра график сплайна стремится к прямой линии (вторая производная стремится к нулю), и происходит существенное «сглаживание» информативных составляющих обрабатываемой функциональной зависимости. Между этими двумя предельными значениями находится значение параметра (назовем его оптимальным), для которого ошибка сглаживания (в принятой норме) минимальна. К сожалению, точное значение оптимального параметра на практике вычислить не удается (из-за отсутствия априорной информации о характеристиках «точного» сигнала). Поэтому обратимся к двум методам оценивания параметров алгоритмов регрессионного анализа и регуляризирующих алгоритмов решения некорректных задач и попытаемся их адаптировать для оценивания оптимального параметра сглаживания СКС.

Первоначально рассмотрим метод, который назовем методом перекрестной проверки (или методом перекрестной значимости), в зарубежной литературе – cross-validation method (CVM). Метод использовался при построении моделей (например, [9]) и для выбора параметра регуляризации (например, [10]). Идейная основа этого метода видна из следующих рассуждений [8, с. 68–69].

Предположим, что имеются два вектора 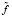и 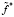размерности n, составленные из двух наборов наблюдений (2). По первому вектору 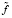построен сплайн Sn,α (t), из значений которого в узлах построен вектор Sn,α. Введем функционал:

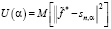, (7)

где математическое ожидание M [·] берется по ансамблю распределения шума измерений ηi, а ||·|| означает евклидову норму вектора. Можно показать, что U(α) допускает представление

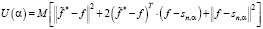, (8)

где f – вектор, составленный из «точных» значений 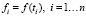. Если математическое ожидание шума измерений равно нулю и шумы измерений двух набора данных не коррелированы между собой, то (8) можно переписать как

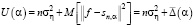, (9)

где второе слагаемое

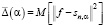(10)

определим как среднеквадратическую ошибку (СКО) сглаживания. Так как первое слагаемое в (9) не зависит от параметра сглаживания α, то минимум U(α) соответствует минимуму СКО, т.е. задача вычисления оптимального параметра αopt, минимизирующего (10), решена. Однако на практике минимизация U(α) сопряжена с двумя трудностями. Во-первых, вычисление математического ожидания в (7) и, во-вторых, отсутствие во многих экспериментах второго набора данных, т.е. вектора 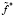. Попытаемся преодолеть эти трудности, перейдя от математического ожидания случайной величины к ее отдельному значению и формируя второй вектор 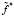из одного набора 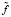данных с помощью следующего алгоритма. Заметим, что предлагаемый способ формирования вектора 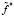отличается от известных [9].

Шаг 1. Все измеренные значения 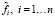, разбиваются на K групп по m измерений в каждой, и в k-ю группу входят измерения: 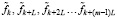, где 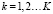, L – периодичность выборки при формировании групп измерений. Задавая величину L, можно определить количество измерений в группе и количество групп:

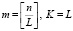, (11)

где 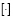– целая часть числа.

Шаг 2. Из экспериментальных значений исключается k-я группа, а по оставшимся n – m значениям строится СКС 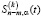и вычисляется величина

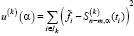, (12)

,

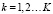где Ik – набор индексов

.

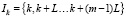Шаг 3. После вычисления

,

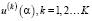определяется среднее значение:

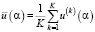. (13)

Шаг 4. Используя методы одномерной минимизации, вычисляем точку минимума αU функционала (13), и это значение примем за оценку для оптимального параметра 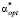, который минимизирует ошибку сглаживания

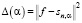(14)

конкретной одной реализации измеренного сигнала .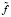

Перейдем к выбору параметра сглаживания на основе метода L-кривой, который используется в алгоритмах регрессионного анализа [11] и решения некорректных задач [12]. Введем в рассмотрение два функционала:

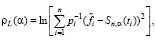
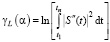, (15)

которые можно рассматривать как координаты некоторой параметрической функции (названной L-кривой) в декартовой системе координат. Кривизну этой функции определим как

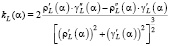. (16)

В качестве оценки для оптимального параметра αopt в методе L-кривой принимается значение αL, вычисленное из условия максимума кривизны kL(α). Для упрощения вычисления значений kL(α) предлагается первоначально на некотором множестве значений 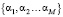вычислить величины 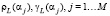, а затем по этим данным построить интерполяционные сплайны, по которым вычислить производные, входящие в (16).

Из описания этих двух алгоритмов выбора параметра сглаживания видно, что оба алгоритма не требуют задания дисперсии шума измерений, но требуют решения соответствующих оптимизационных задач, что приводит к дополнительным вычислениям по сравнению с выбором параметра при известных дисперсиях шума измерений.

Результаты исследования и их обсуждение

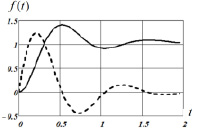
Для исследования оптимальных свойств оценок αU , αL был выполнен обширный вычислительный эксперимент. Остановимся только на некоторых результатах. В качестве тестовых сигналов были приняты два типичных для задач непараметрической идентификации, но разных по спектру: сигнал 1 – изображен сплошной кривой на рис. 1 и сигнал 2 – показан штриховой линией. Точные значения сигнала, вычисленные в узлах 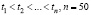, искажались случайными нормально распределенными погрешностями с относительным уровнем

.

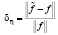При этом значения шума измерения были: а) не коррелированы между собой, б) коррелированы с значениями выборочной корреляционной функции R(0) = 1, R(1) = 0.678, R(2) = 0.421, R(3) = 0.121 (сильно коррелированный шум). Относительная ошибка сглаживания определялась выражением

.

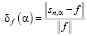Для исследования оптимальности значений параметров сглаживания αU , αL были определены соответствующие коэффициенты эффективности:

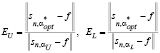. (17)

Очевидно, что чем ближе значения этих коэффициентов к 1, тем меньше проигрыш по точности соответствующего параметра сглаживания по сравнению с 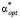. Так как эти коэффициенты являются случайными величинами, то по выборке объемом 200 вычислялись их числовые характеристики: средние значения 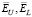и минимальные значения .

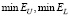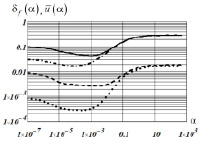
Начнем с рассмотрения свойств оценки αU. На рис. 2 показаны графики следующих зависимостей: сплошная – относительная ошибка 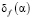при 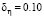; штрих-точечная – 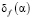при 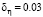; штриховая – 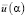при 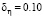; точечная – 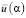при .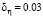

Видно, что значения αopt находятся в области минимума функционала 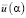, но наличие плоского участка на графике 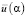усложняет процедуру минимизации 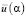. Заметим, что при уменьшении уровня шума наблюдается смещение αopt, αU в меньшую сторону. В табл. 1 приведены характеристики , .

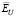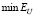Видно, что в случае коррелированного шума эти характеристики ухудшаются, особенно при большом уровне шума измерения и низкочастотном сигнале 1. Точностные характеристики 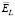, 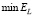метода L-кривой приведены в табл. 2. Также заметно их ухудшение в случае коррелированного шума, но не столь значительное, как в методе перекрестной значимости (табл. 1).

Для сравнения в табл. 1 и 2 жирным шрифтом выделены ячейки с наибольшим средним значением коэффициента эффективности из этих двух алгоритмов выбора параметра сглаживания. Видно, что алгоритм выбора, основанный на методе L-кривой, в большинстве случаев имеет более высокие точностные характеристики.

Таблица 1

Таблица 2

Заключение

Построенные в данной работе на основе методов перекрестной значимости и L-кривой алгоритмы могут успешно использоваться для оценивания оптимального параметра сглаживания СКС в случае некоррелированного шума измерений. Оба эти алгоритма не требуют априорной информации о величине дисперсии шума измерения. В случае коррелированного шума измерения предпочтение следует отдать алгоритму на основе метода L-кривой. Худшие точностные характеристики метода перекрестной значимости можно объяснить тем, что медленное изменение амплитуды коррелированного шума воспринимается алгоритмом выбора как некоторая составляющая «точного» сигнала, и для ее сохранения алгоритм вычисляет заниженное (по сравнению с оптимальным) значение параметра сглаживания.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-38-90041. Acknowledgments: The reported study was funded by RFBR, project number 20-38-90041.

Библиографическая ссылка