Методы оптимизации и их алгоритмизация, заключающиеся в поиске экстремума функции при наличии ограничений или без ограничений, широко используются для решения научных, технических, технологических и ряда других актуальных задач, где требуются оптимальное проектирование и разработка различных объектов (например, выбор наилучших номинальных технологических режимов, структуры технологических цепочек, условий экономической деятельности, повышение доходности и т.д.) [1, 2].
Разработка и производство любых часовых механизмов (ЧМ) представляют собой целенаправленный процесс. Эти цели определяют вид и тип ЧМ, их показатели качества, характеристики, стоимость комплектующих изделий, их изготовление и т.д. [3, 4]. Для оценки степени достижения целей, преследуемых при разработке и изготовлении ЧМ, целесообразно ввести определенную меру – целевую функцию. Часы или часовые механизмы будут называться оптимальными, если они обладают такими показателями качества, при которых соответствующая целевая функция в общем случае достигает экстремума (максимума). Таким образом, оптимизация ЧМ сводится к поиску набора показателей качества или параметров ЧМ, максимизирующих целевую функцию.
С общих метрологических позиций задача количественной оценки качества ЧМ может быть сформулирована как задача количественного сравнения объектов, определенных списочными описаниями, решаемая с помощью средств информационных технологий. С позиций предлагаемой математической модели качество ЧМ может рассматриваться как некоторая точка n-мерного гиперпространства натуральных показателей качества K1, K2, K3,…, Kn, взвешенных весовыми коэффициентами X1, X2, X3,…, Xn, учитывающими важность каждого из этих показателей. Данная точка k может быть задана координатами (K1, K2, K3,…, Kn) или радиус-вектором:
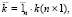(1)
где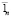 
– единичный радиус-вектор в выбранном базисе, равный сумме базисных ортов:
;
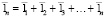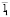– радиус-вектор точки (1, 0,…, 0);
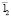– радиус-вектор точки (0, 1,…, 0) и т.д.
Исходя из выражения (1) обобщенный показатель качества ЧМ может быть представлен в матричной форме:
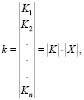(2)
где |K| – матрица-столбец натуральных показателей качества ЧМ;
|X| – диагональная матрица весовых коэффициентов, нормированных условием вида:
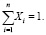
При выборе метрики вида:
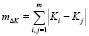
обобщенный показатель качества ЧМ можно представить в виде:
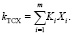(3)
Следовательно, задача количественной оценки качества ЧМ сводится к определению показателей Ki и весовых коэффициентов Xi, отражающих удельный вес потребительских свойств ЧМ. В общем случае элементы матрицы (2) могут представлять не только единичные взвешенные показатели качества, но и целые группы однотипных показателей. Групповая матрица технических показателей может быть представлена следующим образом:
(4)
При всех изменениях требований наиболее стабильной по значимости является групповая матрица технических показателей, удельный вес которой среди всех групповых матриц достаточно высок и определяется значением Xi.
Если при оценке качества ЧМ учитывать только технические характеристики, то обобщенный показатель качества можно представить в виде:
kЧМ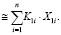
(5)
Постановка задачи
На множестве показателей качества К1, К2, К3 …,Кn , на котором задана вещественная функция цели Ц = Ц (К1, К2, К3 …,Кn), имеющая смысл того или иного показателя качества и стесненная ограничениями вида:
З (К1, К2, К3 …,Кn) < Здоп,
требуется определить оптимальный набор натуральных показателей качества Копт, максимизирующий целевую функцию Ц и одновременно удовлетворяющий введенным ограничениям величин К1, К2, К3 …,Кn .
Методы оптимизации качества ЧМ и их алгоритмизация
Учитывая выражение (4), запишем некоторую вещественную целевую функцию в виде:
Ц = Ц (К1, К2, К3 …,Кn ) =
= Ц{K1(k11,…,k1n),…,Kn(k11,…,k1n)}, (6)
для которой требуется найти оптимальный набор параметров kiОПТ, соответствующий экстремуму, максимуму или минимуму целевой функции и удовлетворяющий ограничениям вида Yi = (k11,…,k1n) > 0.
Поскольку в общем случае целевая функция может иметь несколько максимумов и минимумов, из которых нас интересует глобальный, то условие экстремальности можно записать в следующем виде:
Ц(k1ОПТ,…,knОПТ) = supЦ(k11, k12…,k1n) (7)
(kiОПТ)∈Гlim,
где Гlim – область допустимых значений ki, удовлетворяющих введенным выше ограничениям.
Методы решения такой задачи, относящейся к задачам аналитического программирования (планирования), имеют много общего с классическими методами решения оптимальных задач, но отличаются от них наличием дополнительных ограничительных условий. Поэтому можно записать условие экстремума в виде:
gradЦ(R(k)) = ∇Ц(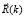
= 0, (8)
где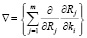 
, (i = 1,…, n) – дифференциальный оператор Гамильтона,
R = 
(9)
Выражение (8) представляет собой систему алгебраических уравнений с n неизвестными ki
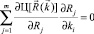(i = 1,…,n). (10)
Решение системы уравнений (10) – это значения (ki)1,…, (ki)z, которые определяют экстремальные наборы параметров, соответствующие нулям функции gradЦ(R(k)) и экстремумам функции цели, при этом z – число решений. Определяя для этих наборов параметров значения функций Yi, можно выделить из z экстремальных наборов параметров экстремальные наборы (ki), удовлетворяющие заданным ограничениям. При этом оптимальный набор параметров kОПТ может быть выбран из ki как набор, обеспечивающий наибольший из локальных максимумов или наименьший из локальных минимумов функции цели и удовлетворяющий условиям глобального экстремума. На практике целесообразно использовать различные методы оптимизации, относящиеся к специальным поисковым методам оптимизации [5, 6]. Смысл этих методов состоит в целенаправленном переборе возможных параметров ЧМ, максимизирующих целевую функцию. Фрагмент графической схемы алгоритма [7, 8] применения этих методов приведен на рисунке.
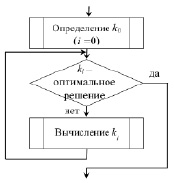
Фрагмент графической схемы алгоритма определения параметров ЧМ
Выбирается k0 – начальный набор параметров ЧМ. Строится последовательность k0, k1…,ki, при этом точки с большими номерами дают лучшее приближение к kОПТ. Необходимо учитывать, что шаг поиска, т.е. переход от ki к ki+1, состоит из выбора направления поиска, определяемого некоторым вектором F(ki), и подъема или спуска по этому направлению.
Определение точки ki+1 происходит в соответствии с выражением:
ki+1 = ki + aiF(ki),
где значение ai(ai > 0) характеризует принятый способ спуска.
Применим один из поисковых методов оптимизации, а именно градиентный метод, для решения поставленной выше задачи. С помощью градиентного метода осуществим поиск глобального экстремума функции цели, определяющего оптимальный набор параметров ЧМ kОПТ.
Поиск начинается с выбора произвольного набора параметров k0. Затем после вычисления соответствующего значения функции цели Ц = Ц(k0) ищется следующее направление скорейшего возрастания этой функции:
∆k = k – k0.
Разложим функцию цели в ряд Тейлора по приращениям ∆k в окрестности начальной точки k0.
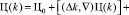
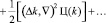
и найдем основную составляющую приращения этой функции:
∆Ц = Ц(k) – Ц0 = [(∆k, ∇)Ц(k)] +⋯
Очевидно, что максимальное значение приращения функции ∆Ц будет иметь место при совпадении направления ∆k с направлением градиента функции цели в начальной точке k0, т.е. должно выполняться условие:
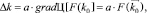
где a – коэффициент пропорциональности.
Оптимальное значение этого коэффициента получаем из условия максимума Ц(k), ограничиваясь первыми тремя членами полученного выше разложения. Подставляя в это разложение полученное значение ∆k, дифференцируя полученное выражение по a и приравнивая производную к нулю, получаем следующее выражение:
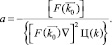
Подставляя с учетом полученного выражения величину aF(k0) в выражение для ∆k, находим новый набор параметров, более близкий к максимуму:
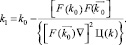
Повторяя эти шаги итеративно достаточное число раз, находим последовательно наборы параметров ЧМ, подводящие к локальному экстремуму целевой функции. Для нахождения всех z экстремальных точек (экстремальных наборов параметров ЧМ) необходимо задавать достаточно плотный ряд начальных точек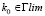 
и затем, сравнив найденные локальные экстремумы, выбрать глобальный, соответствующий набору параметров kОПТ. Преодоление этих трудностей связано с использованием дополнительных методов: Лагранжа, штрафных функций, Куна–Таккера и т.д. [9, 10].
Сложность задачи сравнительной оценки различных методов оптимизации заключается в том, что она представляет собой задачу общей теории эффективности – задачу оценки степени соответствия объекта (метода и алгоритма оптимизации) его целевому назначению.
Выводы
1. Систематизированы вопросы, связанные с алгоритмизацией методов оптимизации качества часовых механизмов, устанавливающих в процессе разработки и изготовления ЧМ оптимальный набор их показателей качества.
2. Показано, что выбор различных методов оптимизации (аналитических, поисковых и т.д.) зависит от описанных в статье условий.
3. Применение современных методов оптимизации для решения поставленных в статье задач является чрезвычайно трудоемким занятием без использования современных компьютерных и информационных технологий.
Библиографическая ссылка
Яшин В.Н., Халикова Е.А. АЛГОРИТМИЗАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ КАЧЕСТВА ЧАСОВЫХ МЕХАНИЗМОВ // Современные наукоемкие технологии. – 2021. – № 6-1. – С. 114-117;URL: https://top-technologies.ru/ru/article/view?id=38707 (дата обращения: 23.11.2024).