Разработка специализированных реконфигурируемых многопроцессорных систем (СРМС) требует значительных временных и ресурсных затрат. В последнее время, благодаря возможностям современных информационных технологий, все чаще применяются методы аналитического и численного моделирования для исследования характеристик и проектирования узлов СРМС. В данной области актуальным является исследование вероятностно-временных характеристик подсистем «процессор-память», потому как временные задержки, возникающие на этапах обмена данными между процессорными узлами (ПУ) и модулями оперативной памятью (ОП), значительно влияют на время обмена и пропускную способность подсистемы «процессор-память», что в свою очередь сказывается на производительности СРМС в целом. Следовательно, на основе методов математического и численного моделирования можно проанализировать вероятностно-временные характеристики различных архитектур подсистем «процессор-память», для того чтобы найти способы уменьшения значений временных задержек, что впоследствии позволит увеличить пропускную способность подсистемы «процессор-память».
В работах, таких как [1–3], исследование методов аналитического и численного моделирования многопроцессорных систем (МПС) и СРМС базируются на теории массового обслуживания (ТМО), где исследуются системы массового обслуживания (СМО), в которые поступает входной поток запросов в определенные моменты времени. При моделировании МПС или СРМС СМО выступают в качестве отдельных узлов МПС, а входным потоком являются, например, запросы от процессоров в ОП. Основными характеристиками СМО, которые важны для анализа СРМС или МПС, являются: число обслуживающих устройств, поток запросов, распределение времени обслуживания, длина очереди, среднее время ожидания и пребывания в очереди.
Обычно в подсистеме «процессор-память» необходимо, чтобы некоторые запросы от процессора в память обрабатывались быстрее, чем другие, например, запросы на запись должны быть обработаны сразу после того, как поступили в подсистему [4]. Цель данной работы заключается в исследовании подсистемы «процессор-память» типа UMA (Uniform Memory Access – однородный доступ к памяти), в которую поступает входной поток на обработку с относительными приоритетами.
Как описано ниже, подсистема «процессор-память» представляется в виде сети массового обслуживания (СеМО), в которой имеются как одноканальные, так и многоканальные СМО. В случае одноканальных СМО получить вероятностно-временные характеристики мы можем с помощью аналитических методов моделирования [5], однако, для многоканальных систем применение аналитических методов требует сложных, громоздких описаний и вычислений, что не всегда гарантирует точность полученных результатов. Исходя из этого, и проанализировав ряд источников [6,7], авторы пришли к выводу, что необходимо провести исследование подсистемы «процессор-память», как многоканальной СМО, на основе численных методов моделирования.
Таким образом, в работе поставлена задача, провести исследование подсистемы «процессор-память» типа UMA, путем применения аналитического и численного методов моделирования, чтобы оценить вероятностно-временные характеристики подсистемы «процессор-память», c поддержкой режима расщепления транзакций чтения и записи.
Материалы и методы исследования
Исследуемая модель подсистемы «процессор-память» представлена на рис. 1 в виде разомкнутой СеМО, на вход которой поступает суммарный неоднородный поток запросов Λ, состоящий из потоков Λ0 (от процессорных узлов (ПУ)) и Λ3 (от буфера чтения).
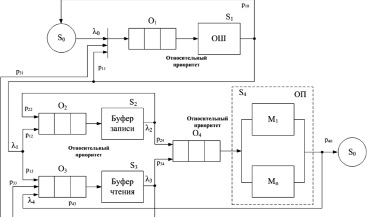
Рис. 1. Разомкнутая сеть массового обслуживания для моделирования подсистемы «процессор-память» типа UMA с приоритетным обслуживанием
Запросы на чтение и запись генерируются источником S0, моделирующим функционирование ПУ, и приходят на обработку в общую шину (ОШ) (система S1). После обработки запросы с интенсивностью Λ1 поступают в контроллер памяти, который разделяется на два обслуживающих устройства S2 (буфер записи (БЗ)) с вероятностью перехода p12 и S3 (буфер чтения (БЧ)) с вероятностью перехода p13. В итоге в зависимости от типа буфера на вход многоканальной СМО S4, представляющей собой ОП с модулями M1,…, Mn, поступают два потока Λ2 и Λ3 с вероятностями перехода p24 и p34 соответственно. Запрос, прошедший обработку в общей памяти, покидает систему S4 с вероятностью p40, либо если производится операция чтения, то запрос из общей памяти поступает с интенсивностью Λ4 в буфер чтения с вероятностью перехода p43. Далее из буфера чтения запрос с вероятностью перехода p31 поступает в общую шину, а оттуда в процессорные узлы с вероятностью перехода p10.В данной статье предлагается использовать численный метод на основе инвариантов отношений [7]. В ТМО инварианты – это соотношения, представляющиеся определенным числом начальных моментов распределений. Исходя из этого, применяются инварианты отношения, основанные на условных пропорциях для предполагаемых усредненных значений. Тогда для приведенного численного метода предлагается выполнять расчеты распределений с коэффициентом вариации ν, в пределах больше и меньше единицы. Таким образом, для данного случая, при вычислении бесприоритетных систем M/G/1 и M/G/n, включающих неоднородный поток, необходимо рассчитать суммарную интенсивность потока запросов и средневзвешенные моменты распределения обслуживания.Исходя из описания СеМО, которая является моделью подсистемы «процессор-память», для расчета вероятностно-временных требуется определенные доработки численного метода на основании инвариантов отношений, что позволит произвести вычисление времени обмена в подсистеме, в которой учитываются относительные приоритеты.Представим алгоритм действий для вычислений вероятностно-временных характеристик многоканальной приоритетной СМО, с помощью численного метода инварианта отношений. В первую очередь необходимо количество каналов умножить на быстродействие одного канала, что позволит узнать быстродействие подобной многоканальной систем.Затем требуется выполнить расчет моментов {ωi,j} распределения времени ожидания в многоканальной СМО для всех типов запросов i, и порядка моментов 
. Параметры суммарных потоков по указанным классам вычисляются согласно [7], но с некоторыми уточнениями, что соответствует исследуемой модели подсистемы «процессор-память» представленной на рис.
.
:
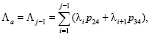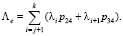(1)При этом средневзвешенные начальные моменты m-го порядка основного времени обслуживания находятся по следующим формулировкам
:
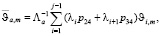
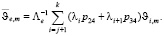(2) Следуя из теоретических описаний по относительным приоритетам [7], сформулируем выражение для вычисления моментов распределений времени ожидания в очереди
:
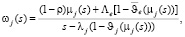(3)где ρ – загрузка СМО запросами до j-го типа включительно и выражается в данном случае как
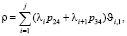
(4)μj(s) – распределение времени, когда запрос поступает на обработку в СМО и до его выхода из системы
:
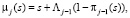(5)где πj(s) – распределение непрерывной занятости СМО запросом j-го класса, а также более приоритетным. Представим его как πj,i(s) – цикл занятости СМО, тогда, если ввести допущение, что данный цикл начался с i-запроса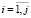 
, получим
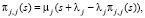
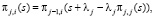
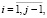
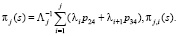
(6)Следующим этапом расчета с помощью инвариантов отношений является вычисление, по средневзвешенным моментам обслуживания и суммарной интенсивности входного потока Λ, стационарное распределение количества запросов
:
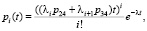
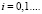(7)и среднее число запросов в очереди для одноканальной
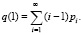СМО:
(8)Для многоканальной системы также вычисляются стационарные распределения числа запросов по формуле (7), и при таких же параметрах интенсивностей и моментов распределения обслуживания вычислить среднюю длину очереди
:
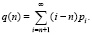(9)Затем необходимо пересчитать моменты распределения времени ожидания в многоканальной приоритетной системе для всех i
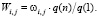j:
(10)Получив требуемые вероятностно-временные характеристики исследуемой подсистемы «процессор-память», подставим их в выражение времени обмена
:
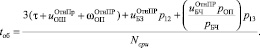(11)где τ – время выставления адреса\данных на ОШ процессором, определяется согласно типу организации управления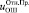 
ОШ, – среднее время пребывания в СМО «общая шина», – среднее время ожидания в СМО оперативная память определяемая из (12), – среднее время пребывания в СМО «буфер записи», p12 – вероятность того, что выполняется запрос на запись, – среднее время пребывания в СМО «буфер чтения», p13 – вероятность того, что выполняется запрос на чтение, pОП – вероятность того, что информация на чтение размещается в общей памяти, pБЧ – вероятность того, что информация на чтение размещается в БЧ, Ncpu – число процессорных узлов в МПС или СРМС.
Результаты исследования и их обсуждение
Перейдем к описанию проведенного вычислительного эксперимента с помощью разработанных методов аналитического и численного моделирования. Для сравнительного анализа результатов и проверки на адекватность разработанных методов, также было выполнено моделирование исследуемой подсистемы «процессор-память» с помощью базового метода моделирования, который основан на том, что характеристики СМО имеют следующие параметры: простейший входной поток, экспоненциальное время обслуживания, очереди без ограничения на число мест, а также бесприоритетная дисциплина обслуживания.
Задаваемые характеристики модели, представленной на рис. 1, такие как входящий поток запросов от процессоров, среднее время обслуживания в оперативной памяти, число процессоров и модулей ОП, для базового метода так и для разработанного метода одинаковы. Однако в базовом методе число мест в очередях перед общей шиной, буферами записи и чтения, а также перед оперативной памяти неограничены, и бесприоритетное обслуживание в СМО. В предлагаемом методе во всех СМО очереди являются ограниченными, а обработка производится в соответствии с дисциплиной обслуживания с относительными приоритетами.
Для получения результатов времени обмена приближенных к реальным МПС или СРМС, задаваемые характеристики брались на основании аналогичных характеристик существующих устройств. Интенсивность входящего потока запросов от процессорных узлов изменялась от 0,0114 до 0,0912 запросов/нс, что соответствовало увеличению числа процессоров от 2 до 16. Данные значения получены исходя из описания на процессорные ядра NIOS II, с рабочей тактовой частотой 50 Гц [8]. Средние времена обслуживания СМО рассчитывались в соответствии с типом устройства, которое моделировалось, следовательно, для базового метода: ϑОШ = 20 нс, ϑБЧ = 10 нс, ϑБЗ = 10 нс. Для разработанного метода ϑОШ = 14 нс (следуя из описания шины Avalon [9]), ϑБЧ = 10 нс, ϑБЗ = 10 нс. Как отмечалось выше, число мест в очередях для базового метода неограниченно. Для разработанного метода приняты следующие параметры: в ОШ – 1 место, в БЧ – 20 мест, в БЗ – 10 мест и в ОП на каждый модуль приходится по 1 месту. Число модулей памяти варьировалось от 2 до 16. Результаты расчетов вероятностно-временных характеристик изображены в виде графиков зависимостей от числа процессорных узлов на рис. 2 и 3.
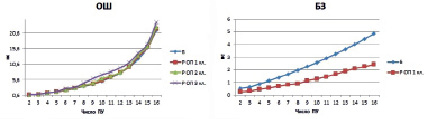
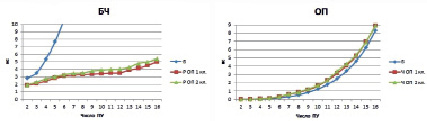
Рис. 2. Зависимость среднего времени ожидания в очередях приоритетных систем массового обслуживания подсистемы «процессор-память» от числа процессорных узлов
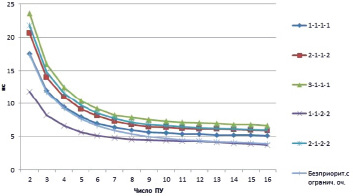
Рис. 3. Зависимость времени обмена процессора в память приоритетной и бесприоритетной дисциплины обслуживания подсистемы UMA от числа процессорных узлов
На графиках приняты следующие обозначения: базовый метод моделирования – Б, аналитический метод моделирования 1 класс (2 класс, 3 класс) – Р ОП 1 кл., Р ОП 2 кл., Р ОП 3 кл., численный метод моделирования с относительным приоритетом 1 класс (2 класс) – Ч ОП 1 кл., Ч ОП 2 кл.Согласно представленным графикам можно сделать выводы о том, что чем выше класс приоритета, тем меньше среднее время ожидания. При этом значения результатов разработанного и численного остаются в приемлемых пределах 25 нс. Результаты базового метода не могут отразить, как меняется среднее время ожидания при неоднородном потоке обслуживания, что может сказаться при точности вычисления времени обмена. При этом от 6 процессорных узлов система уходит в перегрузку, как это видно на графике среднего времени ожидания БЧ.По выражению (11) вычисляем время обмена (рис. 3) между процессором и общей памятью в подсистеме типа UMA. Во время выполнения эксперимента и в соответствии с описанием на классы приоритетов, вычислялись различные комбинации приоритетов:
- ОШ 1 кл., БЗ 1 кл., БЧ 1 кл., ОП 1 кл. на графике 1-1
-1-1;- ОШ 2 кл., БЗ 1 кл., БЧ 1 кл., ОП 2 кл. на графике 2-1
-1-2;- ОШ 3 кл., БЗ 1 кл., БЧ 1 кл., ОП 1 кл. на графике 3-1
-1-1;- ОШ 1 кл., БЗ 1 кл., БЧ 2 кл., ОП 2 кл. на графике 1-1
-2-2;- ОШ 2 кл., БЗ 1 кл., БЧ 2 кл., ОП 1 кл. на графике 2-1
-2-1;
Приведенные графики показывают, каким образом изменяется время обмена при наращивании числа процессоров, т.е. чем больше процессоров, тем меньшее время затрачивается на обмен данными одного процессора. Данное обстоятельство означает, что выполнение программы на МПС или СРМС распараллеливается на имеющееся число процессоров и модулей ОП. Также по графику можно проанализировать, как влияет обслуживание с относительными приоритетами, а именно введение различных классов приоритетов, что дает более полную картину моделирования подсистем «процессор-память».
Выводы
В статье представлен численный метод моделирования на базе ТМО и инвариантов отношений, для получения вероятностно-временных характеристик подсистем «процессор-память» СРМС. Модифицированный численный метод, предложенный в работе, позволяет получить характеристики многоканальных СМО с дисциплиной обслуживания относительных приоритетов. Как показали результаты экспериментов, характеристики, полученные с помощью инвариантов отношений, показывают наиболее полные и точные значения средних времен ожидания и пребывания в СМО, которые описывают поведение узлов подсистемы «процессор-память».Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-37-90093.
Библиографическая ссылка
Мартенс-Атюшев Д.С., Мартышкин А.И. ПРИМЕНЕНИЕ И СОВЕРШЕНСТВОВАНИЕ ЧИСЛЕННОГО МЕТОДА МОДЕЛИРОВАНИЯ ПОДСИСТЕМ «ПРОЦЕССОР-ПАМЯТЬ» НА БАЗЕ СЕТИ МАССОВОГО ОБСЛУЖИВАНИЯ С ОТНОСИТЕЛЬНЫМИ ПРИОРИТЕТАМИ // Современные наукоемкие технологии. – 2021. – № 6-1. – С. 61-66;URL: https://top-technologies.ru/ru/article/view?id=38698 (дата обращения: 24.04.2024).