Распределение концентрации удовлетворяет уравнению [1]
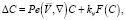 (1)
(1)
где число Пекле Pe = aU / D, kv – константа скорости объемной химической реакции, ∆ – оператор Лапласа. Поле скоростей 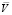 определяется [1] функцией тока ψ(r, θ). Исследуется решение уравнения (1), удовлетворяющее граничным условиям
определяется [1] функцией тока ψ(r, θ). Исследуется решение уравнения (1), удовлетворяющее граничным условиям
C = 1 при r = 1; C→0 при r → ∞. (2)
В случае, когда числа Pe, kv – соизмеримы, наиболее трудный для исследования (величина μ = kv/Pe – постоянная). Задача сводится к исследованию полулинейного эллиптического уравнения со слабой нелинейностью, величина μ = kv/Pe – постоянная. В случае F(u) ≡ u асимптотика всюду вне капли построена в работе [1].
Задача массообмена тонкой капли в протяженном потоке исследована в работе [2], а в простом сдвиговом потоке в [3], при больших числах Пекле в [4], в нелинейном объемном потоке в [5]. В случаях деформированных капель задачи тепломассопереноса исследованы в работах [6–8]. А задачам конвективного массопереноса с переменными коэффициентами посвящены работы [9–10].
Пусть функция F(u) удовлетворяет условиям
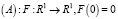 и
и 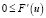 (3)
(3)
и справедливо разложение
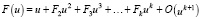 (4)
(4)
при u → 0 и для некоторого k > 1.
Уравнение (1), с учетом обозначений ε = Pe-1/2 и μ = kv/Pe, приводим к виду
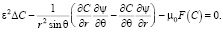 (5)
(5)
Цель исследования: построение асимптотики решения в малой окрестности капли, сначала в диффузионном пограничном слое исследуется асимптотика по малому параметру, далее вблизи точки стекания жидкости с капли исследуется асимптотика по пространственной переменной. Здесь используется техника исследования асимптотики средствами абстрактной математики в среде MAPLE и построена асимптотика на бесконечности. Далее, проводится компьютерное моделирование решений краевой задачи, используя построенную асимптотику. А затем в окрестности задней критической точки методом сращивания получен главный член асимптотики по параметру ε.
Диффузионный пограничный слой
В диффузионном пограничном слое асимптотика ищется в переменных 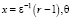 . Тогда главный член c0(x, θ) строится как решение задачи
. Тогда главный член c0(x, θ) строится как решение задачи
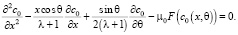 (6)
(6)
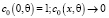 при
при 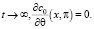 (7)
(7)
В случае, когда 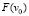 удовлетворяет условиям (3), (4), при θ → 0 для определения v0(x) получаем задачу
удовлетворяет условиям (3), (4), при θ → 0 для определения v0(x) получаем задачу
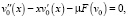 (8)
(8)
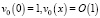 при
при 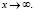 (9)
(9)
где 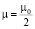 . Справедлива теорема:
. Справедлива теорема:
Теорема 1. Пусть выполнены условия (3) и (4). Тогда при x → ∞ для решения уравнения (8) справедливо асимптотическое представление
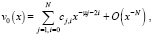 (10)
(10)
где
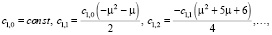
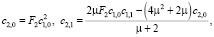
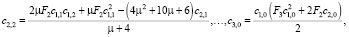
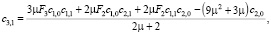
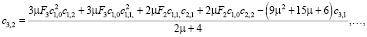
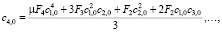
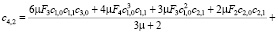
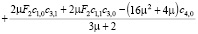 , и выполняются условия
, и выполняются условия
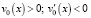 для x > 0.
для x > 0.
Доказательство теоремы. Сначала строится формальное асимптотическое решение вида (10). Для получения коэффициентов разложения применяются символьные вычисления в среде MAPLE.
Для начала в программе Maple набираем ряд для нахождения производных:
>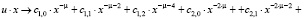
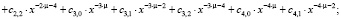
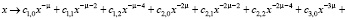
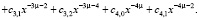
Находим производную ряда:
>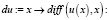
>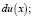
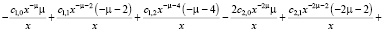
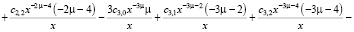
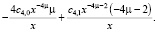
Вторая производная ряда находится:
>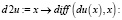
>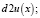
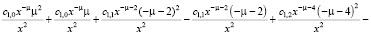
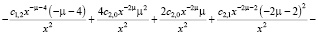
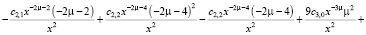
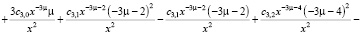
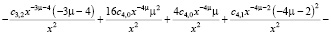
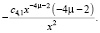
Введем повторно ряд:
>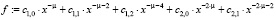
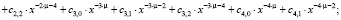
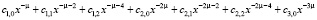
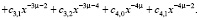
Далее возводим набранный ряд в квадрат:
>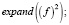
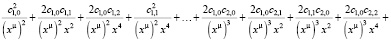
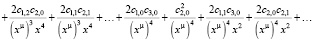
Возводим ряд в куб:
>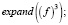
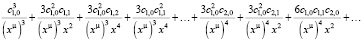
Возводим ряд в четвертую степень:
>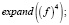
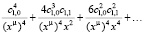
Набираем уравнение:
>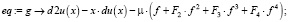
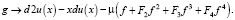
Подставляем все найденные выражения в уравнение:
>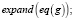
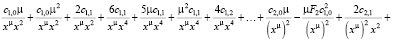
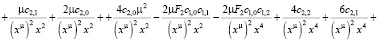
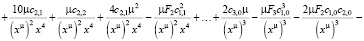
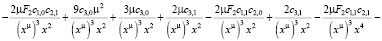
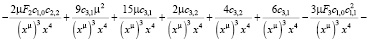
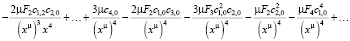
Из конечного выражения приравниваем коэффициенты при одинаковых степенях x и получаем равенства для определения коэффициентов cj,i:
>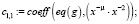
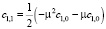
>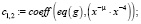
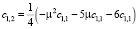
>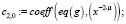
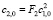
>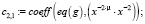
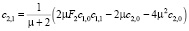
>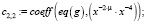
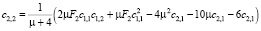
>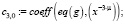
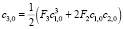
>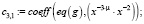
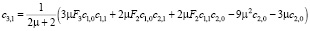
>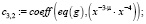
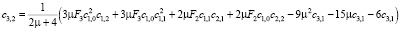
>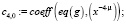
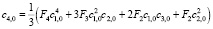
>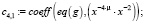
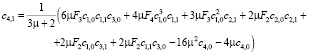
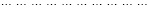
Функция v0(x) ищется в виде суммы
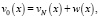 (11)
(11)
где
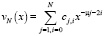 (12)
(12)
для 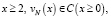
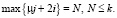
Подставляя сумму (11) в уравнение (8), мы получаем задачу
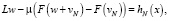 (13)
(13)
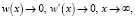 (14)
(14)
где
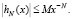 (15)
(15)
Дальнейшее доказательство состоит в следующем. Аналогично работе [11] в левой части уравнения (13) выделяем линейную часть, а нелинейную часть переносим вправо.
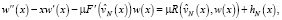 (16)
(16)
где
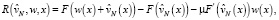
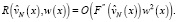 (17)
(17)
Для доказательства существования решения уравнения (16) исследуется однородное уравнение, затем задача сводится к решению интегрального уравнения.
Область задней критической точки
Решение задачи в пограничном слое задней критической точки строится в переменных 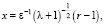
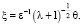 Главный член асимптотики строится как решение уравнения
Главный член асимптотики строится как решение уравнения
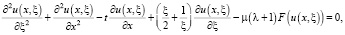 (18)
(18)
удовлетворяющее граничным условиям
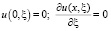 при ξ = 0 (19)
при ξ = 0 (19)
и условию согласования
u(x, ξ) – u1(x) → 0 при ξ → ∞. (20)
Функция u1(x), построенная в теореме 1, удовлетворяет всем требуемым условиям (18)–(20).
Численное моделирование
Переходим к решению краевой задачи (8), (9). Здесь следует учесть, что в полученных разложениях (10) есть произвольная константа c1,0. Для того чтобы удовлетворить первому из ограниченных условий (9), то есть v(0) = 1, применяем теорему о непрерывной зависимости решения от параметров. Уравнение (8) перепишем в виде системы
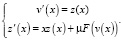 (21)
(21)
Из условий устойчивости явных схем [12] следует, что следует интегрировать назад (т.е. с шагом h < 0). Начальные условия для системы (21) имеют вид
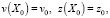 (22)
(22)
где постоянные v0, z0 определяются из выражения (10) и ее производной
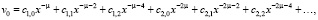
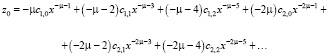
В качестве промежутка для c1,0 зададим (a, b), где, например, a = 0,01, b = 20. Далее используем цикл с предусловием. Условие для цикла задаем: |y0 – 1| > ε, где y0 = v0(0). После указываем значение x = 150 и переходим к коэффициентам, которые задаются из формулы (10), а коэффициент c1,0 находим методом половинного деления, т.е. 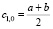 и далее уточняем приближения.
и далее уточняем приближения.
Рассмотрим случай, когда F(u) = u∙cos(u). Методом Рунге – Кутты получены следующие результаты:
μ = 0,5, y = 1,0000; z = -0,3427; c = 0,9540;
μ = 1, y = 1,0000; z = -0,6272; c = 0,9345;
μ = 3, y = 1,0000; z = -1,3495; c = 1,7560;
μ = 4,5, y = 0,9999; z = -1,7173; c = 4,6988;
μ = 5,5, y = 1,0000; z = -1,9253; c = 10,4955;
μ = 6, y = 1,0001; z = -2,0216; c = 16,2519.
Заключение
В работе показано, что в окрестности задней критической точки решение задачи существенно носит слабо нелинейный характер. Данный результат получен методом согласования асимптотики решения с асимптотикой решения в диффузионном пограничном слое.
Библиографическая ссылка
Ахметов Р.Г., Ложкина Е.В. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА МАССООБМЕНА В ОКРЕСТНОСТИ КАПЛИ С УЧЁТОМ ОБЪЁМНОЙ НЕЛИНЕЙНОЙ ХИМИЧЕСКОЙ РЕАКЦИИ // Современные наукоемкие технологии. 2021. № 6-1. С. 9-16;URL: https://top-technologies.ru/ru/article/view?id=38690 (дата обращения: 03.03.2026).
DOI: https://doi.org/10.17513/snt.38690



