Интеграция различных видов городского пассажирского транспорта в плане реализации эффективных интермодальных перевозок в настоящее время является довольно актуальной и перспективной областью исследований. Появляется много новых подходов к решению подобных проблем, которые, как правило, заключаются в сочетании и совершенствовании классических методов исследования операций.
Например, в работе [1] авторы рассматривают задачи планирования перевозок и, в частности, уделяют особое внимание интермодальным грузовым перевозкам. Описан системный подход, с помощью которого решаются проблемы мультимодальных перевозок для большой реальной компании. Подход состоит в комбинировании линейного программирования с методами планирования для получения решений хорошего качества. Предлагается новый алгоритм, объединяющий линейное программирование и оптимальное планирование, решающий возникающие в компании задачи.
В [2] разработана и реализована некоторая параметризованная модель оптимизации мультимодальной транспортировки, целью которой является оценка возможностей увеличения интенсивности работы мультимодальной транспортной службы. Для реализации модели и алгоритма оптимизации были интегрированы различные методы. Прогрессивная формулировка процесса оптимизации разработана с помощью комбинирования эволюционного алгоритма и конструктивной эвристики.
В работе [3] описывается методика количественной оценки соответствия существующей транспортной сети потребностям территории. Предлагаемый подход предлагает развитие классических результатов в данной области. В отличие от известных результатов, предлагаются количественные характеристики транспортной сети, которые используют информацию о территории с учетом ее неполноты и неопределенности. В статье также предложены показатели, которые позволяют оценить среднюю стоимость перевозки одной единицы груза по сети и относительную эффективность сети путем сравнения данной сети с сетью, в которой каждая пара вершин соединена звеном по прямой линии. Предложенные показатели учитывают неопределенность и неполноту информации о территории. Это становится возможным с помощью использования для их расчета недетерминированной матрицы корреспонденций.
Некоторое множество решений для перевозки пассажиров различными видами транспорта (трамвай, автобус, такси и индивидуальный автомобиль) рассматриваются в [4]. Проводится многокритериальная оценка вариантов, формулируется задача ранжирования по множеству критериев. Таким образом, создается последовательное семейство критериев оценки. Оно включает следующие показатели: время в пути, транспортные расходы, комфорт путешествия, надежность, своевременность, доступность, экологичность, безопасность. На основе анализа интересов построена модель предпочтений.
В рамках ранее проведенных исследований авторами [5–7] в данной работе ставится задача оптимизации маршрута поездки в условиях неопределенности.
Большинство решаемых в повседневной практике проблем в экономической сфере заключаются в множественном выборе. Среди возможных вариантов можно найти лучший, исходя из ограничений, налагаемых на природные, экономические и технологические, человеческие ресурсы. Поэтому необходимость разработки и реализации планирования и управления экономическими ситуациями с использованием математических методов исследования операций очевидна. Поиск эффективных способов планирования сложных процессов приводит к созданию модифицированных методов исследования операций. В частности, в работе представлен подход к проблеме оптимизации маршрута поездки. Рассмотрены перевозки несколькими видами транспорта. Лицо, принимающее решения, может выбрать перевозчиков исходя из информации о начальном пункте отправления, конечном пункте и доступных видах транспорта. Оптимизация процесса принятия решений осуществляется методом динамического программирования [8, 9].
Исходными данными для задачи планирования маршрутов перевозок является транспортная сеть, которая определяет географические возможности с точки зрения доступности различных пунктов отправления и назначения, оценка стоимости услуг всех возможных перевозчиков, ограничения по времени перевозки и данные о расписании маршрутных видов транспорта. Основным вопросом применения динамического программирования для решения задачи оптимального планирования поездки является возможность построения многошагового процесса принятия решений. Для разработки математической модели составной перевозки, позволяющей использовать динамическое программирование для поиска оптимального решения задачи поиска всего маршрута, необходимо описание многошагового процесса принятия решений, схема которого показана на рис. 1.
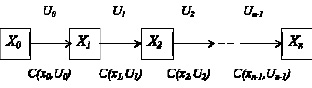
Рис. 1. Схема многошагового процесса принятия решений
Пусть система находится в начальном состоянии X0. Состояние X0 соответствует размещению пассажира в пункте отправления, а решение U0 будет означать выбор и использование конкретного вида транспорта. Цена принятия такого решения составит C(X0, U0). Далее в результате решения U0 система переходит в состояние X1. Состояние X1 соответствует завершению первой поездки. Затем в результате принятия следующего решения U1 с ценой C(X1, X1) система перейдет в состояние X2. Этот процесс будет продолжаться до конечного состояния Xn, когда пассажир достигнет конечного пункта.
Минимальная цена принятия решений за i шагов из j-го состояния описывается рекуррентным соотношением Беллмана
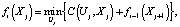(1)
где Uj – управление на j-м шаге, C(Uj, Xj) – цена принятия решения на j-м шаге. В качестве Uj реализуется выбор минимальной цены j-й перевозки.
Оптимизация многошагового процесса принятия решений
Алгоритм оптимизации построенного многошагового процесса принятия решений можно описать следующим образом.
1-й шаг. Система находится в предпоследнем состоянии Xn-1. Тогда цена принятия решения за один последний шаг составит
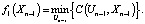
2-й шаг. Система находится в состоянии Xn-2. Тогда цена принятия решения за два последних шага составит
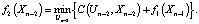
И так далее до предпоследнего шага.
(n – 1)-й шаг. Пусть система находилась в состоянии X1. Тогда цена принятия решения за три последних шага может составить одну из альтернатив
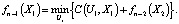
n-й шаг. Наконец, пусть система находится в начальном состоянии X0. Тогда цена принятия решения за все n шагов составит
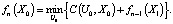
Эта цена будет соответствовать минимальной стоимости всей поездки.
Для пояснения предлагаемой методики применения динамического программирования к построению оптимальных маршрутов, включающих использование нескольких видов транспорта, можно рассмотреть модельный пример. Пусть планируется поездка из пункта A в пункт D с пересадкой двумя видами транспорта – метро и трамвай. Смена транспорта возможна в одном из двух пунктов: B или C (рис. 2).
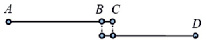
Рис. 2. Схема поездки с пересадкой
В качестве критерия оптимальности выбрано минимальное время поездки. Пусть продолжительность на участках AB, AC, BD и CD составит 30, 40, 40 и 20 мин соответственно. Схема многошагового процесса принятия решений для рассматриваемого примера показана на рис. 3.
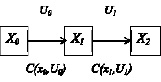
Рис. 3. Схема многошагового процесса принятия решений для двух видов транспорта
Алгоритм оптимизации построенного многошагового процесса принятия решений будет следующим.
1-й шаг. Система находится в предпоследнем состоянии X1. Тогда цена принятия решения за один последний шаг составит
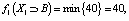
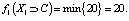
2-й шаг. Система находится в состоянии X0. Тогда цена принятия решения за два последних шага составит
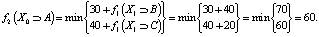
Эта цена будет соответствовать минимальному времени всей поездки, а оптимальный маршрут пройдет через пункты A → C → D.
Случай случайных параметров
Рассматривается задача динамического планирования, составленного из участков маршрута с учетом их случайного состояния [10]. Пусть весь маршрут имеет J возможных вариантов. Индексом j обозначается номер выбранного маршрута i∈J.
Если маршрут выбран, то затраты времени на прохождение j-го маршрута составят
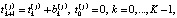(2)
где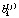 
– случайное время прохождения участка, соединяющего k-й и последующий узел j-го маршрута.
В качестве второго критерия рассматривается стоимость прохождения маршрута, которая будет складываться из цены отдельных участков
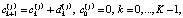(3)
где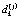 
– стоимость поездки на участке между k-м и последующим узлом j-го маршрута.
Кроме времени поездки и ее стоимости могут учитываться другие показатели прохождения маршрута, например экологический ущерб от загрязнения воздуха. В последнее время крупные пассажирские транспортные компании учитывают этот показатель.
При смене вида транспорта возможны задержки, с учетом которых уравнения (2) примут вид
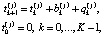(4)
где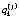 
– случайное время задержки в k-й точке j-го маршрута.
Представление стоимости и продолжительности перевозок
Введенные обозначения требуют представления исходных данных о продолжительности поездок по участкам транспортной сети в данные в виде массивов, соответствующих набору маршрутов, с учетом того, что один и тот же участок может входить в разные маршруты.
Рассмотрим более подробно формирование случайного времени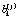 
при поездке по участку, соединяющему k-й и последующий узел j-го маршрута. Коэффициенты 
составляют матрицу B размера J×K, где J – число возможных маршрутов, K – максимальное количество участков в маршруте. Если число участков в j-м маршруте меньше Kj < K, то предполагается, что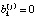 
при k = Kj + 1,..., K. Поскольку одни и те же участки входят в различные маршруты, то общее число M этих участков меньше, чем J×K. Следовательно, нет необходимости хранить J×K матрицу B, а время прохождения участка можно рассчитывать на основе вектора данных 
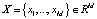о продолжительности переходов по всем M участкам транспортной сети и конфигурации маршрута. Вектор 
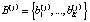, содержащий информацию о длительности перемещений по участкам маршрута, можно представить в виде
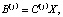(5)
где C(j) – K×M матрица, состоящая из 0 и 1 и отображающая исходную транспортную сеть в j-й маршрут.
Случайная продолжительность поездок по участкам маршрута
В случае, если решение о выборе маршрута принимается однократно, то уравнение (2) для расчета времени прохождения по маршруту можно записать в виде
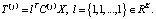(6)
Пусть xm – время поездки по m-му участку сети зависит от его состояния, то есть от случайной величины ξm, а дискретная случайная величина ξm описывает состояние сегмента маршрута, например ξm = 0, если такая поездка возможна, и ξm = 1, если поездка невозможна. Также могут быть приняты во внимание другие случайные состояния, такие как инциденты, погодные условия и т.п. На основе статистических данных можно записать изменение этой случайной величины в виде марковской цепи или задать вероятности нахождения в каждом из состояний.
Время, необходимое для прохождения участка маршрута, зависит от его состояния, но на него влияют другие факторы, как случайные, так и неслучайные. Таким образом, время транспортировки на участке записывается в виде
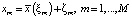(7)
или в векторной форме
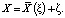(8)
Характер распределения случайных параметров
Суммарная стоимость всей поездки складывается из стоимостей услуг субперевозчиков, и незначительные колебания этих стоимостей могут существенно сказываться на общей цене. Кроме того, логично учитывать и другие факторы, определяющие разброс цены поездки. Это могут быть конъюнктура рынка перевозок, колебания цены на топливо, изменения цены в зависимости от сезона или даже времени суток и многие другие. Не говоря о редких событиях, связанных с нештатными ситуациями и форс-мажорами, влияние которых может быть достаточно сильным. Поэтому общая цена поездки является в известной степени случайной величиной. То же можно сказать и о случайном характере ее продолжительности. Но всё-таки значения этих случайных величин ограничены некоторыми конечными интервалами. Подходящее распределение для рассматриваемых случайных величин должно быть унимодальным и асимметричным. Поэтому популярные в обсуждаемой области равномерное или нормальное распределения недостаточно отражают действительность. В последнее время аналитики часто используют бета-распределение [9]. Его плотность является непрерывной унимодальной функцией с формой графика, задаваемого двумя параметрами: α и β.
Плотность бета-распределения определяется формулой
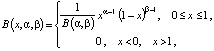(9)
где B(α, β) ‒ бета–функция.
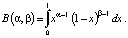(10)
Бета-распределение имеет место в случае, когда помимо наличия большого количества случайных факторов, каждый из которых в отдельности оказывает незначительное, несущественное влияние, присутствует несколько факторов, также случайных, число которых невелико, а влияние существенно [9].
Формулировка оптимизационной задачи
Если не учитывать возможность изменения решения о маршруте во время нахождения в пути, то получается задача о выборе оптимального решения в задаче стохастической оптимизации со случайной целевой функцией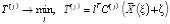 
. В соответствии с современными подходами желательно не ограничиваться оптимизацией среднего значения, а использовать квантильный критерий 
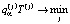, где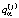 
– квантиль вероятности 1 – α для продолжительности всего маршрута 
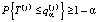. Можно также рассматривать комплекс из двух критериев.
Более интересной является динамическая постановка задачи выбора маршрута с учетом возможности изменения решения в некоторых промежуточных пунктах в зависимости от поступающей информации о состоянии транспортной сети.
В этом случае состояние участков перевозок описывается марковской цепью с непрерывным временем, а для выбора оптимального решения используется динамическое программирование.
Заключение
Использование динамического программирования для решения задач оптимизации маршрутов поездок в стохастической постановке оправдано, если применение стандартных методов является затруднительным. Кроме того, если объект исследования меняет свою структуру или характеристики, построенный многошаговый процесс принятия решений позволит оперативно корректировать алгоритм получения оптимального решения. Результаты исследования могут быть полезны для математического моделирования транспортных сетей в контексте развития и скоростного сухопутного транспорта, в частности для планирования железнодорожных пассажирских и грузовых перевозок.
Исследование выполнено при поддержке средств федерального бюджета в рамках проекта «Оптимизация транспортно-логистической системы на основе моделирования развития транспортной инфраструктуры и моделей потребительских предпочтений».
Библиографическая ссылка
Габдулхаков А.А., Завалищин Д.С. ДИНАМИЧЕСКАЯ ОПТИМИЗАЦИЯ СЛОЖНЫХ МАРШРУТОВ В ТРАНСПОРТНОЙ ЛОГИСТИКЕ // Современные наукоемкие технологии. – 2021. – № 5. – С. 33-38;URL: https://top-technologies.ru/ru/article/view?id=38654 (дата обращения: 21.11.2024).