Возрастание роли математических знаний и методов в развитии различных направлений науки, происходящие стремительные изменения в современном обществе, обусловленные его информатизацией, требуют пересмотра содержания математического образования, тщательного отбора форм, методов и средств его организации, отвечающих требованиям развивающейся науки, достижениям технического прогресса, условиям, в которых происходит организация образовательного процесса.
Реализация федеральных образовательных стандартов нового поколения по направлению «Педагогическое образование» [1], формирование российской системы непрерывного образования [2], создавшиеся ситуации, при которых вузы вынуждены переводить студентов на удаленное обучение (направление на длительную практику в связи с нехваткой учителей в отдаленных сельских школах либо отправка групп студентов на самоизоляцию в связи с массовым заболеванием), ставят задачу подготовки студента к самостоятельной внеконтактной математической деятельности. Это влечет за собой частные проблемы создания адекватных условиям методов и средств самостоятельного учения.
В современной педагогической литературе достаточно работ, посвященных определению статуса дистанционного обучения и выработке требований к его организации [3], созданию программного обеспечения для оперативного и наглядного представления учебного материала [4], разработке приемов пролонгированного учета усвоения знаний и способов деятельности по учебной дисциплине [5], созданию электронных ресурсов дидактического сопровождения управления образовательным процессом в условиях дистанционного обучения [6].
В то же время остаются открытыми вопросы: каким должно быть электронное дидактическое сопровождение каждого раздела учебной дисциплины, которым необходимо снабдить студентов очных отделений педагогических вузов с математическим профилем подготовки, переходящих временно на дистанционное обучение, позволяющее им быстро адаптироваться к новым условиям учебной деятельности? Каким требованиям должны удовлетворять его составляющие и как с его помощью студенты будут работать над усвоением математических знаний и способов деятельности?
Математические дисциплины, предлагаемые для изучения студентам педвуза, обучающимся по профилю «Математика», трудоемки и изучаются обычно в течение нескольких семестров. Поскольку студенты будут использовать сопровождающие дидактические материалы самостоятельно без непосредственного общения с преподавателем, необходимо обеспечить удобство их применения при работе над учебным материалом. Считаем целесообразным создание единого электронного ресурса для изучения каждого раздела дисциплины, содержащего в качестве компонентов дидактические материалы, помогающие студенту глубоко и осознанно усвоить теоретический материал и овладеть приемами математической деятельности, а именно: 1) осознать математическую теорию, служащую базой для овладения способами деятельности по использованию знаний при решении возникающих проблем и практических задач; 2) овладеть навыками работы с математическим материалом; 3) осознать и свободно ориентироваться в требованиях, предъявляемых к усвоению математических знаний и способов деятельности. В статье авторов [6] представлена разработанная система дидактического обеспечения управления очно-дистанционным образовательным процессом подготовки будущего учителя математики, в которой схематично обозначены структура и содержание важнейшего компонента «Электронный курс дисциплины». В силу того, что статья посвящена раскрытию управленческих аспектов использования электронного курса дисциплины, в ней не нашли отражения приемы и способы структурирования учебного материала, представления его обучающимся и организации математической деятельности с ним для достижения всех задач подготовки учителя для развивающейся современной школы и школы будущего.
Целями настоящей статьи являются: теоретическое обоснование, разработка структуры, содержания «Электронного курса дисциплины» (ЭКД), служащего первым компонентом системы дидактического обеспечения управления, ориентиром и средством организации самостоятельной деятельности по изучению программного материала изучаемого раздела дисциплины, приемов использования для осуществления самообразовательного процесса; экспериментальная проверка эффективности.
Частные задачи исследования: выявление основных компонентов ЭКД и принципов наполнения их содержанием, установление взаимосвязей между ними и выявление приемов и способов использования для организации студентом своей деятельности по выяснению сущности изучаемых понятий, методов и приемов оперирования ими.
Материалы и методы исследования
Конструирование «Электронного курса дисциплины» как средства дидактического обеспечения самостоятельной математической деятельности будущего учителя в условиях дистанционного обучения осуществлялось на следующей методологической базе:
– основных положениях системно-деятельностного, модульного подходов в образовательном процессе, разработанных И.А. Зимней [7], В.А. Хуторским [8] и М.А. Чошановым [9];
– концептуальных основах самообразования, изложенных в трудах И.Ф. Медведе- ва [10];
– технологиях и педагогических условиях разработки и использования электронных учебно-методических документов, регламентирующих деятельность студентов в условиях дистанционного обучения, выявленных в работах Е.С. Полат [3], Г.В. Лаврентьева [4], Л.А. Одинцовой и Л.М. Бронниковой [6];
– основных положениях гармонизации теоретической и практической составляющих математической подготовки будущего учителя, изложенных в трудах Г.Г. Саранцева [11].
Исходя из принятого методологического аппарата выделены критерии сформированности самостоятельной деятельности в условиях дистанционного обучения: развитая внутренняя мотивация на осуществление деятельности; самостоятельность в мышлении и деятельности, самореализация и саморазвитие; системность и систематический характер деятельности, рефлексия, самоорганизация, самообучение, самоконтроль и самооценка.
Результаты исследования и их обсуждение
Согласно методологическому аппарату исследования, в качестве основных принципов конструирования и использования электронного курса дисциплины как средства дидактической поддержки самостоятельной деятельности будущего учителя математики в условиях дистанционного обучения выбраны следующие положения:
– системности и деятельности. Создаваемый электронный курс дисциплины должен быть ориентирован на реализацию (в условиях специальной системно организованной учебной деятельности на основе выполнения сформированной системы заданий) развития умений и навыков самообразовательной деятельности обучающихся;
– модульности. Процесс усвоения студентами содержания учебного материала должен быть организован путем последовательного предъявления модулей относительно самостоятельных учебных единиц, включающих: 1) задания для проверки готовности обучающихся к усвоению знаний и способов деятельности данного модуля, мотивирующих повторительную и коррекционную деятельность, направленность на изучение нового материала; 2) теоретический материал, служащий базой освоения математической деятельности; 3) вопросы, активизирующие деятельность обучающихся по осознанию и усвоению понятий и их свойств; 4) задания на овладение приемами доказательства утверждений; 5) вопросы и задания, способствующие рефлексивной деятельности, развивающей аналитическое мышление и критическую оценку результатов своего учебного труда;
– гармонизации теоретической и практической составляющих математической подготовки будущего учителя. Организуемая самостоятельная деятельность должна способствовать гармоничному сочетанию осознанного усвоения теоретического материала (понятий и утверждений) и овладения приемами деятельности с ним;
– управляемости. Содержание электронного курса и планируемая деятельность формируются на основе анализа достигнутых обучающимися результатов предшествующего усвоения знаний и способов деятельности, полученных при проведении систематического контроля (текущего, тематического, семестрового), и осуществления коррекционной работы.
С опорой на результаты пробного педагогического эксперимента по использованию электронного курса дисциплины, изучения мнения студентов о доступности представленных дидактических материалов и удобства пользования им были внесены коррективы в содержание и структурирование электронного курса: в структуре курса выделены три блока, ее можно представить в виде схемы (рис. 1).

Рис. 1. Структура электронного курса дисциплины
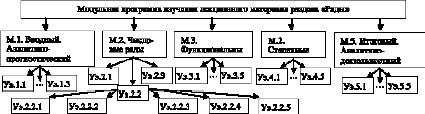
Рис. 2. Модульная программа изучения лекционного материала раздела «Ряды»
Блок 1. Электронный курс лекций, в котором представлен последовательно и четко изложенный курс лекций по изучаемому разделу дисциплины с исторической справкой, списком литературы, достаточным количеством иллюстративного материала, вопросами для самоконтроля по каждой главе.
Блок 2. Темы лекций. В нем приведены развернутые планы лекций; представлены вопросы для повторения ранее пройденного материала, инструкции, указания, схемы организации изучения понятий и теорем; выделены понятия и их свойства, на которые следует обратить особое внимание в силу сложности, трудности усвоения и важности для дальнейшего изучения дисциплины, других дисциплин учебного плана, школьной математики.
Блок 3. Модульная программа изучения лекционного материала. Теоретический материал, подлежащий усвоению, подразделяется на конечное число относительно самостоятельных модулей, взаимосвязанных, дополняющих друг друга и обеспечивающих связь учебного материала модуля с другими разделами дисциплины. Например, в разделе «Ряды» естественным образом выделяются модули: а) числовые ряды, б) функциональные последовательности и ряды, в) степенные ряды и их приложения. Но для того, чтобы нацелить обучающихся на усвоение знаний и овладение способами деятельности, формируемыми именно в этом разделе, важно в самом начале раскрыть, что будет изучаться в нем, где это пригодится при изучении математического анализа и других профильных дисциплин, какие знания и способы деятельности, освоенные ранее, будут необходимы для глубокого усвоения данного раздела. Отсюда следует необходимость включения еще двух модулей: вводного – аналитико-прогностического и заключительного – аналитико-деятельностного. Итак, модульная программа изучения раздела «Ряды» состоит из следующих модулей: М1. Вводный. Аналитико-прогностический; М2. Числовые ряды; М3. Функциональные ряды; М4. Степенные ряды и их приложения; М5. Итоговый. Аналитико-деятельностный. Последний обобщает и систематизирует изученный материал, показывает его практическую значимость.
В свою очередь, каждый из выделенных модулей делится на несколько учебных элементов. Так, модуль М1 делится на элементы: Уэ.1.1. Постановочный (выяснение роли и места раздела в структуре курса математического анализа, других профильных дисциплин, школьной математики, цели изучения); Уэ.1.2. Базово-инициирующий (выявление теоретических и практических основ его изучения, побуждение студентов путем постановки рефлексивных вопросов к самооценке достаточности своих ранее приобретенных знаний и способов деятельности для усвоения новых); Уэ.1.3. Рефлексивно-прогностический (на основе рефлексии осуществляется планирование повторения и коррекционной работы).
Модуль М2 состоит из элементов: Уэ.2.1. Повторительно-мотивирующий; Уэ.2.2. Понятие числового ряда. Основные свойства сходящихся рядов; Уэ.2.3. Положительные ряды. Признаки сходимости; Уэ.2.4. Знакопеременные ряды; Уэ.2.5. Рефлексивно-систематизирующий. Совершенно аналогично разбиваются на учебные элементы модули М3 и М4; первыми элементами в них будут соответственно Уэ.3.1. и Уэ.4.1. – Повторительно-мотивирующие, а заключительными – Уэ.3.5. и Уэ.4.5. – Рефлексивно-систематизирующие. Учебные элементы разных модулей, имеющие организационно-управляющий учебный характер, такие как Уэ.2.2, 2.3, 3.2, 3.3, 4.2, 4.3, 4.4, подразделяются (в зависимости от содержания конкретного учебного материала) обычно на 3–4 учебных элемента второго порядка, например 2.2.1, 2.2.2, 2.2.3; 2.3.1, 2.3.2, 2.3.3; и т.д. В их составе выделяются элементы следующих типов: 1) ориентационный; 2) теоретико-деятельностный, 3) практический; 4) контрольно-направляющий; 5) управленческий и самоуправленческий.
Приведем некоторые пояснения деления учебных элементов первого порядка на учебные элементы второго порядка на примере учебного элемента Уэ.2.2. Понятие числового ряда. Основные свойства сходящихся рядов. Его разбиваем на элементы второго порядка: Уэ.2.2.1. Ориентационный – позволяющий студенту понять, как на основе понятия числовой последовательности и ее сходимости формируется понятие числового ряда и его сходимости; Уэ.2.2.2. Теоретико-деятельностный – представляющий собой изложение теоретической составляющей модуля М2. Кроме введения понятий, выяснения всех существенных признаков каждого понятия, приведения примеров и контрпримеров (примеры объектов, не подпадающих под понятие), важной составляющей данного учебного элемента является обучение доказательству утверждений, основными компонентами которого служат: а) выделение условия и заключения теоремы; б) постепенное выстраивание всех этапов доказательства с иллюстрацией использования всех условий теоремы, а также известных предложений с обязательным обоснованием возможности использования в условиях данной теоремы; в) подведение итогов доказательства; Уэ.2.2.3 Практический – служит содержательной основой для формирования умений и навыков применения теоретических знаний и уже сформированных способов деятельности к доказательству утверждений и решению задач. Его содержание состоит из конкретных заданий на использование доказанных утверждений при обосновании сходимости или расходимости рядов. Путем последовательно поставленных вопросов организуется деятельность студентов по применению только что построенного фрагмента математической теории к исследованию нового объекта изучения – числового ряда. Именно этот элемент позволяет осуществлять гармоничное сочетание теоретических знаний и формирование практических умений и навыков; Уэ.2.2.4. Контрольно-направляющий элемент выполняет две функции: контролирующую и направляющую. Для реализации контролирующей функции в содержании элемента присутствуют контролирующие средства (вопросы, задачи), предъявляемые по ходу изложения материала или при подведении промежуточных итогов. В нем предусмотрены также задания корректирующего характера для исправления ошибок в усвоении учебного материала. Особенностью данного элемента является его подвижность, он может присутствовать не только в одном месте лекции, а в нескольких. Действительно, на лекции вводится обычно несколько понятий и доказываются несколько теорем, и при работе с каждым таким математическим объектом у студентов могут возникнуть проблемы усвоения; Уэ.2.2.5. Управленческий и самоуправленческий элемент представляет собой систему требований, методических рекомендаций, указаний, памяток, образцов выполнения заданий, адресованных студентам и облегчающих организацию их самостоятельной учебной деятельности по изучаемому разделу дисциплины.
Следует отметить, что в каждом учебном элементе модульной программы присутствуют задания, активизирующие деятельность студентов: 1) обозначены вопросы, на которые следует дать ответы; 2) предложено вписать пропущенные слова и словосочетания, помогающие уточнить сущность изложенного; 3) предлагается применить разобранный материал к решению задачи или доказательству утверждения; 4) предусмотрены возможные затруднения и приведены ссылки на нужный вспомогательный материал.
Настоящее исследование выполнено в качестве дополнения, уточнения, систематизации результатов изучения проблемы «Дидактическое обеспечение управления очно-дистанционным образовательным процессом по математике первокурсников педвуза», прошедшей апробацию в преподавании дифференциального исчисления функции одного переменного и его приложений, опубликованной в печати [6]. Использование разработанной схемы создания электронного дидактического обеспечения дистанционного обучения более сложному разделу математического анализа «Неопределенный интеграл» показало необходимость расширения спектра составляющих его компонентов, усиления внимания к дидактическому обеспечению усвоения теоретической составляющей математического анализа. Это повлекло за собой исследование, результаты которого представлены в данной статье.
Выводы
В результате изложенного решения проблемы усиления дидактической поддержки усвоения теоретической составляющей математической дисциплины сделаны следующие выводы.
1. Структура «Электронного курса дисциплины», служащего ориентиром и средством организации самостоятельной деятельности по изучению раздела дисциплины, должна содержать три компонента: блок 1. Электронный курс лекций; блок 2. Тематика и планы лекций; блок 3. Модульная программа изучения лекционного материала.
2. Блок «Электронный курс лекций» включает содержание теоретического материала, иллюстрации, вопросы для самоконтроля; блок «Тематика и планы лекций» – темы аннотации лекций, вопросы на повторение изученного; блок «Модульная программа изучения лекционного материала» – модули, учебные элементы, имеющие определенное целевое назначение.
3. Изучение учебного материала небольшими порциями (учебными элементами), содержащими задания, активизирующие деятельность студента на каждом этапе процесса усвоения, способствует более осознанному применению знаний к реализации различных способов математической деятельности.
4. Итоги экспериментальной проверки функционирования «Электронного курса дисциплины» в совокупности с другими средствами дидактического обеспечения при изучении разделов математического анализа «Определенный интеграл и его приложения» и «Ряды» в педагогическом вузе, подведенные с использованием статистического критерия φ* – угловое преобразование Фишера, показали существенную положительную динамику качества усвоения знаний и способов математической деятельности.
Библиографическая ссылка
Одинцова Л.А., Бронникова Л.М., Михайлова О.Ю. ЭЛЕКТРОННЫЙ КУРС ДИСЦИПЛИНЫ КАК СРЕДСТВО ДИДАКТИЧЕСКОГО ОБЕСПЕЧЕНИЯ САМОСТОЯТЕЛЬНОЙ МАТЕМАТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ БУДУЩИХ УЧИТЕЛЕЙ В УСЛОВИЯХ ДИСТАНЦИОННОГО ОБУЧЕНИЯ // Современные наукоемкие технологии. 2021. № 4. С. 207-212;URL: https://top-technologies.ru/ru/article/view?id=38641 (дата обращения: 09.02.2026).
DOI: https://doi.org/10.17513/snt.38641



