Система образования современной школы подразумевает непрерывный и всесторонний мониторинг всех составляющих ее процессов. Без внимания не должны обходиться ни основные, ни вспомогательные процессы образовательной деятельности всякого учебного заведения [1, 2]. При этом, естественно, особое внимание должно быть уделено собственно процессам обучения школьников всем учебным дисциплинам. Ввиду этого в учебном процессе необходимо использовать такие методы и средства, которые будут отвечать принципам эффективности и инвариантности их применения.
В качестве таковых функциональных инструментов можно внедрять методологии, основой которых служат методы математического моделирования различных ситуаций [3, 4]. При этом целесообразно подбирать и применять те из них, которые позволяют достигать поставленных целей на заданном временном отрезке. Иными словами, они должны выступать средством технологий обучения. Кроме того, ввиду общего направления развития образовательной сферы на цифровизацию ряда учебных процессов они должны отвечать требованиям использования информационно-коммуникационных технологий в школе.
Таким образом, необходимо, чтобы используемые методы математического моделирования выполняли функцию анализа сложившейся ситуации с известными и прогнозируемыми характеристиками. Это необходимо для принятия взвешенных оптимальных решений в режиме реального времени. Только такой подход позволит осуществить в обучении школьников в контексте непрерывного роста изучаемой информации достижение поставленных образовательных целей.
Методы математического моделирования широки и многообразны. Одни из них служат универсальным средством моделирования [5, 6], другие востребованы лишь в определенных случаях, отвечающих заданным параметрам исследования [7, 8]. Так, в ситуации диагностики знаний школьников могут быть применены те и другие методы. В то же время, безусловно, наиболее востребованы те из них, которые эффективно работают в условиях многофакторности проводимого анализа. Одним из таких подходов является использование методологии соответствия Галуа и математического аппарата импликативных матриц для мониторинга различного рода учебных ситуаций на всем протяжении учебного процесса в целом и в целях диагностики в частности.
Цель исследования – описание и анализ применения возможностей программного комплекса «Advanced Tester» как инструмента математического моделирования для диагностики знаний школьников в условиях цифровизации системы образования.
Научная новизна состоит в использовании в работе программного комплекса «Advanced Tester» для диагностики знаний школьников с помощью средств математического моделирования при организации индивидуального обучения.
Материалы и методы исследования
Диагностика учебных достижений является важным фактором как в определении целей дальнейшего обучения школьника, так и возможностей развития его способностей оптимальным образом. Своевременно оцененный уровень знаний школьника способствует наиболее точному формированию индивидуальных и групповых траекторий обучения, выбору необходимых средств и методов обучения. При этом следует подчеркнуть, что диагностика должна проводиться непрерывно на протяжении всего процесса обучения. Только в этом случае это позволит вовремя вносить при необходимости коррективы в учебный процесс, осуществляя, таким образом, его мобильность в условиях массового обучения в школе.
Теоретико-методологической основой исследования служат, с одной стороны, системный подход к организации учебно-воспитательного процесса и концепции педагогического проектирования, вопросами которых занимались Ю.К. Бабанский, В.П. Беспалько, З.И. Калмыкова, В.В. Краевский, М.В. Кларин, И.Я. Лернер, М.И. Махмутов, Н.А. Менчинская, И.С. Якиманская и др. С другой стороны, общая теория диагностических методов и концепции информатизации образования, проблемы которых решали С.А. Бешенков, Дж. Гласс, С.П. Грушевский, К.М. Гуревич, К.К. Колин, К.А. Краснянская, Б.В. Кулагин, Дж. Стенли, Е.А. Ракитина, И.В. Роберт и др.
Совокупность данных подходов является фундаментальной основой развития знаний и умений школьников с использованием возможностей информационно-коммуникационных технологий как средства цифровизации образовательной сферы. При этом для анализа уровня усвоения знаний учащихся целесообразно применять методы математического моделирования. В частности, определение ключевых факторов и латентных параметров ведения образовательной деятельности можно эффективно осуществлять с помощью методологии соответствия Галуа [9, 10] и импликативных матриц [11, 12] при принятии основополагающих решений с помощью автоматизированных программных комплексов.
Так, в контексте непрерывного мониторинга образовательной деятельности в рамках учебного процесса должна осуществляться диагностическая работа. Ее систематическое проведение невозможно без использования средств моделирования текущей ситуации и прогнозирования ее развития. В рамках проведения текущего исследования для этого использовалась методология соответствия Галуа. Она позволяет с помощью математического анализа совокупности текущих показателей выявить структурные элементы, которые оказывают существенное влияние на функционирование системы в целом либо играют решающую роль в поведении отдельных ее частей. Данная методология применялась для диагностирования знаний и умений школьников и организации их дальнейшего обучения в малых группах с вариативным составом с использованием инструментов специально разработанной для этого информационной системы «Advanced Tester» [13].
Исследование заключалось в следующем. Была выдвинута гипотеза исследования, что применение специальных методов математического моделирования с использованием автоматизированных программных комплексов для анализа уровня знаний школьников будет способствовать повышению качества их обучения. Для этого необходима текущая диагностика учебных достижений, которые могут в различной степени оказывать влияние на учебный процесс. На подготовительном этапе в среде автоматизированной информационной системы «Advanced Tester» были созданы графовые модели учебного материала по двум предметам естественнонаучного цикла дисциплин физики и информатики. Выбор учебных предметов должен был продемонстрировать инвариантность используемых методов соответствия Галуа от содержания предмета изучения в школе.
Затем был создан банк заданий различной формы и степени сложности и сопоставлен с полученными графовыми моделями и изучаемым содержанием учебных дисциплин. В системе «Advanced Tester» был сгенерирован набор тестов для входной диагностики школьников по двум предметам, а также предложены унифицированные анкеты для оценки индивидуальных запросов школьников. Дальнейшее обучение осуществлялось в соответствии с планом предметного обучения. Материал изучаемых по физике и информатике разделов был разбит на логические блоки, после каждого из которых проводилась диагностика знаний и умений школьников. Обучение, построенное таким образом, проходило в течение месяца и включало по четыре блока учебного материала в каждой дисциплине. По завершении изучения отведенных под эксперимент разделов была проведена итоговая диагностическая работа.
Особенность обучения состояла в том, что на формирование общей стратегии учебного процесса существенным образом влияло распределение обучаемых школьников по группам. Это определялось тем, что в рамках текущего изучения материала каждого блока с помощью средств автоматизированной информационной системы на основе соответствия Галуа проводилось исследование учебных достижений школьников, своевременный контроль которых оказывает существенное влияние на формирование стратегии дальнейшего обучения учащегося. Анализ проводился по разным наборам показателей с помощью математического аппарата импликативных матриц. Это позволяло выявить параметры генеральной совокупности школьников, которые на данный момент оказывают существенное влияние на характеристики всей выборки. После этого происходило формирование в соответствии с заданными параметрами и критериями обучения состава малых групп для изучения текущего вопроса учебной дисциплины. Для этого средствами информационной системы «Advanced Tester» выявлялись для каждой группы учащиеся, по характеристикам которых можно было судить о возможностях всего группового состава, прогнозировать их результаты и вести учебный процесс оптимальным образом. При этом следует отметить, что состав этих групп достаточно мобилен. При изучении следующего вопроса он мог изменяться существенным образом. Это необходимо для максимального учета индивидуальных и групповых запросов обучения и результатов диагностики учебных достижений. Оптимальный состав малых групп при такой организации обучения, как правило, составляет от четырех до восьми человек. Это позволяет наиболее эффективно распределить нагрузку учителей в рамках обучения в классе и оптимально учесть вопросы предметной подготовки и мотивированности школьников. Такое распределение на малые группы оказывается эффективно как при традиционном очном обучении, так и при дистанционных форматах обучения [14, 15]. При этом в учебном процессе обязательно должно быть отведено время как на непосредственное взаимодействие с учителем, так и на самостоятельную отработку умений и навыков. Количество того и другого времени может варьироваться, но каждое должно составлять не менее 30 % от общего времени изучения учебного материала. Степень самостоятельности при изучении может быть различной. Она зависит как от состава малых групп на общем временном промежутке, так и от сложности изучаемых школьниками вопросов.
Автоматизированная информационная система «Advanced Tester» позволяет как учителю, так и школьнику выбирать степень сложности учебного материала. При этом исходную сложность изучаемых вопросов определяет учитель в зависимости от результатов входной диагностики. Затем, в процессе обучения, сложность теоретического и практического материала может варьироваться в зависимости от результатов диагностических срезов. Здесь следует заметить, что оперировать таким объемом полученных при систематических диагностических процедурах данных учителю было бы достаточно сложно. Именно для этого ему и необходимы инструментальные математические средства автоматизированных информационных систем. Использование в них аппарата математического моделирования служит объективным средством анализа больших объемов данных. При этом особенность применения соответствия Галуа заключается в выявлении латентных параметров обучения школьников при их распределении на малые группы. Ряд факторов, влияющих на индивидуальную траекторию обучения, учитель может определить и самостоятельно. Он может делать это как интуитивно, так и с привлечением иных средств математического моделирования. В то же время математический функционал соответствия Галуа, как и некоторых других методов, позволяет по заданным критериям проверять различные гипотезы успешности усваивания учебного материала. Методология соответствия Галуа позволяет оперативно принимать решения, критичность которых зависит от временного интервала, непосредственно влияющего на эффективность выбранных методов обучения.
Результаты исследования и их обсуждение
Экспериментальная работа проводилась на базе частного образовательного учреждения «Смоленский физико-математический лицей при МИФИ» и физико-математической школе при Смоленском государственном университете. Школьники 10 и 11 классов лицея составляли экспериментальную группу, а учащиеся лицея – контрольную группу. В каждой из групп фиксировались результаты обучения физике и информатике. Количественный состав был равномерно распределен. В экспериментальную группу входили 21 десятиклассник и 19 одиннадцатиклассников МИФИ лицея. В контрольную группу – по 20 десяти- и одиннадцатиклассников соответственно.
В экспериментальной группе обучение физике и информатике проводилось с применением автоматизированной информационной системы «Advanced Tester», реализующей в виде функциональных инструментов методологию математического моделирования соответствия Галуа для формирования траектория оптимального обучения в малых группах. В контрольной группе обучение велось традиционными методами обучения с использованием возможностей информационно-коммуникационных технологий в поиске, систематизации и демонстрации учебного материала. В каждой из групп было проведено входное диагностическое исследование знаний школьников, четыре промежуточных диагностических среза и итоговая диагностическая работа. Для определения уровня знаний использовалась тестовая система оценки учебных достижений. Задача педагогического эксперимента состояла в том, чтобы показать эффективность использования методов математического моделирования для анализа уровня усвоения знаний школьниками при построении индивидуальных траекторий обучения. Для подтверждения эффективности использовались результаты проверочных работ, количественный анализ которых осуществлялся по формуле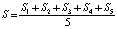 
, где S1, S2 – теоретические вопросы, а S3, S4, S5 – практические задания, оцененные по пятибалльной системе. Данные итоговой диагностики знаний и умений представлены в табл. 1 и 2 по физике и информатике соответственно.
Таблица 1
Результаты формирующего этапа эксперимента по физике
|
Группа |
Число учащихся, достигших уровня усвоения знаний |
Всего |
||
|
Высокий |
Повышенный |
Базовый |
||
|
Контрольная группа |
8 |
25 |
7 |
40 |
|
Экспериментальная группа |
15 |
22 |
3 |
40 |
|
Всего |
22 |
47 |
10 |
80 |
Таблица 2
Результаты формирующего этапа эксперимента по информатике
|
Группа |
Число учащихся, достигших уровня усвоения знаний |
Всего |
||
|
Высокий |
Повышенный |
Базовый |
||
|
Контрольная группа |
9 |
23 |
8 |
40 |
|
Экспериментальная группа |
17 |
21 |
2 |
40 |
|
Всего |
26 |
44 |
10 |
80 |
Результаты формирующего этапа эксперимента по физике и информатике отражены на рис. 1 и рис. 2 соответственно.
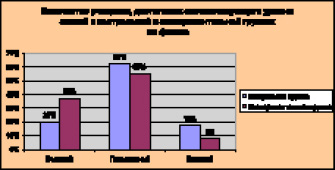
Рис. 1. Результаты формирующего этапа эксперимента по физике
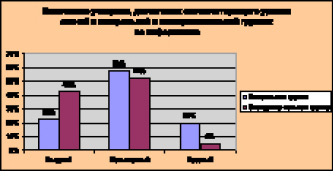
Рис. 2. Результаты формирующего этапа эксперимента по информатике
Качественный анализ условий и результатов эксперимента
Из представленных табличных данных и диаграмм видно, что количественные показатели высокого уровня в контрольной группе ниже, чем в экспериментальной группе. А показатели базового уровня, наоборот, выше. Это обусловлено, на наш взгляд, тем, что использование возможностей программного комплекса «Advanced Tester» для построения образовательных траекторий с учетом уровня индивидуальных достижений способствовало стимулированию школьников к более глубокому усвоению знаний. Тогда как в контрольной группе при отсутствии текущей диагностики снижался контроль уровня учебных достижений. Результаты обучения школьников физике и информатике свидетельствует об инвариантности используемых методов относительно предметной области учебной дисциплины. Исходя из результатов формирующего этапа педагогического эксперимента, состоящих в положительной динамике усвоения знаний школьниками при использовании методов математического моделирования с помощью инструментов автоматизированного программного комплекса «Advanced Tester» можно сделать вывод, что поставленная в ходе эксперимента задача реализована.
Заключение
В соответствии с приведенными табличными данными и данными диаграмм можно сделать вывод о необходимости применения в целях диагностики знаний и умений школьников методов математического моделирования. В частности, результаты диагностических срезов свидетельствуют о том, что уровень сформированности предметных знаний и умений выше в экспериментальных группах, как при изучении физики, так и информатики. При этом если бы исследование проводилось только по информатике, то можно было сделать вывод о косвенном влиянии ее предметной области как учебной дисциплины на использование функциональных возможностей автоматизированной информационной системы «Advanced Tester». В то же время данные по изучению физики с использованием тех же методологических подходов показывают аналогичные корреляционные зависимости. Результаты обнаруживают общие тенденции в овладении знаниями как в исследуемых группах по одной дисциплине, так и в совокупности знаний междисциплинарного характера. Таким образом, можно судить об эффективности практики применения методологии соответствия Галуа как средства диагностики знаний и умений школьников по различным учебным дисциплинам.
В завершение отметим, что практика внедрения подобных методов математического моделирования для непрерывной диагностики знаний школьников должна расширяться. Именно диагностические процедуры позволяют своевременно и объективно выявить потребности и возможности в обучении учащихся в современной школе. При этом разумное использование цифровых технологий, как и информационно-коммуникационных средств обучения, должно способствовать повышению общего уровня системы школьного образования.
Библиографическая ссылка
Козлов С.В., Быков А.А. ПРИМЕНЕНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ ДИАГНОСТИКИ ЗНАНИЙ ШКОЛЬНИКОВ // Современные наукоемкие технологии. – 2021. – № 4. – С. 157-162;URL: https://top-technologies.ru/ru/article/view?id=38632 (дата обращения: 03.12.2024).