Гидродинамическое исследование скважин является инструментом для определения фильтрационных характеристик газонефтяных месторождений. Данная информация необходима для корректного планирования работ по эксплуатации месторождения.
Прогноз распределения фильтрационных свойств нефтегазовых месторождений (углеводородов) позволяет получать гидродинамическая томография с основой на данных гидропрослушивания скважин и оценке изменения поведения реперной точки кривой восстановления давления (КВД) [1, 2].
Гидродинамическая томография позволяет получать уточненную информацию о фильтрационном сопротивлении проницаемого пласта в пространстве между скважинами. Метод гидродинамической томографии состоит в расчете интервальных времен наступления отклика в остановленных скважинах на изменение давления в нагнетающих скважинах и их анализе.
Исходные данные для метода гидродинамической томографии могут быть получены с помощью одного из перечисленных способов либо их совместного применения:
1) прямой регистрации интервальных времен наступления отклика реакции в остановленных скважинах на изменение давления в нагнетающих скважинах (при прямой регистрации изменения интервальных времен исходные данные должны быть получены с помощью эксперимента на месторождении (активная гидродинамическая томография));
2) анализа истории эксплуатации место- рождения.
При использовании метода гидродинамической томографии, основанного на анализе истории эксплуатации месторождения, исходные данные синтезируются в форме изменения по всем скважинам в пределах выбранного временного интервала: объема добываемой жидкости и нагнетания жидкости в скважину (пассивная гидродинамическая томография) [3, 4].
Активная гидродинамическая томография затратна и трудоемка. Для пассивной гидродинамической томографии требуется синтезирование данных, выполняемое на базе вычислительного эксперимента, в рамках которого используется построенная математическая модель месторождения. Таким образом, целесообразно применение пассивной гидродинамической томографии как с экономической точки зрения, так и с точки зрения трудозатрат.
Материалы и методы исследования
Задача расчета пространственного распределения фильтрационного сопротивления пласта решается с помощью вычисления последовательных приближений значений коэффициента пьезопроводности. Вычисление последовательных приближений включает решение интегрального уравнения методом итераций, описывающего динамику интервальных времен перемещения реперной точки между скважинами. Сначала задается сетка пропластка месторождения с нулевым приближением среды (распределением значения коэффициента пьезопроводности), и по заданному приближению среды рассчитываются траектории движения сигнала (реперных точек) и интервальные времена. Затем вычисляется невязка интервальных времен, полученных в процессе моделирования, и наблюдаемых интервальных времен, и рассчитывается новое пространственное распределение значений коэффициента пьезопроводности, обеспечивающее наименьшую невязку. Дальше по полученному распределению значений коэффициента пьезопроводности рассчитываются новые траектории движения сигнала и интервальные времена. Итерационный процесс продолжается до тех пор, пока невязка интервальных времен, полученных в процессе моделирования движения сигнала, и наблюдаемых интервальных времен изменения давления превышает заданное допустимое значение.
Ниже представлена вычислительная схема гидродинамической томографии. Рассматриваемый пропласток месторождения S покрывается сеткой размерами X×Y с целью дискретизации процесса. Каждая ячейка сетки характеризуется парой индексов s(i, j), где i = 1÷X, а j = 1÷Y. По всему пропластку задается нулевое приближение среды χ(s). Через пропласток месторождения проходят скважины, образующие между собой K пар – произведение количества нагнетающих скважин (M) и количества остановленных скважин, в которых ведется прием сигнала (N). Движение сигнала между скважинами осуществляется по траектории Lk = L(skm, skn), где k = 1÷K – номер пары скважин. Каждая траектория имеет начало в точке нагнетающей скважины skm и окончание в точке скважины-приемника skn. Время движения сигнала по траектории Lk обозначается tk. Координата сетки вдоль траектории Lk обозначается sk. Расстояние, пройденное сигналом от координаты skm до координаты sk по траектории Lk, обозначается l(s). Время движения сигнала tk рассчитывается по формуле:
,
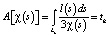которая в дискретном представлении принимает вид:
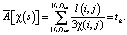(1)
Соотношение (1) позволяет рассчитать согласно принципу Беллмана кратчайшие траектории движения сигнала реперных точек с условием минимизации интервальных времен tk. В дальнейших расчетах используются рассчитанные кратчайшие траектории.
Обозначим через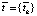 
наблюдаемое время движения сигнала, полученное в рамках истории эксплуатации месторождения. Наблюдаемое время соответствует распределению значения коэффициента пьезопроводности χ(s) + ∆χ(s). Отсюда следует задача: рассчитать ∆χ(s) такое, чтобы полученное tk минимально расходилось с 
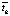. В таком случае невязка интервальных времен ∆tk рассчитывается в виде выражения:
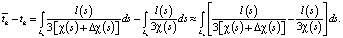(2)
Поменяв местами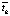 
и 
:
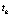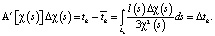(3)
Линейный оператор A'[χ(s)], действующий на вектор ∆χ(s), также является производной Фреше [5] в «точке» χ(s) к оператору A[χ(s)]. Формулы (2) и (3) основаны на допущении, что значение ∆χ(s) незначительно, поэтому траектории Lk = L(skn, skm) и произведение (χ(s) + ∆χ(s))×χ(s) ≈ χ(s)2 для пьезопроводности χ(s) + ∆χ(s) и χ(s) практически совпадают.
В дискретном представлении выражение (3) принимает вид:
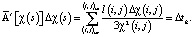(4)
Размерность вектора ∆χ(i, j) определяется в зависимости от количества ячеек в траектории: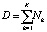 
, где Nk – количество ячеек в траектории k. Вектор ∆t = {∆tk}, имеющий размерность K, является областью значения выражения (4). После расчета вектора ∆χ(i, j) выполняется вычисление приближения коэффициента пьезопроводности:
χ2(s) = χ(s) + ∆χ(s). (5)
Вычисление выражения (4) относительно вектора ∆χ(i, j) в точках пропластка траекторий Lk = L(skn, skm) выполняется на основе итерационного метода, который на итерации z + 1 вычисляется по формуле:
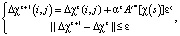(6)
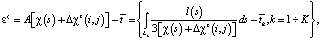
где εz – невязка интервальных времен, полученных в процессе моделирования на итерации z, и наблюдаемых интервальных времен.
В качестве нулевого приближения было принято значение ∆χ0(i, j) = 0.
αz – параметр релаксации, который подбирается на каждой итерации для обеспечения сходимости метода итераций (6) [6]:
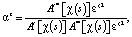
где A'*[χ(s)] – оператор, сопряженный к оператору A'[χ(s)], который вычисляется на основе условия для вектора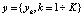 
:
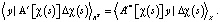(7)
В данном случае X представляет собой функциональное пространство для вычисления приращения к ∆χ(s). Данное функциональное пространство в дискретном представлении принимает вид: RD (где D – размерность вектора ∆χ(i, j), а K – размерность вектора y); тогда выражение (7):
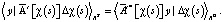(8)
Если подставить формулу действующего на вектор ∆χ(s) линейного оператора A'[χ(s)] в выражение (8), то:
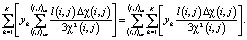
Реализация в правой части выражения суммирования привносит смысл уравнению и устанавливает вид оператора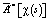 
.
Оператор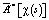 
на векторе y принимает значения вектора g(i, j) с индексами 
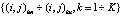. Траектории Lk, в интервалы которых попадают индексы (i, j), определяются значениями k(i, j). Таким образом, формула для расчета сопряженного оператора на векторе y:
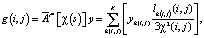(9)
где lk(i, j)(i, j) – часть траектории Lk от начальной координаты до координаты, в которой рассчитывается вектор g(i, j). При y = εz уравнение (9) принимает вид:
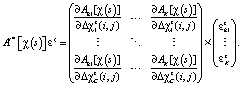
Завершением метода итераций являются выполнение условия (6) и вычисление приближения распределения значений коэффициента пьезопроводности в ячейках сетки. После завершения описанного итерационного процесса по пропластку месторождения S вычисляются новые траектории, и метод итераций повторяется.
Рассмотрим результат применения метода гидродинамической томографии для расчета коэффициента пьезопроводности по данным тестового месторождения. Исходными данными был выбран пропласток месторождения, через который проходят шесть скважин. В качестве исходных данных были заданы:
- однородная среда (рис. 1) для нулевого приближения распределения значения коэффициента пьезопроводности;
- наблюдаемые интервальные времена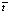 
между всеми парами скважин (K = 20).
Согласно рассмотренному методу на первом шаге вычисляются траектории, по которым осуществляется движение сигнала между скважинами, Lk, а также интервальные времена tk.
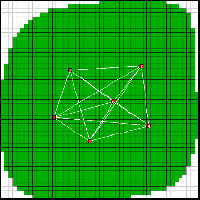
а) б)
Рис. 1. Пропласток месторождения с пятью скважинами и нулевым приближением среды (а); траектории движения сигнала между скважинами на первой итерации (б)
Здесь и далее красными кругами отображаются координаты скважины, проходящие через пропласток, белой линией – траектории движения сигнала, цвет ячеек отображает значение коэффициента пьезопроводности (чем темнее, тем больше коэффициент пьезопроводности).
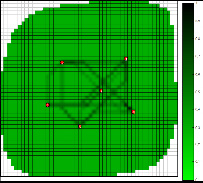
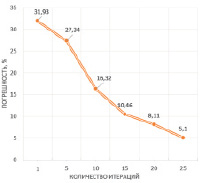
Первая итерация заканчивается расчетом ∆χ(i, j), после чего вычисляются новые значения коэффициента пьезопроводности по формуле (5) (рис. 2а). Рис. 2б отображает график изменения относительной погрешности ε наблюдаемых интервальных времен и рассчитанных на первом шаге итерационного метода (6).
а) б)
Рис. 2. Результат фильтрационного сопротивления, рассчитанный на первой итерации (а), и изменение средней относительной погрешности на первой итерации (б)
а) б)
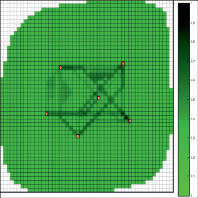
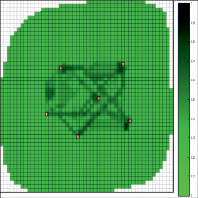
Рис. 3. Результаты фильтрационного сопротивления, рассчитанные: на второй итерации (а), на десятой итерации (б)
Результаты исследования и их обсуждение
Результаты оптимизации значений коэффициента пьезопроводности на второй и десятой итерации представлены на рис. 3а и 3б соответственно.
Изменение средней относительной погрешности по ∆t после расчета траекторий движения сигнала между скважинами по пропластку (2) представлено на рис. 4. Затем вычисляется оценка полученной величины и принимается решение о продолжении или прекращении процесса вычислений (6).
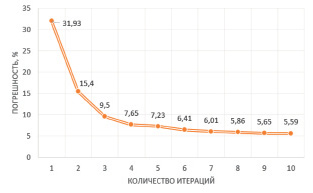
Рис. 4. Изменение относительной погрешности по ∆t
Заключение
Результат проведенного эксперимента по данным одного пропластка тестового месторождения, содержащего пять скважин, с целью проверки применимости метода гидродинамической томографии для расчета коэффициента пьезопроводности по интервальным временам наступления отклика реакции в остановленных скважинах при изменении давления в нагнетающих скважинах продемонстрировал, что описанный метод может быть использован для вычисления фильтрационного сопротивления на основе выбранного начального приближения.
Библиографическая ссылка
Кунцев В.Е., Кожевникова П.В., Дорогобед А.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГИДРОДИНАМИЧЕСКОЙ ТОМОГРАФИИ // Современные наукоемкие технологии. – 2021. – № 4. – С. 64-69;URL: https://top-technologies.ru/ru/article/view?id=38616 (дата обращения: 03.12.2024).