В последние десятилетия возрос интерес к использованию электрофизических и электрохимических методов обработки (ЭМО) с применением современных технологических схем генерации поверхности. Примерами могут служить технологические схемы электрохимической обработки, осуществляемые посредством многокоординатного движения непрофилированного (стержневого, проволочного) электрода-инструмента (ЭИ) [1–3]. Повышение эффективности практического применения данных технологий требует решения ряда оптимизационных задач, связанных с выбором параметров режима и условий обработки. Актуальной в связи с этим является задача поиска оптимальных, с точки зрения времени обработки, режимов многопроходной последовательно-строчной электрохимической обработки.
Цель исследования: разработка математической оптимизационной модели процесса последовательно-строчной многопроходной электрохимической обработки стержневым ЭИ с полусферическим рабочим торцом; использование этой модели для решения задачи оптимизации параметров режима многопроходной обработки в целях достижения минимального времени на выполнение операции.
Описание технологии и математическая модель
Обработка, снятие припуска осуществляются по технологической схеме последовательно-строчной электрохимической обработки (ЭХО) непрофилированным электродом-инструментом с полусферическим рабочим торцом [4].
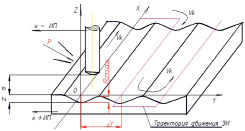
Сущность технологической схемы состоит в следующем: стержневой ЭИ с полусферическим рабочим торцом радиуса rt и изолированной державкой, соединенный с отрицательным полюсом источника питания, двигаясь со скоростью Vk по зигзагообразной последовательно-строчной траектории с шагом строк Dy и с зазором s над обрабатываемой поверхностью заготовки, соединенной с положительным полюсом источника питания, снимает слой металла – припуск z (рис. 1а). В межэлектродный промежуток (МЭП) подается электролит под давлением P.
а) б)
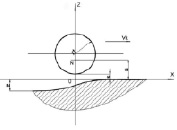
Рис. 1. Схемы обработки: а – технологическая схема последовательно-строчной электрохимической обработки поверхности электродом-инструментом с полусферическим торцом; б – расчетная схема
Для расчета поперечного профиля единичного следа z(y), который образовался при движении НЭИ вдоль прямой y = 0, z = a из минус бесконечности до точки (0, 0, a) может быть использована формула [4], рис. 1б:
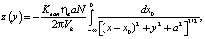 (1)
(1)
где
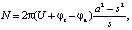 (1а)
(1а)
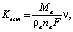 (1б)
(1б)
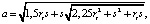 (1в)
(1в)
Ma – атомная масса металла анода, кг/моль; na – валентность металла анода; F – число Фарадея 96500, Кл/моль; ν – электропроводность электролита, См/м; ρa – плотность растворяемого материала анода, кг/м3; ηa – выход по току; a – расстояние до эквивалентного источника, м; N – интенсивность источника, Вм, рис. 1б; φc, φa – электродные потенциалы катода и анода соответственно, В.
Ранее, в работе [5], нами была проведена оценка погрешности разработанной модели, показавшая, что модель позволяет с удовлетворительной точностью описывать процессы в наиболее интересной для практической области значений технологических параметров.
Электродные потенциалы и анодный выход по току в общем случае являются функциями плотности тока. В настоящей работе мы принимаем ηa(j) = const (что допустимо при использовании хлоридного электролита), электродные потенциалы катода и анода также приняты постоянными и равными φc = 1,5 В, φa = 0,5 В [6].
Из (1) при x, стремящемся к бесконечности (рис. 1б), получим форму сечения единичного следа после полного цикла обработки:
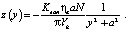 (2)
(2)
Скорость подачи электрода-инструмента Vk может быть определена из (2), если принять y = 0:
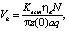 (3)
(3)
где q = 1/ftw – скважность импульсов тока (отношение периода следования импульсов к длительности импульса); tw – длительность импульса тока; f – частота следования импульсов тока.
Форму поверхности детали, возникающую в соответствии со схемой (рис. 1а) при m-строчной обработке и при условии, что сдвиг траектории на каждом шаге производится по оси y на величину Dy, можно рассчитать по формуле:
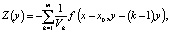 (4)
(4)
где
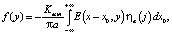 (4а)
(4а)
где напряженность электрического поля в МЭП:
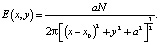 (4б)
(4б)
При суммировании от k = –∞ до k = +∞ выражение (4) может быть преобразовано в вид:
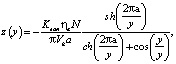 (5)
(5)
Из (5) может быть получена формула для расчета высоты гребешка Rmax (рис. 1а), образующегося при наложении двух соседних строк в зависимости от шага строк Dy:
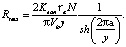 (6)
(6)
Приняв в (6) Rmax равным требуемой величине шероховатости Rz, можно определить необходимый шаг Dy расположения строк. При этом количество строк m зависит от ширины заготовки B и равно:
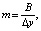 (7)
(7)
где m – количество строк; B – ширина детали, м; Dy – шаг строк, м.
На основе уравнений баланса энергии при прохождении тока электролиза через межэлектродный промежуток в течение времени tw действия импульса тока, с учетом процессов Джоулева тепловыделения и катодного газовыделения, получим систему уравнений для расчета температуры Tt и относительного объемного газонаполнения cg электролита [4]:
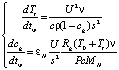 (8)
(8)
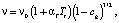 (9)
(9)
где ν, ν0 – текущая и начальная электропроводность электролита, См/м; αT – температурный коэффициент проводимости электролита, 1/K; P – давление электролита в МЭП, Па; MH – молярная масса водорода, кг/моль; εH – электрохимический эквивалент водорода, кг/Кл; ρ – плотность электролита, кг/м3; с – теплоемкость электролита, Дж/кгK; сg – относительное объемное газонаполнение; T0, Tt – начальная и текущая температура электролита, К; tw – длительность прохождения тока, с; Rg – универсальная газовая постоянная 8,314 Дж/(моль∙К); s – межэлектродный зазор, м.
Из приведенной системы уравнений (7–9) может быть определена длительность импульса tw, при которой ток через МЭП не прерывается в связи с заполнением электролита в нем газом или вскипанием. Приняв для заданных U и s в качестве максимально допустимого cg = 0,63, время протекания тока tw определим из решения системы уравнений при начальных условиях tw = 0; cg = 0; Tt = 0.
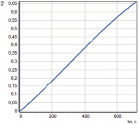
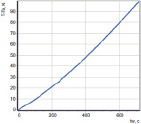
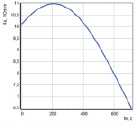
Из решения системы (7–9) следует, что проводимость ν электролита (как проводника второго рода) в начале импульса возрастает выше начальной в связи с влиянием температуры при нагреве Джоулевым теплом (рис. 2а) на проводимость электролита, а затем уменьшается в связи с возрастанием газонаполнения межэлектродного промежутка (рис. 2б) за счет выделяющегося при электролизе водорода (рис. 2в). В момент tw достижения предельного газонаполнения МЭП проводимость электролита резко снижается, и ток прерывается.
а) б) в)
Рис. 2. Изменение относительного объемного газонаполнения cg (a) и температуры Tt электролита (б) и проводимости ν электролита (в) от длительности tw протекания тока: ν0 = 10,1, См/м; P = 5·105, Па; T0 = 293, K
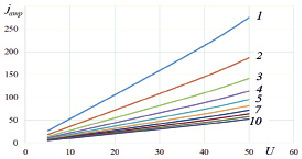
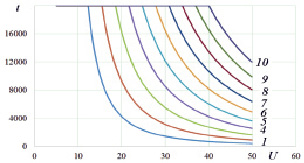
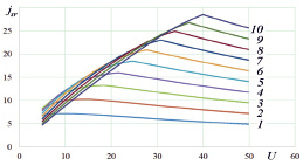
Анализ решений системы уравнений (7–9) при изменении напряжения и зазора показывает, что увеличение напряжения U и уменьшение величины межэлектродного зазора s приводят к увеличению плотности тока в импульсе ja (рис. 3а), но при этом и уменьшают его длительность tw (рис. 3б). В связи с этим средняя плотность тока jm за период следования импульсов (определяющая, в соответствии с законом Фарадея, производительность процесса) уменьшается с увеличением напряжения (рис. 3в).
а)
б)
в)
Рис. 3. Изменение выходных показателей процесса ja, jm, tw при различных значениях напряжения U, В и величины зазора s, мкм: a – изменение амплитудной плотности тока в импульсе jа, А/см2; б – изменение длительности tw прохождения тока (до достижения предельного газонаполнения cg = 0,63), мкс; в – изменение средней (за период следования импульсов) плотности тока jm, А/см2. Во всех случаях начальная проводимость электролита ν0 = 10,1, См/м; P = 5·105 , Па; T0 = 293 K; кривые 1–10 на всех графиках построены для разных величин зазоров от 50 до 550 мкм соответственно, с шагом 50 мкм
При электрохимической обработке шероховатость Rz и глубина измененного слоя H (с растравом по границам зерен) на обработанной поверхности, как правило, уменьшаются с увеличением плотности тока ja и могут быть, например, для сплавов на никелевой основе для ja плотность тока, А/см2 в диапазоне 5 ≤ ja ≤ 80 описаны следующими эмпирическими функциями для:
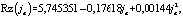 (10)
(10)
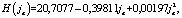 (11)
(11)
где ja – плотность тока, А/см2; Rz – средняя высота микровыступов, мкм; H – глубина измененного слоя, мкм при ja > 80, Rz = 0,7, H = 0.
Плотность тока ja в формулах (10), (11) может быть определена по формуле для точки поверхности, расположенной на оси ЭИ (x = 0, y = 0, рис. 1а):
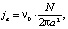
где ja – амплитудная плотность тока, А/м2; ν0 – начальная электропроводность электролита, См/м; N – интенсивность источника, Вм, a – расстояние до эквивалентного источника, м.
Однако, как было показано выше, снять весь припуск при высокой плотности тока и получить финишные значения шероховатости малопроизводительно, так как это спряжено со снижением эффективной длительности импульса и, соответственно, снижением средней плотности тока (рис. 3а, 3б, 3в). В связи с этим целесообразно разделить припуск на части (рис. 4) и удалять его за соответствующее число проходов, удаляя каждый слой металла в каждом проходе на оптимальных по суммарному времени обработки tsum режимах.
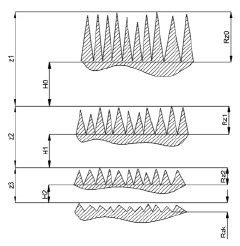
Рис. 4. Расчетная схема припусков для 3 проходов
При нескольких проходах i = 1, …, n общее время обработки tsum обработки складывается из суммы времен ti удаления каждой части припуска:
tsum = t1 + t2 +….+ tn, (12)
где
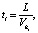 (13)
(13)
где L – длина детали.
На каждом i-м проходе ЭИ, движущегося над поверхностью с зазором si со скоростью 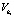 , формируется поверхность как результат наложения единичных следов, при этом снимается припуск zi и формируется определенный профиль z(y) (рис. 1) c шероховатостью Rzi и глубиной измененного слоя Hi. На каждом последующем i + 1-м проходе ЭИ сдвигался в направлении обработанной поверхности до образования с ней по оси O-Z (в точке y = 0) величины зазора si+1.
, формируется поверхность как результат наложения единичных следов, при этом снимается припуск zi и формируется определенный профиль z(y) (рис. 1) c шероховатостью Rzi и глубиной измененного слоя Hi. На каждом последующем i + 1-м проходе ЭИ сдвигался в направлении обработанной поверхности до образования с ней по оси O-Z (в точке y = 0) величины зазора si+1.
Величина минимального припуска zi, необходимого для удаления шероховатости и измененного слоя предшествующей i-1 поверхности для формирования новой i, может быть определена по формуле:
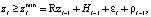 (14)
(14)
где Hi-1 – глубина измененного слоя (в случае электрохимической обработки сплавов на никелевой основе это слои с растравом по границам зерен); Rzi-1 – высота микронеровностей профиля по 10 точкам; ri-1 – сумма отклонений для элементарной поверхности обрабатываемой заготовки на предшествующем переходе; ei – погрешность базирования заготовки на выполняемом переходе; индексы i и i-1 обозначают соответственно текущую и предшествующую обработку.
Поскольку при электрохимической обработке физический износ электрода-инструмента (катода) практически отсутствует, обработка будет вестись одним ЭИ с неизменной установкой в приспособлении при последовательном изменением режимов на проходах, величины ρ, ε принимаются равными нулю и учитываются на завершающей операции технологического процесса обработки детали.
Суммарное время tsum удаления общего припуска при его разбиении на n частей
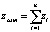
может быть определено как функция 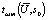 по формуле:
по формуле:
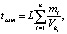 (15)
(15)
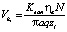 , (16)
, (16)
где 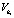 – скорость подачи ЭИ на i-м переходе; mi – число строк (определяется из выражения (6));
– скорость подачи ЭИ на i-м переходе; mi – число строк (определяется из выражения (6));
Rzi-1, Rzi – высота микронеровностей профиля для переходов i-1 и i.
Постановка задачи оптимизация
Дана заготовка с исходной поверхностью, эквидистантной к поверхности детали, имеющая начальную шероховатость Rz0, глубину измененного слоя H, погрешность Dz0. Требуется получить деталь с шероховатостью не более Rzn с измененным поверхностным слоем толщиной не более Hn и погрешностью не более Dzn. Деталь обрабатывается за n проходов, при этом на каждом проходе снимается часть zi общего припуска zsum.
Задача оптимизации может быть сформулирована следующим образом: определить такие параметры (Ui, si) режима обработки на каждой части zi припуска zsum при заданном его разбиении на n частей, при которых суммарное время обработки, равное сумме времен удаления каждой части припуска 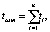 будет минимально: tsum = toptimum, т.е.
будет минимально: tsum = toptimum, т.е.
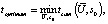
при условиях:
Rzk ≤ Rzmax, Rzi < Rzi-1,
Hk ≤ Hmax, Hi < Hi-1,
Dzi ≤ Dzmax, Dzi < Dzi-1,
и ограничениях на диапазоны изменения параметров режима (при разбиении диапазона на k частей):
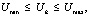
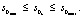
Для расчета Rzi и Ti могут быть использованы эмпирические зависимости (10, 11).
Величина погрешности на текущем проходе Dzi может быть определена на основе следующих соображений (рис. 5):
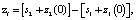 (17)
(17)
где s1, s2 – соответственно зазоры между ЭИ и наиболее выступающей и наиболее вогнутой частями макрорельефа обрабатываемой поверхности; z1(0), z2(0) в соответствии с (2) – глубины следа ЭИ в точке y = 0 для зазоров, где s1, s2; s2 = s1 + Dzi–1 соответственно.
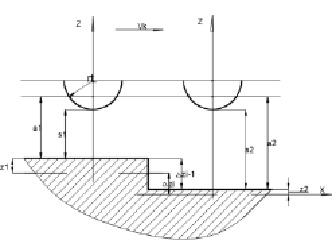
Рис. 5. Схема формирования погрешности
Подставив из (2) в выражение (17) формулу для z(y) при y = 0 для зазоров s1, s2, после преобразований получим:
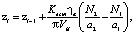
где Dzi, Dzi–1 – погрешность формы соответственно на данном и предшествующих проходах; N1, N2 – интенсивность источника (1а) для наименьшего и наибольшего зазоров соответственно, s1i-1, s2i-1; a1, a2 – расстояние до эквивалентного источника (1в), соответственно для наименьшего и наибольшего зазоров s1, s2.
Пример расчета оптимальных режимов при разбиении припуска на три (n = 3) части приведен на рис. 6. Расчет производился по представленной выше математической модели в следующих диапазонах входных параметров Uk, 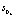 , k = 1, …, m,: (m = 10)
, k = 1, …, m,: (m = 10)
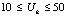 , с шагом 10 В;
, с шагом 10 В;
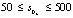 , с шагом 50 мкм.
, с шагом 50 мкм.
а) б) в)
г) д) е)
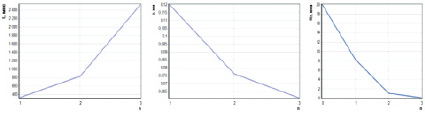
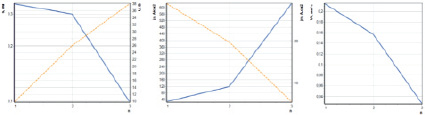
Рис. 6. Пример результатов расчета оптимальных режимов при трех (i = 1..n) проходах удаления суммарного припуска zsum: а – время t удаления каждой i-й части припуска; б – величины припусков, снимаемых на каждом i-м проходе zi ; в – шероховатость обработанной поверхности, достигаемой на каждом i-м проходе Rzi; г – величины межэлектродных зазоров si (сплошная кривая) и напряжений Ui (пунктирная кривая) на каждом проходе; д – амплитудная ja (сплошная кривая) и средняя jm за период (пунктирная кривая) плотности токов; е – скорость подачи ЭИ на каждом проходе Vki
На рис. 6 показано изменение оптимальных параметров процесса при переходе от первого прохода к последнему.
Показано, в частности, что к последнему происходят увеличение напряжения U и уменьшение межэлектродного зазора s (рис. 6г), что вызвано требованиями снижения шероховатости Rz, измененного слоя H и погрешности Dz, соответственно изменению отношения U/s по уравнениям (7)–(9) увеличивается амплитудный ja и уменьшается средний ток 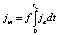 (рис. 6д). При этом, несмотря на уменьшение припуска z (рис. 6б), уменьшается скорость подачи Vk (рис. 6е) и увеличивается время обработки t (рис. 6а).
(рис. 6д). При этом, несмотря на уменьшение припуска z (рис. 6б), уменьшается скорость подачи Vk (рис. 6е) и увеличивается время обработки t (рис. 6а).
Величины снимаемых припусков zi на каждом проходе могут быть использованы для определения суммарного припуска zsum при проектировании операционной заготовки.
Выводы
Разработана математическая модель последовательно-строчной многопроходной электрохимической обработки стержневым ЭИ с полусферическим рабочим торцом. Использование этой модели позволило поставить и решить задачу оптимизации параметров режима многопроходной обработки для достижения минимального времени выполнения операции.
Показано, что требование уменьшения шероховатости поверхности требует увеличения плотности тока, вместе с тем средний ток и скорость подачи соответственно увеличиваются, так как за счет процессов нагрева и вскипания электролита уменьшается эффективная длительность tw действия тока.
Показано, что разбиение припуска на n частей позволяет снизить суммарное время обработки, так как дает возможность осуществить обработку первых слоев с наибольшей производительностью. Однако при увеличении количества проходов более n > 3 суммарное время существенно не изменяется.
Приведен пример расчета оптимальных параметров режима и припусков в практической области изменения параметров.
Работа проведена при финансовой поддержи по гранту РФФИ (код проекта 17-07-00356).
Библиографическая ссылка
Зайцев А.Н., Житников В.П. ОПТИМИЗАЦИЯ РЕЖИМА ПОСЛЕДОВАТЕЛЬНО-СТРОЧНОЙ ЭЛЕКТРОХИМИЧЕСКОЙ ОБРАБОТКИ СТЕРЖНЕВЫМ ЭЛЕКТРОД-ИНСТРУМЕНТОМ // Современные наукоемкие технологии. 2021. № 4. С. 42-50;URL: https://top-technologies.ru/ru/article/view?id=38613 (дата обращения: 02.01.2026).
DOI: https://doi.org/10.17513/snt.38613



