На сегодняшний день трудно представить развитие отраслей регионов без тщательного мониторинга и многоуровневого анализа данных, в том числе получаемых методами дистанционного зондирования Земли (ДЗЗ). Данные зондирования могут быть эффективно применены в различных областях машиностроения, обороны и пр. [1–4]. С помощью средств ДЗЗ можно оперативно реагировать и даже предупреждать масштабные экологические катастрофы, такие как недавний разлив нефтепродуктов в Норильске [5], что тоже положительно сказывается на благосостоянии региона. В работе [6] показаны перспективы использования современных неогеографических технологий, в том числе на основе методов ДЗЗ и цифровых моделей регионов. В исследовании [7] были обработаны и проанализированы показатели ночной освещенности наблюдаемых территорий. Оказалось, что данные ночной освещенности регионов имеют высокую корреляцию с уровнем их социально-экономического развития. Чем выше региональный валовый продукт, тем более высокий уровень ночной освещенности городов.
Таким образом, задача обработки данных ДЗЗ в рамках социо-эколого-экономического мониторинга регионов является на сегодняшний день крайне актуальной. Не менее важной задачей в рамках построения систем мониторинга средствами беспилотных летательных аппаратов (БПЛА) является разработка новых методов обработки изображений на борту БПЛА, учитывающих ограничения бортовой вычислительной системы. Такой подход позволяет оперативно выявлять события в регионах там, где невозможно использовать каналы передачи данных к высокопроизводительным вычислительным комплексам обработки.
Исследование посвящено созданию комплексного подхода к анализу социо-эколого-экономического состояния регионов. Разработанный метод опирается на данные, в том числе от средств дистанционного зондирования Земли. Достигается снижение нагрузки на бортовую аппаратуру БПЛА при решении задачи сегментации зон на изображениях. Решение поставленных задач ориентировано на оценку актуального состояния изучаемых регионов.
Материалы и методы исследования
1. Методы анализа состояния регионов
Анализ состояния наблюдаемых регионов позволяет оперативно выявлять изменения ситуации, предотвращая развитие неблагоприятных факторов. Для контроля состояния регионов предлагается использовать следующие методы:
– математические модели развития региона [2] для оценки и прогнозирования состояния;
– метод инвариантных моментов для распознавания ригидных объектов и зон с четкими геометрическими границами [8];
– сверточные нейронные сети для выявления зон и объектов интереса.
Актуальный пример системы анализа состояния региона с помощью данных дистанционного зондирования можно обнаружить в работе [9]. Предлагается рабочее место как автоматизированный инструмент интеллектуальной системы мониторинга территорий с функциями высокоскоростной обработки данных и поддержки лиц, принимающих решения.
В качестве примера рассмотрим математическую модель засева подготовленных аграрных площадей различными культурами. Рассмотрим задачу линейного программирования.
Пусть даны три типа культур, которые засеиваются на трех площадях: x1, x2 и x3, имеющих известную выходную прибыль за единицу площади засева: a1, a2 и a3, соответственно. Целевая функция прибыли, которую мы максимизируем:
,
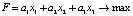при ограничениях
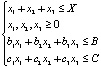, (1)
где X – общая доступная площадь для засева площадей xi (i = 1, 2, 3) под различные культуры; ai (i = 1, 2, 3) – известная выходная прибыль с трех культур; bi – трудовые ресурсы на каждый тип культур за единицу площади; B – общий доступный объем трудовых ресурсов; ci – финансовые затраты на засев и сопровождение роста культур за единицу площади; C – общий доступный объем финансов.
Данную задачу можно решить, например, не требовательным к временным и вычислительным ресурсам симплекс-методом. В систему (1) могут быть включены ограничения на производимые в рабочем процессе вредные вещества, в том числе негативно влияющие на почву, либо риски потерь урожая. Понятно, что с течением времени площади засева могут меняться как от природных явлений, так и вследствие деятельности человека. Лесные пожары, ураганы и прочие негативные факторы накладывают дополнительные ограничения. Можно уточнять и добавлять в систему (1) новые условия, совершенствуя модель в целях повышения благосостояния региона [3].
Для оперативного мониторинга зон, в частности для задачи, рассмотренной выше, предлагается использовать методы инвариантных моментов, которые на сегодняшний день широко используются в различных областях. Инварианты позволяют выполнять распознавание объектов независимо от их положения на наблюдаемой поверхности. Контурный анализ позволяет выполнять распознавание в условиях естественного колебания освещенности, так как извлекаемые контуры устойчивы к таким флуктуациям [8]. Перечисленные методы можно использовать для вычисления площадей и выявления изменений в границах лесных и аграрных зон. При этом мы выигрываем на том, что фактически не нужно организовывать обучение, алгоритмы вычисления дескрипторов имеют малую вычислительную сложность, само количество инвариантов незначительное. Отметим, что в условиях сильной зашумленности снимков, нечетких границ или наличия сложных текстур наблюдаемой поверхности данный метод уступает интеллектуальным методам обработки изображений на основе искусственных нейронных сетей (ИНС).
Постоянно растущие объемы пополняемых данных ДЗЗ существенно повысили требования к скорости и качеству передачи и обработки информации. В настоящее время все активнее применяют сверточные нейронные сети (СНС) и технологии высокопроизводительных вычислений. Современные ИНС могут не только классифицировать целевые объекты, но и указывать их позиции на снимке ДЗЗ. Так, в работе [9] описаны исследования по использованию модифицированной СНС типа Darknet в задаче обнаружения и распознавания целевых объектов. При этом для ускорения вычислений задействованы графические процессорные устройства как при обучении нейронных сетей, так и при их последующем использовании. Проведенные исследования показали высокую скорость обработки снимка ДЗЗ (от 2 до 6 сек., в зависимости от разрешения) при достаточно высокой точности и полноте распознавания, F1 – мера различных тестов составила от 0.85 до 0.91.
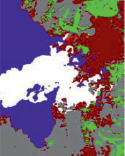
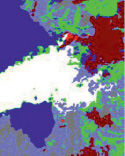
Отдельно можно упомянуть метод «спектрографической закраски» (рис.), который хорошо себя зарекомендовал, в том числе в качестве инструмента классификации зон поверхности Земли. В основе метода сканирующее окно, захватывающее спектральные и статистические информативные параметры обрабатываемых изображений.
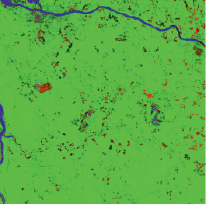
Пример «спектрографической закраски» различных зон региона
Данная задача по сути является задачей классификации различных зон на фотоснимке, сделанном с БПЛА, ее решение помогает с оперативным обнаружением лесных пожаров, разливов нефтепродуктов, вырубок леса, с засевом и уборкой сельскохозяйственных зон и т.д.
2. Метод закраски зон интереса с учетом ограничений бортовой вычислительной платформы
Для решения задачи «раскраски» зон интереса предлагается использовать модифицированную метрику Евклида-Махаланобиса [10]. Использование метрик на базе метрики Махаланобиса сопряжено в общем случае со значительными временными затратами. Ясно, что в случае с потоковой обработкой снимков столь значительные временные затраты в бортовых системах с ограниченными вычислительными ресурсами неприемлемы.
Для значительного снижения вычислительной нагрузки (и, как следствие, ускорения вычислений) с малой погрешностью классификации точек изображений предлагается модифицировать формулу измерения расстояния между классами. Данный подход и результаты экспериментов рассмотрим ниже.
В метрике Евклида-Махаланобиса расстояние между классами X1 и X2 определяется по следующей формуле: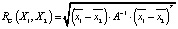 
, в которо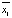й 
и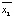 
– математические ожидания текстурных признаков в классах X1 и X2, матрица A–1 – обратная матрица произведения: 
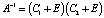, C1 и C2 – ковариационные матрицы для классов X1 и X2 соответственно. Для вычисления дистанции от класса Y до точки p применяется формула 
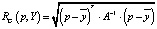, в которой используется матрица 
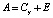. Матрица ковариаций Cy соответствующего класса Y может быть вычислена по формуле
,
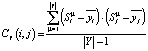в которой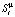 
– i-й признак μ-й текстуры из класса Y.
Для обработки мультиспектрального изображения с числом спектров k задается размер сканирующего окна – ширина и высота, xDimension и yDimension соответственно. Для полутоновых кадров k = 1, для трехканальных изображений k = 3, при этом поддержана обработка данных, представленных в различных цветовых пространствах (RGB, HSV). Выбранные параметры определяют ширину и высоту матрицы A – ее высота и ширина равны соответственно k∙xDimension∙yDimension. Обозначим указанную величину как dim.
Для значительного снижения вычислительной нагрузки с малой погрешностью классификации точек изображений предлагается следующая формула, в которой вместо всей матрицы A–1 используется лишь ее главная диагональ:
.
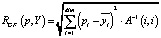Перед экспериментальной частью исследований была произведена грубая оценка сложности вычислений метрики Евклида-Махаланобиса и предложенной нами упрощенной метрики. Используем скользящее окно k×k пикселей и три канала цвета изображения. Пренебрегая операциями сложения, мы оцениваем возможное ускорение вычислений Q как
.
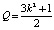Таким образом, при размере скользящего окна 15х15 пикселей и трех каналов изображения, расчетный выигрыш по времени вычислений составляет 338 раз по сравнению со стандартным методом расчета метрики Евклида-Махаланобиса.
Результаты исследования и их обсуждение
Далее представлены результаты проведенных экспериментов с предложенным методом «закраски» зон интереса.
Эксперимент 1. Проводилось тестирование предложенной модифицированной метрики на задаче выделения зон интереса. Испытание произведено с использованием одного ядра процессора Intel Core i5-4670. Тест состоял из шести изображений размерами (в пикселях): 1428x847, 1371x817, 1440x822, 1248x896, 1440x867 и 1440x861.
В обучающей выборке имелось 16 классов зон интереса. По изображениям при закраске перемещается окно 15x15 пикселей, в каждой позиции учитываются три цветовые составляющие (цветовая модель HSV).
По серии проведенных экспериментов (5 раз) получено среднее значение времени работы алгоритма:
– 28335 секунд без модификации;
– 80 секунд на модифицированной метрике.
Таким образом, экспериментально получено ускорение в 352 раза. Кроме того, можно отметить, что на оригинальной метрике Евклида-Махаланобиса алгоритм закрасил большой объем «воды» там, где ее нет (ложноположительный результат). В табл. 1 показаны результаты тематической «закраски».
Таблица 1
Результаты экспериментов по «закраске» зон интереса
|
Исходное изображение |
Оригинальная метрика |
Модифицированная метрика |
|
|
|
|
|
Продолжение табл. 1 |
||
|
Исходное изображение |
Оригинальная метрика |
Модифицированная метрика |
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 1 |
||
|
Исходное изображение |
Оригинальная метрика |
Модифицированная метрика |
|
|
|
|
|
|
|
|
Ввиду отсутствия эталонной разметки зон интереса на снимках ДЗЗ, не представляется возможным строго оценить влияние предложенной упрощенной метрики Евклида-Махаланобиса на точность раскраски, однако визуально можно отметить улучшение качества раскраски зон.
Эксперимент 2. В табл. 2 представлен пример результатов обработки изображений с лесными пожарами методом «закраски» с обычной метрикой и предложенной модифицированной.
Таблица 2
Результаты экспериментов с «закраской» снимков ДЗЗ с пожарами
|
Исходное изображение |
Оригинальная метрика |
Модифицированная метрика |
|
|
|
|
Результаты обработки:
– метрика Евклида-Махаланобиса: 3211 сек.;
– упрощенная метрика Евклида-Махаланобиса: 8 сек.;
– полученное ускорение: в 393 раза.
Эксперимент 3. Для имитации вычислений на борту использовался микропроцессор с архитектурой ARM.
В задаче «закраски» использовалось одно ядро ARMv7 rev.1, которое по проведенным тестам производительности медленнее одного ядра Intel Core i5-4670 в 4 раза. Результаты тестов на шести снимках ДЗЗ:
– время работы на ARM оригинального алгоритма: 133068 сек.;
– время работы на ARM модифицированного алгоритма: 328 сек.;
полученное ускорение: 405 раз.
Заключение
Использование данных ДЗЗ дополнительно к стандартным методам анализа состояния региона позволит уточнить модели развития и оперативно реагировать на изменяющиеся условия, что повышает общий уровень экономического развития в сельском хозяйстве и других отраслях наблюдаемого региона. При реализации обработки видеокадров на бортовом вычислительном комплексе БПЛА предпочтение следует отдать относительно простым методам, позволяющим выделять регионы, связанные с областями интереса пользователя, включая поиск зон чрезвычайных ситуаций методами тематической «закраски» с применением упрощенной обобщенной метрики, что позволяет значительно ускорить процесс обработки.
Работа выполнена при финансовой поддержке РФФИ (проекты № 18-29-03011-мк, № 20-07-00022-а).
Библиографическая ссылка
Абрамов Н.С., Фраленко В.П. ОЦЕНКА ЭКОНОМИЧЕСКОГО РАЗВИТИЯ РЕГИОНОВ СРЕДСТВАМИ ДИСТАНЦИОННОГО ЗОНДИРОВАНИЯ ЗЕМЛИ БЕСПИЛОТНЫМИ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ // Современные наукоемкие технологии. – 2021. – № 3. – С. 9-15;URL: https://top-technologies.ru/ru/article/view?id=38523 (дата обращения: 18.04.2024).