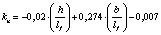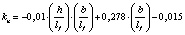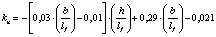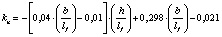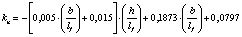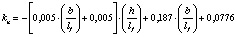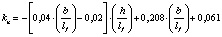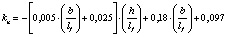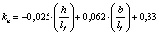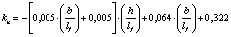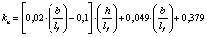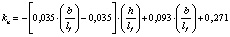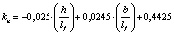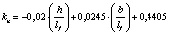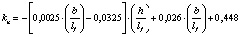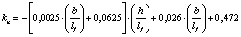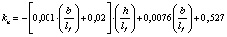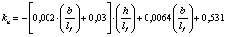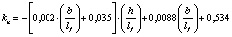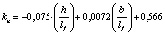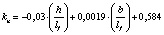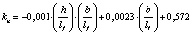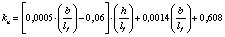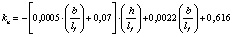В нашей стране к настоящему времени разработан Свод правил (СП), устанавливающий требования к проектированию бетонных и железобетонных конструкций [1]. Для многих расчетов [1] не дает алгоритмов вычислений, а только формулирует требования, которым должны удовлетворять результаты.
При современном развитии вычислительной техники и программного обеспечения расчеты железобетонных конструкций в подавляющем большинстве случаев проводят на ЭВМ. Используются как программы массового применения, так и разработанные для отдельных организаций. Сравнение показывает, что при одних и тех же исходных данных результаты, полученные по различным программам, могут существенно отличаться. Такое положение представляется недопустимым, поскольку нормы предполагают для каждого случая получение единственного решения. Отклонение от норм может привести как к недостаточно надежным проектным решениям, так и к удорожанию конструкций вследствие перерасхода материалов.
Для тестирования разработанных ЭВМ-программ рекомендуется использовать пособие [2], позволяющее добиться соответствия использованных авторских алгоритмов положениям [1].
Для исключения проведения сложных равновесных опытов с целью получения зависимости прогиба от действующей нагрузки на изгибаемый шлакобетонный элемент разработана математическая модель полной диаграммы деформирования шлакобетона при трехточечном изгибе, являющаяся основой для разработки ЭВМ-программ [3].
В настоящее время все больше находят применение композиты на основе дисперсно армированных бетонов [4], а шлаковый цемент и шлаковые заполнители в составе тяжелых бетонов – достаточно частое сочетание [5].
Для проектирования сталефибробетонных конструкций разработан ряд сводов правил (СП), устанавливающих требования к проектированию [6, 7] и также существуют теоретические диаграммы деформирования бетона при растяжении и сжатии для определения момента трещинообразования и разрушающего момента в изгибаемых железобетонных элементах [8].
Для многих расчетов [6, 7] не дает алгоритмов вычислений, а только формулирует требования, которым должны удовлетворять результаты.
Цель исследования: предложить математическую модель описания прочности центрально сжатого тонкостенного сталефибробетонного элемента, применение которой позволит сократить время и автоматизировать вычислительный процесс.
Известно, что дисперсное армирование осуществляется волокнами-фибрами, распределенными в объеме бетонной матрицы и наиболее эффективно в тонкостенных конструкциях (рис. 1).

Рис. 1. Распределение фибрового армирования в тонкостенном элементе
В настоящее время применяется пять способов получения стальных фибр:
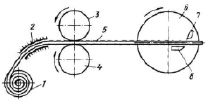
Рис. 2. Схема станка для получения фибр из стальной проволоки: 1 – бухтодержатель; 2 – направляющая; 3 – прижимной валок; 4 – приводной валок; 5 – проволока; 6 – ротор; 7 – подвижный нож; 8 – неподвижный нож
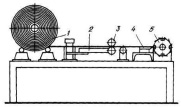
Рис. 3. Схема станка для получения фибр из листовой рулонной стали: 1 – рулон листовой стали; 2 – направляющее устройство; 3 – подающий механизм; 4 – неподвижный нож; 5 – ротор с подвижными ножами
1) из проволоки (рис. 2) с резкой и профилированием их сечения;
2) из отработанных стальных канатов с резкой последних на отрезки заданной длины, их расщеплением и очисткой от смазки;
3) из стальной полосы (рис. 3) заданной ширины с поперечной или продольной резкой специальными фрезами;
4) из стального слитка (сляба) путем фрезерования;
5) вытяжкой волокон из расплава.
Наиболее освоены и распространены в практике способы получения фибр из проволоки, отработанных канатов и тонкого стального листа (рис. 4).

Рис. 4. Виды распространенной стальной фибры: а) фибра из стального листа (ЛФ); б) фибра из проволоки (ПФ); в) фибра из стальных канатов (ТФ); г) фибра из проволоки, аналог «Драмикс» (ДФ)
Для практического применения при проектировании конструкций из сталефибробетона [5, 6] рекомендуется определять сопротивление сжатию сталефибробетона Rfb, зависящее от класса по прочности на сжатие бетона-матрицы Rb, вида и размеров фибры, коэффициента фибрового армирования по объему µfv, геометрии и размеров сечения элемента при условии учета только работы фибр, ориентированных нормально к направлению внешнего сжимающего усилия, армируемых стальной фибровой арматурой (фиброй), по формуле
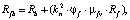 (1)
(1)
где Rf – сопротивление фибровой арматуры растяжению;
kn – коэффициент, учитывающий работу фибр в сечении, перпендикулярном направлению внешнего сжимающего усилия;
φf – коэффициент эффективности косвенного армирования фибрами.
Коэффициент, учитывающий работу фибр в сечении, перпендикулярном направлению внешнего сжимающего усилия (kn), рекомендовано определять по табл. 6.2 [6] или по табл. В.2 [7]. Значения kn в диапазоне (0,2…0,4) h/lf – (0,5…20 и более) b//lf приведены в табл. 1.
Таблица 1
Значения kn в зависимости от размеров сечения сжатого элемента при h/lf = 0,2…0,4 и b/lf = 0,5…20 и более (согласно [5] или [6])
|
Значения kn в зависимости от размеров сечения сжатого элемента при |
||||||||
|
h/lf |
b/lf |
|||||||
|
0,5 |
1 |
2 |
3 |
5 |
10 |
20 |
Более 20 |
|
|
0,2 |
0,126 |
0,263 |
0,449 |
0,511 |
0,560 |
0,597 |
0,616 |
0,636 |
|
0,4 |
0,122 |
0,259 |
0,444 |
0,506 |
0,555 |
0,591 |
0,610 |
0,629 |
|
0,6 |
0,122 |
0,257 |
0,441 |
0,502 |
0,551 |
0,589 |
0,606 |
0,624 |
|
0,8 |
0,122 |
0,253 |
0,429 |
0,494 |
0,542 |
0,578 |
0,596 |
0,614 |
|
1,0 |
0,118 |
0,247 |
0,422 |
0,480 |
0,527 |
0,563 |
0,580 |
0,597 |
В результате математической обработки данных табл. 1 получены формулы, приведенные в табл. 2, позволяющие определять с достоверностью R = 1 значения kn в расширенном (прогнозируемом) диапазоне h/lf = 0,1–0,4 и b/lf = 0,5–20,0 и более.
Размеры b и h в табл. 1 – соответственно больший и меньший размеры сечения (или его части), перпендикулярного к направлению внешнего сжимающего усилия. В составном тонкостенном сечении бетонного элемента с использованием фибрового армирования обозначение размеров приведено на рис. 5.
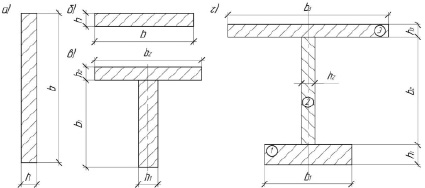
Рис. 5. Сечение тонкостенного сталефибробетонного элемента: а) и б) прямоугольное сечение, в) тавровое сечение, г) двутавровое сечение
Таблица 2
Значения kn в зависимости от размеров сечения сжатого элемента
|
Значения kn в зависимости от размеров сечения сжатого элемента |
||
|
1 |
2 |
3 |
|
b//lf |
Формула |
h/lf |
|
0,1…1,0 |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
|
1,0…2,0 |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
|
Окончание табл. 2 |
||
|
1 |
2 |
3 |
|
2,0…3,0 |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
|
3,0…5,0 |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
|
5,0…10,0 |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
|
10,0…20,0 и более |
|
0,1…0,4 |
|
|
0,4…0,6 |
|
|
|
0,6…0,8 |
|
|
|
0,8…1,0 |
|
Приведенные в табл. 2 формулы по определению значения коэффициента kn, учитывающего работу фибр в сечении, перпендикулярном направлению внешнего сжимающего усилия (при h/lf = = 0,1…0,4 и b/lf = 0,1… 2,0), явились основой для разработки программного продукта для однотипных тонкостенных конструкций [9, 10].
В данной статье приведен полный комплект формул, позволяющих автоматизировать вычислительный процесс, связанный с определением значения коэффициента (kn), в зависимости от размеров сечения сжатого элемента в расширенном диапазоне (при h/lf = 0,1…0,4 и b/lf = 2,0… 20,0 и более).
Выводы
Получены математические зависимости, с использованием которых повышается производительность расчета прочности тонкостенных сталефибробетонных элементов. Это преимущество значительно повышается при одновременном использовании различных видов фибр в разных сечениях.
Для унификации вычислительного процесса предлагается новая математическая модель зависимости коэффициента kn от длины фибры и размеров сечения:
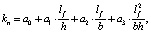 (2)
(2)
где а0, а1, а2, а3 – параметры модели, приведенные в табл. 3.
Таблица 3
Значения параметров математической модели зависимости коэффициента kn от длины фибры и размеров при h/lf = 0,2… 1,0 и b/lf = 0,5…40
|
Значения параметров в зависимости от размеров сечения сжатого элемента при b/lf |
|||||||
|
0,5–1 |
1–2 |
2 –3 |
3–5 |
5–10 |
10–20 |
20–40 |
|
|
Параметры |
при h/lf = 0,2… 0,4 |
||||||
|
а0 |
0,392 |
0,623 |
0,625 |
0,624 |
0,620 |
0,623 |
0,64 |
|
а1 |
0,0016 |
0,025 |
0,002 |
0,002 |
0,0028 |
0,0024 |
0,0032 |
|
а2 |
-0,137 |
-0,3676 |
-0,371 |
-0,368 |
-0,35 |
-0,38 |
-0,72 |
|
а3 |
0 |
-0,0009 |
0 |
0 |
-0,004 |
0 |
-0,016 |
|
Параметры |
при h/lf = 0,4… 0,6 |
||||||
|
а0 |
0,384 |
0,6179 |
0,5781 |
0,6167 |
0,6269 |
0,6109 |
0,630 |
|
а1 |
0,0048 |
0,0042 |
0,0274 |
0,0048 |
0 |
0,0072 |
0,0072 |
|
а2 |
-0,131 |
-0,3649 |
-0,2524 |
-0,3684 |
-0,4195 |
-0,2589 |
-0,6404 |
|
а3 |
-0,0024 |
-0,0019 |
-0,068 |
0 |
0,0238 |
-0,0484 |
-0,0479 |
|
Параметры |
при h/lf = 0,6… 0,8 |
||||||
|
а0 |
0,360 |
0,5450 |
0,6241 |
0,5824 |
0,5751 |
0,5870 |
0,602 |
|
а1 |
0,0192 |
0,048 |
0 |
0,0253 |
0,0312 |
0,0216 |
0,0240 |
|
а2 |
-0,119 |
-0,304 |
-0,4622 |
-0,3371 |
-0,3003 |
-0,4196 |
-0,7209 |
|
а3 |
-0,0096 |
-0,0384 |
0,0578 |
-0,0183 |
-0,0478 |
0,0477 |
0,0007 |
|
Параметры |
при h/lf = 0,8… 1,0 |
||||||
|
а0 |
0,344 |
0,565 |
0,484 |
0,5430 |
0,539 |
0,529 |
0,542 |
|
а1 |
0,032 |
0,032 |
0,112 |
0,0545 |
0,06 |
0,068 |
0,072 |
|
а2 |
-0,121 |
-0,342 |
-0,18 |
-0,357 |
-0,36 |
-0,26 |
-0,52 |
|
а3 |
-0,008 |
-0,008 |
-0,168 |
0,0046 |
0 |
-0,08 |
-0,16 |
Таким образом, предложены зависимости и математические модели, позволяющие автоматизировать вычислительный процесс, связанный с определением сопротивления сжатию Rfb, необходимого для проектирования тонкостенных составных конструктивных элементов из сталефибробетона.
Библиографическая ссылка
Черноусов Н.Н., Стурова В.А., Чурсин Е.В., Ливенцева А.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЧНОСТИ ЦЕНТРАЛЬНО СЖАТОГО ТОНКОСТЕННОГО СТАЛЕФИБРОБЕТОННОГО ЭЛЕМЕНТА // Современные наукоемкие технологии. 2021. № 2. С. 81-87;URL: https://top-technologies.ru/ru/article/view?id=38498 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.38498