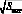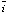В процессе теоретических исследований определился ряд связей между элементами системы, характер которых может быть выяснен только экспериментальным путем. Специфика этих связей определяет методику эксперимента, результатом которого являются зависимости:
- объекты строительных работ – зависят от характера рельефа местности, типа продольного профиля и ширины земляного полотна;
- скорость автомобильного потока – зависит от геометрических элементов дороги, интенсивности и состава движения.
В связи с поставленными целями экспериментальные работы проводились по двум направлениям:
- первое направление основывалось на анализе и статистической обработке материалов проектов дорог.
- второе направление – экспериментальные исследования, касающиеся определения зависимости скорости движения автомобильного потока, проводились на дорогах республики Коми.
Цель работы заключается в исследовании результатов наблюдений рельефа местности и статистических характеристик продольного профиля проектных материалов для технико-экономического обоснования.
Особенность методики исследования скоростей движения лесовозного подвижного состава заключалась в измерении скоростей движущихся автомобилей в зависимости от ширины проезжей части и типа продольного профиля дороги. В связи со сложностью выбора соответствующих экспериментальных участков дорог, экспериментальные исследования производились раздельно. В соответствии с двумя видами измерений разрабатывалась регистрирующая аппаратура.
Обработка результатов наблюдений скоростей производилась с привлечением аппарата корреляционно-регрессионного анализа, и в результате получены уравнения связи скорости автомобильного потока в зависимости от интенсивности, состава потока, распределения продольных уклонов и ширины проезжей части дорог.
Для охвата исследованиями возможно большего разнообразия форм рельефа выбор проектов для обработки производился целенаправленно, с контролем объема и характера совокупности.
После деления продольных профилей на участки с однородными топографическими условиями в специальные таблицы выписывались отметки земли через 200 м. В результате расчета интеллектуально-информационной системой получены кривые пересеченной местности и параметры рельефа «У» и «m».
Расчет кривых пересечённой местности для большего количества проектов дорог, составленных для самых различных типов рельефа местности, позволил более глубоко вникнуть в физический смысл кривых и классифицировать рельеф с учетом параметров «У» и «m». Придерживаясь принятой классификации рельефа по пяти группам, можно получить пределы изменения параметров для этих групп (табл. 1).
Таблица 1
Пределы изменения параметров
|
Параметр |
Группы рельефа |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
У |
098–4,94 |
1,82–14,03 |
3,56–33,82 |
13,75–32,19 |
32,00–63,31 |
|
m |
633–28848 |
501–6009 |
606–10549 |
1228–5514 |
996–22285 |
На рис. 1 представлены кривые пересечённости, представляющие группы рельефа. Как выяснилось, за основу классификации может быть принят один из параметров, при этом второй будет изменяться произвольно, в зависимости от характера местности. В данном случае основным принят параметр «У», так как общепринятая классификация по пересечённой местности рельефа предусматривает в основном различие групп по перепаду высот [1–3].
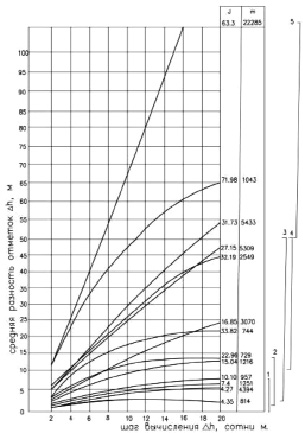
Рис. 1. Классификация рельефа местности по типу кривых пересеченности
Результаты проведенных исследований и сравнение рельефа по существующему методу и по методу кривых пересеченной местности показывают, насколько неточна и субъективна визуальная оценка сложности рельефа. Для целей дорожного проектирования необходима математическая оценка рельефа в каждом конкретном случае.
Одновременно с выборкой отметок земли производилась систематизация проектных уклонов продольного профиля.
Как уже упоминалось ранее, оценка трудности продольного профиля участка лесовозной автомобильной дороги с точки зрения затрат на перевозки может быть оценена по ее структуре. Также должна приниматься во внимание и протяженность участков с различными углами [4–6]. Однако наиболее существенное влияние на скорость автомобиля на определённом поперечнике оказывает значение продольного уклона.
Для определения частотностей уклонов каждого участка выполнены вычисления средних значений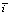 
и среднеквадратические отклонения σi по следующим формулам:
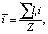(1)
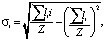(2)
где li – протяженность участка с уклоном i;
z – общая длина оцениваемого профиля.
В результате анализа выборок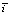 
и σi для экспериментальных участков выяснилась тесная связь между ними (рис. 2). Путем аппроксимации с применением современных математических пакетов по экспериментальным данным получена следующая зависимость:
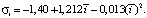(3)
Наличие связи (3) объясняется тем, что кривые распределения уклонов ограничены слева нулевым значением, а увеличение среднего значения уклонов сопровождается увеличением отклонений.
Вид распределения проектных продольных уклонов в значительной мере определяется типом рельефа местности, однако техническая категория ограничивает частоты предельных уклонов пересечённой местности.
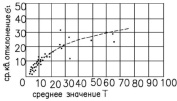
Рис. 2. Поле корреляции значений T и σi
Влияние рельефа на распределение продольных уклонов позволило классифицировать распределение в группы, соответствующие типам рельефа. На рис. 3 и 4 приводятся характерные для каждой группы рельефа распределения уклонов продольных профилей. Повышение группы рельефа сопровождается увеличением статистического среднего значения уклона и среднеквадратического отклонения. Для последующих вычислений и анализа распределений уклонов необходимо брать выравнивающую теоретическую кривую, описывающую эмпирические полигоны.
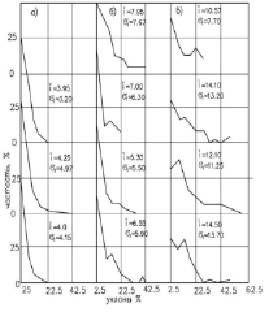
Рис. 3. Полигоны распределений проектных продольных уклонов: а) для рельефа 1 группы; б) для рельефа 2 группы; в) для рельефа 3 группы
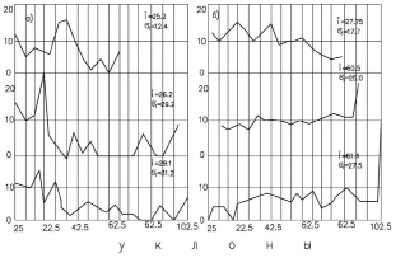
Рис. 4. Полигоны распределений проектных продольных уклонов: а) для рельефа 4 группы; б) для рельефа 5 группы
В качестве гипотезы принято гамма-распределение, по форме наиболее подходящее для описания данных эмпирических рядов, относящихся к группам рельефа.
Плотность гамма-распределения выражается следующим образом:
f(x, m, λ) =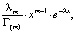 
(4)
где Г(m) – гамма-функция;
λ и m – параметры распределения.
Математическое ожидание гамма- распределения:
М[x] =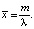 
(5)
Среднеквадратическое отклонение:
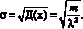(6)
Для проверки статистической гипотезы были выбраны 22 типичных полигона.
Расчет теоретических частот гамма-распределения производился с применением современных математических пакетов.
В качестве критерия согласия принимается критерий Χ2, как наиболее мощный по сравнению с другими непараметрическими критериями. Применение Χ2 оправдывается и тем обстоятельством, что выборка, подлежащая оценке, достаточно велика (n > 100). Критерий Χ2 вычисляли по формуле 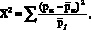[7]:
(7)
где р – наблюденные частоты;
– выравнивающие частоты.
Критерий Χ2 выражает степень расхождения экспериментального и теоретического распределения. Производилась оценка вероятности попадания вычисленной величины Χ2 в критическую зону Χ2-распределения. На рис. 5 представлены отдельные распределения из показавших наилучшее соответствие гамма-распределений.
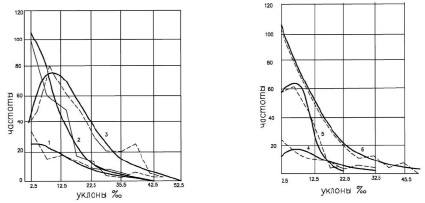
Рис. 5. Выравнивание полигонов распределения продольных уклонов
Подбор теоретической кривой, выравнивающей распределение продольных уклонов, является сложной задачей, и для её решения, возможно, потребуется исследование значительно большего количество экспериментальных выборок, но подтверждение гипотезы о гамма-распределении дает основание полагать, что в большинстве случаев продольные уклоны распределены по закону близкому к этой теоретической кривой. Следующим этапом исследования оценки рельефа и статистических характеристик продольного профиля является определение характера их совместного влияния на объем земляных работ.
По продольным профилям экспериментальных участков выполнены вычисления объема земляных работ на 1 км. Затем составлена корреляционная таблица, в которую вошли объемы земляных работ, характеристики рельефа «У» и «m» и статистические характеристики продольного профиля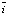 
и σi. Объем выборки n = 28 [8–10].
Важнейшим вопросом многофакторного корреляционного анализа является вопрос о форме связи зависимой переменной от независимых факторов. Графическое исследование показало, что можно предположить две гипотезы о форме связи:
У =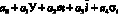 
(8)
и
У = 
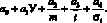(9)
Коэффициенты регрессии и остаточные дисперсии по двум гипотезам были вычислены при помощи стандартных компьютерных программ (табл. 2).
Таблица 2
Коэффициенты регрессии и остаточные дисперсии по двум гипотезам
|
Гипотеза |
Коэффициенты регрессии |
|
||||
|
а0 |
а1 |
а2 |
а3 |
а4 |
||
|
1 |
17,95 |
0,808 |
0,000779 |
-0,998 |
0,199 |
6,12 |
|
2 |
8,07 |
0,21 |
14288,0 |
39,88 |
-6,77 |
6,80 |
Нами была принята первая гипотеза, поскольку линейное уравнение связи описывает выборку с меньшей ошибкой. Следовательно, уравнение множественной корреляционной связи покилометровых дополнительных объемов земляных работ с характеристиками рельефа и продольного профиля примет вид
Q = 17,95 + 0,808У – 0,000779m +
+ 0,199σi – 0,998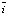
. (10)
Уравнение (10) предполагает ширину земляного полотна 10 м. Переход к любой другой ширине производится путем простых вычислений. Область действия зависимости (10) определяется граничными значениями независимых факторов, вошедшими в выборку (табл. 3).
Таблица 3
Граничные значения независимых факторов
|
Параметр |
m |
У |
|
σi |
|
max значение |
7539 |
31,73 |
32,29 |
29,19 |
|
min значение |
817 |
1,06 |
2,57 |
0,56 |
Как видно из табл. 3, действие формулы (10) распространяется на рельеф по характеристикам «У»,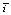 
и σi.
Таким образом, в результате статистического анализа материалов проектов лесовозных автомобильных дорог произведена отработка методики оценки рельефа местности, получены статистические характеристики проектного продольного профиля дороги и уравнение множественной корреляционной связи объема дополнительных земляных работ. Уравнение (10) позволит учесть влияние продольного профиля и рельефа местности на размер капитальных затрат при строительстве лесовозных автомобильной дороги с заданным техническим состоянием.
Выводы
Выполненные экспериментальные исследования и результаты обработки полученной информации позволяют сделать следующие выводы:
1. Оценка рельефа местности при помощи кривых позволяет получить необходимые данные о рельефе для использования в технико-экономических расчетах. На основе параметров характеристики рельефа «У» и «m» возможна классификация типов рельефа по пересеченности.
2. Исследование распределений проектных продольных уклонов лесовозных автомобильных дорог различных технических категорий, изменение характера распределения в зависимости от сложности рельефа местности даёт основание принять в качестве характеристики продольного профиля средние значения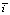 
и средние квадратические отклонения уклонов σi.
Статистический анализ характерных распределений продольных уклонов показал, что продольные уклоны дорог запроектированных в 1–3 в группах рельефа, подчиняются закону гамма-распределения. Подбор выравнивающей кривой распределения продольных уклонов позволяет глубже изучить характер влияния продольного профиля дороги на элементы целевой функции.
3. На объемы земляных работ, прежде всего, оказывают влияние тип рельефа местности и характер продольного профиля. В результате совместного анализа параметров рельефа «У» и «m» и статистических характеристик продольного профиля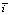 
и σi получены множественные корреляционные уравнения, характеризующие объем земляных работ в зависимости от указанных параметров. Уравнение носит линейный характер и позволяет приближённо определять оплачиваемый объем работ на 1 км продольного профиля при известных «У», «m», 
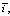и σi.
Библиографическая ссылка
Саблин С.Ю., Скрыпников А.В., Козлов В.Г., Никитин В.В., Тихомиров П.В. ТЕХНИКО-ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПРОДОЛЬНОГО ПРОФИЛЯ ЛЕСОВОЗНЫХ АВТОМОБИЛЬНЫХ ДОРОГ НА ОСНОВЕ ПРОЕКТНЫХ МАТЕРИАЛОВ // Современные наукоемкие технологии. – 2021. – № 2. – С. 63-69;URL: https://top-technologies.ru/ru/article/view?id=38495 (дата обращения: 21.11.2024).