На текущем этапе развития нефтегазовой геологии при изучении свойств геологических объектов важная роль отводится методам математического моделирования.
В широко применяемом традиционном подходе для построения и изучения петрофизических моделей исследуемых объектов используется набор методов математической статистики для обработки данных [1]. На подготовительной итерации на основе эмпирического набора данных строится оценка меры плотности связи между параметрами, полученная согласно законам, общим для всей зависимости. Далее, согласно требованиям выбранного метода, выявленный закон по виду уравнений связи между набором исследуемых параметров переносится на исходный геологический объект. При решении задач построения петрофизических моделей (и не только) одним из важных вопросов является следующий: какова неоднозначность (неопределенность) конечного результата прогноза, которая накапливает внутри себя неопределенность исходных параметров на каждом шаге в цепочке преобразований, и от чего она зависит. Ответ на этот вопрос служит базисом для принятия управленческих решений, позволяющих обеспечить минимизацию технико-экономических рисков, которые связаны с планированием и разработкой нефтегазовых месторождений. Неопределенности, входящие в исходные данные и в зависимости между ними, необходимо исследовать при подсчете прогнозных параметров, составляющих итоговые геологические модели. Математическая статистика не позволяет учитывать данную непременность при построении петрофизических моделей. Поэтому описанный способ часто является основной причиной неправильных геологических выводов по уровню запасов углеводородного сырья на разрабатываемых нефтегазовых месторождениях [2, 3].
Для того чтобы избавиться от вышеописанных проблем, возникающих при построении геологических моделей методами математической статистики, предлагается исследовать и развивать альтернативное направление, которое использует методы и принципы нечеткого моделирования. Используемые ранее регрессионные зависимости между исследуемыми параметрами заменяются на построенные в виде нечетких величин и нечетких отношений отображения набора исходных параметров и зависимостей между ними [4].
Материалы и методы исследования
Рассмотрим использование принципов нечеткого моделирования при прогнозе нефтегазопромысловых параметров на примере построения прогноза для параметра нефтенасыщенности по данным, полученным на основе исследования скважин.
Далее опишем последовательность действий при построении модели.
В работе приводятся результаты прогноза нефтегазопромысловых параметров при использовании принципов нечеткого моделирования по данным четырех скважин (№ 1, 10, 11 и 12) месторождения Тимано-Печорской нефтегазоносной провинции: одновременно измеренные значения пористости и проницаемости, проницаемости и остаточной водонасыщенности, полученные при анализе кернового материала, а также функциональной зависимости нефтенасыщенности от водонасыщенности (Кн = 1 – Кв) [5].
Этап 1. Подготовительный
Шаг 1. Преобразование набора исходных данных v в форму нечетких отношений между параметрами, где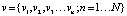 
. Преобразование реализуется путем построения функции принадлежности для каждой зависимости между парой исследуемых параметров [6].
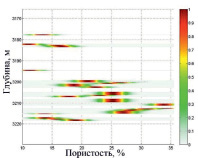
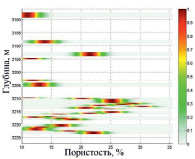
Шаг 2. Наложение выбранной сетки на множество исходных данных. В зависимости от размера сетки {M×N} определяется количество значений параметров, которые попали в одну ячейку сетки (рис. 1).
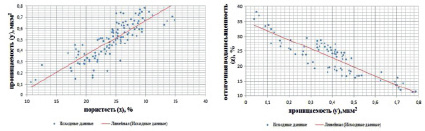
а) б)
Рис. 1. Исходные данные: а. Отношение «пористость – проницаемость»; б. Отношение «проницаемость – остаточная водонасыщенность»
После того как подсчитано количество значений в каждой ячейке сетки, устанавливается уровень погрешности и согласно невязке определяется допустимое количество источников данных:
.
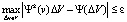Функция принадлежности μΨ(v) есть поле рассеяния источников данных, нормированное к единице Ψε(v):
.
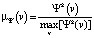Поле рассеяния имеет смысл диффузионного рассеяния в бесконечном однородном пространстве параметров точечных источников и определяется согласно следующему выражению:
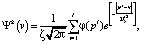
где pi – координаты сетки, где находятся источники данных, φ(pi) – значения источников [6].
Более подробно моделирование нечетких петрофизических зависимостей представлено в работе [7].
Результаты представления исходных данных в форме нечетких отношений для двух пар параметров: «пористость – проницаемость» и «проницаемость – остаточная водонасыщенность» представлены на рис. 2. Шкала справа от функции принадлежности указывает на меру доверия имеющимся данным, где красный цвет говорит о том, что этим данным можно верить больше, чем тем, которые окрашены в зеленый или желтый цвет.
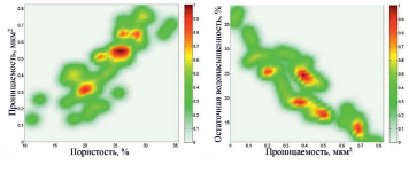
а) б)
Рис. 2. Нечеткие отношения: а. «пористость – проницаемость»; б. «проницаемость – остаточная водонасыщенность»
Этап 2. Установление взаимосвязи между исходным параметром и прогнозным
На данном этапе происходит установление взаимосвязи между исходным параметром и прогнозным. Для этого используется композиция нечетких отношений (композиция Мамани) [8, 9]:
.
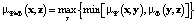Взаимосвязь между исходным и итоговым параметрами для приводимого примера рассчитывается с помощью цепочки композиций нечетких отношений.
Шаг 1. Свертка (композиция) отношения между параметрами «пористость» и «проницаемость» с отношением между параметрами «проницаемость» и «остаточная водонасыщенность».
Шаг 2. Свертка полученного отношения «пористость – проницаемость» с представленной в форме нечеткого отношения функциональной зависимостью между параметрами «остаточная водонасыщенность» и «нефтенасыщенность».
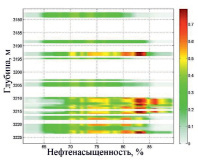
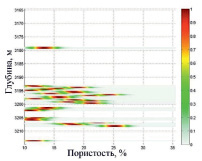
Результатом выполнения цепочки композиций является рассчитанное нечеткое отношение «пористость – нефтенасыщенность» (рис. 3).
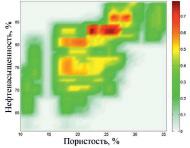
Рис. 3. Результат композиции – нечеткое отношение «пористость – нефтенасыщенность»
Этап 3. Прогноз вдоль ствола скважины
Выполняется прогноз итоговых параметров вдоль ствола скважин. Исходные данные по скважине представляются в форме нечетких величин, а затем с помощью нечеткого логического вывода (композиции Мамдани) рассчитывается функция принадлежности итогового параметра:
.
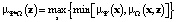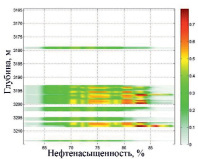
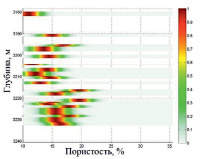
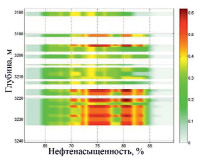
Результат прогноза параметра «нефтенасыщенность» вдоль ствола скважин представлен в табл. 1.
Таблица 1
Прогноз итогового параметра «нефтенасыщенность» вдоль ствола скважин
|
Нечеткая величина «пористость» |
Нечеткая величина «нефтенасыщенность» |
|
|
Скважина 1 |
|
|
|
Окончание табл. 1 |
||
|
Нечеткая величина «пористость» |
Нечеткая величина «нефтенасыщенность» |
|
|
Скважина 10 |
|
|
|
Скважина 11 |
|
|
|
Скважина 12 |
|
|
Этап 4. Заключительный
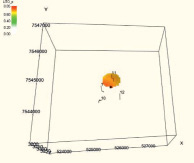
В заключение выполняются интерполяция принятых значений достоверности по скважине в межскважинное пространство и построение трехмерных геологических моделей достоверности прогнозных параметров с помощью программного продукта IRAP RMS.
Достоверность параметров при удалении от скважины убывает до критического расстояния и в пределах допустимой области рассчитывается по следующему ниже выражению:
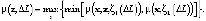
Здесь ζ(∆L) – эффективный параметр рассеяния, выступающий основным критерием при выборе математической модели функции принадлежности, ∆L – расстояние между ячейками внутри межскважинного пространства, одна из которых та, в которой рассчитывается значение, вторая – где находится скважина, в которой была определена функция принадлежности. Эффективный параметр рассеяния изменяется согласно следующему выражению:
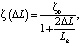
где ζ0 – используемые при расчете функции принадлежности значения эффективного параметра, которые отвечают за диффузию результатов.
Критическое расстояние определяется по выражению:
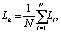
где Li – расстояние между парами скважин, N – количество скважин, задействованных в расчетах.
Результаты исследования и их обсуждение
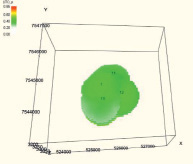
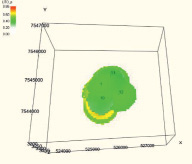
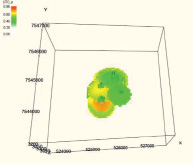
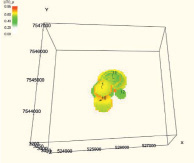
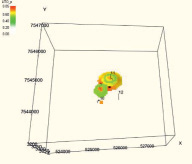
Результат интерполяции принятых значений достоверности по скважине в межскважинное пространство и построение трехмерной геологической модели распределения достоверности параметра «нефтенасыщенность» удобно представить в форме α-сечений (табл. 2). С помощью α-сечений можно определить, какая область геологической модели соответствует заданному значению достоверности.
Таблица 2
Последовательность α-сечений достоверности нефтенасыщенности с шагом 0,1
|
α = 0.1 |
α = 0.2 |
|
|
|
|
α = 0.3 |
α = 0.4 |
|
|
|
|
α = 0.5 |
α = 0.6 |
|
|
|
Построенная трехмерная геологическая модель распределения достоверности нефтенасыщенности в форме α-сечений позволяет проследить неоднородность частей модели информационной обеспеченности. С учетом высокого уровня дифференции по результатам исследования можно сделать заключение, что присутствуют недоразведанность месторождения или недостаток петрофизического обеспечения. Это, в свою очередь, должно привести к планированию и осуществлению дополнительного комплекса геолого-технических мероприятий.
Выводы
Построенная математическая модель распределения достоверности петрофизических параметров позволяет получить результат в форме последовательности α-сечений. Структура α-сечений объективно отражает информационную обеспеченность геологической модели исходными данными. Это, в свою очередь, дает возможность определять риски перед введением в эксплуатацию нефтегазового месторождения, а также выделять зоны недоразведанности, что позволяет составлять актуальный план работ по доразведке месторождений.
Библиографическая ссылка
Кожевникова П.В., Кунцев В.Е., Дорогобед А.Н., Мотрюк Е.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ДОСТОВЕРНОСТИ ПЕТРОФИЗИЧЕСКИХ ПАРАМЕТРОВ ПРИ ПОСТРОЕНИИ ГЕОЛОГИЧЕСКОЙ МОДЕЛИ // Современные наукоемкие технологии. – 2021. – № 2. – С. 31-37;URL: https://top-technologies.ru/ru/article/view?id=38490 (дата обращения: 19.04.2024).