Исследование температурного поля в цилиндрических каналах имеет широкое практическое применение. В частности, необходимость проведения термометрических измерений возникает в различных геофизических задачах (например, термометрия может быть использована для выявления интервалов заколонной циркуляции). Данному эффекту подвержено большинство эксплуатируемых скважин, и доля воды в добываемой нефти может достигать 90 %. Своевременное выявление таких интервалов позволяет ограничиться проведением текущего ремонта вместо капитального, что ведет к значительной экономии средств (до 400 %), и повысить вероятность успешного завершения ремонта [1, 2].
Чаще всего методы скважинной термометрии используются для диагностики нефтяных скважин с целью обнаружения интервалов заколонной циркуляции [3, 4]. Эти методы не учитывают различные эффекты (например, когда радиус скважины изменяется или возможно возникновение турбулентности в нефтяном потоке) [5, 6]. Далее предлагается программное средство, позволяющее моделировать температуру при ламинарном режиме течения, что позволяет, в свою очередь, основываясь на анализе температурного поля нефти в скважине, выделить ламинарный режим течения нефти в других эффектах.
Основные теоретические положения
Математическая модель, состоящая из уравнения теплопроводности для окружающей скважину породы, уравнения конвективной теплопроводности для потока нефти и начальных и граничных условий для температуры и тепловых потоков нефти и окружающей среды, описана в работах [7]. Данная модель позволяет рассчитывать распределение температуры для ламинарных и турбулентных потоков жидкости в цилиндрических каналах. Решение поставленной задачи может быть осуществлено с помощью «в среднем точного» асимптотического метода.
Турбулентное поле скоростей в потоке нефти может быть описано на основе уравнений Сполдинга:
,
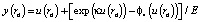где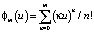 
, κ = 0,407, E = 10, τ0 – касательное напряжение. Профиль скорости турбулентного потока зададим в виде
,
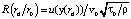где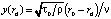 
. Величина τ0/ρ получена из уравнения Кармана–Никурадзе
,
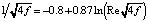где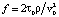 
. При разработке комплекса были созданы классы с данными формулами на языке C#, также были использованы функции из пакетов Math.net.
Основными используемыми уравнениями для описанной задачи являются уравнения теплопроводности в окружающем цилиндрический канал массиве породы (1) и конвективной теплопроводности потока жидкости с источниками внутри цилиндрического канала (2):
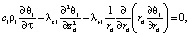(1)
rd > r0, 
,
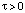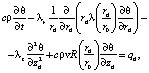(2)
где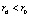 
, 
.
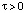На границе между скважиной и массивом породы должно соблюдаться равенство тепловых потоков и температур:
,
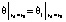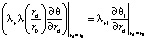. (3)
Начальная температура по времени определяется постоянным геотермическим коэффициентом для окружающей скважину породы, что означает линейный характер зависимости от глубины. Значение температуры отдаленных участков окружающей среды также определяется геотермической температурой:
,
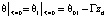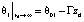. (4)
В точке zd = 0 температура потока изменяется по заданному закону:
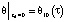. (5)
Задача также содержит некоторые дополнительные условия по zd, однако они здесь опущены вследствие того, что вторыми производными по zd пренебрегается из-за малого коэффициента, равного квадрату отношения радиуса скважины к ее глубине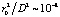 
.
Отличием описанной математической модели является учет турбулентной составляющей теплопроводности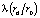 
и турбулентного профиля скорости 
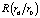, полученных на основе уравнений Сполдинга. Возможность получения аналитико-численного решения данной задачи, содержащей нелинейные коэффициенты, обеспечивает «в среднем точный» асимптотический метод [8].
Решение в нулевом приближении, описывающее среднюю температуру в пласте, представляется в форме:
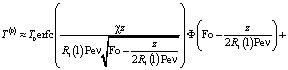
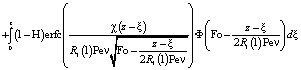. (6)
Функция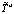 
представится в виде:
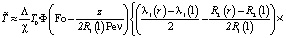
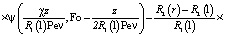
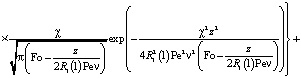
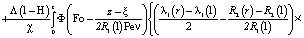
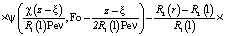
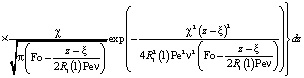. (7)
В настоящее время широкое распространение получили различные системы автоматизации расчетов. В статье описаны этапы разработки макета системы, позволяющие упростить процесс интерпретации скважинных термограмм.
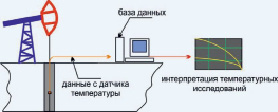
Рис. 1. Схема взаимодействия программного комплекса со средствами температурных исследований
Основная идея работы модуля представлена на рис. 1. Для его успешного функционирования необходима слаженная работа нескольких компонентов. Это источники данных (датчики, опущенные на определенную глубину в скважине), средство передачи данных – беспроводное и проводное (например, через сетевой кабель или непосредственно через кабель на запоминающее устройство), база данных, вычислительное устройство, поддерживающее NET.Framework.
Программный комплекс для такого модуля должен эффективно работать с базами данных, при этом быть высокопроизводительным. Поэтому для его реализации был выбран язык программирования C#. Осуществление функционала системы управления базами данных взяла на себя компактная и встроенная в платформу программа VisualStudioSQLite.
Теоретическая кривая строится в несколько этапов.
1. Выгрузка параметров скважины из базы данных. Программный комплекс предоставляет возможность работы с несколькими месторождениями и скважинами. Каждая скважина закреплена за своим месторождением и обладает собственными параметрами, которые необходимы для определения характера поведения теоретической кривой. Для расчета температурных кривых заданы следующие значения параметров скважины и окружающих пород: D = 2000 м, r0 = 0,1 м, Γ = 0,02 K/м, с1 = 950 Дж/(К*кг), ρ1 = 2000 кг/м3, λ1 = 0,67 Вт/(м*К); предполагается, что скважина заполнена нефтью с параметрами с = 2000 Дж/(К*кг), ρ = 900 кг/м3, λ = 0,15 Вт/(м*К), μ = 0,038 мПа*с [9].
2. Заполнение текстового поля «zd». Пользователь указывает значение в этом текстовом поле для задания программному комплексу глубины («zd»), относительно которой нужно калибровать построение кривой.
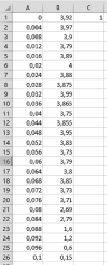
Рис. 2. Пример экспериментальных значений в Excel-файле
После нажатия на кнопку «Построение теоретической кривой» производится расчет и выводится график по полученным результатам. Для осуществления данного этапа программный комплекс обращается к прописанным функциям и процедурам, отвечающим за математический расчет температурных полей. На основе внешней библиотеки ZedGraph отображается график с кривой.
Для построения экспериментальной кривой необходимо импортировать Excel-файл, хранящий результаты температурных измерений в скважине. После импорта данные вносятся в БД для возможности их использования в будущем (выборка осуществляется по дате импорта значений).
На рис. 2 изображен пример обрабатываемых экспериментальных данных. Здесь первый столбец отображает значения для параметра «zd», второй – для «τ».
Рис. 3 иллюстрирует архитектуру программного комплекса. На нем отображены элементы вычислительной системы и связи между ними, показаны потоки данных. Сплошными линиями отображены связи между внешними источниками и местами хранения данных и программным обеспечением, штрихованными линиями показаны данные, полученные в результате работы ПО.
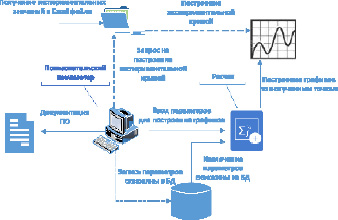
Рис. 3. Архитектура ПО
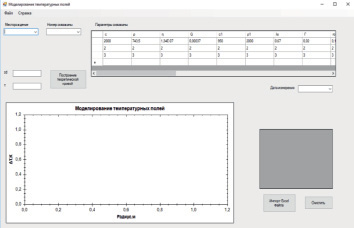
Рис. 4. Интерфейс ПО. Представлены поля для ввода данных, формируемые таблицы и управляющие кнопки. В поле вывода в результате работы программы отображаются температурные поля скважины в виде двумерных графиков
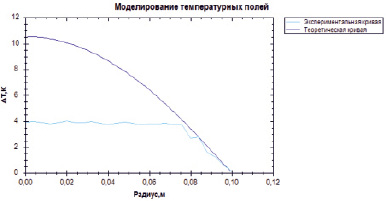
Рис. 5. Результат работы программного комплекса
На рис. 4 изображен интерфейс ПО. Он представляет собой форму, которая позволяет выбрать из списка месторождение и скважину, в таблицу справа вводятся или загружаются параметры скважины. В полях ввода задаются значения для параметров «zd» и «τ». После нажатия на кнопку «Построение теоретической кривой» в нижней части формы появляются кривые температурных полей и таблица с расчетными данными.
Результаты применения описанной методики показаны на графике (рис. 5). Представлены две кривые, при помощи которых пользователь способен самостоятельно провести анализ ламинарного течения.
Основными перспективами развития описанного модуля являются:
– добавление функций анализа данных динамики происходящих в скважине температурных процессов с целью прогнозирования нежелательных ситуаций и своевременного их устранения;
– учет дополнительных эффектов, не связанных с изменением режима течения.
Выводы
Созданная демонстрационная версия модуля моделирования турбулентного и ламинарного режима течения в скважине позволяет выделять ламинарный режим при интерпретации результатов температурных исследований, проводимых на скважинах, тем самым повысив точность данного процесса. Повышение точности интерпретации скважинных термограмм может способствовать значительной экономии средств на обслуживание действующих нефтяных скважин.
Авторы выражают особую благодарность д.т.н. А.И. Филиппову и д.т.н. О.В. Ахметовой за неоценимую помощь при разработке формул, положенных в основу расчетов.
Библиографическая ссылка
Ишмухаметова А.А., Левина Т.М., Родионов А.С., Фархутдинов Р.И., Хусаинов И.Р. ПРОГРАММНОЕ СРЕДСТВО ДЛЯ МОДЕЛИРОВАНИЯ РАДИАЛЬНОГО РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ В СКВАЖИНЕ // Современные наукоемкие технологии. – 2021. – № 2. – С. 19-24;URL: https://top-technologies.ru/ru/article/view?id=38488 (дата обращения: 25.04.2024).