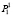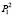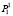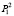Математические модели, для построения которых используется аппарат теории массового обслуживания, имеют широчайшее применение в самых различных исследовательских и прикладных задачах. Анализ работы сложных телекоммуникационных систем [1–3], решение задач управления материальными и информационными потоками [4–7], оптимизация логистических структур и т.п. Кроме классических моделей с пуассоновскими потоками, известны и достаточно обстоятельно исследованы модели с групповым обслуживанием заявок [8], модели с ограниченным временем жизни заявок [9–10], так называемые поллинговые системы [11–13], в которых одно устройство обслуживания принимает заявки из нескольких независимо друг от друга формирующихся очередей и ряд других. В подавляющем большинстве случаев при построении моделей принимается гипотеза об эквивалентности всех обслуживающих устройств (каналов обслуживания), входящих в состав системы. На самом деле это, конечно, не так. Невозможно набрать бригаду рабочих абсолютно одинаковой квалификации или сформировать парк автопредприятия из машин, обладающих одинаковой грузоподъёмностью и скоростью и т.п. Наоборот, разнообразие рабочих органов сообщает системе гибкость в управлении и вариативность. Если различия между интенсивностями работы каналов невелики, то, как правило, ими можно пренебречь, не нанося при этом ущерба адекватности модели. Однако в тех случаях, когда возможности рабочих органов системы массового обслуживания существенно различны, эти различия должны быть обязательно учтены в ходе математического моделирования, в противном случае полученные результаты, скорее всего, будут недостоверны.
Рассмотрим систему массового обслуживания, имеющую n независимых каналов, на вход которой поступает пуассоновский поток заявок интенсивности λ. Потоки заявок, покидающих систему, также являются пуассоновскими, а интенсивности их для разных каналов различны и равны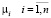 
. Будем полагать, что заявки попадают в любой свободный канал с одинаковой вероятностью. Граф такой системы представлен на рис. 1. Числа в левой части прямоугольников имеют смысл количества каналов, задействованных в обслуживании в данный момент, а в правой части – номера этих каналов. Поскольку каналы неэквивалентны, это суть различные состояния. Весовые коэффициенты ребер имеют смысл интенсивностей соответствующих потоков.
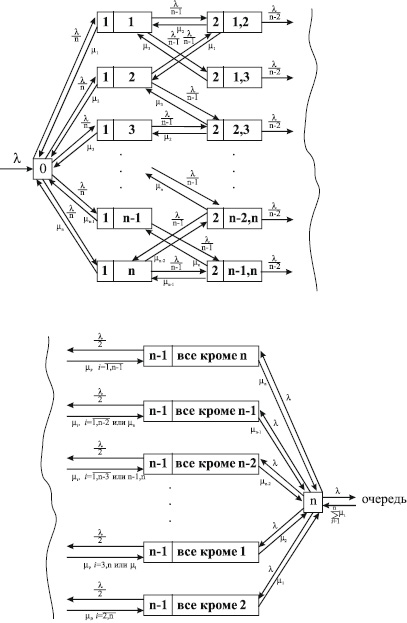
Рис. 1. Система массового обслуживания с n каналами разной производительности и равновероятным распределением входного потока
Обращаясь к рис. 1, заметим, что число различных состояний системы быстро растет с увеличением количества каналов. Выделим из множества всех возможных состояний системы подмножества, характеризующиеся одинаковым числом занятых каналов и назовем их наборами состояний.
Количество элементов в составе набора, где число занятых каналов равно k, находится с помощью известной комбинаторной формулы
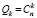, (1)
где n – общее число рабочих органов (каналов) системы массового обслуживания; k – номер набора состояний.
Для системы с отказами, не предусматривающей накопление очереди, общее число возможных состояний системы Q определится как
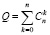, (2)
Именно это соотношение будет определять размерность системы обыкновенных дифференциальных уравнений Колмогорова, которая используется для математического описания поведения систем массового обслуживания с пуассоновскими потоками.
Аналитическое исследование систем такого типа с большим количеством каналов затруднительно, несмотря на наличие модели, в силу очевидных технических сложностей. Здесь мы ограничиваемся анализом решений, полученных для стационарного состояния двухканальной системы массового обслуживания с рабочими органами различной интенсивности.
Прежде всего заметим, что наличие различий между рабочими органами значительно повышает роль управления входным потоком заявок, которое предполагает отыскание наиболее рационального распределения входного потока заявок между каналами обслуживания. Ниже представлены три возможные схемы администрирования и системы уравнений Колмогорова для отыскания вероятностей стационарных состояний.
1. Поступление заявок на оба канала происходит с одинаковой вероятностью.
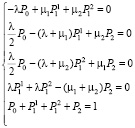, (3)
где P0 – вероятность того, что система свободна;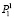 
– вероятность того, что в системе одна заявка и ее обслуживанием занят канал с интенсивностью μ1; 
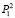– вероятность того, что в системе одна заявка и ее обслуживанием занят канал с интенсивностью μ2; P2 – вероятность того, что на обслуживании находятся две заявки и, так как накопление очереди не предусмотрено, P2 = Pотк. Граф распределения потоков по такой схеме для случая n каналов представлен на рис. 1.
2. Вероятности поступления заявок в каналы облуживания пропорциональны интенсивностям потоков обслуживания соответствующих каналов.
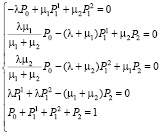, (4)
Граф распределения потоков по такой схеме представлен на рис. 2.
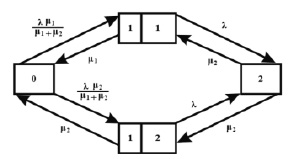
Рис. 2. Распределение потоков пропорционально их интенсивности
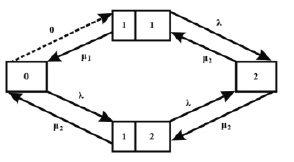
Рис. 3. Распределение потоков с приоритетом на «сильный» канал
3. Если оба канала свободны, поступившая заявка отправляется на «сильный» канал. (Приоритет «сильного» канала).
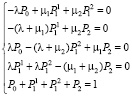, (5)
Граф распределения потоков по такой схеме представлен на рис. 3.
Системы уравнений (3)–(5) были использованы для сравнительной оценки возможностей всех вышеописанных схем администрирования при различных соотношениях интенсивностей рабочих органов. Для обеспечения корректности сравнения интенсивности входных потоков заявок λ выбирались так, чтобы величина нагрузки на систему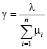 
оставалась неизменной и равной 0,8. Результаты вычислений сведены в табл. 1.
Таблица 1
Вероятности стационарных состояний двухканальной системы с отказами
|
λ = 4 μ1 = 1 μ2 = 4 |
λ = 7,2 μ1 = 1 μ2 = 8 |
λ = 10,4 μ1 = 1 μ2 = 12 |
Случай одинаковых каналов |
|||||||
|
Схема 1 |
Схема 2 |
Схема 3 |
Схема 1 |
Схема 2 |
Схема 3 |
Схема 1 |
Схема 2 |
Схема 3 |
||
|
P0 |
0,182 |
0,205 |
0,224 |
0,121 |
0,152 |
0,163 |
0,090 |
0,120 |
0,127 |
0,2577 |
|
|
0,364 |
0,315 |
0,276 |
0,434 |
0,383 |
0,363 |
0,467 |
0,420 |
0,408 |
0,2062 |
|
|
0,091 |
0,126 |
0,155 |
0,054 |
0,089 |
0,102 |
0,039 |
0,070 |
0,077 |
0,2062 |
|
P2 |
0,363 |
0,354 |
0,345 |
0,391 |
0,376 |
0,372 |
0,404 |
0,390 |
0,388 |
0,3299 |
В процессе анализа материалов табл. 1 обращает на себя внимание значительная диспропорция загруженности каналов обслуживания, заметно возрастающая с увеличением различий интенсивностей потоков обслуживания. Так, при распределении входного потока заявок по схеме 1 и величины отношения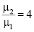 
время работы «слабого» канала оказывается примерно в 1,6 раза больше «сильного». По мере увеличения отношения 
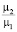различие нарастает и при 
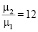приближается к 2. Использование других схем администрирования позволяет уменьшить диспропорцию при 
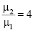до 1,25 раза, а при 
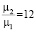– до 1,7 раза, но не устранить полностью. Это может оказаться существенным и повлиять на работоспособность системы, если рабочие органы имеют элементы, характеристики которых подвержены временному дрейфу, или требуют длительной настройки и регулярного профилактического ремонта.
Неэквивалентность каналов заметно влияет и на технико-экономические показатели. Так, если для системы с каналами одинаковой интенсивности доля потерянных заявок равна примерно 33 %, то при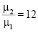 
она достигнет 40 % и практически не корректируется с помощью рассмотренных приемов администрирования. Это ставит под сомнение целесообразность объединения в систему каналов, интенсивность работы которых существенно различна.
В рамках данной работы авторы ограничились только рассмотрением систем с отказами, не имеющими опции накопления очереди, поскольку в системах с ожиданием доля обслуженных заявок растет по мере увеличения допустимого числа мест в очереди независимо от свойств каналов обслуживания. При отсутствии ограничений на длину очереди и выполнении условия γ < 1 все заявки рано или поздно будут обслужены, т.е. Pотк. = 0 для любого соотношения интенсивностей потоков обслуживания.
Представляет интерес вопрос о том, как изменяются эксплуатационные характеристики системы с неэквивалентными каналами при изменении величины нагрузки γ. С помощью модели (3)–(5) были вычислены вероятности стационарных состояний системы, находящейся в «недогруженном» положении: γ = 0,4 и «перегруженной» системы: γ = 1,6. Результаты расчетов представлены в табл. 2.
Таблица 2
Вероятности стационарных состояний двухканальной системы при различной нагрузке
|
µ1 = 1 µ2 = 4 λ = 2 γ = 0,4 |
µ1 = 1 µ2 = 4 λ = 8 γ = 1,6 |
|||||||
|
Схема 1 |
Схема 2 |
Схема 3 |
одинаковые каналы |
Схема 1 |
Схема 2 |
Схема 3 |
одинаковые каналы |
|
|
P0 |
0,364 |
0,417 |
0,461 |
0,471 |
0,071 |
0,078 |
0,082 |
0,107 |
|
|
0.363 |
0,278 |
0,205 |
0,189 |
0,286 |
0,266 |
0,251 |
0,172 |
|
|
0,091 |
0,139 |
0,180 |
0,189 |
0,071 |
0,089 |
0,102 |
0,172 |
|
P2 |
0,182 |
0,166 |
0,154 |
0,151 |
0,571 |
0,567 |
0,565 |
0,549 |
Из материалов таблицы видно, что с увеличением загруженности системы наблюдается ощутимое снижение диспропорции загруженности «слабого» и «сильного» каналов. В условиях малой нагрузки (γ = 0,4), отношение вероятностей загруженности слабого канала к сильному при работе по схеме 1 равно 2. С увеличением γ до 0,8 это отношение снижается до 1,6, а при γ = 1,6 оно составляет 1,33. Вместе с тем при малых значениях нагрузки существенно возрастает эффект администрирования в рамках предложенных вариантов перераспределения потока поступающих в систему заявок. Особенно отчетливо это проявляется на показателе P0, характеризующем долю времени, в течение которого система свободна.
Заключение
1. На базе системы уравнений Колмогорова дано математическое описание поведения систем массового обслуживания с неэквивалентными каналами, функционирующими в режиме пуассоновских потоков.
2. Определены эксплуатационные характеристики двухканальной системы для различных соотношений интенсивностей обслуживания и величины общей нагрузки на систему
3. Предложены схемы администрирования, позволяющие снизить диспропорцию загруженности каналов, которая возникает вследствие их неэквивалентности.
4. Показана нецелесообразность объединения в составе системы каналов, значительно различающихся по показателю интенсивности обслуживания.
Библиографическая ссылка
Нуриев Н.К., Печеный Е.А., Старыгина С.Д. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С КАНАЛАМИ РАЗНОЙ ПРОИЗВОДИТЕЛЬНОСТИ // Современные наукоемкие технологии. – 2021. – № 1. – С. 31-36;URL: https://top-technologies.ru/ru/article/view?id=38467 (дата обращения: 03.12.2024).