В руководящих документах Министерства образования [1] и учебного заведения [2] устанавливается порядок оценивания успеваемости студентов как в четырехбалльном виде («отлично», «хорошо», «удовлетворительно» и «неудовлетворительно»), так и в двузначном виде («зачет» и «незачет»). Базовым можно считать двузначный вид, а четырехбалльный – его расширением.
В разделе «Фонд оценочных средств» образовательных программ необходимо формулировать критерии оценивания знаний студентов, очевидно, что критерий оценивания должен быть ясным и не допускающим двусмысленного толкования. Однако ни методика формулирования, ни оценка качества критериев нигде не регламентированы.
В работе рассмотрены рабочие программы нескольких дисциплин Уфимского государственного нефтяного технического университета (УГНТУ) для потока БТК-16 («Основные процессы химических производств и химическая кибернетика», год приема 2016) [2] и выделены в них критерии оценивания. Проведен анализ данных критериев и оценка семантической близости между ними. Были использованы метрики, которым на вход подается выражение в векторном виде.
Постановка задачи
Векторные представления слов получили широкое распространение в обработке естественного языка. Они помогают вычислять семантическое расстояние между словами или высказываниями. Последние модели векторных представлений выражают слова или предложения в векторном виде с учетом контекста. Это в свою очередь повышает точность расчета расстояний, поскольку смысл используемых слов зависит от контекста. Среди данных моделей можно выделить ELMO, BERT [3, 4]. Первые же модели векторного представления учитывали лишь частоту встречаемости слов или символов. Если слово имело синонимы, то учитывалось только одно из значений, что могло сильно ухудшить результат [5–8].
В данной работе предполагается расчет и оценка возможности применения метрик семантического расстояния для критериев оценивания в различных рабочих учебных программах. Были использованы метрики, основанные на векторном представлении текста, такие как косинусная мера, скалярное произведение, евклидово расстояние, манхэттенское расстояние, расстояние Минковского. Существуют также метрики, которые учитывают частоту символов или слов (коэффициент Жаккара, коэффициент Танимото, мера Дайса, коэффициент Симпсона), а также метрики редакционного расстояния (расстояние Левенштейна, расстояние Джаро). Однако в работе они не будут использованы, поскольку вход для этих метрик не учитывает контекст и многозначность слов. Для оценки качества работы метрик семантической близости используют такие характеристики, как точность, полнота и F-мера. В работе [9] представлено описание данных характеристик и основные формулы, в работе [10] сравниваются различные метрики семантической близости. По результатам видно, что коэффициент Жаккара значительно уступает в точности косинусной мере. Работа [11] иллюстрирует, что при измерении семантического сходства с помощью метрик, основанных на частоте встречаемости символов или слов, в среднем F-мера составляет 60 %.
Для создания векторного представления используется предобученная модель ELMO для русского языка от DeepPavlov [12]. Данная модель использует алгоритм Embeddings from Language Models [3].
Модель ELMO отличается от традиционных векторных представлений тем, что каждый токен (более мелкая часть текста [3]: для абзаца это предложение, для предложения это слово, для слова это символ) этого представления является функцией от всего входного предложения. То есть, чтобы присвоить вектор слову, модель оценивает все выражение. Это так называемое контекстное представление, которое предполагает, что вектор не является фиксированным для токена.
Итак, имеются два вектора 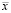 и
и 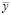 . Необходимо оценить расстояние между ними.
. Необходимо оценить расстояние между ними.
Евклидово расстояние между двумя точками в плоскости или n-мерном пространстве измеряет длину отрезка, соединяющего эти точки. Формула для расчета евклидова расстояния:
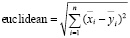 . (1)
. (1)
Метрика манхэттенского расстояния для двух точек в пространстве вычисляется следующим образом:
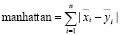 . (2)
. (2)
Расстояние Минковского является обобщением евклидова и манхэттенского расстояний. Оно определяется как
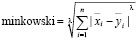 , (3)
, (3)
где λ – это натуральное число, такое, что λ ≥ 1.
При λ = 1 расстояние Минковского равно манхэттенскому расстоянию. При λ = 2 оно равно евклидову расстоянию. На практике используют λ = 1 и λ = 2. В работе [13] наглядно проиллюстрировано, как с возрастанием λ точность расчета снижается, и рекомендовано использовать, начиная с λ = 2, четные значения параметра λ.
Косинусная мера – метрика, которая вычисляет косинус угла между векторами. Диапазон изменения значений от 0 до 1, где 0 – отсутствие сходства, близости, а 1 – полное сходство. Вычисляется показатель по следующей формуле:
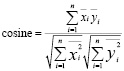 . (4)
. (4)
В качестве метрики близости иногда используют также и скалярное произведение векторов.
Евклидово, манхэттенское расстояние и расстояние Минковского представляют собой меры расстояния, а косинусная мера, скалярное произведение – это степени близости [14]. Меры расстояния являются фактическим расстоянием между точками в пространстве, поэтому они могут изменяться от 0 до бесконечности. Степени близости измеряются в долях от 0 до 1.
Расчет семантического расстояния между критериями оценивания
При рассмотрении рабочих программ можно выделить в них два типа используемых критериев оценивания: процентное (числовое) содержание работы и развернутое текстовое описание. В табл. 1 представлены критерии первого типа, а в табл. 2 – критерии второго типа. Критерии оценивания были выбраны с учетом наибольшей полноты описания работы и соответствующих для каждой дисциплины компетенций.
В критериях оценивания табл. 1 обращает свое внимание использование процентных отношений либо долей. Достоинством данных критериев является то, что они универсальны, тем не менее возникает вопрос, что есть полный объем знаний.
В табл. 2 используется развернутое текстовое описание. Однако при детальном рассмотрении видно, что они все равно ссылаются на некоторый объем, который надо знать, и словесно описывают доли знания этого полного объема (жирным выделено данное соотношение).
Таблица 1
Процентный (числовой) вид критериев оценивания
|
Оценка |
Критерий |
|
1. Аналитическая химия (АХ) |
|
|
5 |
Объем положительных ответов не менее 90 %; студент правильно излагает законы, понятия, обосновывает их и умеет применять для решения проблемных задач |
|
4 |
Объем положительных ответов не менее 80 %; студент правильно излагает законы, понятия, обосновывает их и умеет применять для решения конкретных задач |
|
3 |
Объем положительных ответов составляет не менее 60 %; студент правильно излагает основные законы, понятия |
|
2 |
На все вопросы отвечает поверхностно или не по существу; не может решить задачи даже с помощью преподавателя; не продемонстрировал теоретических знаний, необходимых для решения задач |
|
2. Теоретические основы химической технологии топлива и углеродных материалов (ТОХТ) |
|
|
5 |
Полное выполнение задания без ошибок или с незначительными арифметическими ошибками (задание выполнено не менее чем на 90 %) |
|
4 |
Есть незначительные ошибки и задание выполнено не менее чем на 75 % |
|
3 |
Выполнение задания более 60 %, но менее 75 % |
|
2 |
Задание не выполнено или выполнение задания менее 60 % |
|
3. Общая и неорганическая химия (ОНХ) |
|
|
5 |
Дан исчерпывающий ответ на все вопросы задания |
|
4 |
Дан ответ на 80 % вопросов в задании |
|
3 |
Дан правильный ответ на 60–79 % вопросов задания |
|
2 |
Дан ответ на менее чем 60 % вопросов задания |
Таблица 2
Текстовый вид критериев оценивания
|
Оценка |
Критерий |
|
1. Безопасность жизнедеятельности (БЖД) |
|
|
5 |
Показал всестороннее, систематическое и глубокое знание учебного материала, предусмотренного программой по ГОС; усвоил основную и знаком с дополнительной литературой по программе; усвоил взаимосвязь основных понятий дисциплины; умеет творчески и осознанно применять полученные знания к анализу и решению практических задач |
|
4 |
Обнаружил полное знание учебного материала, предусмотренного программой; успешно ответил на все вопросы экзаменационного билета с одним небольшим недочетом; усвоил основную литературу, рекомендованную программой дисциплины, способен к самостоятельному пополнению и обновлению знаний в ходе дальнейшей профессиональной деятельности |
|
3 |
Обнаружил знание основного учебного материала, предусмотренного программой, в объеме, необходимом для работы по специальности, знает основную литературу, рекомендованную программой; справился с выполнением заданий, предусмотренных программой, но допустил погрешности в ответе на экзамене; обладает необходимыми знаниями для их устранения под руководством преподавателя |
|
Окончание табл. 2 |
|
|
Оценка |
Критерий |
|
2 |
Обнаружил пробелы в знании основного материала, предусмотренного программой, допустил принципиальные ошибки при ответе на экзаменационные вопросы, не выполнил отдельные задания, предусмотренные формами текущего контроля. Ответ студента на экзамене свидетельствует о том, что он не может продолжить обучение или приступить к профессиональной деятельности по окончании вуза без дополнительных занятий по соответствующей дисциплине |
|
2. Системы управления химико-технологическими процессами (СУХТП) |
|
|
5 |
Ответы на поставленные вопросы излагаются логично, последовательно и не требуют дополнительных пояснений. Делаются обоснованные выводы. Демонстрируются глубокие знания учебного материала. Соблюдаются нормы литературной речи |
|
4 |
Ответы на поставленные вопросы излагаются систематизированно и последовательно. Материал излагается уверенно. Демонстрируется умение анализировать материал, однако не все выводы носят аргументированный и доказательный характер |
|
3 |
В последовательности изложения допускаются неточности. Демонстрируются поверхностные знания вопроса, с трудом решаются конкретные задачи. Имеются затруднения с выводами |
|
2 |
Материал излагается непоследовательно, сбивчиво, не представляет определенной системы знаний по дисциплине. Не проводится анализ. Выводы отсутствуют. Ответы на дополнительные вопросы отсутствуют |
|
3. Дискретная математика (ДМ) |
|
|
5 |
Студент показывает всестороннее и глубокое знание программного материала, умение свободно выполнять задание и решать задачи по программе курса, проявляет творческие способности в понимании, изложении и применении учебного материала |
|
4 |
Студент показывает полное знание программного материала, способен к самостоятельному выполнению и обновлению знаний в ходе дальнейшей учёбы и профессиональной деятельности |
|
3 |
Студент показывает знание основного учебно-программного материала в объёме, необходимом для дальнейшей учёбы и профессиональной деятельности, но не в полной мере справляется с выполнением заданий, предусмотренных программой |
|
2 |
Студент показывает пробелы в знании основного учебно-программного материала, допускает принципиальные ошибки в выполнении предусмотренных программой заданий |
Можно сделать вывод, что процесс создания критериев оценивания никак не формализован. Поэтому процедура оценивания становится неформальной, зависящей от опыта и квалификации преподавателя, следовательно, возникает потребность в формализации этих критериев, чтобы разница между ними была более или менее равномерной.
В работе проводится расчет с помощью выбранных метрик, семантической близости критериев оценивания. Целью является повышение качества критериев оценивания. Библиотека [12] предназначена для подключения в программный код на языке python, далее требуется ввести две фразы для расчета расстояния между ними.
На рис. 1–5 представлены результаты расчета расстояний между оценками «2» и «3», «2» и «4», «2» и «5» с помощью выбранных метрик семантической близости для рабочих программ дисциплин потока БТК-16. Значение расстояния между «2» и «2» для мер расстояния равно 0, а для степеней близости 1. Верхние графики соответствуют числовому виду критериев оценивания (табл. 1), нижние – текстовому (табл. 2). Из рисунков видно, что в случае мер расстояния значения равномерно возрастают, а в случае степеней близости – равномерно убывают.
На рис. 1 представлены результаты расчета семантической близости с помощью евклидова расстояния. Приведена аппроксимация полученных значений полиномом второго порядка, представлено уравнение полинома и значение среднеквадратического отклонения. Из графиков видно, что на параболическую кривую лучше ложатся результирующие точки дисциплин «Теоретические основы химической технологии» и «Дискретная математика».
На рис. 2 графически проиллюстрированы результаты расчета с помощью манхэттенского расстояния. Наилучшая аппроксимация результатов параболической кривой в данном случае достигается в тех же дисциплинах, что и на рис. 1.
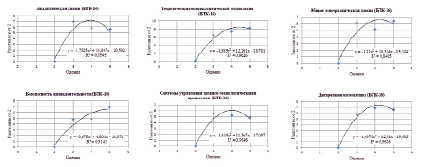
Рис. 1. Евклидово расстояние
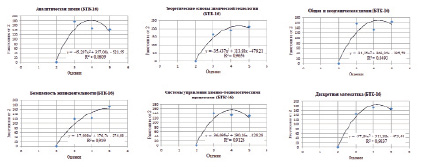
Рис. 2. Манхэттенское расстояние
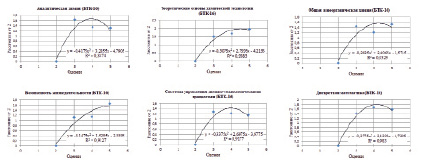
Рис. 3. Расстояние Минковского (λ = 4)
На рис. 3 расчет произведен с помощью расстояния Минковского при λ = 4. По аппроксимациям получены схожие с рис. 1 и 2 результаты. Однако графически значения расстояний имеют меньшую наглядность, так как трудно сказать, насколько далеко точки находятся друг от друга. Большей информативностью и наглядностью в этом плане обладают рис. 1 и 2. Также из полученных графиков можно сделать вывод, что значение R2 меньше, чем на рис. 1 и 2, однако разница несущественна.
На рис. 4 представлена аппроксимация результатов, рассчитанных с помощью косинусной меры, полиномом второго порядка. В данном случае также можно сделать вывод, что параболическая кривая лучше аппроксимировала результаты дисциплин «Теоретические основы химической технологии» и «Дискретная математика».
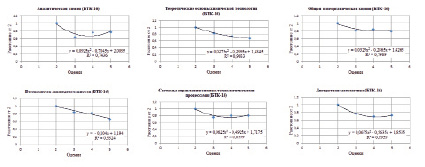
Рис. 4. Косинусная мера
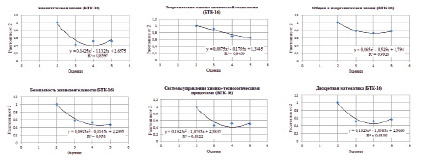
Рис. 5. Скалярное произведение
Результаты для метрики скалярного произведения иллюстрирует рис. 5. Здесь наилучшая аппроксимация достигается для дисциплин «Общая и неорганическая химия», «Теоретические основы химической технологии» и «Безопасность жизнедеятельности».
В табл. 3 сведены результаты для среднеквадратического отклонения, округленные до двух знаков после запятой.
Таблица 3
Значения коэффициента детерминации R2 при аппроксимации результатов полиномом второго порядка
|
Метрики |
АХ |
ТОХТ |
ОНХ |
БЖД |
СУХТП |
ДМ |
|
Евклидово расстояние |
0,85 |
0,96 |
0,84 |
0,91 |
0,91 |
0,98 |
|
Манхэттенское расстояние |
0,86 |
0,97 |
0,85 |
0,91 |
0,91 |
0,98 |
|
Расстояние Минковского |
0,85 |
0,96 |
0,83 |
0,91 |
0,92 |
0,98 |
|
Косинусная мера |
0,74 |
0,99 |
0,8 |
0,93 |
0,83 |
0,99 |
|
Скалярное произведение |
0,86 |
0,94 |
0,99 |
0,96 |
0,88 |
0,93 |
Из таблицы видно, что среднеквадратическое отклонение аппроксимации во многих случаях превышает 0,9 (в 2/3 примеров R2 больше, чем 0,9). При этом две последние метрики, соответствующие косинусной мере и скалярному произведению, имеют серьезные отклонения от первых трех. Эти метрики отличаются от остальных используемых тем, что они являются степенями близости. Наибольшее значение среднеквадратического отклонения аппроксимации наблюдается у дисциплин «Теоретические основы химической технологии» и «Дискретная математика», что также графически подтверждается рис. 1–5. При этом значение R2 для результатов косинусной меры в этих дисциплинах составляет 0,99.
У дисциплин «Аналитическая химия» и «Общая и неорганическая химия» большая часть значений R2 меньше 0,9. При их детальном рассмотрении можно увидеть, что у дисциплины «Аналитическая химия» оценка «2» описана словесно, хотя все остальные оценки описаны в числовом виде. У дисциплины «Общая и неорганическая химия» оценка «5» описана словесно при числовом описании остальных оценок. При этом у дисциплины «Теоретические основы химической технологии» почти все значения R2, кроме последнего, больше 0,95. Из табл. 1 видно, что все оценки у данной дисциплины имеют числовое (процентное) описание. Следовательно, можно сделать вывод, что отклонение от хороших аппроксимаций связано с тем, что критерии оценивания в дисциплинах «Аналитическая химия» и «Общая и неорганическая химия» являются смешанными. Поэтому необходимо описывать критерии оценивания либо только в числовом, либо только в текстовом виде.
По поводу дисциплин «Безопасность жизнедеятельности» и «Системы управления химико-технологическими процессами» можно сказать, что результаты указывают на то, что в сравнении с дисциплиной «Дискретная математика» критерии оценивания в них описаны менее корректно. При этом очевидно, что корректная словесная формулировка является более трудоемкой, чем числовая (процентная).
Из результатов табл. 3 можно заключить, что использование пяти метрик для расчета семантического расстояния является избыточным. Для первых трех метрик увеличение значения параметра λ практически не влияет на результат, при этом в работе [13] показано, что при λ = 1 точность расчета выше. Поэтому из мер расстояния для практических расчетов рекомендуется выбрать евклидово расстояние. Из степеней близости следует использовать косинусную меру, потому что в корректно описанных критериях оценивания данная метрика позволяет достичь значения R2 > 0,95. Скалярное произведение не рекомендуется использовать, поскольку в тех случаях, когда все остальные метрики дают невысокий результат, она дает высокий, и наоборот. Соответственно, имея две метрики (евклидово расстояние и косинусную меру), можно определить, насколько корректно составлен критерий оценивания, если значения R2 выбранных метрик больше 0,95, то рассматриваемый критерий составлен корректно. Полученные результаты носят качественный характер, поэтому аппроксимация всего по четырем точкам вполне допустима.
Заключение
По результатам расчета можно сделать следующие выводы:
- использование метрик семантической близости на критериях оценивания рабочих программ высших учебных заведений возможно;
- фактически результаты показывают, что от качества написания критериев оценивания расстояние не зависит, т.е. нет разницы, будут ли критерии описаны в числовом виде или же в развернутом текстовом, следовательно, нет смысла составлять критерии оценивания вручную, необходимо автоматизировать данный процесс;
- аппроксимация результатов расчета полиномом второго порядка дала хорошие результаты. Отклонения наблюдаются в тех случаях, когда критерии оценивания составлены не только в числовом, либо же текстовом виде, а наблюдается смешение типов критериев (одновременное и числовое, и текстовое описание).
Библиографическая ссылка
Гиниятуллин В.М., Салихова М.А., Хлыбов А.В., Чурилов Д.А., Чурилова Е.А. ОЦЕНКА СЕМАНТИЧЕСКОЙ БЛИЗОСТИ МЕЖДУ КРИТЕРИЯМИ ОЦЕНИВАНИЯ В РАБОЧИХ ПРОГРАММАХ ВУЗА // Современные наукоемкие технологии. 2021. № 1. С. 12-19;URL: https://top-technologies.ru/ru/article/view?id=38464 (дата обращения: 15.12.2025).
DOI: https://doi.org/10.17513/snt.38464



