Прогнозирование невозмущенного движения является приближением решения более сложной задачи – задачи долгосрочного прогнозирования движения ИСЗ (искусственного спутника Земли), в которой учитываются возмущающие факторы. Прогнозирование движения ИСЗ позволяет оценить космическую обстановку в зонах действия средств наземного наблюдения в любое наперед заданное время, предъявлять требования к точности измерительных средств, достоверности результатов прогнозирования.
Изучение задачи прогнозирования вызывает у будущих специалистов контроля космического пространства определенные трудности, связанные с большим объемом вычислений, высокими требованиями к математической подготовке, пространственному воображению. Компьютерное моделирование сложных процессов, реализующее представление объектов, характеризующих свойства системы и динамику ее изменения со временем, является лучшим выходом в такой ситуации [1; 2].
В образовательном процессе метод наглядности был и остается одинаково актуальным для изучения гуманитарных и технических дисциплин. Применение данного метода позволяет максимально задействовать зрительный анализатор для запоминания и последующего воспроизведения учебной информации.
Образовательные стандарты третьего поколения предполагают не передачу обучающимся установленного объема теоретических знаний и практических навыков, а овладение профессиональными компетенциями, т.е. способностью комплексного применения усвоенных знаний, умений и навыков. В научной и методической литературе широко освещаются как положительные эффекты использования электронных образовательных ресурсов, так и проблемы, связанные с их внедрением в процесс обучения на различных уровнях образования [3; 4].
К основополагающим знаниям будущих специалистов в области контроля космического пространства относятся сведения о законах движении ИСЗ в околоземном космическом пространстве. Без них невозможна дальнейшая профессиональная деятельность и совершенствование уровня профессионального мастерства.
Современные средства вычислительной техники и программные продукты, которые используются в образовательном процессе, позволяют существенно расширить возможности наглядного метода, а именно, провести моделирование и визуализацию различных процессов.
Для решения учебной задачи прогнозирования можно сделать следующие допущения: движение ИСЗ по орбите является невозмущенным (движение ИСЗ происходит в соответствии с основными законами механики, возмущающие факторы не учитываются); поверхность Земли является сферой (следовательно, географические координаты совпадают с геодезическими), высота стояния станции наблюдения равна нулю; считается, что ИСЗ попал в зону видимости станции наблюдения, если его угол места больше величины, характеризующей станцию.
Постановка задачи
Постановка прямой задачи прогнозиро- вания.
Пусть информационное средство С1 с географическими координатами (φ1, λ1) получило следующие данные об ИСЗ: в момент наблюдения t0 по московскому времени были определены топоцентрические сферические координаты спутника: азимут β0, угол места ε0 и дальность D0, а также скорости изменения координат Vβ, Vε, VD.
Требуется рассчитать координаты ИСЗ относительно наземного средства наблюдения потребителя С2 с известными географическими координатами (φ2, λ2) для фиксированных моментов времени в будущем.
Цель исследования: построение виртуального прибора, позволяющего по заданным данным рассчитывать координаты положения и скоростей ИСЗ в любой наперед заданный момент времени, относительно наземного средства наблюдения потребителя, визуализация решения задачи, анализ эффективности разработанной модели в учебном процессе.
Исходными данными для решения данной задачи являются:
– время t0 измерения координат ИСЗ, время начала расчета t1, интервал моделирования T;
– географические координаты (долгота и широта) информационного средства С1(φ1, λ1) и средства наземного наблюдения потребителя С2(φ2, λ2);
– характеристики средства наземного наблюдения потребителя: минимальные и максимальные значения угла места, азимута и дальности действия потребителя;
– топоцентрические сферические координаты спутника: азимут β0, угол места ε0 и дальность D0, а также скорости изменения координат Vβ, Vε, VD.
Алгоритм решения задачи
Алгоритм решения задачи состоит из нескольких этапов [5; 6].
На предварительном этапе рассчитываются элементы орбиты невозмущенного движения ИСЗ (большая полуось a, эксцентриситет e, угол наклонения орбит i, аргумент перигея ω, угол восходящего узла Ω, время прохождения ИСЗ через точку перигея), вектор состояния ИСЗ (x, y, z, Vx, Vy, Vz) в инерциальной системе координат. На этом же этапе проводится проверка корректности исходных данных.
В процессе моделирования для каждого момента времени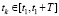 
выполняется следующая последовательность действий:
1) рассчитываются орбитальные координаты ИСЗ с помощью уравнения Кеплера;
2) выполняется пересчет орбитальных координат в топоцентрические координаты с центром в точке стояния средства наземного наблюдения потребителя;
3) определяется факт попадания ИСЗ в зону контроля средства потребителя С2.
Заключительный этап содержит вывод численных результатов, а также наглядную динамическую визуализацию процесса.
Выходными данными являются: элементы орбиты и вектор состояния ИСЗ, координаты и скорости изменения координат ИСЗ в прогнозируемые моменты времени в топоцентрической системе координат с центром в точке стояния средства потребителя С2, информация о попадании/непопадании ИСЗ в зону контроля средства С2, а также визуализированное изображение всего процесса.
Пример реализации алгоритма
Представляемая модель реализована в виде виртуального прибора в пакете программирования LabVIEW 15. Среда графического программирования LabVIEW позволяет с высокой степенью наглядности создавать виртуальные модели и отслеживать динамику процесса. Среда графического программирования LabVIEW находит применение в самых разнообразных сферах человеческой деятельности. Причинами столь широкого распространения пакета LabVIEW являются возможности не только проводить измерения, анализировать измеренные величины, отображать их на графиках и в отчетах, но и, используя программируемые логические контроллеры, осуществлять управление процессами. LabVIEW реализует концепцию графического программирования G, поэтому исходный код представляет собой блок-диаграмму, которая затем компилируется в машинный код. Поддержка выполнения кода, написанного на языке G, происходит в режиме потока данных, в то время как традиционные текстовые языки (например, C и C++) обеспечивают выполнение кода в виде последовательности команд.
На рис. 1 приведена лицевая панель виртуального прибора.
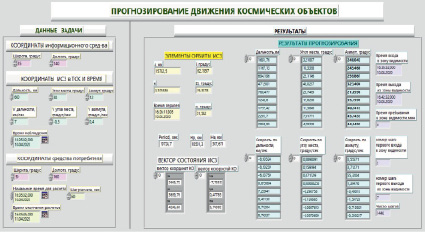
Рис. 1. Лицевая панель модели прогнозирования
В левой ее части задаются исходные данные:
– координаты информационного средства C1(35o, 140o);
– координаты ИСЗ, полученные информационным средством в топоцентрической системе координат с центром в точке C1 дальность D0 = 600 km, угол места ε0 = 300, азимут β0 = 120, скорости изменения координат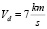 
, 
, 
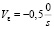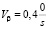; время наблюдения t0 10.04.2020 16:35,02;
– координаты средства наземного наблюдения потребителя C2(500, 1600) (по умолчанию зона действия средства строится по характеристикам дальности действия потребителя 20 тыс. км, значения угла места ε ≥ 10o);
– начальное время для расчета t1 10.04.2020 16:35,32;
– время окончания расчета 11.04.2020 16:35,42.
Правая часть отведена для вывода результатов. Заметим, что если данные задачи были введены некорректно, то появится всплывающее окно с надписью об ошибке. Найдены элементы орбиты
a = 15782.5 km, e = 0.577, i = 620.196, Ω = 190.339, ω = 510.582,
tпер = 10.04.2020 16:36,11
вектор состояния ИСЗ
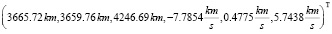
в абсолютной геоцентрической системе координат.
Результаты прогнозирования выводятся в виде таблиц изменения координат и скоростей их изменения с заданным шагом. Для расчета времени прохождения спутника через зоны действия средства наземного наблюдения необходимо рассчитать координаты точек пересечения орбиты космического объекта и конуса зоны действия средства (рис. 2).
Рис. 2. Орбита ИСЗ и конус зоны действия наземного средства наблюдения
Время входа входа/выхода в зону действия средства и время пребывания в зоне вычисляется исходя из сравнения полученных результатов по координатам угла места, а именно, как видно из таблицы изменения угла места ИСЗ ε = 100.3358 > 100 на первом шаге вычислений (отсчет начинается с нулевого шага) и ε = 70.3177 < 100 на седьмом шаге, т.е. время пребывания в зоне составляет семь минут.
Для того чтобы принять окончательное решение о попадании ИСЗ в зону действия оптической станции, нужно учесть время наблюдения, положение Солнца. Эту часть обучающимся предоставляется возможность сделать самостоятельно.
Для визуализации решаемой задачи (рис. 3) реализован модуль построения в виде Земного шара, орбиты ИСЗ в околоземном пространстве, места нахождения ИСЗ на орбите, зоны действия станции наземного наблюдения потребителя.
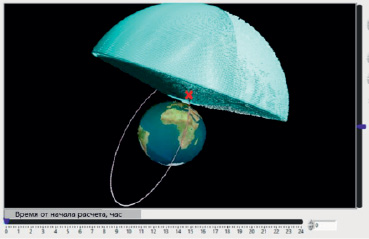
Рис. 3. Визуализация задачи прогнозирования движения ИСЗ
Для имитации работы станции наземного наблюдения потребителей информации используются конусообразные зоны действия с шаровым куполом, ограниченные по углу места. Положение ИСЗ на орбите отмечено красным цветом.
Ползунок слева от области построения позволяет увеличить/уменьшить масштаб построения. Двигая ползунок внизу картинки, можно увидеть передвижение ИСЗ по орбите на фоне вращения Земли вокруг своей оси, т.е. можно наблюдать картину входа – выхода ИСЗ в зону действия станции потребителя в динамике. Использование модели на учебных занятиях по изучению задачи прогнозирования позволяет получить глубокое понимание сути происходящих процессов.
Модель реализована в виде исполняемого файла *.exe. Однако если на компьютере не установлено LabVIEW или Run-Time Engine, файл с расширением .exe не стартует. Поэтому мы создали инсталлятор, куда включен Run-Time Engine и другие используемые компоненты.
Использование модели прогнозирования движения ИСЗ в учебном процессе обучения специалистов в области контроля космического пространства позволит углубить уровень понимания сути прогнозирования движения ИСЗ, и тем самым повысить качество усвоения учебного материала, поскольку даст возможность не выполнять громоздкие вычисления, а полностью сосредоточиться на анализе начальных данных и полученных результатов. Визуализация процесса развивает пространственное видение и делает обучение наглядным.
Разработанная модель была апробирована в образовательном процессе ВКА имени А.Ф. Можайского. Для определения ее эффективности были выбраны одна экспериментальная (ЭГ) и одна контрольная (КГ) группы, занятия в которых проводились без изменения тематического плана одним и тем же преподавателем. В ЭГ прогнозирование движения ИСЗ рассчитывалось и визуализировалось с помощью виртуального прибора, в КГ занятия проводились без его использования. Результаты текущего контроля показали, что в ЭГ процент положительных оценок был выше на 5 %, а процент хороших и отличных оценок – на 15 % выше, чем в КГ. После изучения материала было проведено анкетирование обучающихся в экспериментальной группе. Использование моделей, тренажеров способствует усвоению теоретического материала независимо от уровня подготовленности по дисциплине, что и отметили все опрошенные учащиеся.
Выводы
В данной статье описан разработанный авторами виртуальный прибор прогнозирования движения искусственного спутника Земли в околоземном космическом пространстве. Прибор состоит из двух блоков: вычислительного и блока построения. В вычислительном блоке рассчитывается положение ИСЗ на орбите в любой наперед заданный промежуток времени, время входа/выхода в зону/из зоны действия станции наземного наблюдения. Блок построения позволяет визуализировать траекторию движения ИЗС и границы действия станции наземного наблюдения. В работе проанализированы преимущества использования модели в образовательном процессе. Эффективность ее использования при обучении подтверждается результатами анкетирования и текущего контроля учащихся.
Библиографическая ссылка
Алдохина В.Н., Куликов С.В., Королев В.О. МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ В ОКОЛОЗЕМНОМ КОСМИЧЕСКОМ ПРОСТРАНСТВЕ // Современные наукоемкие технологии. – 2021. – № 1. – С. 7-11;URL: https://top-technologies.ru/ru/article/view?id=38463 (дата обращения: 21.11.2024).