В технологических процессах текстильной и лёгкой промышленности часто используется оборудование для размотки рулона как на этапе подготовительных работ, так и на этапе основного производства. Размотка рулона может осуществляться как непрерывно, так и с остановками для отмеривания необходимой длины. При размотке материала требуется обеспечить контроль ряда показателей, среди которых важнейшими являются скорость полотна и сила его натяжения. На эти показатели оказывают влияние некоторые факторы, среди которых присутствуют характеристики рулона (форма втулки, рулона, механические характеристики и состояние материала внутри рулона), характеристики системы размотки и системы управления, конструктивные особенности узла размотки. Какие-либо нарушения этих показателей, к примеру непостоянство силы натяжения полотна, могут привести к образованию петель, складок и т.п. Нарушение заданной скорости движения полотна сказывается как на силе натяжения, так и на колебаниях полотна, инициирующихся непосредственно рулоном.
При решении задач модернизации существующего оборудования проектируются новые системы управления устройств размотки. Следствием неидеальной формы рулона и погрешности установки рулона в машину является возникновение колебаний; очевидно, их параметры будут изменяться в процессе размотки ввиду изменений параметров рулона [1]. В проектируемой системе управления размоткой рулона должен обеспечиваться учёт указанных факторов.
В настоящей статье рассматривается задача разработки математической модели узла размотки с учётом геометрии втулки и рулона и расположения оси вращения втулки.
Материалы и методы исследования
В качестве примера рассмотрим узел размотки рулона, показанной на рис. 1, где 1 и 1' – пара разматывающих цилиндров, 2 – сенсорный вал, 3 – рулон, 4 – втулка, 5 – полотно материала. Обозначим: rн – радиус натяжения, rвр – радиус вращения, ω2 – угловая скорость рулона.
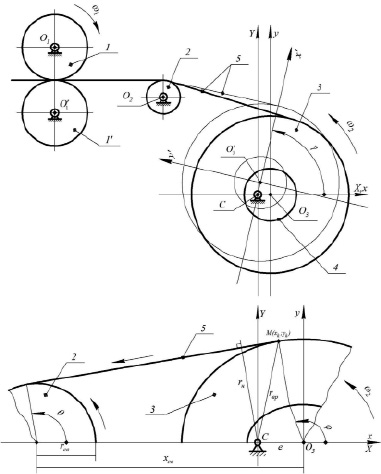
Рис. 1. Схема узла размотки рулона
Будем считать рулон абсолютно твёрдым телом, вращающимся вокруг неподвижной оси О3z, перпендикулярной плоскости рисунка. При размотке рулона на него действует сила натяжения F, создающаяся разностью скоростей рулона и пары разматывающих цилиндров, момент силы трения в подшипниках качения в опорах Mт и момент, создаваемый электродвигателем в режиме противовключения Mд. Для рассматриваемой расчётной схемы нетрудно записать [2]:
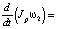
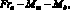(1)
где Jp – момент инерции рулона. Момент трения подшипника в первом приближении можно описать как произведение радиальной нагрузки Fr, радиуса подшипника и коэффициента трения; в свою очередь, радиальная нагрузка определяется массой рулона [3, 4]:
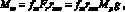(2)
где fт – коэффициент трения, rпш – радиус подшипника, Mр – масса рулона, g – ускорение свободного падения. Составлять уравнение будем относительно скорости рулона vр, для чего найдём её производную по времени:
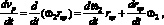(3)
объединяя (1), (2) и (3), после преобразований получаем
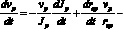
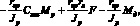(4)
где 
.
Момент инерции Jр является композицией функций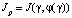 
. С учётом этого можно записать, что
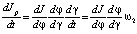. (5)
Аналогично выглядит выражение для производной от радиуса вращения. Подставим (5) в (4):
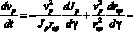
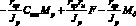. (6)
Получившееся выражение (6) является нелинейным дифференциальным уравнением первого порядка относительно vр. Для его решения создадим S-модель в пакете Simulink программы MATLAB (рис. 2) [5]. В S-модели Mд = 0.
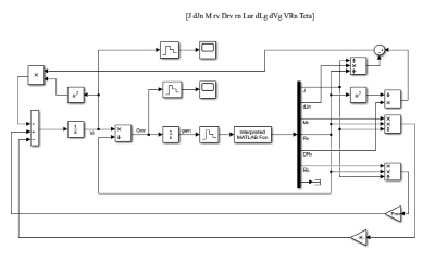
Рис. 2. S-модель
Для моделирования использовались следующие исходные данные: поперечное сечение втулки представлено эллипсом с полуосями 36,1 мм и 39,9 мм, rсв = 100 мм, xсв = 1 м, поверхностная плотность полотна 60 г/м2, ширина полотна 1,2 м, Mр = 700 кг, F = 500 H. На рис. 3 показан график vр(t) при начальном условии vр(0) = 5 м/с, что соответствует работе системы в режиме стабилизации.
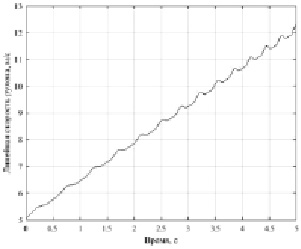
Рис. 3. Зависимость линейной скорости при vр(0) = 5 м/с
Нетрудно догадаться, что при отсутствии тормозного момента, создаваемого электродвигателем или иным каким механическим устройством, в условии сохранения постоянной силы натяжения скорость рулона должна непременно возрастать, что и продемонстрировано на рис. 3. В режиме стабилизации скорость и сила натяжения полотна должны быть постоянными во избежание, к примеру, обрыва вследствие неконтролируемой подачи. Применение законов управления с обратной связью исказит частотные характеристики, в связи с чем воспользуемся разомкнутым управлением, задав некое номинальное управляющее воздействие. Составим выражение момента электродвигателя постоянного тока с постоянными магнитами [6]:
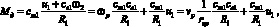(7)
где се1 – константа противо э.д.с., ст1 – постоянная момента, R1 – сопротивление обмотки статора, u1 – напряжение, подаваемое на обмотку статора, – управляющее воздействие. Подставим (7) в (6):
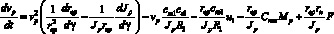. (8)
Уравнение (8) классифицируется как нелинейное и нестационарное, однако, строго говоря, в данной модели коэффициенты уравнения рассчитываются от угла поворота и ни прямой, ни неявной зависимости от времени нет. Можно свести уравнение (8) к нелинейному дифференциальному относительно γ(t), устранив тем самым нестационарность. Воспользуемся методом касательной линеаризации в окрестности номинального режима. Предварительно введём в рассмотрение номинальные, то есть желаемые значения регулируемых переменных и их отклонения: скорость –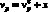 
и управляющее воздействие – 
; безусловно, отклонения распространяются и на γ(t) [7]:
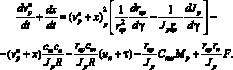(9)
Найдём значение номинального управляющего воздействия, для чего примем x = 0, τ = 0:
.
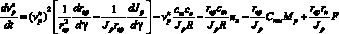Отсюда найдём
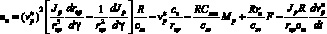. (10)
Результат моделирования при vр(0) = 5 м/с,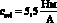 
, 
, 
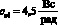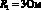показан на рис. 4.
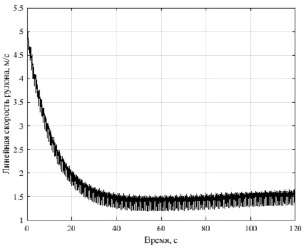
Рис. 4. Зависимость vр(t)
Как видно из рис. 4, учёт в математической модели Мд обеспечил начальную стабилизацию «неколебательной» составляющей.
В силу изменения параметров колебаний, для частотного анализа воспользуемся локальным оконным преобразованием Фурье (ОПФ) и построим спектрограмму скорости рулона [8]. Как известно, локальное ОПФ подвержено принципу неопределённости, согласно которому невозможно получить одновременно хорошее разрешение по частоте и по времени. Анализу подвергается часть сигнала, принадлежащего временному интервалу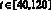 
с вычтенной полиномиально-аппроксимированной составляющей. Интервал квантования взят равным 0,001 с; частота дискретизации, следовательно, 1 кГц. Количество рассчитываемых временных интервалов kt в зависимости от длины исследуемого сигнала Nt, ширины оконной функции N и процента перекрытия p выражается следующей формулой [9]:
.
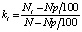Ширину оконной функции можно выбрать, зная минимальное разрешение по частоте df, частоту дискретизации Fs и нормированную ширину главного лепестка АЧХ оконной функции по нулевому уровню F0 [10]:
.
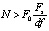Исходя из предположения, что частоты гармоник будут приблизительно кратны угловой скорости, а также основываясь на начальных данных, согласно которым угловая скорость в начале исследуемого процесса составит ≈ 3 рад/с, выберем максимальное значение минимального разрешения по частоте 0,7879 рад/с = 0,1254 Гц. В качестве оконной функции выберем окно Хэмминга с подавлением 42 дБ (F0 = 4), шириной 215 точек; перекрытие 75 %. Построим спектрограмму скорости рулона при тех же исходных параметрах (рис. 5); интенсивность цвета показывает амплитуду частотных составляющих.
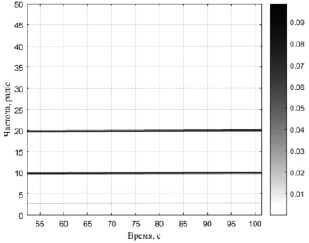
Рис. 5. Спектрограмма линейной скорости рулона
Как можно заметить, ОПФ выделяет две основные частоты: 10 и 20 рад/с , слабо изменяющиеся линейно.
Выводы
В данной статье было выполнено математическое моделирование рулона в узле размотки. Рассматривалось движение рулона под действием постоянной силы натяжения полотна материала в условиях отсутствия какого-либо тормозного элемента и при наличии электродвигателя постоянного тока, работающего в режиме противовключения. Как и ожидалось, отсутствие тормоза приводит к увеличению скорости рулона.
Применение электродвигателя как тормоза рулона привело к начальной стабилизации скорости рулона. Необходимо отметить, что получившаяся система классифицируется как система с разомкнутым управлением. Колебания скорости рулона, инициирующиеся самим рулоном, объясняются отсутствием обратной связи и основного алгоритма управления в системе.
Исследование получившихся результатов посредством оконного преобразования Фурье показало наличие двух основных гармоник с медленно изменяющимися частотами для выбранного интервала.
В дальнейшем полученные результаты будут использованы при моделировании узла размотки, всей перемоточной машины и синтезе алгоритма управления ей.
Библиографическая ссылка
Степанов П.Е., Усов А.Г. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УЗЛА РАЗМОТКИ РУЛОНА ТЕКСТИЛЬНЫХ И ПОЛИГРАФИЧЕСКИХ МАТЕРИАЛОВ // Современные наукоемкие технологии. – 2020. – № 12-2. – С. 317-323;URL: https://top-technologies.ru/ru/article/view?id=38449 (дата обращения: 07.09.2024).