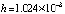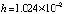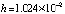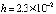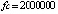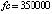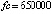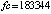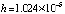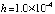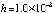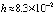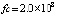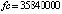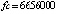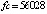Введение и постановка вопроса
В работе рассматривается кусочно-интерполяционное приближение функций одной вещественной переменной с помощью интерполяционных полиномов Лагранжа и Ньютона. Полиномы преобразуются к виду алгебраических полиномов с числовыми коэффициентами путем восстановления коэффициентов полинома по его корням. Применяются формулы, отличные от формул Виета [1] и не использующие уравнения Ньютона для симметрических функций корней [1, 2]. От конструируемого метода требуется инвариантность относительно вида функции и диапазона независимой переменной при условии достижения высокой точности приближения и одновременно малой временной сложности. На этой основе метод применяется для приближения производных и первообразных. Кусочно-полиномиальное приближение первообразной используется для построения квадратурных формул, представляющих собой аналог подхода Ньютона – Котеса [3]. Формулы реализованы аналитически и программно для произвольной степени полинома, интерполирующего подынтегральную функцию, что позволяет достигать сравнительно высокой точности вычисления интеграла. Приближенное решение задачи Коши для обыкновенных дифференциальных уравнений (ОДУ) строится на основе интерполяционных полиномов Лагранжа и Ньютона, аналогично преобразованных к виду алгебраических полиномов с числовыми коэффициентами. С помощью преобразованных полиномов приближаются правые части каждого уравнения системы ОДУ. Первообразная от полинома с соответственным значением константы – координата приближенного решения, подставляется в функцию правой части. Процесс итерационно повторяется, в результате решение приближается со сравнительно высокой точностью. Метод реализуется совместно с кусочной интерполяцией. Цель сообщения – представить математическое описание метода, его алгоритмизацию и программную реализацию. Анализируется вычислительная устойчивость, границы погрешности, временная сложность для нежестких и жестких задач. Дано сравнение с методами Рунге – Кутты, Батчера и Дормана – Принса [4, 5]. Отличительное качество предложенного метода состоит в ограниченном накоплении погрешности при сохранении приемлемой трудоемкости, что востребовано в задачах моделирования физических, химических процессов [5], в задачах планетной астрономии [6]. Описан численный эксперимент, исследуется возможность уменьшения погрешности без автоматического выбора параметров, изложенного в [7]. Вместе с упрощением метода требуется существенно снизить его трудоемкость.
Цель работы: раскрыть возможности применения алгоритма восстановления коэффициентов полинома по его корням для задач приближенного вычисления функций, производных и интегралов в рамках кусочной интерполяции. Требуется показать эффективность данного подхода для приближенного решения задачи Коши для обыкновенных дифференциальных уравнений. Основной аспект исследования заключается в достижении максимальной точности приближения, при этом указывается возможность минимизации трудоемкости метода. Цель включает математическое обоснование метода и экспериментальное подтверждение его эффективности в рассматриваемых аспектах. Для верификации достоверности приведены коды программ, использованных в численных экспериментах.
Инвариантное восстановление коэффициентов полинома по его корням. Приводимое непосредственно ниже преобразование является основой всех излагаемых в дальнейшем приложений. Пусть рассматривается полином 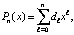 с коэффициентом dn = 1, и корнями
с коэффициентом dn = 1, и корнями 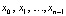 , так что
, так что
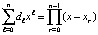 . (1)
. (1)
Если 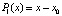 , то полагается
, то полагается 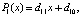 где
где 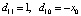 . Если уже вычислены коэффициенты полинома
. Если уже вычислены коэффициенты полинома 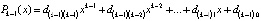 ,
, 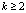 то
то 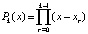 и
и 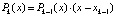 . Приравнивание коэффициентов при одинаковых степенях влечет
. Приравнивание коэффициентов при одинаковых степенях влечет
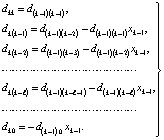 . (2)
. (2)
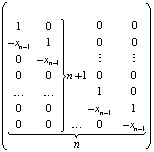
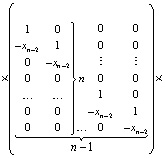
Здесь 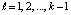 . При k = n левые части (2) совпадут с искомыми значениями коэффициентов полинома (1). Алгоритм сохраняется для комплексных корней и коэффициентов, программируется в виде двойного цикла [8]. В матричной форме (2) можно записать в виде
. При k = n левые части (2) совпадут с искомыми значениями коэффициентов полинома (1). Алгоритм сохраняется для комплексных корней и коэффициентов, программируется в виде двойного цикла [8]. В матричной форме (2) можно записать в виде
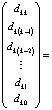
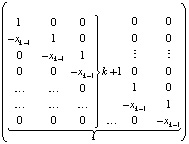
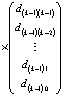 .
.
При k = n выражаются коэффициенты полинома через все его n корней:
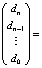
×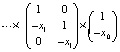 ,
,
или,
 ,
,
Соотношения (2) применяются для преобразования интерполяционных полиномов. Для интерполяции функции 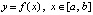 , полином Лагранжа можно записать в виде
, полином Лагранжа можно записать в виде
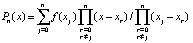 , (3)
, (3)
где xr – узлы интерполяции. Можно вычислить 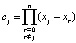 и
и 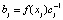 ,
, 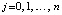 , тогда
, тогда 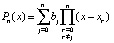 . Если при каждом
. Если при каждом 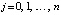 по схеме (2) найти коэффициенты полинома
по схеме (2) найти коэффициенты полинома 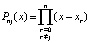 ,
, 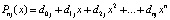 , то
, то 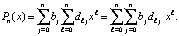 Отсюда
Отсюда 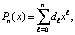 где
где 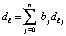 . Такое преобразование полинома Лагранжа инвариантно относительно степени полинома и вида функции, программируется в общем случае. Вместе с тем, на основании численного эксперимента, компьютерная реализация дает меньшую погрешность в случае равноотстоящих узлов.
. Такое преобразование полинома Лагранжа инвариантно относительно степени полинома и вида функции, программируется в общем случае. Вместе с тем, на основании численного эксперимента, компьютерная реализация дает меньшую погрешность в случае равноотстоящих узлов.
Преобразование полинома Лагранжа с равноотстоящими узлами интерполяции. Пусть на отрезке 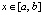 взяты равноотстоящие узлы для полинома (3):
взяты равноотстоящие узлы для полинома (3):
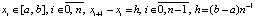 .
.
В этом случае 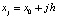 ,
, 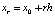 ,
, 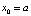 ,
, 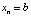 . Отсюда
. Отсюда 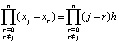 ,
, 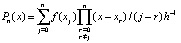 . Вводится переменная
. Вводится переменная 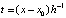 . Тогда
. Тогда 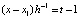 , …,
, …, 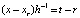 ,
, 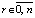 и
и
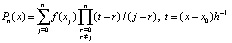 . (4)
. (4)
Аналогичное преобразование дано в [3]. Отличие составит перевод числителей из (4) в форму полиномов с целочисленными коэффициентами. В результате станет возможным аналитическое выражение первообразных, производных и организация итераций в правых частях ОДУ. Пусть числитель дроби 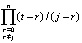 записан в виде
записан в виде
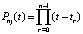 , (5)
, (5)
где роль корней полинома играют последовательные натуральные числа, среди которых пропускается j: 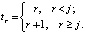 По схеме (2) получится
По схеме (2) получится
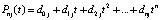 . (6)
. (6)
Коэффициенты полинома (6) будут целыми числами. Они могут быть априори вычислены и храниться в памяти компьютера как константы, не зависящие от интерполируемой функции, от диапазона и расположения её аргумента, причем это можно сделать для любого j и для всех степеней полинома n в априори заданных границах. Знаменатель в (4) отличается от числителя тем, что в нем t = j. В результате
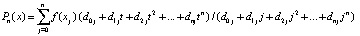 , (7)
, (7)
где 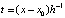 . Числитель и знаменатель в (7) удобно вычислять по схеме Горнера
. Числитель и знаменатель в (7) удобно вычислять по схеме Горнера
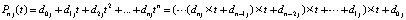 .
.
В этих обозначениях
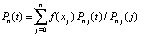 ,
, 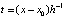 . (8)
. (8)
Если собрать коэффициенты при равных степенях слагаемых, то
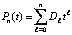 ,
, 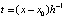 , (9)
, (9)
где Dℓ – результат приведения подобных. В дальнейшем приближение 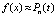 выполняется с использованием (8) и (9), что влечет две разновидности приближения производных:
выполняется с использованием (8) и (9), что влечет две разновидности приближения производных:
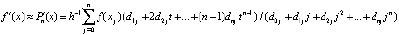 , (10)
, (10)
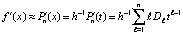 , (11)
, (11)
t из (9). На практике (10) несколько точнее (11).
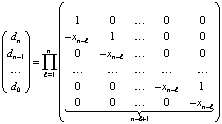
Кусочная интерполяция. Если (8)–(11) применяются на малых подынтервалах с общими границами разбиения
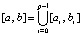 ,
, 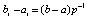 , (12)
, (12)
то точность приближения возрастет: функция и интеграл будут приближаться с точностью до 10–19–10–20, производная – с точностью 10–16–10–15 (Delphi, формат extended). Ниже предполагается, если не оговорено иное, что p = 2k, k – натуральное. Видоизменения (8), (9) формально совпадают между собой и с полиномом (3) при условии, что на одном и том же отрезке узлы одинаковы, одинаковы степени полиномов и интерполируется одна и та же функция. В этих же условиях все три полинома совпадают с интерполяционным полиномом Ньютона [3]. Для последнего в этом случае 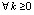 справедливо соотношение [7]:
справедливо соотношение [7]:
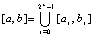 ,
, 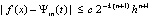
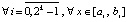 , (13)
, (13)
где предполагается, что f(x) определена и непрерывно дифференцируема на 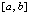 n + 1 раз. Здесь
n + 1 раз. Здесь 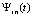 – интерполяционный полином Ньютона для интерполирования вперед на подынтервале
– интерполяционный полином Ньютона для интерполирования вперед на подынтервале 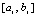 ,
, 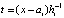 , hi – шаг интерполяции на
, hi – шаг интерполяции на 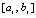 , h – шаг интерполяции полинома
, h – шаг интерполяции полинома 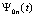 на
на 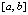 (при k = 0), поэтому
(при k = 0), поэтому 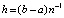 ,
, 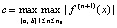 ,
, 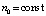 ,
, 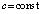 .
.
При каждом i из (13) рассматриваемый интерполяционный полином Ньютона имеет вид
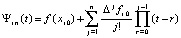 ,
, 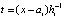 , (14)
, (14)
где узлы интерполяции 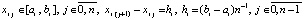 ,
, 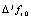 – конечная разность j-го порядка в узле
– конечная разность j-го порядка в узле 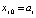 ,
, 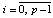 , p из (12),
, p из (12), 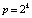 . Согласно (13) последовательность полиномов
. Согласно (13) последовательность полиномов 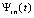 равномерно сходится к f(x) на
равномерно сходится к f(x) на 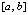 , если
, если 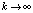 . Эти утверждения и (13) сохраняются для всех рассматриваемых видоизменений интерполяционных полиномов Лагранжа и Ньютона. В частности,
. Эти утверждения и (13) сохраняются для всех рассматриваемых видоизменений интерполяционных полиномов Лагранжа и Ньютона. В частности,
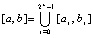 ,
, 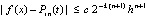
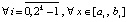 , (15)
, (15)
где 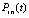 – полином Лагранжа вида (8), построенный на подынтервале
– полином Лагранжа вида (8), построенный на подынтервале 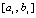 ,
, 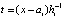 ,
, 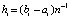 – шаг интерполяции на
– шаг интерполяции на 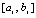 ,
, 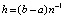 . В рассматриваемом случае
. В рассматриваемом случае
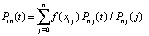 ,
, 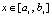 ,
, 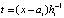 . (16)
. (16)
Аналогично, полином (8) на каждом подынтервале будет иметь вид
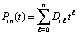 ,
, 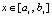 ,
, 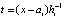 . (17)
. (17)
Полином Ньютона (14) на каждом подынтервале также можно преобразовать к виду алгебраического полинома с числовыми коэффициентами. Для этого каждый полином 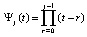 из (14) преобразуется в полином с целочисленными коэффициентами. Если положить
из (14) преобразуется в полином с целочисленными коэффициентами. Если положить 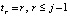 , по схеме (2) получится
, по схеме (2) получится
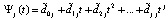 ,
,
где коэффициенты – целые числа. Почленное умножение таких полиномов на 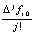 в (14) повлечет развернутую форму полинома Ньютона,
в (14) повлечет развернутую форму полинома Ньютона,
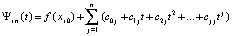 ,
, 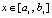 ,
, 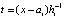 , (18)
, (18)
с вещественными коэффициентами. Если привести подобные в (18), то полином Ньютона примет вид
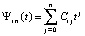 ,
, 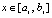 ,
, 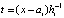 . (19)
. (19)
Программная реализация и результаты вычислений. Сопоставляется применение полиномов Лагранжа и Ньютона в рамках кусочной интерполяции.
Пример 1. На отрезке 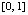 выполняется кусочная интерполяция функции
выполняется кусочная интерполяция функции 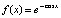 . Длина подынтервала
. Длина подынтервала 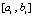 из (12) равна 0.00000001, в программной записи – hh=0.00000001. Абсолютная погрешность на выходе программы определяется как разность машинной реализации функции f:=exp(-cos(x)) и приближения полиномом Лагранжа на текущем подынтервале. Полином Лагранжа степени n = 2 в каждой проверочной точке сначала берется в форме (17), затем в форме (16). Такими парами выводятся результаты работы программы.
из (12) равна 0.00000001, в программной записи – hh=0.00000001. Абсолютная погрешность на выходе программы определяется как разность машинной реализации функции f:=exp(-cos(x)) и приближения полиномом Лагранжа на текущем подынтервале. Полином Лагранжа степени n = 2 в каждой проверочной точке сначала берется в форме (17), затем в форме (16). Такими парами выводятся результаты работы программы.
program LagVarSigmaCiklSvertka7777777;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25; hh=0.00000001; tt=10000000;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended; xx,dn: vec; z,d: vec0;
var n,i,j,k,l: integer; kk,rr: longint; a, aa, b, bb, h, h1, x, s, s1, sk, bj,t: extended;
function f (x: extended): extended;
begin f:=exp(-cos(x)); end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k :=2 to n do
begin
e[k,k]:=e[k-1,k-1]; for l :=1 to k-1 do e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1];
e[k,0]:=-e[k-1,0]*z[j,k-1];
end; for l:=n downto 0 do d[j,l]:= e[n,l];
end;
function gorner (var j:integer; var t: extended): extended;
var p:extended;
begin
p:=d[j,n]; for i:=n downto 1 do p:=p*t+d[j,i-1]; gorner:=p;
end;
function gorner1 (var j: integer): extended;
var pp:extended;
begin
pp:=d[j,n]; for i:=n downto 1 do pp:=pp*j+d[j,i-1]; gorner1:=pp;
end;
function gorner2 (var dn: vec; var t: extended): extended;
var p2:extended;
begin
p2:=dn[n]; for i:=n downto 1 do p2:=p2*t+dn[i-1]; gorner2:=p2;
end;
begin
aa:=0; bb:=1; kk:=0; rr:=0; a:=aa; b:=a+hh;
while b<=bb do
begin
n:=2; h:=(b-a)/n; h1:=h/3;
for j:=0 to n do xx[j]:=a+j*h; for j:=0 to n do for i:=0 to n-1 do
if i<j then z[j,i]:=i else z[j,i]:=i+1;
for j:=0 to n do ro( n, j, z,d);
for l:=0 to n do
begin sk:=0; for j:=0 to n do sk:=sk+f(xx[j])*d[j,l]/gorner1(j); dn[l]:=sk; end;
x:=a; while x <= b do
begin
t:=(x-xx[0])/h; s:=gorner2 (dn, t);
s1:=0; for j:=0 to n do s1:=s1+f(xx[j])*gorner(j,t)/gorner1(j);
kk:=kk+1; if kk=tt then
begin writeln; writeln (x,s,s-f(x)); writeln (x,s1,s1-f(x)); writeln; kk:=0; end;
x:=x+h1; end; rr:=rr+1; a:=aa+rr*hh;b:=a+hh; end; readln;
end.
Результат работы программы (в 1-й колонке – аргумент, во 2-й – интерполируемое значение функции, в 3-й – абсолютная погрешность кусочной интерполяции):
1.58896250000000E-0002 3.67925884259943E-0001 0.00000000000000E+0000
1.58896250000000E-0002 3.67925884259943E-0001 0.00000000000000E+0000
3.23696783333333E-0002 3.68072206146556E-0001-5.42101086242752E-0020
3.23696783333333E-0002 3.68072206146556E-0001 0.00000000000000E+0000
………………………………………………………………………………………
5.02012535000000E-0001 4.16188946037821E-0001-2.71050543121376E-0020
5.02012535000000E-0001 4.16188946037821E-0001 0.00000000000000E+0000
5.16298250000000E-0001 4.19097136869392E-0001 0.00000000000000E+0000
5.16298250000000E-0001 4.19097136869392E-0001 0.00000000000000E+0000
………………………………………………………………………………………
9.73441106666667E-0001 5.69806944079148E-0001 0.00000000000000E+0000
9.73441106666667E-0001 5.69806944079148E-0001-5.42101086242752E-0020
9.87726820000000E-0001 5.76610156860310E-0001 0.00000000000000E+0000
9.87726820000000E-0001 5.76610156860310E-0001 0.00000000000000E+0000
Таким образом, функция полиномами Лагранжа 2-й степени приближена с точностью 10–20.
Аналогичные результаты дает кусочная интерполяция по Ньютону. Пример взят для той же фукции со всеми теми же параметрами, но степень полинома выбрана n = 3. В реализации кусочной интерполяции полином Ньютона дает большую, чем полином Лагранжа, свободу в вариации степени полинома. Полином Ньютона степени n = 3 в каждой проверочной точке выводится сначала в форме (18), затем в форме (19).
program NewtVarSigmaSvertkaCikl99999KOEFF11;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended;
var xx,dn: vec; dm,dy,e,z,d:vec0; ,t,s,s1,s0,p,p1,a,b,h,h1,hh,aa,bb:extended;
i,j,k,k0,r,r1,l,l1,n: integer; kk,rr,tt: longint;
function f(x:extended):extended;
begin f:=exp(-cos(x)); end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k0 :=2 to n do
begin
e[k0,k0]:=e[k0-1,k0-1]; for l :=1 to k0-1 do
e[k0,k0-l]:=e[k0-1,k0-l-1]-e[k0-1,k0-l]*z[j,k0-1]; e[k0,0]:=-e[k0-1,0]*z[j,k0-1];
end;
for l:=n downto 0 do d[j,l]:= e[n,l];
end;
function gorner (var k:integer; var t: extended): extended;
var p:extended;
begin
p:=d[k,k]; for i:=k downto 1 do p:=p*t+d[k,i-1]; gorner:=p;
end;
function gorner1 (var k: integer): extended;
var pp:extended;
begin
pp:=d[k,k]; for i:=k downto 1 do pp:=pp*k+d[k,i-1]; gorner1:=pp;
end;
function gorner2 (var dn: vec; var t: extended): extended;
var p2:extended;
begin
p2:=dn[n]; for i:=n downto 1 do p2:=p2*t+dn[i-1]; gorner2:=p2;
end;
begin
aa:=0{-100}{+100}; bb:=1{-100}{+100}; tt:=10000000;
n:=3; a:=aa; hh:=0.00000001; b:=aa+hh; kk:=0; rr:=0; h:=(b-a)/n; h1:=h/3{33};
for k:=1 to n do for i:=0 to k-1 do z[k,i]:=i;
While b<=bb do
begin
for j:=0 to n do xx[j]:= a + j*h; for j:= 0 to n-1 do dy[1,j]:= f(xx[j+1])- f(xx[j]);
for k:=2 to n do for j:=0 to n-k do dy[k,j]:=dy[k-1,j+1]-dy[k-1,j];
x:=a; while x<= b do
begin
t:=(x-xx[0])/h; s:= f(xx[0]); dn[0]:=f(xx[0]);
for k:=1 to n do
begin for l:=1 to k do
begin ro(k, l, z,d); dm[k,l]:=dy[k,0]*d[k,l]/gorner1(k);
end; end;
for l:=1 to n do
begin s1:=0; for k:=1 to n do s1:=s1+dm[k,l]; dn[l]:=s1; end; s0:=gorner2 (dn,t);
for k:=1 to n do
begin ro(k, k, z,d); p:= gorner (k, t)/ gorner1 (k); s:=s+p*dy[k,0]
end; kk:=kk+1;
if kk=tt then begin writeln; writeln(x,' ',s,s-f(x)); writeln(x,' ',s0,s0-f(x));writeln;kk:=0; end;
x:=x+h1 end; rr:=rr+1; a:=aa+rr*hh;b:=aa+(rr+1)*hh; end; readln;
end.
Результат работы программы:
1.07471111111111E-0002 3.67900686691208E-0001 0.00000000000000E+0000
1.07471111111111E-0002 3.67900686691208E-0001 0.00000000000000E+0000
2.18193233333333E-0002 3.67967018670187E-0001 0.00000000000000E+0000
2.18193233333333E-0002 3.67967018670187E-0001 0.00000000000000E+0000
………………………………………………………………………………………
1.45657475555556E-0001 3.71795728758225E-0001 0.00000000000000E+0000
1.45657475555556E-0001 3.71795728758225E-0001-2.71050543121376E-0020
1.55657475555556E-0001 3.72354166892141E-0001 2.71050543121376E-0020
1.55657475555556E-0001 3.72354166892141E-0001 0.00000000000000E+0000
……………………………………………………………………………………….
9.85657475555556E-0001 5.75615636389719E-0001-5.42101086242752E-0020
9.85657475555556E-0001 5.75615636389719E-0001 0.00000000000000E+0000
9.95657475555556E-0001 5.80450177539984E-0001 5.42101086242752E-0020
9.95657475555556E-0001 5.80450177539984E-0001 5.42101086242752E-0020
В целом результаты аналогичны предыдущим. Следует подчеркнуть, что основной промежуток 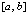 из (12) можно сдвигать на произвольную величину (в программе закомментирован сдвиг на ±100) с сохранением всех параметров программы и с той же границей погрешности. В этом специфика кусочной интерполяции: она не требует редукции аргумента к основному промежутку. Это относится и к интерполяции по Ньютону, и к интерполяции по Лагранжу.
из (12) можно сдвигать на произвольную величину (в программе закомментирован сдвиг на ±100) с сохранением всех параметров программы и с той же границей погрешности. В этом специфика кусочной интерполяции: она не требует редукции аргумента к основному промежутку. Это относится и к интерполяции по Ньютону, и к интерполяции по Лагранжу.
Пример 2. Обе программы из примера 1 преобразованы так, что по ним непосредственно вычисляются коэффициенты интерполяционного полинома в алгебраической форме, соответственные каждому подынтервалу. Это делается для произвольного сдвига исходного интервала, в программе, приводимой ниже, аргумент 35/37 сдвинут на 200. Обращение к памяти с соответственными подынтервалу коэффициентами выполняется по формулам 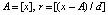 , где A – начало основного интервала, d – длина подынтервала, r – искомый индекс подынтервала. В программной реализации aa:=trunc(x); bb:=aa+1; r:=trunc((x-aa)/hh). Если сдвиг выполняется на отрицательное число, то в соответствии с определением оператора trunc формула обращения к подынтервалу несколько меняется, например x:=35/37-200; aa:=trunc(x)-1; bb:=aa+1; rr:=trunc((x-aa)/hh). Сдвиг допустим в границах диапазона, не нарушающего точность рассматриваемой целочисленной адресации.
, где A – начало основного интервала, d – длина подынтервала, r – искомый индекс подынтервала. В программной реализации aa:=trunc(x); bb:=aa+1; r:=trunc((x-aa)/hh). Если сдвиг выполняется на отрицательное число, то в соответствии с определением оператора trunc формула обращения к подынтервалу несколько меняется, например x:=35/37-200; aa:=trunc(x)-1; bb:=aa+1; rr:=trunc((x-aa)/hh). Сдвиг допустим в границах диапазона, не нарушающего точность рассматриваемой целочисленной адресации.
program LagVarSigmaSvertkaCiklAdr7777777Diapazon;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=12;{aa=0;bb=1;}hh=0.0000001; mm=10000000;
type vec=array[0..nn] of extended; vec0=array[0..nn,0..nn] of extended; vec00=array[0..nn,0..mm] of extended;
var n,i,j,k,l,r,{kk,}rr: longint; a,aa,b,bb, h, h1, x,x0, s,s1,sk, bj,t: extended;
xx,fk,tt,dn: vec; z,d: vec0; fkk:vec00;
function f (x: extended): extended;
begin f:= exp(-cos(x)) end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k :=2 to n do
begin
e[k,k]:=e[k-1,k-1]; for l :=1 to k-1 do
e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1]; e[k,0]:=-e[k-1,0]*z[j,k-1];
end;
for l:=n downto 0 do d[j,l]:= e[n,l];
end;
function gorner (var j:integer; var t: extended): extended;
var p:extended;
begin
p:=d[j,n]; for i:=n downto 1 do p:=p*t+d[j,i-1]; gorner:=p;
end;
function gorner1 (var j: integer): extended;
var pp:extended;
begin
pp:=d[j,n]; for i:=n downto 1 do pp:=pp*j+d[j,i-1]; gorner1:=pp;
end;
function gorner2 (var dn: vec; var t: extended): extended;
var p2:extended;
begin
p2:=dn[n]; for i:=n downto 1 do p2:=p2*t+dn[i-1]; gorner2:=p2;
end;
procedure koeff(var n:integer; var r:longint; var a,b:extended);
begin
h:=(b-a)/n; h1:=h/33;
for j:=0 to n do begin xx[j]:=a+j*h;fkk[j,r]:=f(xx[j]); end;
for j:=0 to n do for i:=0 to n-1 do if i<j then z[j,i]:=i else z[j,i]:=i+1;
for j:=0 to n do ro( n, j, z,d);
end;
begin
n:=2; x:=35/37+200; aa:=trunc(x);bb:=aa+1;rr:=trunc((x-aa)/hh); a:=aa+rr*hh;b:=a+hh;
koeff(n,rr, a,b); t:=(x-xx[0])/h; s:=0; for j:=0 to n do
s:=s+fkk[j,rr]*gorner(j,t)/gorner1(j); writeln;writeln;writeln;writeln;
writeln (' ','x=',x,' ','a=',a,' ');writeln; writeln (' ','function=',s,' ', 'pogrechnost=',s-f(x));
for j:=0 to n do ro( n, j, z,d); for l:=0 to n do
begin
sk:=0; for j:=0 to n do sk:=sk+f(xx[j])*d[j,l]/gorner1(j); dn[l]:=sk;
end;
s1:=gorner2 (dn, t); writeln;writeln;writeln;writeln; writeln (' ','x=',x,' ','a=',a,' ');writeln;
writeln (' ','function=',s1,' ', 'pogrechnost=',s1-f(x)); readln;
end.
Результат работы программы:
x= 2.00945945945946E+0002 a= 2.00945945900000E+0002
function= 3.70359395311641E-0001 pogrechnost= 2.71050543121376E-0020
x= 2.00945945945946E+0002 a= 2.00945945900000E+0002
function= 3.70359395311641E-0001 pogrechnost= 0.00000000000000E+0000
Аналогичная программа для полинома Ньютона имеет вид (сдвиг аргумента на -200 выполнен в отрицательную область)
program NewtonAdrPrav1111DiapzonOTRICAT;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=15; hh=0.000000009999; mm=10000009;
type vec=array[0..nn] of extended; vec0=array[0..nn,0..nn] of extended;
vec00=array[0..nn,0..mm] of extended;var xx,dn,fk,tt: vec; dm,dy: vec0; e,z,d:vec0; fkn:vec00;
aa,bb,x,x0,t,s,s1,sk,bj,s0,p1,a,b,h,h1:extended; i,j,k,k0,l,l1,n,r,r1,rr,kk:longint;
function f(x:extended):extended;
begin f:=exp(-cos(x)); end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k0 :=2 to n do
begin
e[k0,k0]:=e[k0-1,k0-1]; for l :=1 to k0-1 do
e[k0,k0-l]:=e[k0-1,k0-l-1]-e[k0-1,k0-l]*z[j,k0-1]; e[k0,0]:=-e[k0-1,0]*z[j,k0-1];
end;
for l:=n downto 0 do d[j,l]:= e[n,l];
end;
procedure koeffn(var n:integer; var r:longint; var a,b:extended);
begin
h:=(b-a)/n; for k:=1 to n do for i:=0 to k-1 do z[k,i]:=i;
for j:=0 to n do xx[j]:= a + j*h; fkn[0,r]:=f(xx[0]);
for j:= 0 to n-1 do dy[1,j]:= f(xx[j+1])- f(xx[j]); fkn[1,r]:= dy[1,0];
for k:=2 to n do for j:=0 to n-k do dy[k,j]:=dy[k-1,j+1]-dy[k-1,j]; fkn[k,r]:=dy[k,0];
for k:=1 to n do ro(k, k, z,d);
end;
function gorner (var k: longint; var t: extended): extended;
var p:extended;
begin
p:=d[k,k]; for i:=k downto 1 do p:=p*t+d[k,i-1]; gorner:=p;
end;
function gorner1 (var k: integer): extended;
var pp:extended;
begin
pp:=d[k,k]; for i:=k downto 1 do pp:=pp*k+d[k,i-1]; gorner1:=pp;
end;
begin
n:=3; x:=35/37-200;aa:=trunc(x)-1;bb:=aa+1; rr:=trunc((x-aa)/hh); a:=aa+rr*hh;b:=a+hh;
koeffn(n,rr, a,b); t:=(x-xx[0])/h; s:=fkn[0,rr];
for k:=1 to n do s:=s+fkn[k,rr]*gorner (k, t)/ gorner1 (k); writeln;writeln;writeln;writeln;
writeln (' ','x=',x,' ','a=',a,' ');writeln; writeln (' ','function=',s,' ', 'pogrechnost=',s-f(x)); readln;
end.
Результат работы программы:
x=-1.99054054054054E+0002 a=-1.99054054054055E+0002
function= 1.52698511574595E+0000 pogrechnost= 1.08420217248550E-0019
Пример 3. На основе полинома Лагранжа вычисляется кусочно-интерполяционное приближение производных по аналогам соотношений (10), (11). В программе, приводимой ниже, вычисляется производная функции 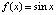 на
на 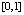 , степень полинома n = 6, длина подынтервала 0.035, полином взят в свернутой и развернутой форме. Программа примет вид
, степень полинома n = 6, длина подынтервала 0.035, полином взят в свернутой и развернутой форме. Программа примет вид
program LAGVarSigmaSvertkaPrPRAVCikl444444;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25;aa=0;bb=1;tt=100;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended; var n,i,j,k,l,kk,mm: integer;
a,b,h, h1, hh,x, s, s1, sk, bj, t, rr: extended; xx,dn,dpr: vec; z,d,dnpr: vec0;
function f (x: extended): extended;
begin f:=sin(x); end;
procedure ro(var mm, j:integer; var z:vec0;var d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k :=2 to mm do
begin
e[k,k]:=e[k-1,k-1]; for l :=1 to k-1 do e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1];
e[k,0]:=-e[k-1,0]*z[j,k-1];
end;
for l:=mm downto 0 do d[j,l]:= e[n,l];
end;
function gorner1 (var j: integer): extended;
var pp:extended;
begin
pp:=d[j,n]; for i:=n downto 1 do pp:=pp*j+d[j,i-1]; gorner1:=pp;
end;
function gorner2 (var n,j:integer; var dnpr:vec0; var t: extended): extended;
var pp1:extended;
begin
pp1:=dnpr[j,n-1]; for i:=n-1 downto 1 do pp1:=pp1*t+dnpr[j,i-1]; gorner2:=pp1;
end;
function gorner3 (var n:integer; var dpr:vec; var t: extended): extended;
var pp2:extended;
begin
pp2:=dpr[n-1]; for i:=n-1 downto 1 do pp2:=pp2*t+dpr[i-1]; gorner3:=pp2;
end;
begin
kk:= 0; mm:=20; n:=6; a:=aa; hh:=0.035; b:=aa+hh; rr:=0;
for j:=0 to mm do for i:=0 to mm-1 do if i<j then z[j,i]:=i else z[j,i]:=i+1;
while b<bb do
begin
h:=(b-a)/n; h1:=h/33; for j:=0 to n do begin xx[j]:=a+j*h; end;
for j:=0 to n do ro( n, j, z,d); for l:=0 to n do
begin
sk:=0; for j:=0 to n do sk:=sk+f(xx[j])*d[j,l]/gorner1(j); dn[l]:=sk;
end;
for j:=0 to n do
for l:=n downto 1 do dnpr[j,l-1]:=l*d[j,l]; for l:=n downto 1 do dpr[l-1]:=l*dn[l];
x:=a; while x <= b do
begin
t:=(x-xx[0])/h; s1:=gorner3 (n,dpr, t)/h; s:=0; for j:=0 to n do
s:=s+ (f(xx[j])*gorner2(n,j,dnpr,t)/gorner1(j)/h); kk:=kk+1;
if kk=tt then begin writeln; writeln (x,s1,s1-cos(x)); writeln (x,s,s-cos(x));writeln;kk:=0 end;
x:=x+h1;
end; rr:=rr+1; a:=aa+rr*hh;b:=aa+(rr+1)*hh;
end; readln
end.
Результат работы программы:
1.75000000000000E-0002 9.99846878907837E-0001-2.75387351811318E-0016
1.75000000000000E-0002 9.99846878907837E-0001-2.55166981294463E-0016
3.50000000000000E-0002 9.99387562523494E-0001 5.61622146358354E-0015
3.50000000000000E-0002 9.99387562523494E-0001 5.61492042097655E-0015
………………………………………………………………………………………
3.51590909090909E-0001 9.38826005066327E-0001 5.01118244122800E-0016
3.51590909090909E-0001 9.38826005066328E-0001 5.11906055739031E-0016
3.69267676767677E-0001 9.32591914962044E-0001 7.56176805200015E-0016
3.69267676767677E-0001 9.32591914962042E-0001-7.63820430516038E-0016
………………………………………………………………………………………
9.49595959595960E-0001 5.82011694704660E-0001-6.07695317678125E-0016
9.49595959595960E-0001 5.82011694704661E-0001-4.26254084112676E-0016
9.67272727272727E-0001 5.67547114328272E-0001 6.67483646479838E-0015
9.67272727272727E-0001 5.67547114328263E-0001-2.17599376017841E-0015
Производная приближена с точностью до 10–15.
Для развернутой формы (18) полинома Ньютона программа примет вид (вычисляется производная функции 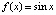 на
на 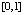 , степень полинома n = 9, длина подынтервала 0.035)
, степень полинома n = 9, длина подынтервала 0.035)
program NewtVarSigmaProizvCikl99999999999;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25; aa=0; bb=1;tt=100;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended;
var xx: vec; dn,dy,dnpr: vec0; e,z,d: vec0;
x,t,s,p,a,b,h,h1,hh: extended; i,j,k,k0,r,l,n: integer; kk,rr: longint;
function f(x:extended):extended;
begin f:=sin(x); end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k0 :=2 to n do
begin
e[k0,k0]:=e[k0-1,k0-1]; for l :=1 to k0-1 do
e[k0,k0-l]:=e[k0-1,k0-l-1]-e[k0-1,k0-l]*z[j,k0-1]; e[k0,0]:=-e[k0-1,0]*z[j,k0-1];
end;
for l:=n downto 0 do d[j,l]:= e[n,l];
end;
function gorner (var k:integer; var t: extended): extended;
var p:extended;
begin
p:=d[k,k]; for i:=k downto 1 do p:=p*t+d[k,i-1]; gorner:=p;
end;
function gorner1 (var k: integer): extended;
var pp:extended;
begin
pp:=d[k,k]; for i:=k downto 1 do pp:=pp*k+d[k,i-1]; gorner1:=pp;
end;
function gorner2 (var k:integer; var t: extended): extended;
var p:extended;
begin
p:=dnpr[k,k-1]; for i:=k-1 downto 1 do p:=p*t+dnpr[k,i-1]; gorner2:=p;
end;
begin
n:=9; a:=aa; hh:=0.01*3.5; b:=aa+hh; kk:=0; rr:=0; h:=(b-a)/n; h1:=h/333;
for k:=1 to n do for i:=0 to k-1 do z[k,i]:=i;
While b<=bb do
begin
for j:=0 to n do xx[j]:= a + j*h;
for j:= 0 to n-1 do dy[1,j]:= f(xx[j+1])- f(xx[j]);
for k:=2 to n do for j:=0 to n-k do dy[k,j]:=dy[k-1,j+1]-dy[k-1,j];
x:=a; while x<= b do
begin
t:=(x-xx[0])/h; s:= 0; for k:=1 to n-1 do
begin
ro(k, k, z,d); for l:=k downto 1 do dnpr[k,l-1]:=l*d[k,l];
p:= gorner2 (k, t)/gorner1(k)/h; s:=s+p*dy[k,0]
end;
kk:=kk+1; if kk=tt then begin writeln(x,' ',s,s-cos(x)); kk:=0;
end; x:=x+h1
end; rr:=rr+1; a:=aa+rr*hh;b:=aa+(rr+1)*hh;
end; readln;
end.
Результат работы программы:
1.15615615615615E-0003 9.99999331651546E-0001 2.16840434497101E-0019
2.32399065732399E-0003 9.99997299534928E-0001-1.08420217248550E-0018
………………………………………………………………………………………
4.45960960960961E-0001 9.02196595485431E-0001 4.87890977618477E-0019
4.47128795462129E-0001 9.01692264094780E-0001 1.02457105299880E-0017
………………………………………………………………………………………
9.78318318318318E-0001 5.58418390678033E-0001 7.02563007770607E-0017
9.79486152819486E-0001 5.57449221941874E-0001 1.15142270717961E-0016
Частичное улучшение предыдущего результата достигается вследствие повышения степени полинома Ньютона. В случае полинома Лагранжа это сделать не удается.
Приближенное вычисление интегралов. Непосредственно из (8), (9), (12) вытекают формулы приближенного вычисления интегралов. С разбиением (12)
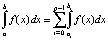 ,
, 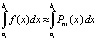 , (20)
, (20)
где 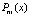 – полином (7), построенный на подынтервале
– полином (7), построенный на подынтервале 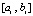 :
:
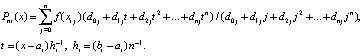
Отсюда
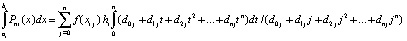 .
.
Интегрирование в правой части влечет
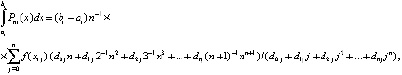 (21)
(21)
или
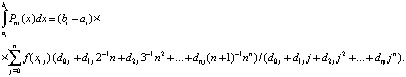
Сложение (21) по всем подынтервалам влечет
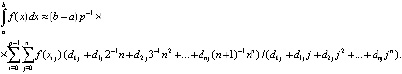 (22)
(22)
Если на каждом отрезке в правой части (20) подынтегральная функция 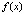 приближается с оценкой (15), где
приближается с оценкой (15), где 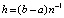 ,
, 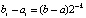 , то
, то
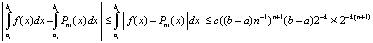 .
.
Отсюда
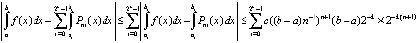 .
.
Окончательно
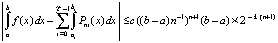 . (23)
. (23)
Оценка (23) верна в условиях, при которых выполняется (15). Если в этих условиях 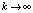 , то
, то 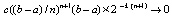 . Формулу (22) можно интерпретировать как разновидность формул Ньютона – Котеса [3]. Аналогичный подход реализуется и для полинома в форме (9). Однако предпочтительна именно форма (8) как основа получения (22): в (22) все коэффициенты dij имеют числовое значение, конструктивно вычисляемое для конкретного n на основе (2) из
. Формулу (22) можно интерпретировать как разновидность формул Ньютона – Котеса [3]. Аналогичный подход реализуется и для полинома в форме (9). Однако предпочтительна именно форма (8) как основа получения (22): в (22) все коэффициенты dij имеют числовое значение, конструктивно вычисляемое для конкретного n на основе (2) из 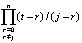 . Их значение не зависит от вида функции, интервала, подынтервала и т.д. Функцию, интервал и подынтервал идентифицируют только узловые значения
. Их значение не зависит от вида функции, интервала, подынтервала и т.д. Функцию, интервал и подынтервал идентифицируют только узловые значения 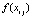 .
.
Аналогичное построение квадратурных формул на основе полинома Ньютона по тем же соображениям будет выполнено для развернутой формы полинома (18). Для этого в (20) 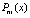 заменяется на
заменяется на 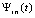 из (18). Получится
из (18). Получится
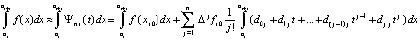 ,
,
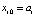 ,
, 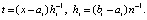 После замены переменной –
После замены переменной –
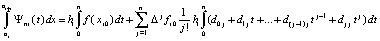 .
.
Взятие интегралов в правой части равенства влечет
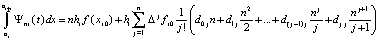 ,
,
или
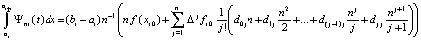 .
.
Отсюда
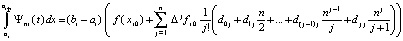 .
.
Сложение по всем подынтервалам влечет
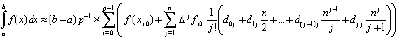 . (24)
. (24)
Поскольку для интерполяционного полинома Ньютона на каждом подынтервале имеет место оценка (13), то, аналогично (23), для приближения (24) справедлива оценка погрешности
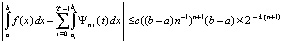 .
.
Программная реализация и примеры.
Пример 4. На основе полинома Лагранжа вычисляется кусочно-интерполяционное приближение интеграла от функции 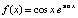 . Интеграл берется по отрезку
. Интеграл берется по отрезку 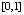 . Погрешность оценивается с использованием разности первообразной на концах отрезка. Степень полинома n = 5 на каждом подынтервале, длина подынтервала 0.00809.
. Погрешность оценивается с использованием разности первообразной на концах отрезка. Степень полинома n = 5 на каждом подынтервале, длина подынтервала 0.00809.
program LAGVarSigmaINTEGRAL55555;
{$APPTYPE CONSOLE}
uses SysUtils;
const nn=25; aa=0;bb=1;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended;
var n,i,j,k,l,mm,rr: longint; h, h1, x, s, sint, t, a, b, hh: extended; xx, tt: vec; z,d,dint: vec0;
function f (x: extended): extended;
begin {f:=cos(x);} f:=exp(sin(x))*cos(x); end;
procedure ro(var mm:integer; var j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k :=2 to mm do
begin
e[k,k]:=e[k-1,k-1]; for l :=1 to k-1 do
e[k,k-l]:=e[k-1,k-l-1]-e[k-1,k-l]*z[j,k-1]; e[k,0]:=-e[k-1,0]*z[j,k-1];
end;
for l:=mm downto 0 do d[j,l]:= e[mm,l];
end;
function gorner1 (var j: integer): extended;
var pp:extended;
begin
pp:=d[j,n]; for i:=n downto 1 do pp:=pp*j+d[j,i-1]; gorner1:=pp;
end;
function gorner0 (var j: integer; var n: integer): extended;
var pp0:extended;
begin
pp0:=dint[j,n+1]; for i:=n+1 downto 1 do pp0:=pp0*n+dint[j,i-1]; gorner0:=pp0;
end;
begin
mm:=20; rr:=0; hh:=0.00809; n:=5; sint:=0; a:=aa; b:=aa+hh;
for j:=0 to mm do for i:=0 to mm-1 do if i<j then z[j,i]:=i else z[j,i]:=i+1;
for j:=0 to n do ro( n, j, z,d); for j:=0 to n do for i:=0 to n do dint[j,i+1]:=d[j,i]/(i+1);
while b<=bb do
begin
x:=a; h:=(b-a)/n; for j:=0 to n do xx[j]:=a+j*h; t:=(x-xx[0])/h; s:=0; for j:=0 to n do
begin
s:=s+ h*f(xx[j])*gorner0(j,n)/gorner1(j);
end; sint:=sint+s; rr:=rr+1; a:=aa+rr*hh;b:=a+hh;
if (b < bb) and (b+hh > bb) then b:=bb;
end; writeln (b,sint,sint-(exp(sin(bb))-exp(sin(aa))){(sin(bb)-sin(aa))}); readln
end.
Результат работы программы (значение интеграла во 2-й колонке, абсолютная погрешность – в 3-й):
1.00316000000000E+0000 1.31977682471585E+0000 -1.08420217248550E-0019
Для функции 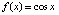 при тех же параметрах получится:
при тех же параметрах получится:
1.00316000000000E+0000 8.41470984807897E-0001 4.33680868994202E-0019
Пример 5. На основе полинома Ньютона вычисляется кусочно-интерполяционное приближение интеграла от функции 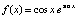 . Интеграл берется по отрезку
. Интеграл берется по отрезку 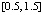 . Погрешность оценивается с использованием разности первообразной на концах отрезка. Степень полинома n = 13 на каждом подынтервале, длина подынтервала 0.2. Полином берется сначала в свернутой форме (19), затем в развернутой форме (18).
. Погрешность оценивается с использованием разности первообразной на концах отрезка. Степень полинома n = 13 на каждом подынтервале, длина подынтервала 0.2. Полином берется сначала в свернутой форме (19), затем в развернутой форме (18).
program NEWTONINTEGRALsigmasvertka55;
{$APPTYPE CONSOLE}
uses
SysUtils;
const nn=25; aa=0.5;bb=aa+1;
type vec=array[0..nn] of extended;vec0=array[0..nn,0..nn] of extended;var xx,dints: vec;
dy,e,z,d,dint:vec0; x,t,s,s1,s2,p,a,b,h,h1,hh,sint,sint1:extended;i,j,k,k0,k1,r,l,l1,n: integer; kk,tt,rr:longint;
function f(x:extended):extended;
begin {f:=cos(x);}f:=cos(x)*exp(sin(x)); end;
procedure ro(var n, j:integer; var z,d:vec0);
var e:vec0;
begin
e[1,1]:=1;e[1,0]:=-z[j,0]; for k0 :=2 to n do
begin
e[k0,k0]:=e[k0-1,k0-1]; for l :=1 to k0-1 do
e[k0,k0-l]:=e[k0-1,k0-l-1]-e[k0-1,k0-l]*z[j,k0-1]; e[k0,0]:=-e[k0-1,0]*z[j,k0-1];
end;
for l:=n downto 0 do d[j,l]:= e[n,l];
end;
function gorner1 (var k: integer): extended;
var pp:extended;
begin
pp:=d[k,k]; for i:=k downto 1 do pp:=pp*k+d[k,i-1]; gorner1:=pp;
end;
function gorner2 (var k: integer; var n:integer): extended;
var p2:extended;
begin
p2:=dint[k,k+1]; for i:=k+1 downto 1 do p2:=p2*n+dint[k,i-1]; gorner2:=p2;
end;
function gorner3 (var dints: vec; var n:integer): extended;
var p3:extended;
begin
p3:=dints[n+1]; for i:=n+1 downto 1 do p3:=p3*n+dints[i-1]; gorner3:=p3;
end;
begin
for k:=1 to nn do for i:=0 to k-1 do z[k,i]:=i; for k:=1 to nn do ro(k, k, z,d);
for k:=1 to nn-1 do for l:=0 to k do dint[k,l+1]:=d[k,l]/(l+1);
n:=13; hh:=(bb-aa)/5; kk:=0; tt:=1; rr:=0; a:=aa; b:=a+hh; s:=0; h:=(b-a)/n; sint:=0; sint1:=0;
while b<=bb do
begin
for j:=0 to n do xx[j]:= a + j*h; for j:= 0 to n-1 do dy[1,j]:= f(xx[j+1])- f(xx[j]);
for k:=2 to n do for j:=0 to n-k do dy[k,j]:=dy[k-1,j+1]-dy[k-1,j]; s:= f(xx[0])*h*n{(b-a)};
for k:=1 to n do
begin
p:= gorner2(k,n)/ gorner1 (k); s:=s+p*dy[k,0]*h;
end;
sint:=sint+s; dints[1]:=f(xx[0]); for l1:= 2 to n+1 do
begin
s1:=0; for k1:=1 to n do s1:=s1+dy[k1,0]*dint[k1,l1]/gorner1 (k1); dints[l1]:=s1;
end; s2:=gorner3 (dints, n)*h; sint1:=sint1+s2;
kk:=kk+1; rr:=rr+1; a:=aa+rr*hh; b:=a+hh;
if (b < bb) and (b+hh > bb) then b:=bb;
end; writeln;writeln;writeln;
writeln(b-hh,' ',sint,sint-{(sin(bb)-sin(aa))}(exp(sin(bb))-exp(sin(aa)))); writeln;writeln;
writeln(b-hh,' ',sint1,sint1-{(sin(bb)-sin(aa))}(exp(sin(bb))-exp(sin(aa)))); readln;
end.
Результат работы программы:
1.50000000000000E+0000 1.09633472124008E+0000 0.00000000000000E+0000
1.50000000000000E+0000 1.09633472124008E+0000 0.00000000000000E+0000
Для функции 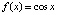 при тех же параметрах получится
при тех же параметрах получится
1.50000000000000E+0000 5.18069447999851E-0001 5.42101086242752E-0020
1.50000000000000E+0000 5.18069447999851E-0001 5.42101086242752E-0020
Кусочно-интерполяционное решение задачи Коши для ОДУ. Рассматривается задача Коши
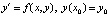 , (25)
, (25)
в области 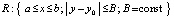 , где функция f(x, y) определена, непрерывно дифференцируема (в точках a – справа, b – слева) и удовлетворяет условию Липшица:
, где функция f(x, y) определена, непрерывно дифференцируема (в точках a – справа, b – слева) и удовлетворяет условию Липшица: 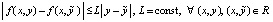 . Предполагается, что в R решение задачи (25) существует и единственно. Для простоты a, b те же, что в (12), и выполнено такое же разбиение на подынтервалы
. Предполагается, что в R решение задачи (25) существует и единственно. Для простоты a, b те же, что в (12), и выполнено такое же разбиение на подынтервалы 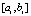 . Для интерполяции правой части (25) в f(x, y) подставляется приближенное значение y, вначале
. Для интерполяции правой части (25) в f(x, y) подставляется приближенное значение y, вначале 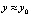 . Функция f(x, y0) приближается полиномами вида (16), (17) по изложенной выше схеме. При фиксированных n и k на отрезке
. Функция f(x, y0) приближается полиномами вида (16), (17) по изложенной выше схеме. При фиксированных n и k на отрезке 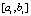 , i = 0, затем аналогично, при
, i = 0, затем аналогично, при 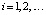 , выполняется итерационное уточнение, которое состоит в следующем. Пусть
, выполняется итерационное уточнение, которое состоит в следующем. Пусть 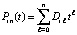 , тогда
, тогда 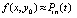 ,
, 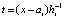 , hi – шаг интерполяции на
, hi – шаг интерполяции на 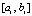 . Первообразная
. Первообразная 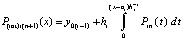 равная
равная 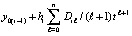 принимается за приближение решения:
принимается за приближение решения: 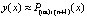 ,
, 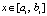 . Далее, полагается
. Далее, полагается 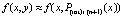 и при том же n, на том же отрезке строится интерполяционный полином вида (17) для приближения полученной функции:
и при том же n, на том же отрезке строится интерполяционный полином вида (17) для приближения полученной функции: 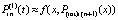 ,
, 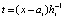 . От этого полинома снова берется первообразная с тем же значением константы
. От этого полинома снова берется первообразная с тем же значением константы 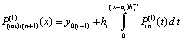 , подставляется в правую часть,
, подставляется в правую часть, 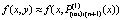 , которая затем интерполируется аналогично:
, которая затем интерполируется аналогично: 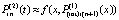 . Фактически итерации
. Фактически итерации 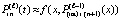 ,
, 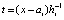 ,
, 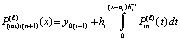 ,
, 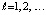 , продолжаются до заданной границы
, продолжаются до заданной границы 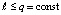 , абстрактно их количество не ограничивается. Выше за значение
, абстрактно их количество не ограничивается. Выше за значение 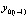 было принято
было принято 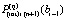 . По окончании итераций на
. По окончании итераций на 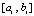 выполняется переход к
выполняется переход к 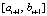 , где за значение
, где за значение 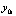 принимается
принимается 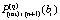 . Оценки погрешности будут выполняться ниже при дополнительных предположениях. Учитывая, что в случае равноотстоящих узлах на одном и том же отрезке, при интерполяции одной и той же функции интерполяционные полиномы Лагранжа и Ньютона одинаковой степени совпадают во всех рассмотренных формах, для упрощения обозначений предполагается, что интерполяция выполняется полиномом вида (3). Более точно, интерполяция предполагается без перехода к переменной t, при этом полином имеет полностью приведенные числовые коэффициенты:
. Оценки погрешности будут выполняться ниже при дополнительных предположениях. Учитывая, что в случае равноотстоящих узлах на одном и том же отрезке, при интерполяции одной и той же функции интерполяционные полиномы Лагранжа и Ньютона одинаковой степени совпадают во всех рассмотренных формах, для упрощения обозначений предполагается, что интерполяция выполняется полиномом вида (3). Более точно, интерполяция предполагается без перехода к переменной t, при этом полином имеет полностью приведенные числовые коэффициенты: 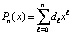 , на
, на 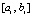 такой полином Лагранжа записывается в виде
такой полином Лагранжа записывается в виде
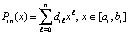 . (26)
. (26)
Погрешность интерполяции на 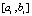 оценивается из (15), правая часть этой оценки обозначается
оценивается из (15), правая часть этой оценки обозначается 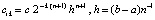 . Вначале рассматривается погрешность приближения решения с итерационным уточнением только на отрезке
. Вначале рассматривается погрешность приближения решения с итерационным уточнением только на отрезке 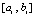 . При этом будет предполагаться, что решение на этом отрезке соответствует не начальным условиям из (25), а начальным условиям именно на этом отрезке:
. При этом будет предполагаться, что решение на этом отрезке соответствует не начальным условиям из (25), а начальным условиям именно на этом отрезке: 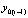 . В таком случае решение
. В таком случае решение 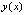 и приближение
и приближение 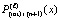 имеют одинаковые начальные значения на данном отрезке. Поэтому
имеют одинаковые начальные значения на данном отрезке. Поэтому 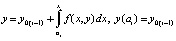 , вместе с тем
, вместе с тем 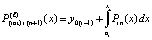 , где учитывается (26), так что не требуется замена переменной. Сначала оценки выполняются в предположении, что для некоторой последовательности номеров ℓ
, где учитывается (26), так что не требуется замена переменной. Сначала оценки выполняются в предположении, что для некоторой последовательности номеров ℓ
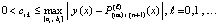 , (27)
, (27)
где 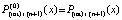 . С учетом одинаковых начальных значений абсолютная погрешность ℓ-й итерации примет вид
. С учетом одинаковых начальных значений абсолютная погрешность ℓ-й итерации примет вид 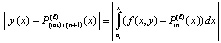 , отсюда
, отсюда
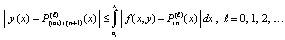 . (28)
. (28)
По построению 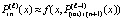 , погрешность интерполяции обозначается
, погрешность интерполяции обозначается 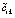 , в этом обозначении
, в этом обозначении 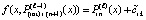 . Подстановка в (28) влечет
. Подстановка в (28) влечет
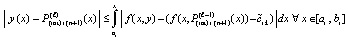 .
.
Согласно (15) 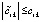 , поэтому
, поэтому
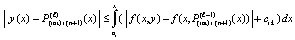 . (29)
. (29)
Отсюда, при условии, что для индекса 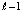 верно (27), следует неравенство
верно (27), следует неравенство
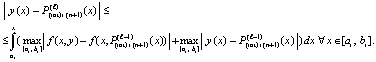
С применением условия Липшица
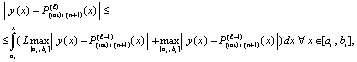 (30)
(30)
или
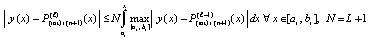 .
.
Очевидно,
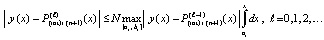 ,
,
или
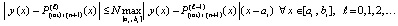 .
.
Ввиду произвольности 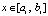 в обеих частях неравенства можно перейти к максимуму:
в обеих частях неравенства можно перейти к максимуму:
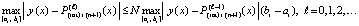 (31)
(31)
Пусть левая часть неравенства (31) обозначена 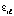 , в этом обозначении
, в этом обозначении
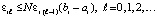 . (32)
. (32)
В (32) 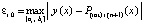 и
и 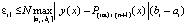 . Согласно построению
. Согласно построению 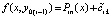 , поэтому, с учетом (28) при ℓ = 0 и проделанных выше преобразований,
, поэтому, с учетом (28) при ℓ = 0 и проделанных выше преобразований,
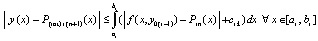 .
.
Отсюда 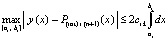 , где
, где 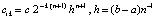 , или
, или
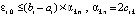 . (33)
. (33)
Из (32), (33) 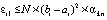 , поэтому
, поэтому 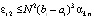 . По индукции
. По индукции
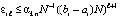 . (34)
. (34)
Неравенство (34) является следствием (31) и верно для тех последовательных 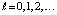 , для которых не нарушено (27). Не умаляя общности, можно предположить, что
, для которых не нарушено (27). Не умаляя общности, можно предположить, что 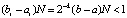 , тогда в (34)
, тогда в (34) 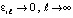 . Поэтому неравенство (27) при некотором ℓ необходимо окажется нарушенным, нарушение означает, что
. Поэтому неравенство (27) при некотором ℓ необходимо окажется нарушенным, нарушение означает, что
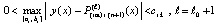 . (35)
. (35)
Пусть 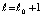 будет первым элементом последовательности
будет первым элементом последовательности 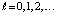 , при котором неравенство (27) будет нарушено и выполнится (35). В этом случае для номера
, при котором неравенство (27) будет нарушено и выполнится (35). В этом случае для номера 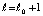 еще сохраняются (31) и (34). Из (29) с применением условия Липшица следует
еще сохраняются (31) и (34). Из (29) с применением условия Липшица следует
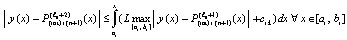 . (36)
. (36)
Отсюда, с учетом выполнения (34) для 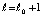 и того, что
и того, что
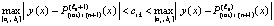 ,
,
подынтегральное выражение в (36) можно заменить соответственным выражением из (30):
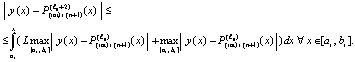 (37)
(37)
Но для правой части (37), после перехода к максимуму в обеих частях неравенства, сохраняется оценка (34), при которой левая часть неравенства (34) уже нарушает (36) и не превосходит cik. Поэтому и левая часть (37) не превзойдет cik:
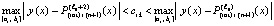 . (38)
. (38)
Аналогично
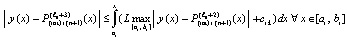 , (39)
, (39)
и
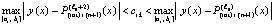 ,
,
поэтому подынтегральное выражение в правой части (39) можно заменить на выражение из (30), что повлечет совпадение с правой частью (37):
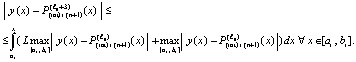
Повторение предыдущих рассуждений влечет
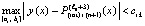 . (40)
. (40)
В силу очевидной индукции неравенства (38) и (40) перейдут в неравенство
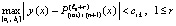 .
.
Из изложенного вытекает
Лемма 1. Пусть в рассматриваемых условиях, в числе которых условия выполнения (13), (15) применительно к правой части (25), а также условие (27) и предположение 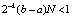 , выполняется кусочная интерполяция с итерационным уточнением решения задачи (25). Тогда на произвольном отрезке
, выполняется кусочная интерполяция с итерационным уточнением решения задачи (25). Тогда на произвольном отрезке 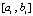 из (12) найдется номер r0, такой, что итерационное уточнение будет удовлетворять неравенству
из (12) найдется номер r0, такой, что итерационное уточнение будет удовлетворять неравенству
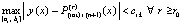 . (41)
. (41)
Для номеров из (41) сохраняется (29), откуда с применением условия Липшица
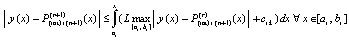 .
.
Из (41) 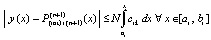 , или,
, или,
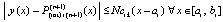 .
.
Следовательно, 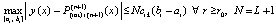 , или
, или
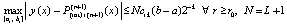 . (42)
. (42)
Теорема 1. В условиях леммы 1 абсолютная погрешность решения задачи (25) оценивается из (42). Согласно (42) погрешность кусочной интерполяции на отдельном подынтервале уменьшается за счет итерационного уточнения пропорционально 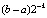 .
.
Следствие 1. В тех же условиях скорость сходимости к (42) определяется геометрической прогрессией из (34).
Следствие 2. В условиях теоремы 1 абсолютная погрешность решения задачи (25) на всем отрезке (12) оценивается из соотношения 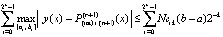 , или
, или
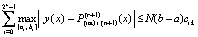 . (43)
. (43)
Согласно (43) итерационное уточнение позволяет, с точностью до постоянного множителя 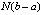 , приближать решение на всем отрезке (12) с абсолютной погрешностью кусочной интерполяции на одном подынтервале из (12). Подстановка в (43) cik из (15) влечет
, приближать решение на всем отрезке (12) с абсолютной погрешностью кусочной интерполяции на одном подынтервале из (12). Подстановка в (43) cik из (15) влечет
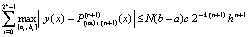 ,
,
или
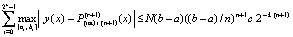 . (44)
. (44)
Пусть задано 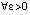 . В (44) можно указать такое
. В (44) можно указать такое 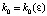 , что правая часть не превзойдет ε при
, что правая часть не превзойдет ε при 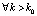 . Именно,
. Именно, 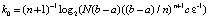 .
.
Теорема 2. В условиях леммы 1 абсолютная погрешность решения задачи (25) на всем отрезке решения из (12) оценивается из (44). При этом 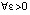 верно соотношение
верно соотношение
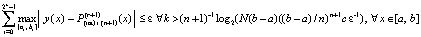 ,
,
означающее равномерную сходимость метода, если 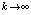 .
.
Изложенные рассуждения и оценки переносятся на случай интерполяционного полинома Ньютона, взятого в форме (18) или (19), с точностью до замены обозначений 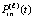 на
на 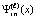 , и
, и 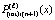 на
на 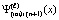 .
.
Теорема и следствия дают формальную оценку погрешности в абстрактных условиях, включающих существование n + 1 производной у функции правой части (25). Однако сама по себе интерполяция возможна в самых широких условиях, поэтому метод всегда можно применять в условиях существования и единственности. На практике многое определяется не только малостью подынтервала в (44), но видом правой части (25), устойчивостью решения в смысле Ляпунова, жесткостью или нежесткостью класса задач. Тем не менее во всех таких экспериментально рассмотренных случаях предложенный метод обладает меньшей погрешностью, чем известные методы, отличаясь фиксированной границей накопления погрешности на большом промежутке решения.
Численный эксперимент. Часть эксперимента дана на примерах задач, имеющих аналитические решения. Обсуждаются также результаты моделирования химических процессов и задач небесной механики. Эксперимент проводился с помощью ПК на базе процессора Intel(R) Core(TM) i5-2500. Ниже представлены результаты на основе интерполяции по Ньютону. Использование полинома Лагранжа дает практически такие же результаты.
Пример 1. Задача 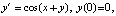 имеет решение
имеет решение 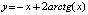 . Абсолютная погрешность приближения на
. Абсолютная погрешность приближения на 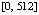 разностными и предложенным кусочно-интерполяционным (PP) методами дана в табл. 1 с числом обращений (fc) к правой части.
разностными и предложенным кусочно-интерполяционным (PP) методами дана в табл. 1 с числом обращений (fc) к правой части.
Таблица 1
Погрешность и число обращений к правой части при решении задачи примера 1
|
x |
Runge-Kutt_4 |
Butcher_6 |
Dorman-Prince_8 |
PP |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.12 10.24 … 256.00 261.12 … 506.88 512.00 |
1.315Е-0015 3.422E-0016 … 3.608E-0016 8.327E-0016 … 3.053E-0016 8.049E-0016 |
2.665E-0016 6.765E-0017 … 2.498E-0016 4.441E-0016 … 1.749E-0015 2.137E-0015 |
1.518E-0018 7.373E-0018 … 7.078E-0016 8.882E-0016 … 4.524E-0015 3.747E-0015 |
1.084E-0018 0.000E+0000 … 4.163E-0017 5.551E-0017 … 2.776E-0017 5.551E-0017 |
Граница погрешности 10–15 соответствует методам 4-го (Runge-Kutt_4) , 6-го (Butcher_6) и 8-го (Dorman-Prince_8) порядков. Величины шагов для каждого разностного метода выбраны с целью наименьшей погрешности. Методу Батчера соответствует количество обращений к функции правой части fc = 350000. Кусочно-интерполяционное решение с параметрами 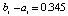 , n = 15, ℓ = 13 характеризуется порядком погрешности 10–17 при
, n = 15, ℓ = 13 характеризуется порядком погрешности 10–17 при 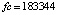 .
.
Программа предложенного решения данной задачи имеет вид
program RD_example_1;
{$APPTYPE CONSOLE}
uses SysUtils, Math;
var koutput,kiter:integer; Npol:byte; fc:longint;
Anach,Bkonech,velint,ynach,hpd_:extended;
function f(x,y: extended):extended;
begin f:=cos(x+y);fc:=fc+1; end;
function fun(x:extended):extended;
begin fun:=-x+2*arctan(x) end;
procedure RD(y_nach,A_nach,B_konech,vel_int:extended;n:byte;hpd:extended;k_iter,k_output:integer);
const nn=20;
type matr=array[0..nn,0..nn] of extended; vect=array[0..nn] of extended;
matrC=array[-4..nn+1] of extended; matrAll=array[0..33000] of matrC; matrC_=^matrAll;
var d:matr; a0,b0,x,y0:extended; i:integer; Ck1:matrC_; pod:longint ;
procedure Viet(n:byte; var d:matr);
var k,i:byte; e:matr;
begin e[1,1]:=1; e[1,0]:=0; for k:=2 to n do begin e[k,0]:=-e[k-1,0]*(k-1);
for i:=1 to k-1 do e[k,k-i]:=e[k-1,k-i-1]-e[k-1,k-i]*(k-1); e[k,k]:=e[k-1,k-1] end;
for k:=1 to n do for i:=0 to k do d[i,k]:=e[k,i] end;
procedure Konech_Raznoct(fy:vect; n:byte; var dy:matr);
var i,j:byte;
begin for j:=0 to n-1 do dy[1,j]:=fy[j+1]-fy[j];
for i:=2 to n do for j:=0 to n-i do dy[i,j]:=dy[i-1,j+1]-dy[i-1,j] end;
procedure Newton(U:Vect; n:byte; var Mcoef:matrC);
var dy:matr; b:vect; p,s:extended; j,i:byte;
begin Konech_Raznoct(U,n,dy); p:=1;
for j:=1 to n do begin p:=p*j; b[j]:=dy[j,0]/p; end; Mcoef[0]:=U[0];
for i:=1 to n do begin s:=0; for j:=i to n do s:=s+d[i,j]*b[j]; Mcoef[i]:=s; end end;
function Gorner(Mcoef:matrC; x:extended):extended;
var i,n:byte; s,t:extended;
begin t:=(x-Mcoef[-1])/Mcoef[-2]; n:=trunc(Mcoef[-3]); s:=Mcoef[n];
for i:=n-1 downto 0 do s:=t*s+Mcoef[i]; Gorner:=s end;
procedure Polynomial(x:vect; h,y0:extended; n,K_it:integer; var C:matrC);
var i,iter:integer; fy,y,ytemp:vect; A:matrC; sum:extended;
begin for i:=0 to n do y[i]:=y0; for iter:=1 to K_it do
begin for i:=1 to n do ytemp[i]:=y[i]; for i:=0 to n do fy[i]:=f(x[i],y[i]);
Newton(fy,n,A); C[0]:=y[0]; C[-1]:=x[0]; C[-2]:=h; C[-3]:=n+1;C[-4]:=n*h;
for i:=1 to n+1 do C[i]:=A[i-1]*h/i; for i:=1 to n do y[i]:=Gorner(C,x[i]);
sum:=0; for i:=1 to n do sum:=sum+abs(y[i]-ytemp[i]);
if (sum<1e-40) then break; if (sum>=1e50) then break; end end;
procedure Subinterval(hpd:extended;n,K_it:integer; a0,b0,Ynach:extended; var Ck:matrC_);
var a00,b00,y0,h:extended; m,pod:longint; x:vect; j:byte;
begin a00:=a0;b00:=a00+hpd; y0:=Ynach;x[0]:=a0;m:=0; pod:=0;
while a00<=b0-hpd/10 do begin h:=(b00-a00)/n; for j:=1 to n do begin inc(m); x[j]:=a0+m*h end;
Polynomial(x,h,y0,n,K_it,Ck^[pod]); y0:=gorner(Ck^[pod],x[n]);
x[0]:=x[n];inc(pod); a00:=a00+hpd; b00:=a00+hpd end end;
begin
fc:=0; New(Ck1); Viet(nn,d); writeln('x':4,'y':15,'Pogr':25); writeln;
a0:=A_nach; b0:=a0+vel_int; y0:=y_nach;
while a0 <= B_konech-vel_int/2 do begin Subinterval(hpd,n,k_iter,a0,b0,y0,Ck1); writeln;
for i:=1 to k_output-1 do begin x:= a0+i*Vel_int/k_output; pod:=trunc((x-a0)/Ck1^[0,-4]);
if x>Bkonech then break;
writeln(x:7:3,' ', Gorner(Ck1^[pod],x), ' ',abs(Gorner(Ck1^[pod],x)-fun(x))); end;
if abs(frac((b0-a0)/Ck1^[0,-4]))<1e-18 then pod:=trunc((b0-a0)/Ck1^[0,-4])-1
else pod:=trunc((b0-a0)/Ck1^[0,-4])-1;
y0:=Gorner(Ck1^[pod],b0); writeln(b0:7:3,' ', y0, ' ',abs(y0-fun(b0)));
a0:=a0+vel_int; b0:=a0+vel_int; end; Dispose(Ck1); end;
begin
Anach:=0; Bkonech:=512; ynach:=0; velint:=512; Npol:=15; hpd_:=0.345; kiter:=13; koutput:=100;
RD(ynach,Anach,Bkonech,velint,Npol,hpd_,kiter,koutput); writeln(fc); readln; end.
Пример 2. Система 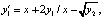
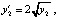 при
при 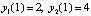 имеет решение
имеет решение 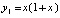 ,
, 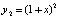 . Канонические нормы вектора абсолютных погрешностей компонент на отрезке
. Канонические нормы вектора абсолютных погрешностей компонент на отрезке 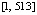 представлены в табл. 2 наряду с fc.
представлены в табл. 2 наряду с fc.
Таблица 2
Погрешность и число обращений к правой части при решении задачи примера 2
|
x |
Runge-Kutt_4 |
Butcher_6 |
Dorman-Prince_8 |
PP |
|
|
|
|
|
|
|
|
|
|
|
|
|
6.12 11.24 … 257.00 262.12 … 507.88 513.00 |
2.082E-0017 1.110E-0016 … 5.684E-0014 5.684E-0014 … 1.563E-0013 1.421E-0013 |
3.539E-0016 1.388E-0016 … 2.842E-0014 4.974E-0014 … 1.705E-0013 4.832E-0013 |
8.674E-0017 3.608E-0016 … 6.821E-0013 3.837E-0013 … 2.416E-0013 4.263E-0013 |
0.000E+0000 0.000E+0000 … 0.000E+0000 0.000E+0000 … 0.000E+0000 0.000E+0000 |
При одинаковом порядке погрешности среди разностных методов значением fc = 6656000 характеризуется метод Дормана – Принса. Кусочно-интерполяционное приближение с параметрами: 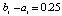 , n = 3, ℓ = 20, в большинстве проверочных точек дает значения «нулевых» погрешностей в формате вывода данных (extended), при увеличении числа проверочных точек встречаются значения 10–18–10–16. При этом
, n = 3, ℓ = 20, в большинстве проверочных точек дает значения «нулевых» погрешностей в формате вывода данных (extended), при увеличении числа проверочных точек встречаются значения 10–18–10–16. При этом 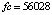 .
.
Пример 3. В [4] на серии тестовых задач представлено сравнение вычислительных качеств наиболее эффективных методов высокоточного решения нежестких задач Коши. Типичные результаты дает тестовая задача двух тел:
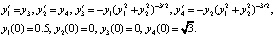 (45)
(45)
На 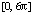 метод Дормана – Принса 8-го порядка дает решение задачи (45) с погрешностью порядка 10–14 при
метод Дормана – Принса 8-го порядка дает решение задачи (45) с погрешностью порядка 10–14 при 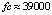 , экстраполяционная программа ODEX на том же отрезке достигает погрешности порядка 10–13 при
, экстраполяционная программа ODEX на том же отрезке достигает погрешности порядка 10–13 при 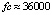 [4]. Наименьшей границы погрешности, порядка 10–16, на том же отрезке, среди исследованных методов численного приближения достигает интегратор Гаусса – Эверхарта 19-го порядка – GAUSS_32 [9], реализованный в среде Delphi. Метод адаптирован для решения задач небесной механики, в частности механизм выбора величины шага интегрирования осуществлен с учетом специфики плоской задачи двух тел [8]. Кусочно-интерполяционное решение задачи (45) характеризуется границей погрешности порядка 10–17 при
[4]. Наименьшей границы погрешности, порядка 10–16, на том же отрезке, среди исследованных методов численного приближения достигает интегратор Гаусса – Эверхарта 19-го порядка – GAUSS_32 [9], реализованный в среде Delphi. Метод адаптирован для решения задач небесной механики, в частности механизм выбора величины шага интегрирования осуществлен с учетом специфики плоской задачи двух тел [8]. Кусочно-интерполяционное решение задачи (45) характеризуется границей погрешности порядка 10–17 при 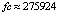 (параметры метода:
(параметры метода: 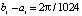 , n = 10, ℓ = 20). Аналогичные результаты получаются при решении других нежестких задач.
, n = 10, ℓ = 20). Аналогичные результаты получаются при решении других нежестких задач.
Пример 4. Периодическая реакция Белоусова – Жаботинского моделируется жесткой системой [5]:
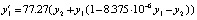 ,
,
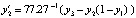 ,
,
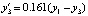 .
.
Результаты кусочно-интерполяционного приближения решения для начальных данных 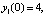
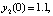
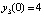 на отрезке
на отрезке 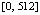 при вариации степени интерполяционного полинома и количества подынтервалов разбиения представлены в [7]. Фиксирование параметров метода и исключение дополнительных уточняющих процедур программы позволило сократить время решения задачи с границей погрешности 10–14 с
при вариации степени интерполяционного полинома и количества подынтервалов разбиения представлены в [7]. Фиксирование параметров метода и исключение дополнительных уточняющих процедур программы позволило сократить время решения задачи с границей погрешности 10–14 с 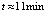 до
до 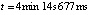 (
(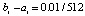 , n = 4, ℓ = 5).
, n = 4, ℓ = 5).
Замечание о наилучшем приближении. Если под этим понимать достижение заданной границы абсолютной погрешности ε с наименьшим количеством подынтервалов 2k при наименьшей (одной и той же) степени полинома n на каждом из подынтервалов, то в случае приближения функций можно воспользоваться элементарным алгоритмом из [10]. Его реализация сводится к циклическому увеличению n при наименьшем k в заданных пределах 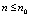 . По достижении предела n переходит в начальное значение, а k увеличивается на единицу,
. По достижении предела n переходит в начальное значение, а k увеличивается на единицу, 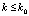 . На каждом шаге цикла выполняется сравнение на наборе проверочных точек функции и интерполирующего ее полинома. Если погрешность в проверочной точке не превосходит ε, продолжается проверка, иначе n переходит в начальное значение, а k увеличивается на единицу. Наименьшие n и k, при которых погрешность не превосходит ε во всех проверочных точках, принимаются за решение задачи. Если так приближать подынтегральную функцию, то это приводит к наилучшему приближению интеграла. Для часто повторяющихся функций, в частности библиотеки стандартных программ, коэффициенты интерполирующего полинома в алгебраической форме, например, (17) записываются в память для каждого подынтервала. В дальнейшем обращение к памяти выполняется по соотношениям
. На каждом шаге цикла выполняется сравнение на наборе проверочных точек функции и интерполирующего ее полинома. Если погрешность в проверочной точке не превосходит ε, продолжается проверка, иначе n переходит в начальное значение, а k увеличивается на единицу. Наименьшие n и k, при которых погрешность не превосходит ε во всех проверочных точках, принимаются за решение задачи. Если так приближать подынтегральную функцию, то это приводит к наилучшему приближению интеграла. Для часто повторяющихся функций, в частности библиотеки стандартных программ, коэффициенты интерполирующего полинома в алгебраической форме, например, (17) записываются в память для каждого подынтервала. В дальнейшем обращение к памяти выполняется по соотношениям 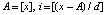 , где A – начало основного интервала, d – длина подынтервала, i – искомый индекс подынтервала и математический адрес соответственных коэффициентов. Временная сложность вычисления функции составит
, где A – начало основного интервала, d – длина подынтервала, i – искомый индекс подынтервала и математический адрес соответственных коэффициентов. Временная сложность вычисления функции составит 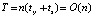 , где n – степень полинома,
, где n – степень полинома, 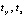 – время бинарного умножения и сложения. Так,
– время бинарного умножения и сложения. Так, 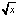 или xα, где α – иррациональное, могут быть вычислены за время двух умножений со сложением с отмеченной в примерах точностью. Высокая точность нужна хотя бы затем, чтобы в дальнейших преобразованиях накопление погрешности было ниже, чем при невысокой начальной точности приближения функции. Требуемая начальная точность не всегда может быть достигнута предложенным способом, если интерполируемая функция вычисляется из сложного выражения, как, например, функция Бесселя. В случае решения задачи Коши для ОДУ ставится другой вопрос: при каких n и k достигается наибольшая точность приближенного решения? Инвариантное решение возможно на основе вспомогательной функции, являющейся усложненным аналогом невязки, и специального набора контрольных точек. В деталях метод изложен в [7]. В представленной выше работе эти задачи не решались. Исследовались возможности достижения предельной для языка программирования точности приближения искомых функций на основе эвристического подбора параметров n и k. Нетрудно видеть, что такие возможности не представлялись бы, если бы в основе подхода не лежал перевод интерполяционного полинома в форму алгебраического полинома с числовыми коэффициентами при помощи алгоритма (2).
или xα, где α – иррациональное, могут быть вычислены за время двух умножений со сложением с отмеченной в примерах точностью. Высокая точность нужна хотя бы затем, чтобы в дальнейших преобразованиях накопление погрешности было ниже, чем при невысокой начальной точности приближения функции. Требуемая начальная точность не всегда может быть достигнута предложенным способом, если интерполируемая функция вычисляется из сложного выражения, как, например, функция Бесселя. В случае решения задачи Коши для ОДУ ставится другой вопрос: при каких n и k достигается наибольшая точность приближенного решения? Инвариантное решение возможно на основе вспомогательной функции, являющейся усложненным аналогом невязки, и специального набора контрольных точек. В деталях метод изложен в [7]. В представленной выше работе эти задачи не решались. Исследовались возможности достижения предельной для языка программирования точности приближения искомых функций на основе эвристического подбора параметров n и k. Нетрудно видеть, что такие возможности не представлялись бы, если бы в основе подхода не лежал перевод интерполяционного полинома в форму алгебраического полинома с числовыми коэффициентами при помощи алгоритма (2).
Необходимо отметить, что в случае решения задачи Коши для ОДУ эвристический подбор параметров n и k позволяет получить решение с существенно меньшей трудоемкостью, чем при автоматическом выборе этих параметров [7], причем без потери точности приближения, как отражено в примерах 1–4 и в табл. 1, 2. Показать эту возможность было одной из целей данной работы.
Объяснение сравнительно высокой точности предложенного метода заключается в следующем. Интерполяционные полиномы переводятся в форму алгебраических полиномов с числовыми коэффициентами на основе целочисленных преобразований их основных компонентов, как, например, в (3)–(9). Эти компоненты становятся полиномами с целыми коэффициентами. Для компьютерной арифметики с плавающей точкой целочисленные операции наименее подвержены накоплению погрешности. Кроме того, переход к приближению функций на подынтервалах дает возможность минимизировать модуль остаточного члена интерполяции. Для полинома Лагранжа (3) оценка погрешности на подынтервале примет вид [3]:
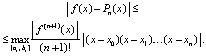
Разности x – xr, где xr – узлы интерполяции, на достаточно малом подынтервале – правильные и соответственно малые по модулю дроби. Модуль произведения дробей 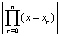 дополнительно уменьшает модуль остаточного члена. Наконец,
дополнительно уменьшает модуль остаточного члена. Наконец, 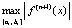 тем меньше, чем меньше длина подынтервала
тем меньше, чем меньше длина подынтервала 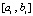 . Эти рассуждения применимы для преобразованных полиномов Лагранжа (16), (17) и Ньютона (18), (19). Однако с помощью обратной замены
. Эти рассуждения применимы для преобразованных полиномов Лагранжа (16), (17) и Ньютона (18), (19). Однако с помощью обратной замены 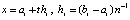 можно непосредственно оценить их остаточный член [7, 10], в результате оценка погрешности примет вид (13), (15). Мажоранта
можно непосредственно оценить их остаточный член [7, 10], в результате оценка погрешности примет вид (13), (15). Мажоранта 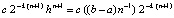 показывает, что чем больше число подынтервалов
показывает, что чем больше число подынтервалов 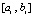 на
на 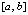 (соответственно, чем меньше их длина), тем меньше погрешность кусочной интерполяции.
(соответственно, чем меньше их длина), тем меньше погрешность кусочной интерполяции.
Арифметика с плавающей точкой искажает оценки погрешности многих классических методов, исторически и математически для такой арифметики не предназначавшихся. Эти методы строились над полем вещественных (комплексных) чисел в абстрактном понимании числа, без ограничения разрядности, при естественной записи разрядов с фиксированной точкой. В компьютерной реализации арифметики с плавающей точкой для выравнивания порядков выполняется сдвиг мантиссы в ограниченной разрядной сетке с неизбежной потерей значащих цифр числа. Это происходит при выполнении практически каждой арифметической операции. С алгебраическим полем вещественных (комплексных) чисел такая арифметика имеет мало общего: в компьютере не те числа, не то сложение, не то умножение, не то деление. Классические алгоритмы не эквивалентны их компьютерной реализации и искажаются ею. Так, расположение узлов интерполяции в полиноме Лагранжа по схеме Чебышева [3] для наименьшего отклонения от нуля остаточного члена интерполяции сохраняет вещественный тип узлов, которые предварительно вычисляются через тригонометрические функции. В результате применение этой схемы в компьютере для кусочной интерполяции элементарных функций не позволяет превысить точность приближения порядка 10–12. Использование других классических полиномов [3] для кусочной интерполяции тех же функций даст точность приближения не выше 10–15 (Delphi, C++).
Целесообразно отметить, что тема кусочно-интерполяционного вычисления функций сохраняет актуальность [11]. Для случая функций двух переменных аналог изложенного метода представлен в [12]. Перенос метода, описанного выше для ОДУ, на случай гиперболических уравнений в частных производных изложен в [13]. Непосредственно тема численного интегрирования ОДУ неизменно актуальна в отечественных и зарубежных работах [14, 15].
Заключение
Действительные функции одной действительной переменной приближаются алгебраическими полиномами с числовыми коэффициентами с применением кусочной интерполяции. Полиномы получены преобразованием интерполяционных полиномов Лагранжа и Ньютона с равноотстоящими узлами при помощи алгоритма восстановления коэффициентов полинома по его корням, отличного от формул Виета, а также не использующего уравнения Ньютона для симметрических функций корней. Метод применяется для приближения подынтегральных функций, что приводит к реализации аналога подхода Ньютона – Котеса для произвольной степени интерполяционного полинома. Вычисление интегралов и функций выполняется с точностью до 10–20. Метод позволяет вычислять производные функций с точностью до 10–16. Приближенное решение задачи Коши для ОДУ построено с использованием кусочной интерполяции на основе интерполяционных полиномов Лагранжа и Ньютона, эквивалентно преобразованных к виду алгебраических полиномов с числовыми коэффициентами. С помощью преобразованных полиномов приближаются правые части уравнений системы. Первообразные от полиномов – координаты приближенного решения. Процесс итерационно уточняется, в результате решение приближается со сравнительно высокой точностью. Численный эксперимент показывает вычислительную устойчивость решения жестких и нежестких задач в приемлемых границах трудоемкости.
Библиографическая ссылка
Ромм Я.Е., Джанунц Г.А. КУСОЧНАЯ ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ, ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ С ПРИЛОЖЕНИЕМ К РЕШЕНИЮ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ // Современные наукоемкие технологии. 2020. № 12-2. С. 291-316;URL: https://top-technologies.ru/ru/article/view?id=38448 (дата обращения: 30.12.2025).
DOI: https://doi.org/10.17513/snt.38448