Пусть психологическое поведение роботов является ответной реакцией на стимул – звуковой сигнал, поступающий в приемные устройства робота. В таком случае можно разработать математическую модель расчета эмоционального воспитания робота, которая будет зависеть от амплитуды звукового сигнала, который воздействует на робота.
Любая функция, которая удовлетворяет требованиям, описанным в работе [1], является эмоцией робота, то есть функция
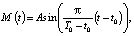(1)
где M(t) – эмоции робота в момент времени t, T0 – верхняя граница интервала, на котором вычисляется эмоция робота, t0 – нижняя граница интервала, на котором вычисляется эмоция робота, A – амплитуда звукового сигнала, воздействующего на робота; также моделирует эмоцию робота. Тогда эмоциональное воспитание робота на i-м такте может быть представлено в виде формулы
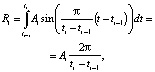(2)
где i – порядковый номер воспитательного такта [2], ti-1 – начало i такта, ti – конец i такта, Ai – среднее значение амплитуды звукового сигнала, измеренное в течение такта i.
Предположим, что длина такта постоянна и обозначим ее β = ti – ti-1 = const, тогда
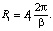(3)
Математическая модель непрерывного эмоционального воспитания роботов с неабсолютной памятью, приведенная в работе [1], может быть преобразована следующим образом:
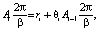(4)
где i – порядковый номер воспитательного такта [2], ri – элементарное воспитание робота, полученное им в конце такта i,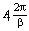 
– суммарное воспитание, полученное роботом в конце такта i, θi – коэффициент памяти для такта i, 0 < θi ≤ 1 – δ, 0 < δ = const < 1.
Будем полагать, что
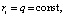
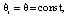(5)
тогда равенство (4) можно записать в виде
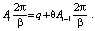(6)
Равенство (6) назовем математической моделью простейшего воспитания робота, выраженного через амплитуду звукового сигнала.
В работе [3] вводится понятие фиктивного такта, которое обозначает временные перерывы между воспитаниями. Для фиктивных тактов справедливо равенство ri = 0, тогда формула (4) преобразуется в равенство
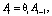(7)
которое при условиях (5) примет вид
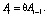(8)
Так как амплитуда звукового сигнала – это положительное значение, то Ai > 0, таким образом, фиктивным тактом можно считать такт, для которого справедливо неравенство
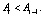(9)
В работах [4, 5] и других приведены результаты многочисленных исследований психологического поведения роботов на основе моделей простейшего воспитания, которые лежат в основе уравнений (6) и (8).
В силу того, что на практике при создании психологического аналога человека соотношения (5) справедливыми не являются, требуется аппроксимировать реальный воспитательный процесс, описанный уравнениями (4) и (7), используя модели простейшего воспитания (6) и (8).
Целью исследования является разработка математической модели аппроксимации реального воспитания, рассчитанного на основе амплитуды звукового сигнала, воздействующего на робота, с помощью простейшего эмоционального воспитания, а также реализация компьютерной программы для определения его параметров: коэффициента памяти – θ, элементарного воспитания – q и предельного воспитания.
Математическая модель
Пусть имеются численные значения эмоционального воспитания, выраженные через амплитуду звукового сигнала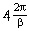 
, где i определяет порядковый номер такта воспитания.
Тогда для вычисления коэффициентов памяти θ только при фиктивных тактах необходимо решить задачу по определению безусловного экстремума функции I(θ):
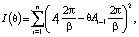
где n – количество выполненных измерений.
Решая уравнение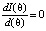 
, получим следующее соотношение для вычисления коэффициента памяти θ:
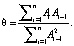(10)
Предположим, что во время экспериментальных измерений были как такты, так и фиктивные такты.
Запишем функцию J(θ, q) в следующем виде:
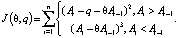
Очевидно, что для аппроксимации простейшим воспитательным процессом воспитания, являющегося амплитудой звукового сигнала, нужно решить следующую задачу – найти
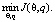(11)
Вычисляя первые производные функции J(θ, q) по переменным θ и
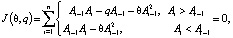(12)
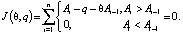(13)
Легко показать, что система уравнений (12)–(13) эквивалентна следующей системе:
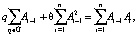(14)
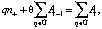(15)
где Ω – множество тех номеров i, для которых справедливо неравенство Ai > Ai-1, n+ – количество элементов в множестве Ω.
Решая систему уравнений (14)–(15), получим соотношения для искомых величин θ и q:
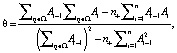(16)
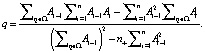(17)
Заметим, что система уравнений (16)–(17) позволяет найти решения θ и q только в том случае, когда множество Ω не пусто, в противном случае простейшее воспитание описывается только коэффициентом памяти θ, который удовлетворяет равенству (10).
Программная реализация модели
Для определения параметров простейшего воспитания θ и q, а также предельного воспитания, аппроксимирующего реальное воспитание, которое рассчитывается с помощью звукового сигнала, было разработано настольное приложение на языке Java.
Разработанная компьютерная программа позволяет записать аудиофайл в формате wav с помощью обычного микрофона либо подключенного к компьютеру, либо встроенного в компьютер. Также программа на основе амплитуды звукового сигнала, извлеченной из записанного аудиофайла, рассчитывает эмоциональное воспитание робота и выводит на экран график зависимости эмоционального воспитания от времени. Интервал, через который производится расчет эмоционального воспитания, задается пользователем приложения. Когда весь файл проанализирован и все значения эмоционального воспитания рассчитаны, то вычисляются требуемые параметры простейшего обучения: коэффициент памяти, элементарное воспитание и предельное воспитание.
Когда пользователь запускает приложение, он попадает на форму «Запись». На этой форме пользователь может записать аудиофайл, который будет использован для расчета параметров простейшего воспитания. Чтобы начать аудиозапись, пользователь должен выполнить следующую последовательность действий:
1) нажать кнопку «Выбрать», после этого откроется окно, в котором необходимо выбрать каталог, в который будет сохранен аудиофайл;
2) ввести название файла в поле «Файл»;
3) нажать кнопку «Старт», после этого появится надпись «Запись...», указывающая на то, что процесс запустился успешно.
Чтобы остановить запись, пользователю необходимо нажать кнопку «Стоп». Аудиофайл будет сохранен по пути, указанному в поле «Директория», с названием из поля «Файл».
После этого пользователь может перейти на форму «Обучение», изображенную на рисунке.
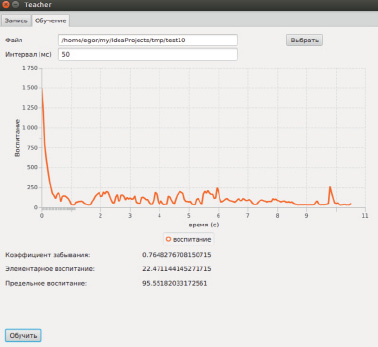
Форма расчета параметров
Для расчета параметров простейшего воспитания пользователю необходимо:
1) нажать кнопку «Выбрать», после этого откроется окно, в котором необходимо выбрать аудиофайл формата wav;
2) ввести интервала дискретизации такта в миллисекундах;
3) нажать кнопку «Обучить».
Программа разбивает файл на интервалы указанной длины, определяет среднюю амплитуду звукового сигнала на каждом интервале и, используя ее, рассчитывает элементарное воспитание q и коэффициент памяти θ для простейшего воспитания. На рисунке изображен график зависимости эмоционального воспитания робота, рассчитанного с помощью амплитуды звукового сигнала, от времени. Видно, что на протяжении 10 с было воздействие звуковым сигналом с различной громкостью. Коэффициент памяти эмоционального робота, реагирующего на данный звуковой сигнал, равен примерно 0.765, то есть эмоциональный робот с каждым тактом будет забывать четверть полученной им информации, при этом его воспитание с каждым тактом воспитания увеличивается на 22.471. Предельное воспитание для смоделированного эмоционального робота составляет 95.552.
Обоснование выбора языка программирования
В качестве языка программирования был выбран Java, так как он обладает следующими преимуществами:
1) кроссплатформенность. Программа может быть скомпилирована под различные платформы (Linux, Windows);
2) наличие api для работы со звуком;
3) наличие инструментов для создания интерфейса десктопного приложения;
4) наличие полной документации и развитого сообщества разработчиков;
5) относительная простота разработки;
6) наличие удобной среды разработки.
Заключение
Таким образом, в настоящей статье приведена математическая модель расчета эмоционального воспитания робота на основе воздействующего на него звукового сигнала. Приведены соотношения для расчета элементарного воспитания, коэффициента памяти и предельного воспитания на основе реального воспитания робота, рассчитанного с помощью амплитуды звукового сигнала. Описана компьютерная программа, которая на основе звукового сигнала рассчитывает эмоциональное воспитание робота, строит его зависимость от времени, выводит эту зависимость на экран в виде графика и рассчитывает параметры простейшего воспитания: элементарное воспитание, коэффициент памяти и предельное воспитание.
Библиографическая ссылка
Пенский О.Г., Шестаков Е.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЫЧИСЛЕНИЯ ПАРАМЕТРОВ ПРОСТЕЙШЕГО ВОСПИТАНИЯ РОБОТОВ, РЕАГИРУЮЩИХ НА ЗВУКОВЫЕ СТИМУЛЫ // Современные наукоемкие технологии. – 2020. – № 12-2. – С. 286-290;URL: https://top-technologies.ru/ru/article/view?id=38447 (дата обращения: 19.04.2024).