В настоящее время очень большое внимание уделяется альтернативным источникам энергии [1]. Это связано, в основном, с высокой стоимостью энергоносителей, а также с ухудшением экологической обстановки в мире. При этом классические системы также обладают и существенными недостатками, такими как увеличение температуры дымовых газов, повышение коэффициента избытка воздуха и иные, приводящими к увеличению потерь при производстве тепловой энергии [2]. Для повышения эффективности работы системы отопления жилого или производственного помещения используют различные схемы и методы получения тепловой энергии, к ним относятся и системы с импульсной циркуляцией теплоносителя. Подобные системы приведены, в том числе, и в наших ранних работах [3, 4]. Один из аппаратов, используемый для повышения эффективности системы отопления, – кавитатор [5, 6]. Этот аппарат является альтернативным вариантом замены любого отопительного котла. В нем нагрев воды осуществляется за счет кавитации. Этот эффект возникает в результате резкого снижения давления, когда локально в слое воды образуются пузырьки пара, при резком схлопывании которых происходит гидравлический удар и осуществляется нагрев воды [7, 8, 9]. При этом, как показывают многие исследования, чем выше изначальное давление воды, тем сильнее эффект от кавитации [10]. Так как использование импульсного режима течения позволяет существенно повысить давление воды, то и эффект от кавитации будет значительно выше. Для определения оптимальных параметров режима работы предлагаемой системы теплоснабжения на основе кавитатора проведено математическое моделирование.
В данной работе представлено моделирование режимов работы струйного кавитатора в импульсном режиме течения теплоносителя с целью определения оптимальных параметров его функционирования.
Для достижения цели поставлены следующие задачи:
– разработать схему лабораторной установки со струйным кавитатором, работающим в импульсном режиме;
– построить энергетическую цепь полученной системы;
– получить уравнение математической модели;
– построить амплитудно-частотную и фазо-частотную характеристики полученной системы;
– определить оптимальные параметры работы кавитатора.
На рис. 1 показана предлагаемая принципиальная схема лабораторной установки струйного кавитатора с импульсной циркуляцией течения теплоносителя.
Схема работает следующим образом: циркуляционный насос 1 направляет жидкость из бака аккумулятора 3 по двум контурам: первый контур – через ударный узел 2 [7] в бак аккумулятора 3; второй контур – через обратный клапан 4 и кавитатор 5, где происходит нагрев жидкости, в бак аккумулятора 3. Генерируемые в ударном узле 2 гидравлические удары повышают давление во втором контуре, тем самым существенно увеличивая эффективность работы кавитатора [9]. Гидроаккумулятор 6 сглаживает давление, создаваемое ударным узлом 2. Датчики температуры и давления 7 и 8 соответственно регистрируют параметры работы системы.
Для нагрева жидкости в лабораторной установке используется струйный кавитатор [10], представленный на рис. 2.
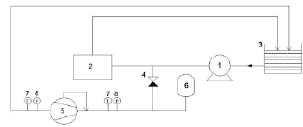
Рис. 1. Схема лабораторной установки с импульсной циркуляцией теплоносителя: 1 – циркуляционный насос; 2 – ударный узел; 3 – бак аккумулятора; 4 – обратный клапан; 5 – кавитатор; 6 – гидроаккумулятор; 7 – датчики температуры; 8 – датчики давления
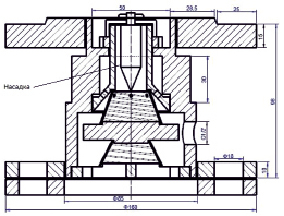
Рис. 2. Схема струйного кавитатора
Моделирование начнем с построения энергетической цепи струйного кавитатора, представленной на рис. 3 [10].
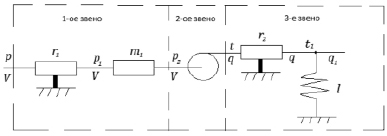
Рис. 3. Энергетическая цепь c использованием кавитатора
Данная цепь состоит из трех звеньев. Первое звено гидравлическое, учитывает потери на трение потока при помощи активного сопротивления r1, инерционные свойства потока характеризуются массой жидкости m1 в трубопроводе. Второе звено – преобразовательное, преобразует давление p2 и объемный расход v жидкости на входе кавитатора в температуру t и удельный тепловой поток q. Третье звено – тепловое, учитывает потери тепла в окружающую среду и аккумулирование теплового потока с податливостью L.
Уравнение звеньев цепи:
1-оe 2-e 3-e
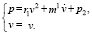
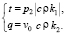
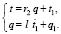
Составим частотную функцию энергетической цепи как отношение параметров выхода к параметрам входа в соответствии со схемой, изображенной на рис. 4.
или 
Рис. 4. Изображение входных и выходных переменных предлагаемой системы
Представим выходные переменные в виде постоянной составляющей и отклонения:
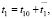
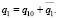(1)
Далее запишем уравнение на давление в преобразовательном звене p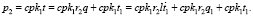2:
(2)
Уравнение на объем жидкости V будет:
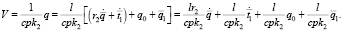(3)
Уравнение на приращение объема жидкости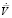 
:
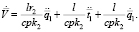(4)
Уравнение на V2:
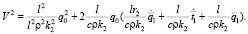(5)
Уравнение на температуру нагрева t:
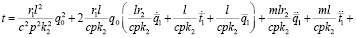
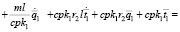
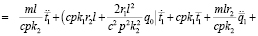(6)
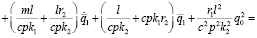
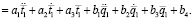
Введем коэффициенты для упрощения уравнения 6:
, 
, 
,
, 
, 
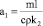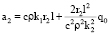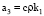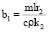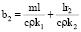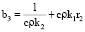. (7)
С учетом введенных коэффициентов уравнение 6 принимает вид:
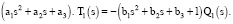(8)
При этом комплексное сопротивление цепи:
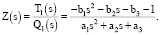(9)
Частотная функция цепи:
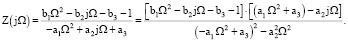(10)
Действительная часть функции:
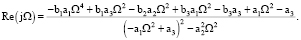(11)
Мнимая часть функции:
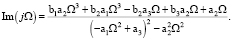(12)
Амплитудно-частотная характеристика цепи:
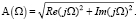(13)
Фазо-частотная характеристика:
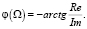(14)
Результаты исследования и их обсуждение
Кавитатор на рис. 2 имеет возможность замены зазора проходного сечения за счет смены конусовидных насадок различных диаметров. Для определения оптимальных параметров струйного кавитатора построим по уравнениям 13 и 14 амплитудно-частотные и фазо-частотные характеристики для трех различных зазоров проходного сечения.
Для этого зададимся параметрами энергетической цепи (первый зазор – 0,1 мм):
1) 
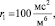
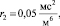m1 = 100 кг, 
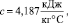ρ = 1000, k1 = 1,3, k2 = 1,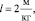 
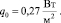
Таблица 1
Расчетные коэффициенты для определения частотных характеристик (1-я конструкция)
|
a1 |
a2 |
a3 |
b1 |
b2 |
b3 |
|
0,143 |
544,31 |
5443,1 |
0,007 |
0,11 |
272,16 |
По результатам вычислений частотных характеристик построим графики амплитудно-частотной характеристики (АЧХ) и фазо-частотной характеристики (ФЧХ) цепи (рис. 5, 6).
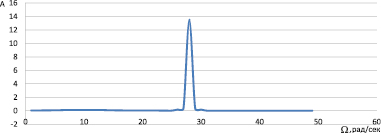
Рис. 5. Амплитудно-частотная характеристика (АЧХ) цепи (1-я конструкция)
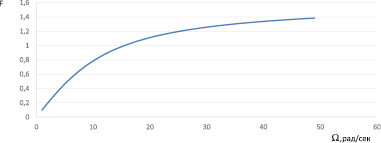
Рис. 6. Фазо-частотная характеристика (ФЧХ) цепи (зазор 0,1 мм)
Как видно из графика (рис. 5), имеется характерное увеличение амплитуды более 13 раз на частоте 25–30 рад/с, что свидетельствует о резком увеличении температуры потока при данном значении.
Изменим значения параметров энергетической цепи и для них также построим характеристики (второй зазор – 0,09 мм):
2) 
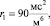
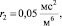m1 = 200 кг,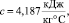 
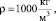k1 = 1,3, k2 = 1,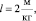 
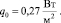
Таблица 2
Расчетные коэффициенты для определения частотных характеристик (2-я конструкция)
|
a1 |
a2 |
a3 |
b1 |
b2 |
b3 |
|
0,239 |
8491,236 |
3265,86 |
0,117 |
0,184 |
163,3 |
По результатам расчета частотных характеристик построим графики амплитудно-частотной характеристики (АЧХ) и фазо-частотной характеристики (ФЧХ) цепи для зазора 0,09 мм (рис. 7, 8).
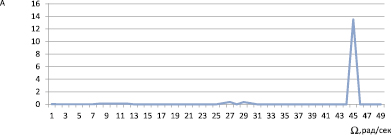
Рис. 7. Амплитудно-частотная характеристика (АЧХ) цепи (2-й зазор)
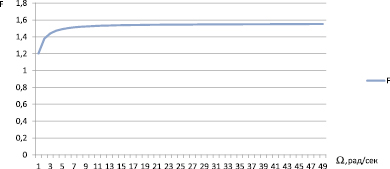
Рис. 8. Фазо-частотная характеристика (ФЧХ) цепи (2-я конструкция)
Как видно из графика (рис. 7), имеется характерное увеличение амплитуды более 13 раз на частоте 44–45 рад/с, что свидетельствует о резком увеличении температуры потока при данном значении.
Построим амплитудно-частотную и фазо-частотную характеристики для следующих параметров энергетической цепи (третий зазор – 0,05 мм):
3) 
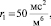
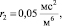m1 = 300 кг,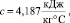 
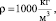k1 = 1,3, k2 = 1,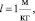 
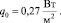
Таблица 3
Расчетные коэффициенты для определения частотных характеристик (3-я конструкция)
|
a1 |
a2 |
a3 |
b1 |
b2 |
b3 |
|
0,209 |
217,725 |
4354,48 |
0,0105 |
0,162 |
217,724 |
По результатам расчета частотных характеристик построим графики амплитудно-частотной характеристики (АЧХ) и фазо-частотной характеристики (ФЧХ) цепи (рис. 9, 10).
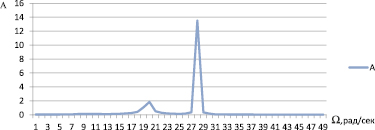
Рис. 9. Амплитудно-частотная характеристика (АЧХ) цепи (3-я конструкция)
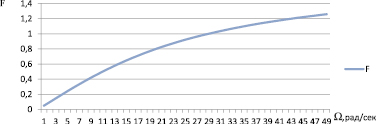
Рис. 10. Фазо-частотная характеристика (ФЧХ) цепи (3-я конструкция)
Как видно из рис. 9, имеются характерное увеличение амплитуды более 13 раз на частоте 28–29 рад/с и незначительное увеличение амплитуды в 2 раза на частоте 18–20 рад/с.
Заключение
В процессе моделирования была разработана математическая модель в виде дифференциальных уравнений на приращение, полученных с помощью энергетических цепей. Уравнения решались в частотном виде при варьировании следующих параметров: масса теплоносителя и активное сопротивление кавитатора. В результате моделирования выявлено, что наибольшее влияние оказывает масса теплоносителя, поэтому для увеличения эффекта необходимо увеличить расход теплоносителя. Сравнивая амплитудно-частотные характеристики (АЧХ) и фазо-частотные характеристики (ФЧХ) цепи, можно сделать вывод, что оптимальная частота колебаний потока теплоносителя в импульсном режиме течения для выбранной конструкции кавитатора составляет 25–30 рад/c при зазоре проходного сечения кавитатора 0,1 мм, 44–45 рад/с – для зазора 0,09 мм и 44–45 рад/с – для зазора 0,05 мм. Увеличение величины нагрева на указанных частотах составляет более 13 раз. Полученные результаты моделирования могут быть использованы для определения и выбора параметров варьирования во время проведения физического эксперимента, а также в реальных импульсных системах теплоснабжения на основе кавитатора.
Библиографическая ссылка
Левцев А.П., Лысяков А.И., Давыдов А.Е., Неясов А.С., Янкин В.О., Баранов И.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СТРУЙНОГО КАВИТАТОРА В ИМПУЛЬСНОМ РЕЖИМЕ ТЕЧЕНИЯ ТЕПЛОНОСИТЕЛЯ // Современные наукоемкие технологии. – 2020. – № 12-1. – С. 78-85;URL: https://top-technologies.ru/ru/article/view?id=38414 (дата обращения: 25.04.2024).