Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Горяев В.М. 1 Бембитов Д.Б. 1 Сумьянова Е.В. 1 Учурова Е.О. 1 Саргинов С.С. 1 Горнаков А.Л. 1 Кукарека С.А. 1

---

1 ФГБОУ ВО «Калмыцкий государственный университет им. Б.Б. Городовикова»

В работе исследуется подход интеллектуального анализа данных (ИАД) для прогнозирования стихийного бедствия при степных пожарах. Рассматриваются несколько различных методов анализа данных и как минимум пять различных специальных методов выбора признаков (пространственные, временные, компоненты канадского индекса пожаров, погодные атрибуты и собственные разработанные классы на языке разработки нейросетей). На данный момент протестированы программные комплексы анализа на реальных данных, собранных в южных районах Калмыкии. В исследовании будут использованы открытые данные метеостанций, собственные временные ряды, собранные в течение последних трех лет, проверены различные методы интеллектуального анализа данных и как минимум пять метеорологических входов, что позволит прогнозировать сгоревшую область небольших и средних пожаров, область пыльных бурь и т.п. Такие прогнозы особенно полезны для улучшения управления ресурсами пожаротушения (например, приоритетность целей для воздушных и наземных пожарных экипажей) и реагирования на другие природные ЧП. В результате построены прогнозы на базе метеоданных и годовых данных по пожарам за период с 2015 по 2020 г. Результаты показывают, что модель дерева решений является наиболее подходящим кандидатом для модели прогнозирования степных пожаров. Выбранная модель учитывает как метеорологические данные, так и изображения для раннего прогнозирования пожаров системы FIRMS.

Статья в формате PDF

0 KB

машинное обучение

степные пожары

модель Бокса – Дженкинса

прогноз

авторегрессия

1. Asamoah-Boaheng M. Using SARIMA to Forecast Monthly Mean Surface Air Temperature in the Ashanti Region of Ghana. International Journal of Statistics and Applications. 2014. no. 4. P. 292–298.

2. Box G.E., Jenkins G.M. and Reinsel G.C. Time series analystrol: Forecasting and Control. John. Wiley & Sons, Hoboken. 2015. P. 456.

3. Goryaev V.M., Kazakova G.Y., Bembitov D.B., Dzhakhnaeva E.N., Sangadjieva E.V. Development of a statistical forecast model to improve accuracy based on statistical analysis of weather historical data for the Kalmyk region. Earth and Environmental Science. 2019th International Symposium on Earth Sciences: History, Contemporary Issues and Prospects. Bristol: IOP Publishing, 2019. Р. 012058. DOI: 10.1088/1755-1315/350/1/012058.

4. Cortez P., Morais A. A Data Mining Approach to Predict Forest Fires using Meteorological Data. Proceedings of the 13th Portuguese Conference on Artificial Intelligence «New trends in artificial intelligence» (EPIA 2007), Guimar?es, Portugal, December 2007. Lisboa: APPIA, 2007. P. 512–523.

5. Жерон О. Прикладное машинное обучение с помощью Scikit-Learn, Keras и TensorFlow. М.: Вильямс, 2020. 1040 с.

Цель исследования: решение проблемы прогнозирования степных пожаров в южных районах Калмыкии на основе интеллектуального анализа данных. Для достижения этой цели одним из вариантов является использование автоматических средств на основе местных датчиков, например метеорологических станций и местных мониторинговых социальных сетей. В действительности, метеорологические условия (например, температура, ветер), как известно, влияют на степные пожары, и некоторые пожарные индексы, такие как разрабатываемый нами индекс степных пожаров (FSI) на базе индекса пожароопасной погоды (FWI), используют как дополнительный фактор к наборам данных.

В свое время в Канаде была создана система раннего предупреждения на базе оценки пожарной опасности, основанная на моделях атмосферных воздействий. Ежедневные прогнозы состояния пожарной опасности основаны на системе оценок пожарной опасности лесной службы США (NFDRS) и канадской системе оценки индекса пожарной погоды.

Материалы и методы исследования

На активность возникновения пожаров влияют четыре основных фактора: состояние растительности (топливо), синоптические данные, компоненты воспламенения и человеческий фактор [1]. Там, где имеется топливо, погода является наиболее важным фактором в формировании пожарных режимов во многих районах мира [2]. Пожары – это глобальное явление, распространяющееся на территории от бореальных лесов Канады и Сибири до монгольских степей.

Анализ состоит из двух частей: а) проводится дополнение недостающих значений для создания полных наборов данных; б) выполняется ряд алгоритмов машинного обучения для построения прогнозных моделей на основе вмененных данных.

Для объединенного набора данных значения метеоданных были получены на станциях г. Элисты № 1 (1966–2019) и № 2 (1927–2019). Кроме того, для получения метеоданных использовались открытые источники: Hydrometcenter of Russia и NOAA.

Данные из набора Elmet1 [3] демонстрируют общемировой тренд на увеличение температуры за полвека +1,1 °С, сопоставление среднегодовой температуры в период 1928–1937 и, соответственно, 1998–2019 показывает еще большую разницу (+1,81 °С). Cредний показатель влажности для Калмыкии – 68,882, c 1991 г. влажность возросла до 71,388, (при соответствующих температурах 9,361 и 10,212).

В Канаде будущая пожарная активность часто оценивается с помощью Burn-P3, имитационной модели, используемой для оценки пространственной вероятности возгорания (ПВВ) путем моделирования очень большого количества пожаров. В данном исследовании были модифицированы следующие факторы в будущих прогнозах ПВВ: 1) топливо (травяная растительность), 2) световая интенсивность и 3) погода (ежедневные условия и площадь пожаров).

Настоящий набор данных для исследования охватывает метеорологические и пространственно-временные данные о степных пожарах (в 2016–2019 гг.) на полигоне T1, T2 (45.863 °, 46.234 °), использовалась сетка 24×24 узлов, что обеспечивало горизонтальное разрешение 5 км для области T1, 4 км – для области T2. Экспериментальные работы проводились на восьми участках. Все участки характеризуются различными типами растений степных сообществ, климат засушливый с характерным дефицитом воды с мая по сентябрь. Целевой атрибут – общая площадь сгоревшей степи в гектарах (га). Соответствующие погодные данные – данные датчиков в момент обнаружения пожара. Также данные DMC, DC, FFMC – компоненты системы канадского индекса пожаров (FWI), которая измеряет влияние влажности почвы и растительности, ветра и световой радиации на развитие пожара. Эти поля вычисляемые, они были рассчитаны на базе ежесуточных наблюдений за метеоданными.

Относительные координаты осей в исследуемом полигоне: X: от 1 до 9, Y: от 2 до 9, месяц, день недели, индекс FFMC: от 0,0 до 100,0, индекс DMC: 1,1 до 300,0, индекс DC: от 7,9 до 890,0, индекс ISI: от 0,0 до 60,0, температура в градусах Цельсия: от 5 до 42, относительная влажность воздуха в %: от 15,0 до 100, ветер – скорость ветра в км/ч: от 0,0 до 12, дождь в мм/м2 : от 0,0 до 6, SA – солнечная радиация в кВч/м2: от 1,0 до 6, площадь сгоревшего участка местности (в га): от 0,00 до 1000,0.

Результаты исследования и их обсуждение

В наше время разработаны различные алгоритмы и системы для прогнозирования площади сгорания, времени степного пожара. В этом исследовании были изучены и проверены различные алгоритмы машинного обучения. Для шаблона взят набор данных Cortez – Morais [4].

Данные для работы были получены на основе региональной численной модели прогноза погоды MM5, где представлены временные атмосферные процессы над территорией юга РФ, метеоданные, файлы пожароопасности из данных системы FIRMS, также длинные наборы временных рядов о пожарах (в будущем они будут существенно дополнены данными из собственных наборов данных, которые в настоящее время находятся в фазе сбора и накопления данных). Набор данных Cortez – Morais включает временную и пространственную компоненты из Канадского индекса пожарной погоды (FWI) вместе с четырьмя погодными условиями для разработки регрессионной модели для предсказания площади сгоревшей степи. Набор данных FIRMS содержит данные по пожарам. Каждое изображение связано с черно-белым (бинарным) наземным изображением, аннотациями и дескрипторами.

Начальные и граничные условия для локализации метеомоделей формировались с использованием данных собственного объективного анализа (табл. 1). Такой анализ метеополей выполняется на базе обработки начальных приближений данных метеорологических полей и синоптических данных (ветре, температуре, световой радиации и относительной влажности воздуха на изобарических поверхностях).

Набор данных о пожарах, использовавшийся в настоящем исследовании, охватывал более длительный период, но был в итоге сокращен, при этом качество данных о пожарах было обеспечено главным образом за счет интенсивного мониторинга пожаров.

Таблица 1

Набор данных

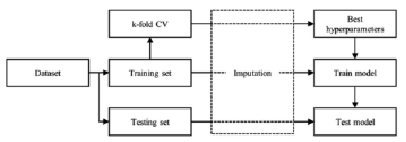
Рис. 1. Методология моделирования

Для работы импортируются следующие библиотеки для различных моделей ML. Для кодирования выбран Python 3.7 дистрибутива Miniconda 3.

Процесс решения ориентируется на метрику Root Mean Squared Error (RMSE), где происходит отбор наивысших по релевантности элементов для составления прогноза.

Открытие набора данных в формате csv: fire = pd.read_csv(r"c:/input/SteepFire106.csv")

Выбор оптимальных моделей

Анализ состоит из двух частей:

1) проводится дополнение недостающих значений для создания наборов данных;

2) выполняется ряд алгоритмов машинного обучения для построения прогнозных моделей на основе вмененных данных.

Иллюстрация конкретных компонентов анализа приведена на рис. 1.

Линейная регрессия. Для данного исследования работа выполнялась с использованием как статистического подхода, так и подходов машинного обучения. Линейная регрессия используется для моделирования причинно-следственных связей между параметрами в наборах данных. Существуют предположения, которые представляют модель линейной регрессии в отношении применяемого набора данных: линейность отношений, мультиколлинеарность, автокорреляция, гомоскедастичность. Для работы с линейной регрессией используется пакет scikit-learn [5].

Для создания и проверки моделей ML разделяем выборки из набора данных:

steppe_fire = st_train_set.drop('площадь', axis=1)

steppe_fire_labels = st_train_set.площадь.copy()

При наблюдении за графиками обнаруживается отсутствие четкой линейности, поэтому выполняются различные методы преобразования данных, для достижения требуемой линейности: удаляются выбросы в данных, исправляются нелинейности в целевом объекте и устраняется перекос, для достижения нормальности остатков.

Для анализа на гомоскедастичность используется тест Гольдфельда – Квандта (рис. 2).

sms.het_goldfeldquandt(lin_reg.resid, lin_reg.model.exog)

(1.0008349694546035, 0.4975189511232223, 'increasing')

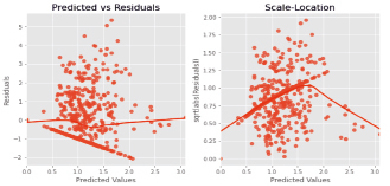
Рис. 2. Анализ на гомоскедастичность

Выбор модели. Функция стоимости (J) линейной регрессии – (RMSE) среднеквадратическая ошибка между регрессором и предиктом. Критерий оценки минимизация RMSE (табл. 2).

Далее конвейер циклически проходит через ряд классификаторов scikit-learn, которые выполняют преобразования и обучающие модели.

Таблица 2

Оценочные параметры моделей

Улучшение гиперпараметров. Далее поиск по сетке, где 'learning_rate': [0.02,0.03,0.04], 'max_depth': [1,2], 'n_estimators': [50,60,70,100]}

grid = GridSearchCV(pipe, param_grid=param_1 cv=5)

{'C': 86.92991511139547, 'gamma': 1.4922453771381408, 'kernel': 'rbf'}

Ниже после понижения размерности используется метод ближайших соседей knn.

knn_train_rmse 12.499096, Mean: 16.074572, Standard deviation: 2.8425216161884084

Для обновления параметров модели с целью уменьшения значения функции стоимости (минимизации RSME) и достижения линии наилучшего соответствия данной модель использует градиентный спуск, который выходит с начальных случайных значений 1 и 2, а затем итеративно обновляет значения, достигая требуемых минимальных затрат: from xgboost import XGBRegressor.

Вычисляется требуемая xgb_train_rmse 0.1920517889114683 и приемлемое отклонение: 5.9212486451887445. В итоговом градиентном бустинге удалось на предикторах добиться погрешности в пределах 9,54. Гиперпараметрическая настройка заметно улучшила результаты, но при этом время работы модели заметно возросло.

Прогноз результата и анализ вклада предикторов и селекция комбинаций. Для получения наиболее точного значения k необходимо протестировать модель для каждого прогнозируемого значения k. После улучшения модель может выполнять прогноз с текущими или другими данными. При сравнении классификаторов по их отчетам, матрицам ошибок, запускается конвейер преобразований с конечной оценкой. Последовательно применяется список преобразований, промежуточными этапами конвейера должны быть «преобразования», то есть необходимо реализовать методы подгонки и преобразования.

Predictions: [4.810951 4.1733847 5.344085 7.4500217]

Labels: [4.21, 4.74, 6.37, 7.9]

Точность модели

Для оценки 95 %-ных доверительных интервалов воспользуемся библиотекой scipy

squared_errors = (final_predictions-y_test)**2

np.sqrt(stats.t.interval(confidence, len(squared_errors)-1, loc=squared_errors.mean(), scale=stats.sem(squared_errors)))

Результат: array([ 3.51330423, 12.65531037])

Прогнозирование пожаров является сложной задачей из-за сложности соответствующих процессов, ограничений в данных наблюдений, а также совпадения и усугубляющего воздействия нескольких факторов. И наиболее верные прогнозы ориентируются на небольшие площади пожаров, что можно проанализировать при квантильном ранжировании по площадям:

steppe_fire.query('(@Qu1 – 1.5 * @Ie) <= площадь <= (@Qu2 + 1.5 * @ Ie)').кат_возг.value_counts()

Диапазон(0-5)- 381 , (5-10)- 60, (10-50)- 41, (50-100)- 4, (>100)- 2

Рассчитанная выше прогнозная точность 83,46 входит в доверительный интервал коридора ошибок. По итогам работы была предложена экономная модель для описания влияния изменчивости климата. В данном исследовании был создан шаблон для наполнения регулярными данными на территории экспериментального полигона как основа для разработки сезонного прогноза степных пожаров в регионе. В этой связи следует отметить, что обобщение предложенного метода является технически простым. Для применения нашего подхода к постоянно обновляемым прогнозам пожаров, охватывающим все триместры года, следует прибегать к сезонным прогнозам, выпускаемым каждый месяц для скользящих трехмесячных периодов.

Заключение

Результаты, полученные при эксперименте, свидетельствуют, что существует достаточная точность для прогнозирования площади пожаров на основе доступной статистики. Градиентный бустинг на предикторах добился приемлемой погрешности в пределах двух единиц, гиперпараметрическая настройка заметно улучшила результаты.

В процессе исследования была изучена и проверена производительность моделей машинного обучения, а именно LinearRegression, DecisionTreeRegressor, RandomSteppeRegressor, SVR и KNN на наборе данных шаблона Кортеса – Мораиса, содержащем 440 экземпляров и 14 атрибутов. Оценка алгоритмов была проведена на основе precision, recall, f-score, accuracy и RMSE, deviation. Из полученных результатов было видно, что KNN работает лучше всего как с точки зрения точности, так и с точки зрения RMSE. Поэтому мы намерены использовать усиленные деревья решений для предлагаемой системы прогнозирования пожаров. Модель KNN имеет точность 83,46 %, что в среднем на 4–6 % выше, чем остальные 4 алгоритма. Преимуществом предлагаемого подхода является сбор данных в режиме реального времени и низкая стоимость по сравнению с другими системами. И для того чтобы иметь убедительные доказательства влияния изменения климата на рост пожароопасности, следует включить более длинные временные ряды спутниковых данных.

В дальнейшем исследования будут продолжаться с учетом индекса засухи Китча – Байрама и комбинированного индекса Китча – Байрама и световой интенсивности, на базе общегодового ожидаемого объема осадков в том или ином месте. Данный индекс важен для определения аномалий в состоянии почвы и растительного покрова. Для улучшения тестовых наборов данных стоит в дальнейшем рассмотреть синтетическую технику для дублирования примеров миноритарных и мажоритарных классов.

Библиографическая ссылка