По сравнению с жесткими параллельными манипуляторами (платформа Стюарта), кабельные, или тросовые, параллельные манипуляторы вместо жестких звеньев используют тросы в качестве исполнительных элементов для управления движением исполнительного устройства (схвата). Согласно анализу литературных источников, кабельные роботы сохраняют основные характеристики традиционных манипуляторов, включая потенциально большое рабочее пространство, простоту перенастройки и реализации, высокую скорость перемещения и высокое соотношение полезной нагрузки к весу. Благодаря этим особенностям, некоторые приложения доступны в различных областях человеческой деятельности, например в строительстве зданий и сооружений [1], астрономических наблюдениях [2], службе спасения [3], обслуживании или реабилитации инвалидов, а также в многофункциональных воздушных роботах [3].
Однако тросовый манипулятор также имеет ряд специфических недостатков. Наиболее распространенным является то, что кабель может находиться только в напряжённом состоянии, т.е. кабель должен быть натянут, чтобы получить фиксированное состояние схвата. Кроме того, провисание кабеля должно учитываться в подвесных кабельных параллельных роботах [4, 5]. Применение рассматриваемой в настоящей работе кинематической схемы позволяет убрать большинство недостатков, присущих тросовым манипуляторам.
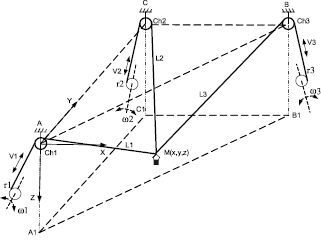
Рис. 1. Кинематическая схема трёхзвенного манипулятора
Цель исследования: разработка тросового манипулятора с улучшенными характеристиками по сравнению с базовой моделью.
Материалы и методы исследования
Базовая кинематика манипулятора параллельной структуры с гибкими звеньями представлена на рис. 1.
На рис. 1 приняты следующие обозначения:
Ch1, Ch2, Ch3 – опорные шкивы звеньев манипулятора;
L1, L2, L3 – текущие длины (обобщённые координаты) звеньев 1–3 манипулятора соответственно;
r1, r2, r3 – радиусы приведения барабанов, связанных с валами электроприводов звеньев манипулятора;
V1, V2, V4 – линейные скорости обобщенных координат звеньев;
ω1, ω2, ω3 – угловые скорости обобщенных координат звеньев;
M (x, y, z) – абсолютные координаты схвата манипулятора.
Кинематическая структура, представленная на рис. 1, может быть описана следующим образом:
- зона обслуживания манипулятора представлена треугольной призмой АВСА1В1С1;
- нерастяжимые нити, представляющие собой звенья манипулятора, одни концы связаны с барабаном мотор-редуктора электропривода вторые концы нити, проходящие через шкив ch1 ch3, связаны между собой и со столом манипулятора;
- обобщенная координата звена равна расстоянию между точками соединения нитей (точка М (x, y, z)) и точкой схода нити со шкива sh-1 ch3 соответствующего звена;
- в абсолютной системе координат, начало которой совпадает с точкой А, координаты точек A (x1, y1, z1), B (x2, y2, z2), C (x3, y3, z3) известны;
- для кинематической схемы, приведенной на рис. 1, координаты шкивов звеньев соответствуют выражениям
x1 = x2=0, y1 = 0, y1 = y2, z1 = z2 = z3 = 0; (1)
- абсолютные координаты положения в зоне обслуживания точки M однозначно определяются величинами обобщенных координат L1÷L3 соответственно.
Уравнения для прямой и обратной задач кинематики подробно рассмотрены в работе [4], там же предложены методы планирования перемещения схвата по заданной траектории.
Основным недостатком базовой модели является эффект колебания перемещаемого груза, особенно сильно проявляющийся при больших значениях абсолютной координаты z.
Результаты исследования и их обсуждение
По сравнению с ближайшим аналогом [6] в работе рассмотрены две дополнительные степени свободы платформы и их влияние на вид уравнений для прямой и обратной задач кинематики. На рис. 2 предложена кинематическая схема манипулятора с гибкими звеньями. Зона обслуживания манипулятора представляет собой параллелепипед c длинами рёбер X1, Y1, Z1, в вершинах которого закреплены мотор-редукторы с барабанами М1–M8. Звенья манипулятора представлены нерастяжимыми нитями L1–L8. Один конец каждого звена связан с барабаном мотор-редуктора, второй конец L1–L8 связан с углом платформы ABCD, причём звенья, связанные с барабанами мотор-редукторов каждого ребра параллелепипеда, попарно крепятся к одному и тому же углу платформы ABCD. Размеры платформы определены величинами AB = CD = а и AD = BC = b. Перемещение платформы в пределах зоны обслуживания достигается за счёт согласованного изменения длины звеньев L1–L8.
В качестве абсолютных координат принято положение геометрического центра платформы – точка M (x, y, z).
Обратная задача кинематики по положению при плоскопараллельном относительно основания или вертикальном перемещении платформы может быть представлена в виде
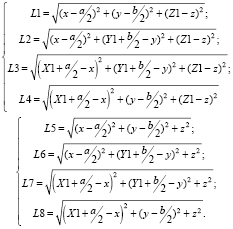(2)
В соответствии с системой уравнений (2) прямая задача о положении может быть представлена как
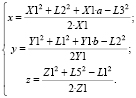(3)
Для некоторых приложений могут быть использованы дополнительные степени свободы платформы, а именно на поворот платформы относительно осей X, Y. Фронтальная проекция манипулятора при вращении платформы вокруг оси Y представлена на рис. 3.
При этом обратная и прямая задачи кинематики для данного манипулятора несколько видоизменяются. На рис. 3 из всего множества показаны три возможных положения платформы манипулятора, обозначенных цифрами 0, 1 и 2. Рабочим положением платформы в рассматриваемом случае является положение 0. При этом появляется дополнительная абсолютная координата φ – угол поворота платформы относительно оси проходящей через центр платформы параллельно оси Y. Уравнения для прямой задачи кинематики манипулятора для случая, представленного на рис. 3, принимают вид
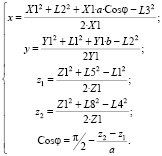(4)
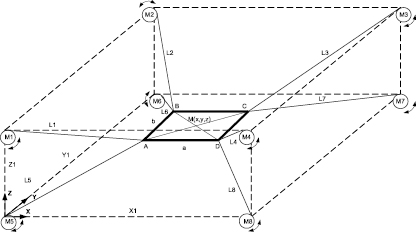
Рис. 2. Кинематическая схема восьмизвенного манипулятора
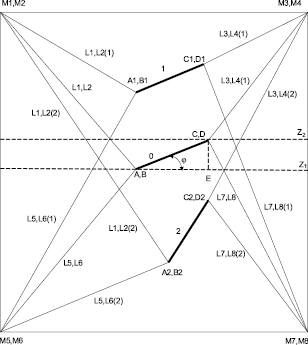
Рис. 3. Фронтальная проекция кинематической схемы восьмизвенного манипулятора
При вращении платформы относительно оси X используется абсолютная угловая координата α и система уравнений для прямой задачи кинематики принимает вид
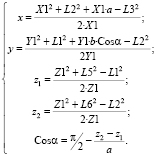(5)
Перемещения платформы с одновременным использованием обеих угловых координат обычно на практике не находят применения.
Система уравнений для обратной задачи кинематики для случая, приведенного на рис. 3 (поворот платформы против часовой стрелки), принимает вид
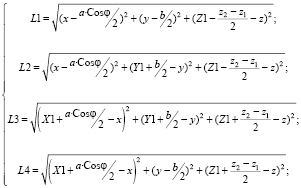(6)
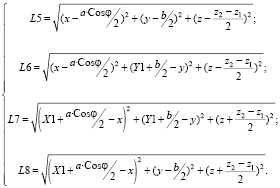
При повороте платформы относительно оси Y в сторону, противоположную показанной на рис. 3, знак при переменной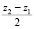 
в уравнении 6 меняется на противоположный. При повороте платформы относительно оси X система уравнений для обратной задачи кинематики может быть представлена как
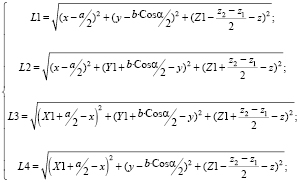(7)
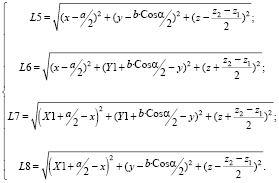
Необходимо отметить, что ввиду односторонней жесткости звена манипулятора на дополнительные обобщенные координаты (углы поворота вокруг осей X и Y) накладываются определенные ограничения, а именно на угол между плоскостью платформы и векторами обобщённых координат не может превышать значения равного π. На рис. 3 это ограничение представлено положениями платформы 2 и 3.
Для представленной кинематической схемы была разработана двухуровневая система управления. Нижний уровень иерархии представлен восемью идентичными САУ вентильно-синхронных двигателей привода звеньев. САУ реализованы с помощью электронных модулей на базе микроконтроллеров семейства STM и драйверов управления вентильно-синхронными двигателями.
Верхний уровень иерархии системы управления реализован программным способом на базе ПК. Все элементы системы управления манипулятором объединены в единую сеть с помощью интерфейса Ethernet, работающую по протоколу UDP.
Всё программное обеспечение написано на языке С (ПК, STM). Экранные копии пользовательского интерфейса информационно-управляющей оболочки представлены на рис. 4, 5. Пользовательский интерфейс содержит таблицу параметров обобщённых координат, таблицу параметров истинных координат клавиши управления и графические окна, показывающие истинное положение платформы в фронтальной и горизонтальной проекциях.
В представленном варианте ПО координаты и угловое положение задаются непосредственной записью необходимых значений в соответствующий столбец таблицы истинных координат. Скорость перемещения по траектории жёстко задана в программном коде. В последующем планируется ввод произвольной скорости и ввод траектории из файла в G-кодах. После инициализации клавиши «Пуск» информационно-управляющая оболочка переходит в режим управления перемещением платформы манипулятора. При этом ПК через заданные промежутки времени, определяемые заданной линейной скоростью платформы, на основе решения прямой и обратной задач (уравнения (4)–(7)) на САУ каждого звена по интерфейсу передаёт текущее значение приращения по каждой из обобщённых координат.
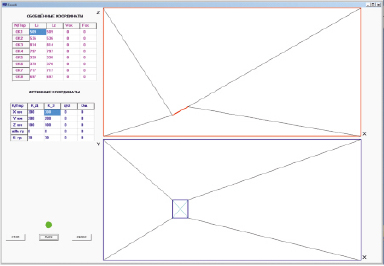
Рис. 4. Экранная копия интерфейса – перемещение с поворотом относительно оси Y
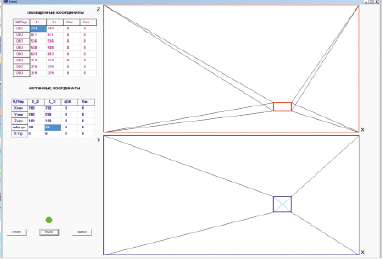
Рис. 5. Экранная копия интерфейса – перемещение с поворотом относительно оси X
В работе [7] приведена методика расчёта пошаговых приращений. При достижении заданного положения перемещение прекращается. В процессе перемещения все параметры обобщённых и истинных координат отображаются в соответствующих таблицах, истинное положение платформы отображается на графических панелях экранного интерфейса.
Предварительные тестовые испытания (без механической части) показали полную работоспособность устройства. Точность позиционирования по каждой из координат составила ±2 дискреты углового положения барабана.
Результаты натурных испытаний системы управления восьмизвенным манипулятором параллельной структуры показали их полную адекватность представленной математической модели.
Заключение
В работе рассмотрен базовый вариант манипулятора параллельной кинематической структуры. Отмечен основной недостаток базовой модели – эффект колебания перемещаемого груза.
Предложена кинематическая схема восьмизвенного манипулятора параллельной структуры с шестью абсолютными координатами. Приведены системы уравнений для решения прямой и обратной задач кинематики подобного манипулятора.
Приведено краткое описание системы управления манипулятором и результаты её тестирования.
Предложенное в работе техническое решение может быть использовано при технической реализации 3D принтера с рабочей зоной до 10 м, а также для перемещения сыпучих грузов.
Библиографическая ссылка
Валюкевич Ю.А., Наумов И.И., Егорышев Н.Е. ИССЛЕДОВАНИЕ КИНЕМАТИКИ ВОСЬМИЗВЕННОГО ПАРАЛЛЕЛЬНОГО МАНИПУЛЯТОРА С ГИБКИМИ ЗВЕНЬЯМИ // Современные наукоемкие технологии. – 2020. – № 11-2. – С. 273-280;URL: https://top-technologies.ru/ru/article/view?id=38374 (дата обращения: 21.11.2024).