В настоящее время, несмотря на бурное развитие сети Интернет и рост скорости передачи данных, остается нерешенной проблема сжатия и очистки информационных сигналов с обеспечением допустимого для пользователя качества передаваемой информации. Особенно это касается видеоинформации, для которой характерен рост занимаемого объема при улучшении качества воспроизведения. В современной науке представлены разнообразные способы обработки информационных сигналов, опирающиеся на существующие математические теории [1]. Методы обработки сигналов до сих пор являются объектом научных исследований. Наиболее оптимальным объектом теоретических и практических исследований информационные сигналы могут быть только тогда, когда представлена математическая модель исследуемого сигнала. Математическая модель дает возможность проводить исследование независимо от физической природы сигнала и особенностей конфигурации его носителя, осуществлять их сравнение, определять степень тождества, проводить классификацию сигналов, разрабатывать системы обработки сигналов.
Математические функции, используемые для моделирования сигналов, могут иметь как вещественную, так и комплексную основу. Использование того или иного математического аппарата определяется простотой и удобством его применения при анализе и обработке сигналов, а также особенностями постановки конкретной задачи. Методы рекурсивного описания сигналов связаны с алгоритмами сжатия информации. Например, к рекурсивному заданию сигналов можно отнести класс алгоритмов сжатия, использующих предиктивные методы. Данные методы применяют экстраполяцию значений амплитуд отсчетов, и, если выполняется условие (Ar – Ap) > d, где d – максимально разрешенная погрешность представления амплитуд, а Ar и Ap – амплитуды исследуемого и предсказанного отсчетов, то отсчет передается, в противном случае он считается избыточным [2].
Предиктивное кодирование широко применяется в алгоритмах MPEG, обеспечивающих сжатие информации в несколько десятков раз [3]. При этом модификация математической модели предиктивного кодирования позволит существенно повысить пороги сжатия информации при сохранении ее качества.
Целью исследования является рассмотрение модификации алгоритма предиктивного сжатия информационных сигналов, основанной на адаптивном алгоритме подбора величины шага рекурсивной экстраполяции по интегральной зависимости накапливаемой ошибки для линейного предсказания различных типов сигнала (гармонического сигнала, суперпозиции гармоник, амплитудно-модулированного сигнала, меандра, сигнала с шумом).
Материалы и методы исследования
Предиктивное кодирование сигналов связано с задачей рекурсивного представления дискретных сигналов. Принцип такой связи достаточно очевиден и заключается в применении предыдущих отсчетов сигнала для перехода к следующим отсчетам.
В соответствии с общим математическим определением, рекуррентными соотношениями называют выражения вида
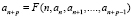, (1)
позволяющие вычислять все члены некоторой последовательности a1, a2, a3, … , если заданы ее первые p членов. Когда рекуррентное соотношение линейно, задача описания множества всех последовательностей имеет аналогию с решением обыкновенного дифференциального уравнения (ОДУ) с постоянными коэффициентами [4]. Простейшая и наиболее употребительная рекурсивная схема называется примитивной рекурсией. Обобщением примитивной рекурсии является возвратная рекурсия.
При использовании терминов «рекуррентное соотношение» и «рекурсия» и соответствующих этим терминам понятий применительно к задачам представления дискретных сигналов мы исходим из того, что в практических приложениях смысловые поля этих терминов, по существу, перекрываются, причем «рекурсия» представляется более общим понятием. Поэтому в дальнейшем мы ограничимся применением только термина «рекурсия», с учетом того обстоятельства, что именно такой термин используется в анализе и синтезе цифровых фильтров.
Рассмотрим вариант алгоритма пошагового рекурсивного кодирования радиотехнических сигналов. Допустим, задан исследуемый сигнал на основе дискретного отсчета времени. Для простоты реализации модели определим шаг предсказания кратным шагу дискретизации.
Каждый последующий отсчет кодировки сигнала будем задавать линейным оператором-предиктором, аргументами которого являются два предшествующих значения амплитуд исследуемого сигнала xi-2, xi-1, а описывающей функцией – рекурсивное значение сигнала xi:
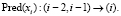(2)
Очевидный вид оператора-предиктора можно задать следующим выражением:
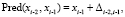(3)
где используется приращение сигнала на основе двух предыдущих отсчетов
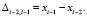(4)
В результате смоделированный отсчет сигнала x`i = Pred(xi-2,xi-1) отличается от реального на величину:
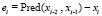(5)
или с условием (3):
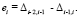(6)
При рассмотрении исследуемого варианта модели пошаговой рекурсии сигнала для разных видов сигналов (гармонического сигнала, суперпозиции гармоник, амплитудно-модулированного сигнала, меандра, сигнала с шумом) анализу подвергалась зависимость накапливаемой ошибки от количества отсчетов.
Использование гармонического сигнала и суперпозиции гармоник как тестовых сигналов обусловлено, во-первых, тем, что семейство базисных функций ansin(wnt) составляет ядро преобразования Фурье, а сами функции вида ansin(wnt) имеют предельную локализацию в частотной области. Здесь учитывается то обстоятельство, что «переложение» подходов к практической реализации вейвлет-преобразования на хорошо понимаемый практиками и привычный (что немаловажно) частотный язык основано на Фурье-преобразовании сигналов. Кроме того, квантование по времени синусоидальных сигналов очень просто представляется аналитически [5]. Напомним также, что в пакете Matlab в ряде типовых примеров используется модельный сигнал sumsin – сумма синусов с разной частотой и амплитудой. Использование суперпозиции гармоник с различными частотами как базового тестового сигнала позволяет рассмотреть различные временные масштабы (медленный, средний и быстрый). Последнее обстоятельство относится как к моделированию пошаговой рекурсии сигнала, так и к вейвлет-анализу на различных уровнях декомпозиции сигнала.
Использование модулированного по амплитуде сигнала как одного из тестовых определяется его частым применением в различных системах связи, в алгоритмах сжатия звуковых и видеосигналов, а также в системах распознавания голоса. Анализ модулированного сигнала позволяет оценить вклад нелинейности в критерии разрабатываемых методов.
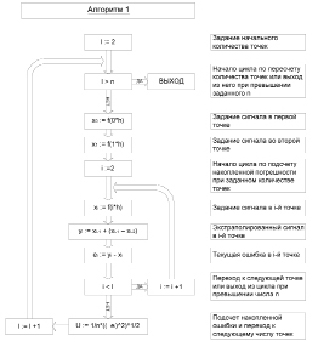
Рис. 1. Алгоритм определения зависимости накапливаемой ошибки от номера отсчета
Меандр является очень удобной моделью импульсного сигнала с кратковременными отсчетами. Такие сигналы отличаются дискретными или интервальными значениями и активно используются в разнообразных устройствах, например в механизмах частотной модуляции и демодуляции, фильтрации радиотехнических сигналов, множителях и преобразователях частот, получателях базового колебания когерентного преобразования информационных сигналов и др. [6].
Сигналы с добавлением шума (все вышеперечисленные типы сигналов с добавлением стационарного случайного процесса) являются базовой моделью, дающей возможность оценки влияния шумов на результативность разрабатываемых методов преобразования сигнала. Использование зашумленных тестовых сигналов предоставляет возможность программно имитировать возможности различных технологий очистки сигнала, в том числе и с применением вейвлет-анализа.
Проверку точности линейной экстраполяции исследуемого сигнала будем реализовывать по нормированной накопленной ошибке n-ого отсчета:
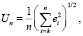(7)
которую в дальнейшем будем именовать накопленной ошибкой, т.е. суммой ошибок во всех точках.
Отметим, что для оптимальности записи нормирование в формуле (7) осуществляется на базе текущего отсчета n, а не на суммарном числе отсчетов. Кроме того, необходимо учитывать, что в отдельных случаях в основе предела точности экстраполяции сигнала целесообразнее применять величину суммарной ошибки, накопленной к данному n-отсчету, без нормирования на номер рассматриваемого отсчета:
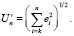(8)
Для определения данных зависимостей разработаны алгоритмы, блок-схемы которых представлены на рис. 1 и 2.
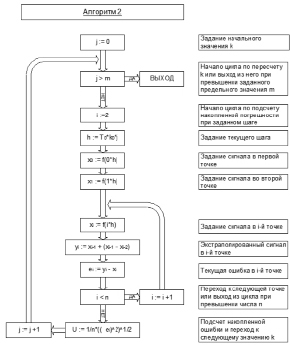
Рис. 2. Алгоритм определения зависимости накапливаемой ошибки от значения шага предсказания
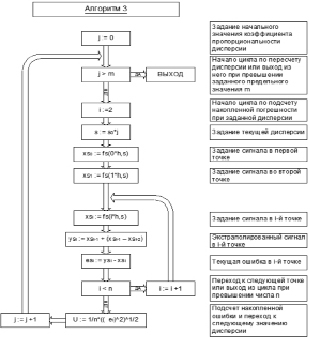
Рис. 3. Алгоритм для определения зависимости накапливаемой ошибки от случайной величины шума
Результаты исследования и их обсуждение
Рассмотрим модель предиктивного кодирования сигнала с наложением аддитивной помехи, являющуюся гауссовским случайным процессом с определенными параметрами. Реализация модели осуществлялась по заданной ниже схеме:
1) на основе аналогового шаблона S(t) создается тестовый базисный сигнал xsi;
2) задается случайный сигнал-помеха, являющийся гауссовским случайным процессом.
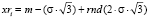, где rnd играет роль датчика случайных чисел;
3) реализовывается аддитивное накладывание шума на базисный тестовый сигнал
;
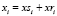4) осуществляется предиктивное кодирование при постоянном шаге предсказания.
Пример реализации предложенной схемы представлен программным модулем:
m = 0
σ = 0.2
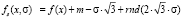– тестовый сигнал с шумом;
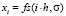– дискретизация сигнала с аддитивным шумом;
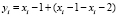– функция экстраполяции сигнала;
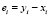– задание функции текущей ошибки.
Для определения зависимости ошибки предсказания от случайной величины наложения шума также был разработан алгоритм, блок-схема которого представлена на рис. 3.
Рассмотрим алгоритм предсказания сигнала при постоянном шаге, пример которого показан на рис. 4. В качестве примера взят сигнал S(t) = sin(t) + 0.5 sin(3t).
Как видно, метод предиктивного кодирования при постоянном шаге не всегда хорошо описывает исследуемые сигналы. Кроме того, погрешность одношагового предсказания существенно увеличивается, если сигнал включает шум.
Принцип разработанного алгоритма заключается в следующем. С определенной частотой осуществляется сопоставление текущей накапливаемой ошибки Un с установленным допустимым уровнем U*. Если накапливаемая ошибка не превосходит определенного разрешенного уровня Un < U*, то шаг кодирования h увеличивают в два раза по сравнению с начальным шагом h = 2h0. В противном случае шаг кодирования h уменьшают вдвое h = h0/2.
На основе разработанного алгоритма была осуществлена обработка того же сигнала. Для более наглядного сравнения эффективности алгоритма с адаптацией шага произведен одновременный вывод результатов обработки тестового сигнала двумя методами, представленный на рис. 5.
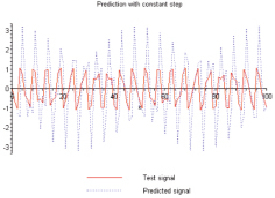
Рис. 4. Предсказание при постоянном шаге сигнала
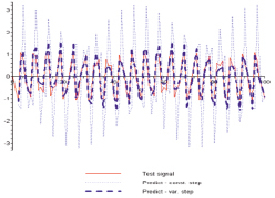
Рис. 5. Вывод результатов обработки сигнала двумя методами
Из последнего графика видно, что предсказание с адаптацией шага дает намного более близкий к реальности результат, чем предсказание с постоянным шагом (особенно в случае больших шагов дискретизации и предсказания).
Выводы
1. Исследован существующий алгоритм пошагового рекурсивного предсказания для разных типов сигнала (гармонического сигнала, суперпозиции гармоник, амплитудно-модулированного сигнала, меандра, сигнала с шумом), при этом анализу подвергнута зависимость накапливаемой ошибки от количества отсчетов.
2. Показано, что при увеличении числа отсчетов для всех рассмотренных тест-сигналов накопленная ошибка уменьшается, стремясь к некоторому стационарному значению, которое может рассматриваться как интегральная мера предсказуемости сигнала.
3. При анализе зависимости накапливаемой ошибки от значения шага экстраполяции установлено, что такие зависимости позволяют подбирать значение шага экстраполяции.
4. При добавлении к детерминированному сигналу шума накопленная ошибка предсказания при тех же параметрах экстраполяции (шага и число отсчетов) заметно возрастает и сильно зависит от дисперсии шума. Для зашумленного сигнала при уменьшении шага предсказания накопленная ошибка снижается в существенно меньшей степени, чем для детерминированного сигнала. Влияние величины дисперсии шума оказывается значительно более сильным. Разработаны алгоритмы адаптации шага. Наглядно продемонстрирована эффективность модифицированного алгоритма одношагового линейного предсказания сигнала по сравнению с существующим способом.
Библиографическая ссылка
Андреев К.В., Быков А.А., Киселева О.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРЕДИКТИВНОГО КОДИРОВАНИЯ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ, ОСНОВАННАЯ НА АЛГОРИТМЕ ИЗМЕНЯЮЩЕГОСЯ ШАГА КОДИРОВАНИЯ // Современные наукоемкие технологии. – 2020. – № 11-2. – С. 261-267;URL: https://top-technologies.ru/ru/article/view?id=38372 (дата обращения: 25.04.2024).