Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Морозов А.В. 1

---

1 ФГБОУ ВПО «Военно-космическая академия имени А.Ф. Можайского»

Основные математические модели теории колебаний имеют вид дифференциальных уравнений. Учитывая, что колебательные явления окружают нас повсюду, для полноценного инженерного образования необходимо ознакомление учащихся с рядом важнейших – эталонных математических моделей, описывающих основные типы колебательных явлений, среди которых есть уравнение Дуффинга. Современная математика накопила большой набор средств исследования таких моделей, причем для изучения конкретной модели можно применить два, три, а то и более методов, среди которых есть приближенные аналитические, а также методы численного исследования. Всесторонность (мы говорим – комплексность) изучения одной и той же модели разными методами, с нашей точки зрения, является действенным учебным приемом, усиливающим мотивацию учащихся к учебе, так как любое сравнение результатов вызывает у студентов естественный интерес, они получают энергетические импульсы к дальнейшим действиям, параллельно формируются исследовательские навыки. В настоящей статье на примере одного частного вопроса механики предлагается комплексный подход к его изучению. Важно, чтобы методологическая схема обучения включала понятия физической и математической моделей, аналитических методов решения задачи, вычислительный эксперимент, сравнение результатов и совместное обсуждение.

Статья в формате PDF

0 KB

мотивация к учебе

комплексный подход к решению задачи

теория колебаний

1. Морозов А.В. О компьютерном моделировании колебательных систем с одной степенью свободы на фазовой плоскости // Современные наукоемкие технологии. 2019. № 8. С. 147–152.

2. Морозов А.В., Бригаднов И.А. Компьютерное моделирование свободных колебаний в консервативных системах // Современные образовательные технологии в подготовке специалистов: cб. научных трудов Ш Всероссийской научной конференции (г. Санкт-Петербург, 5–6 марта 2020 г.). СПб.: Санкт-Петербургский горный университет, С. 319–323.

3. Панфилова А.П. Инновационные педагогические технологии. Активное обучение. М.: Изд. центр Академия, 2009. 192 с.

4. Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981. 356 с.

5. Алдошин Г.Т. Теория линейных и нелинейных колебаний. СПб.: Лань, 2013. 320 с.

6. Треногин В.А. Обыкновенные дифференциальные уравнения. М.: ФИЗМАТЛИТ, 2009. 312 с.

7. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: МЦНО, 2012. 343 с.

8. Дьяконов В.П. MATLAB. Полный самоучитель. М.: ДМК Пресс, 2012. 768 с.

9. Макаров Е.Г. Инженерные расчеты в Mathcad 15. СПб.: Питер, 2011. 400 с.

10. Булекбаев Д.А., Морозов А.В. Формирование и развитие навыков вычислительного эксперимента у обучающихся на примере исследования динамической системы // Труды Военно-космической академии им. А.Ф. Можайского. 2017. Вып. 656. С. 106–114.

В статье на примере одного частного вопроса механики обсуждается идея его изучения с разных ракурсов [1, 2]. На конкретной модели демонстрируются аналитические методы исследования, полученные результаты анализируются, а затем проводится моделирование системы с использованием ПК. Такая комплексность изучения вопроса преследует цель повысить мотивацию к познанию нового, ибо студент, осознавший даже не в полной мере результат применения одного метода, сравнивая его с результатом применения другого, если не увидит близости результатов, получит стимул разобраться в сути происходящего. Если же результаты будут близки, то возникнут так необходимые в обучении положительные эмоции. Таким образом, результат сравнения будет в любом случае толчком к активизации работы студента [3]. Кроме того, заметим, что компьютерные методы исследования математических моделей технических систем сегодня приобретают всё большее значение, а в инженерных кругах им часто отдается предпочтение. Обосновывается это тем, что ресурс времени для применения аналитических методов порой мал, результат исследований надо получить быстро, а набор инструментов численного моделирования сегодня большой. В этой связи естественным является и изменение образовательной парадигмы. Сегодня помимо традиционных курсов типа информатики, программирования, численных методов, компьютерных технологий компьютер участвует в учебном процессе очень многих дисциплин. При этом молодежь, видя рядом с собой знакомую ей среду – в данном случае ПК, охотно откликается и подключается к обучению. Если двадцать лет назад в курсе, например, механики изучались только аналитические методы и компьютер не участвовал, то сегодня, на наш взгляд, элементы компьютерного моделирования должны присутствовать и здесь [4, 5].

Цель настоящей статьи заключается в проектировании содержания примерной методологической схемы комплексного подхода к проведению занятия по теме «Свободные колебания в консервативной системе» в курсе механики. В центр обучения ставится одна математическая модель реального физического процесса. К ее исследованию применяются различные приёмы, результаты и методы, демонстрируются численные эксперименты.

Физическая и математическая модели и аналитические подходы к исследованию

Метод фазовой плоскости. Рассмотрим одно из эталонных уравнений классической механики: дифференциальное уравнение Дуффинга [2, 4, 5]:

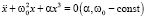. (1)

Оно описывает многие физические процессы, в частности движение грузика в среде без сопротивления по гладкой горизонтальной поверхности под действием упругой силы 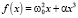(силу f(x) при α > 0 называют жесткой, при α < 0 – мягкой).

Запишем уравнение (1) в виде эквивалентной системы уравнений

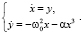(2)

Отсюда, деля второе уравнение на первое и интегрируя, легко находится первый интеграл системы, отражающий закон сохранения полной механической энергии

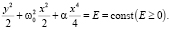(3)

Следующей, уже геометрической задачей является построение семейства алгебраических кривых на плоскости, отвечающих уравнению (3). На рис. 1 изображены инвариантные кривые системы (3), определяемые различными значениями энергии Е. Заметим, что в курсе аналитической геометрии построению семейств алгебраических кривых, зависящих от параметров (в данном случае α и E), уделяется, с нашей точки зрения, мало внимания, так что эта задача является актуальной.

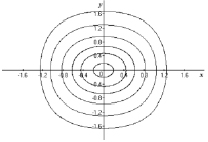
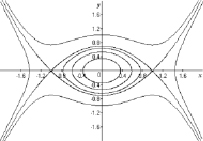
Рис. 1. Случай α > 0 – слева, α < 0 – справа

Видно, что как в случае жесткой, так и в случае мягкой характеристик f(x) уравнение (1) описывает колебательный процесс. Так как (3) представляет собой интегрируемое уравнение первого порядка 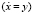, легко находится формула для периода колебаний

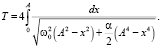(4)

Откуда вытекает главное свойство нелинейной системы – функциональная зависимость периода колебаний от амплитуды: T = T(A).

Эллиптические функции. Интегралы (4) вкладываются в более общий класс интегралов вида 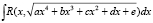. Здесь R – рациональная функция своих аргументов. Они называются эллиптическими и подробно были исследованы в середине XIX в. Суть построенной теории заключалась в том, что эти интегралы с помощью специальных замен приводились к стандартной форме. Для этих последних были разработаны специальные таблицы, позволяющие производить конкретные вычисления. Эллиптические интегралы и развитые на их основе эллиптические функции позволяют находить решения некоторого класса дифференциальных уравнений, среди которых и наше уравнение (1).

Замечание 1. Известно, что Леонард Эйлер определял экспоненциальную функцию x = e^t как решение задачи 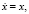x(0) = 1 в виде степенного ряда 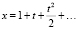. Тригонометрические функции x1 = cos t и x2 = sin t можно также определить как решения уравнения только уже второго порядка 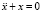, с начальными условиями: x(0) = 1 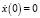и x(0) = 0, 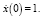Эллиптические функции x1 = sn(t, k), x2 = сn(t, k), x3 = dn(t, k), можно определить как компоненты решения дифференциальной системы уже третьего порядка с параметром k: 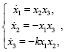удовлетворяющего условию x1(0) = 0, x2(0) = 1, x3(0) = 1, Легко видеть, что при k = 0 они переходят в тригонометрические. Таким образом, эллиптические функции являются обобщением тригонометрических, а следовательно, включаются в математический аппарат исследования колебательных процессов [6, 7].

К сожалению, теория эллиптических функций в настоящее время излагается во втузах в весьма урезанном виде. На наш взгляд, эту часть анализа игнорировать нельзя и надо вынести ее хотя бы на самостоятельную работу с последующим обсуждением на семинаре. Опуская ряд выкладок, приведем здесь вид общего решения уравнения (1), выраженного через эллиптический синус x = C sn(σ(t + h), k). Здесь константы C, σ, k выражаются через параметры α, ω₀, h – аддитивная постоянная [6].

В связи с формулой (4) приведем оценку величины T для жесткой характеристики:

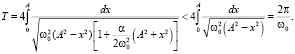
Таким образом, мы видим, что при α > 0 период T меньше 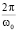– периода гармонического колебания. С другой стороны, можно показать, что при малых отрицательных σ T – возрастающая функция от амплитуды. Доказательство этого утверждения для уравнения (1), в частности, можно было бы провести с использованием эллиптических функций, о которых мы уже сказали, но здесь мы продемонстрируем иной подход, основанный на методе малого параметра – методе последовательных приближений.

Метод малого параметра. Не вдаваясь в подробности изложения метода малого параметра и ограничиваясь физическим уровнем строгости, выскажем его основную идею на примере нашего уравнения (1), предварив его следующим замечанием.

Замечание 2. Еще во времена И. Ньютона был известен метод нахождения решений дифференциальных уравнений в виде степенных рядов. В XVIII, XIX вв. на этой основе было исследовано много важных уравнений. Первые попытки нахождения периодических решений нелинейных уравнений типа (1) в виде рядов по параметру α x(t) = x0 + x1α + x2α² + ... были предприняты еще в середине XIX в., но не приводили к успеху, так как ряды включали так называемые секулярные (или резонансные) члены – члены вида tncoskt или tnsinkt, что вело к нахождению приближенных решений, но не периодических, а следовательно, определенных на ограниченном промежутке времени. Разгадка здесь заключалась в том, что в искомом решении частота колебаний также является неизвестной величиной, т.е. требует своего определения. Первыми на это обратили внимание Линштедт, Пуанкаре и Ляпунов, предложившие, примерно в одно и то же время различные модификации метода малого параметра [4].

Ясно, что при α = 0 все решения уравнения (1) периодические x0(t) = A sin(ω₀t + θ). Естественно ожидать, что для малых значений параметра α частота ω искомого решения должна быть близка ω₀ и зависеть от него, т.е. ω должна быть функцией параметра α. Учитывая это, положим

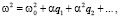(5)

где величины q1, q2, ... будем считать пока не определенными. Из (5) имеем

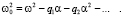(6)

Решение дифференциального уравнения (1) будем также искать в виде ряда

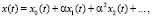(7)

с неизвестными функциями времени xi(t). Таким образом, алгоритм нашей задачи заключается в параллельном построении как неизвестной частоты (5), так и решения (7).

Подставим теперь ряды (6) и (7) в уравнение (1):

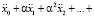
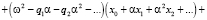(8)

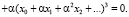
Уравнение (8), приводя подобные, запишем в эквивалентном виде

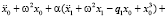
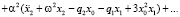
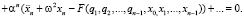
Откуда следует, что (7) будет частным решением уравнения (1) с начальными условиями x(0) = A, 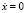(в начальный момент времени грузик отклонили и отпустили с нулевой скоростью), если функции x0(t), x1(t), x2(t), ... и неизвестные константы q1, q2, ... будут удовлетворять следующим уравнениям:

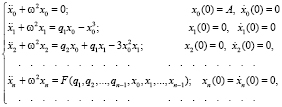(9)

Линейную систему (9) решают последовательно сверху вниз. Каждое уравнение, за исключением первого, является неоднородным. «Неоднородности» (т.е. правые части уравнений) включают неизвестные константы qk (k = 1, 2, …), выбором которых на каждом шаге исключают из правых частей резонансные члены. Естественно, что процедуру надо на каком-то шаге прервать и оценить погрешность полученного решения. Вопросы точности полученного таким образом решения мы здесь не обсуждаем, ограничиваясь физическим уровнем строгости. Отметим только, что они являются достаточно сложными и важными [4, 6, 7].

Ограничиваясь первыми двумя уравнениями в системе (9) и выбирая константу 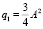, легко выводится, например, следующее приближенное решение уравнения (1):

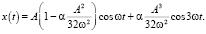(10)

И как уже отмечалось, параллельно с этим нашлась и частота 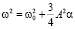, α « 1. Решению (10), как мы понимаем, отвечает колебание с амплитудой A и периода

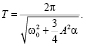(11)

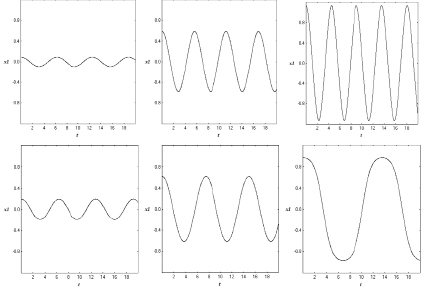
Рис. 2. Интегральные кривые (1) для α > 0 (первый ряд) и α < 0 (второй ряд)

Точность приведенного решения (формул (10), (11)) зависит от того, насколько параметр α мал. С ростом значения α точность формул (10) и (11) падает, но главное остается – их качественный смысл. В частности, из (11) видно, что при α > 0 период T – убывающая функция от A, при α < 0 – период T – возрастающая функция от A.

Компьютерное моделирование траекторий и решений

В статье [2] были приведены численные эксперименты, позволяющие визуализировать всё вышесказанное относительно монотонности периода T, исследуя систему (2) на фазовой плоскости. На эффект отсутствия изохронности в системе с кубической нелинейностью можно взглянуть и с другой стороны, если вывести на экран монитора интегральные кривые, используя какую-либо из вычислительных систем [8, 9]. На рис. 2 три верхних рисунка отвечают параметру α > 0, три нижних – параметру α < 0. В первом случае видно, что с ростом начального отклонения частота колебаний растет, во втором убывает.

В заключение этой части статьи для уравнения (1) приведем задания на самостоятельную работу, выполнение которых требует проведения вычислительного эксперимента на фазовой плоскости. Работа не потребует большого времени, но познавательный эффект будет значительным [10].

1. Пусть параметры ω₀ и α заданы (например, ω₀ = 1 и α = 1). Требуется определить амплитуду A колебания периода π ≈ 3,14.

2. Пусть параметр ω₀ задан (например, ω₀ = 1). Требуется определить α, при котором осциллятор будет иметь амплитуду колебания A = 2 периода T (например, T = 3,14).

3. Найти период T колебания осциллятора с параметрами 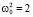и α = –1,5. если в начальный момент осциллятору в положении x(0) = 0 сообщить импульс 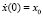. Какое значение x0 можно при этом взять?

4. Найти период T колебания осциллятора с параметрами 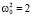, и α = –1,5, если в начальный момент осциллятору в положении x(0) = 0 сообщить импульс 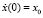. Какое значение x0 можно при этом взять?

Выводы

Учитывая, что мы живем в век постоянно изменяющихся технологий научных исследований, следует осуществлять постоянный поиск новых форм и методов обучения. Это касается, в частности, и фундаментальных основ технических дисциплин. Включение вычислительного практикума наряду с качественным анализом математических моделей, на наш взгляд, должно стимулировать у студентов интерес к фундаментальным знаниям. Обсуждаемый в настоящей статье вопрос в первую очередь затрагивает преподавателей технических дисциплин: механики, электротехники, радиотехники – т.е. там, где возникают колебательные явления. Сегодня персональный компьютер позволяет дополнить изложение многих классических результатов их визуализацией, что является целесообразным со всех точек зрения.

В статье мы спроектировали канву объёмного изучения одного из эталонных уравнений механики – Дуффинга. В качестве других эталонных (в смысле базовых, феноменологических) моделей можно было бы предложить уравнения автоколебаний Ван-дер-Поля или математического маятника. С нашей точки зрения, важным в формировании современного специалиста является комплексность интегрируемых в нем знаний: чтобы при решении конкретной задачи были применены несколько исследовательских методов, востребованы знания из разных дисциплин, присутствовал численный эксперимент, проведенный, возможно, в разных программных средах и сравнительный анализ полученных результатов.

Библиографическая ссылка