Большинство устройств в своем составе имеют передаточные механизмы, которые включают в себя механические передачи. Разновидностью механических передач являются зубчатые передачи. Существует большое количество различных вариантов зубчатых передач [1]. Наиболее распространенными являются прямозубые и косозубые цилиндрические зубчатые передачи. Причем нагрузочная способность у косозубых передач по сравнению с прямозубыми выше вследствие наклона зуба и увеличения длин контактных линий при одинаковой ширине колес. Такие передачи применяются как в понижающих частоту вращения (редукторы), так и в повышающих (мультипликаторы) механизмах. Зачастую боковая поверхность зубьев выполнена по эвольвенте, а зубья имеют плоскость симметрии. В механизме, который содержит одну передачу, состоящую из малого колеса (шестерни) и большого колеса, можно менять не только направление вращения ведущего колеса, но также менять направление потока мощности от малого к большому колесу и наоборот. Основными преимуществами таких передач являются: высокий КПД (до 98 %); большой диапазон передаваемых скоростей (до 150 м/с) и мощностей (до десятков тысяч кВт); надежность и долговечность (до 30 000 ч). С учётом того, что обслуживание этих передач простое, есть у них и недостатки: необходимость высокой точности изготовления и монтажа, особенно у широких колес при небольших диаметрах, а также возникающий шум при работе со значительными скоростями. Несмотря на это зубчатые цилиндрические передачи получили широкое распространение во всех отраслях промышленности: в автомобилестроении, судостроении, авиастроении, в технологическом оборудовании тяжелой и легкой промышленности и прочее.
Одним из распространенных недорогих материалов, применяемых для изготовления зубчатых колес, который обладает достаточной прочностью, является конструкционная сталь. По условию работы одно из колес пары, как правило большее, делается менее твердым, в среднем на (10…15) НВ, чтобы передача имела возможность приработаться. В передаче наиболее нагруженным считается меньшее колесо (шестерня). Зачастую шестерню выполняют заодно с валом (в большинстве случаев это экономически оправдано), и такой узел носит название вал-шестерня.
Зубчатые колеса изготовляются согласно технологическому процессу, в основе которого находится конструкторская документация. В отличие от простых изделий, при разработке конструкции колеса или более сложного узла – вала-шестерни необходимо руководствоваться различными стандартами, в которых приведены: расчет геометрии, расчет статической прочности и усталостной выносливости, нормы точности и плавности работы, различные технические требования. Учесть все требования при проектировании задача непростая, конструктору необходимо иметь соответствующий опыт. Для облегчения труда конструктора при разработке документации используют CAD системы от «легких» до «тяжелых», например Компас-3D, T-Flex CAD [2], SolidWorks и др. Некоторые CAD системы содержат модули CAE и позволяют производить весь комплекс необходимых расчётов и получать готовую конструкторскую документацию.
Оценка прочности является одним из этапов конструирования колес цилиндрической передачи. Недостаточная прочность колес в передаче может привести к быстрому выходу из строя механизма вследствие его поломок, что в свою очередь снижает надежность узла и повышает стоимость его эксплуатации. Например, если колеса в передаче не будут удовлетворять статической прочности, то уже на этапе пуска машины из-за перегрузок могут возникнуть трещины или поломки зубьев. Известно, что при передаче вращения по контактным линиям нормально к боковым поверхностям контактирующих зубьев действуют усилия, причём от действия усилий возникают контактные напряжения, а основание зубьев подвергается изгибу с возникновением соответствующих напряжений.
Существуют различные методы определения прочности [1, 3, 4]. В статье [5] произведена оценка прочности прямозубой шестерни (сталь 20ХН3А) тягового редуктора локомотива в SolidWorks Simulation с выделением площадки контакта на боковой поверхности для момента трогания локомотива с места с определением напряжений по критерию Мизеса, причем для построения 3D модели использована программа Компас. В статье [6] для косозубой шестерни планетарного редуктора проведен анализ прочности по критерию Мизеса и других параметров в квазистатических условиях с использованием пакета BETA CAE Systems. Большинство авторов [7–9] используют в своих работах ANSYS для оценки прочности зубчатых передач и ее элементов. Есть специальные продукты для оценки прочности на основе стандартов ISO, DIN, AGMA, VDI и т.д., одним из таких является KISSsoft [10]. Использование СAD/CAE программ для моделирования деталей и узлов с дальнейшим анализом прочности и др. параметров является современным методом и актуальным решением сложных производственных задач.
Цель исследования: с помощью модуля T-Flex CAD Анализ, встроенного в учебную версию программы T-Flex CAD, провести определение напряженно-деформированного состояния вала-шестерни как объемной конструкции с учётом пространственного приложения усилий с оценкой статической прочности по эквивалентным напряжениям.
Материалы и методы исследования
Метод, положенный в основу исследования, приведен в литературе [3], в его основе рассматривается зацепление зубьев как сжатие двух цилиндров (рис. 1) с радиусами кривизны рабочих поверхностей ρ1 и ρ2 под действием удельной нормальной силы ω = Fn/l∑ по площадке шириной в среднем равной по величине 2а, которая использована автором при построении контактных линий на боковых поверхностях зубьев шестерни.
Для оценки параметров зацепления с целью построения 3D модели вала-шестерни использована программа [11]. Вал-шестерня (рис. 2) включает в себя косозубую цилиндрическую шестерню с внешним зацеплением и левым наклоном зубьев из стали марки 50 с пределом текучести σт = 530 МПа, модуль упругости первого рода E = 2,16•105 МПа, коэффициент Пуассона μ = 0,3. Зацепление имеет следующие параметры: модуль mn = 4 мм; число зубьев шестерни z1 = 24 шт. и колеса z2 = 98 шт.; ширина шестерни bw = 104 мм; угол наклона зубьев β = 12,578 °; межосевое расстояние aw = 250 мм; коэффициент торцевого перекрытия εα = 1,67; окружное усилие в зацеплении Ft = 10627 Н.
В зацеплении косозубых зубчатых колес, вследствие наклона зубьев под некоторым углом β, как правило, находятся две или три пары контактирующих зубьев. В источнике [3] установлено, что если в зацеплении находятся две пары взаимодействующих зубьев, то полное усилие распределяется в следующем соотношении: 58 % на первую пару и 42 % на вторую пару зубьев. В статье рассматривается такое зацепление зубьев, при котором фактически в зоне контакта находятся три пары зубьев (рис. 3).
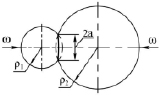
Рис. 1. Графическое представление метода, положенного в основу исследования
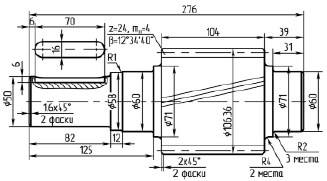
Рис. 2. Эскиз вала-шестерни
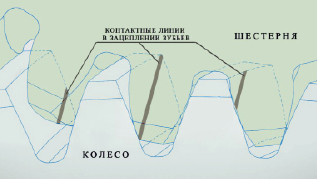
Рис. 3. Распределение контактных линий в зацеплении зубьев
По данным в источниках [1, 3, 4] использованы формулы (1–3) в расчётах.
Полное нормальное усилие:
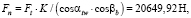 (1)
(1)
где K = KА•KHα•KHβ•KHV – коэффициент расчетной нагрузки, K = 1,845 согласно [4], sin βb = = sin β•cos α, αtw и α [1, 3, 4].
Полуширина плоскости контакта:
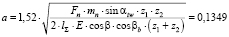 мм. (2)
мм. (2)
Средняя суммарная длина контактных линий в зацеплении (рис. 3)
lΣ = bw•εα/cos β = 171,106 мм. (3)
В исследовании напряженно-деформированного состояния вала-шестерни приняты допущения: на шестерню со стороны колеса действует полное нормальное усилие, определяемое по формуле (1), по выделенным площадкам контакта взаимодействующих зубьев (рис. 4); из-за небольших ограничений используемой версии T-Flex CAD Анализ [12] закрепление вала-шестерни осуществляется по цапфам вала с определением статической прочности по эквивалентным напряжениям прямым методом. Первая пара взаимодействующих зубьев с контактной линией lΣ1 = 99,548 мм входит в зацепление по всей ширине зубьев колеса, так как ширина шестерни на 4 мм больше колеса, причем усилие в паре составляет 58,18 % от Fn и равно 12014,12 Н. Вторая пара взаимодействующих зубьев с длиной контактной линии lΣ2 = 40,855 мм входит в зацепление в области головки зубьев шестерни, при этом усилие в паре составляет 23,88 % от Fn и равно 4931,2 Н. Третья пара взаимодействующих зубьев с длиной контактной линии lΣ3 = 30,703 мм входит в зацепление в области ножки зубьев шестерни, причем усилие в паре составляет 17,94 % от Fn и равно 3704,6 Н (рис. 4).
Контактное напряжение в полюсе зацепления без учета дополнительных нагрузок (динамических и от неравномерности распределения усилий, то есть при K = 1) согласно [4]:
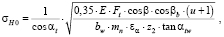 (4)
(4)
где tan αt = tan α/cos β.
Также контактное напряжение в полюсе зацепления при K ≠ 1:
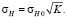 (5)
(5)
Максимальные контактные напряжения в зоне контакта взаимодействующих профилей зубьев колес согласно данным источника [3]:
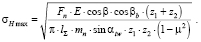 (6)
(6)
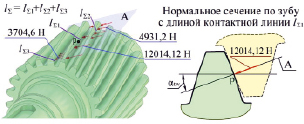
Рис. 4. Фактическое распределение контактных линий и полного нормального усилия, действующего в плоскости зацепления А
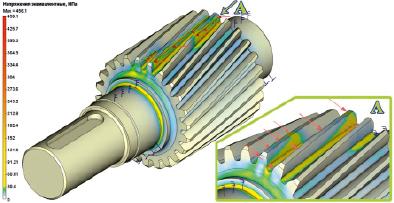
Рис. 5. Картина эквивалентных напряжений в шестерне детали вал-шестерня
Результаты исследования и их обсуждение
На основе объёмной конструкции вала-шестерни, твердотельная модель которого была построена в программе T-Flex CAD, произведено определение напряженно-деформированного состояния с учётом пространственного приложения усилий в модуле T-Flex CAD Анализ. В результате расчета определялась статическая прочность шестерни по относительным эквивалентным напряжениям (рис. 5), которые вычислялись в программе согласно IV теории прочности. Произведена оценка запаса прочности по рассчитанным напряжениям относительно допускаемых напряжений – это напряжения предела текучести для выбранного материала.
Общий запас статической прочности шестерни составил 1,162, что больше минимально допустимого 1,1. Максимальные эквивалентные напряжения при расчете статической прочности вала-шестерни в зоне взаимодействующих зубьев шестерни составили σэкв = 456,1 МПа. Так при расчете сопряженного колеса, то есть большего по размеру, имеющего сплошное поперечное сечение с диаметром вершин 409,64 мм и шириной 100 мм, эквивалентные напряжения составили σэкв = 367,6 МПа, что на 24 % меньше, чем у шестерни. Контактное напряжение в полюсе зацепления при K = 1, формула (4), равно 419,41 МПа, а при K = 1,845 формула (5) имеет такой же порядок, что и максимальные контактные напряжения, рассчитанные по формуле (6), которые равны 568,74 МПа.
Заключение
Значения эквивалентных напряжений, полученных при определении напряженно-деформированного состояния шестерни, как элемента вала-шестерни, с учетом пространственного приложения усилий не превышают значений напряжений предела текучести и напряжений, которые определены стандартными методами. Отличие эквивалентных напряжений от максимальных контактных напряжений составляет 25 %. Получено, что шестерня является более нагруженной, чем колесо. Рассматривая распределение напряжений по торцевым поверхностям взаимодействующих зубьев шестерни, можно увидеть, что по величине они меньше, чем в зоне контакта, это объясняется тем, что шестерня имеет выступ относительно колеса на 2 мм с каждой стороны, а это в свою очередь уменьшает риск разрушения кромок зубьев у торца шестерни. При моделировании принимались идеализирующие условия работы, а при эксплуатации возникают деформации вала, перекос осей, возможны неточности изготовления и монтажа, что приводит к изменению площадки контакта и увеличению величины напряжений. Также ограничения используемой версии программы не позволяют провести полный расчет зацепления с учетом всех факторов, влияющих на зацепление, но, применяя такой метод оценки прочности, можно на этапе проектного расчета и конструирования узла оценить его статическую прочность с целью исключения ошибок проектирования и снижения затрат опытно-конструкторских работ.
Библиографическая ссылка
Иващенко А.П. ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ ПРОЧНОСТИ ШЕСТЕРНИ, ВХОДЯЩЕЙ В СОСТАВ ВАЛА-ШЕСТЕРНИ // Современные наукоемкие технологии. 2020. № 11-1. С. 31-36;URL: https://top-technologies.ru/ru/article/view?id=38334 (дата обращения: 01.01.2026).
DOI: https://doi.org/10.17513/snt.38334



