При касании боковых профилей контактирующих зубьев в зубчатой передаче происходит передача вращения. Между сопряженными зубьями на шестерне возникает активная сила давления, а на колесе – сила сопротивления. Ножка зуба от действия нагрузки подвергается деформации изгиба, а на боковой поверхности зубьев действует мгновенно линейный контакт, причем линия контакта перемещается по этим поверхностям, при этом изгиб у основания ножки проявляется до тех пор, пока сопряженные зубья не выйдут из зацепления. На боковых поверхностях зубьев, которые находятся в зацеплении, действуют контактные напряжения, а у основания ножки зуба – напряжения изгиба. Сопряженные зубья находятся в сложном напряженно-деформированном состоянии [1].
На сегодняшний день рабочую конструкторскую документацию зачастую разрабатывают, применяя CAD программы, например T-Flex CAD [2]. Сначала строят трехмерную твердотельную модель изделия, например, косозубого цилиндрического колеса зубчатого, потом получают ассоциативные чертежи и другую документацию.
На одном из этапов проектирования механизмов технологического оборудования оценивают работоспособность узла механизма, например зубчатой передачи или ее элемента – зубчатого колеса, по критериям прочности. Рекомендуемую оценку прочности зубчатых передач, как правило, выполняют по методикам в источниках [1, 3, 4], но можно производить оценку прочности передач другими методами. Так, в литературе [5] приведена упрощенная методика оценки прочности зубчатых передач с помощью приложения Simulation системы I-DEAS NX – инструмента для виртуального моделирования и проведения инженерных расчетов. В литературе [6, 7] используют программу ANSYS для проведения прочностных расчетов зубчатых передач, а в источнике [8] для оценки прочности зубчатых передач и механизма в целом используют программу SolidWorks Simulation.
Применяя интегрированный в CAD программу модуль конечно-элементных расчетов, можно выполнять математическое моделирование распространенных физических явлений, находить правильное решение задач, возникающих при проектировании изделий [9]. Такие интегрированные модули расчетов актуальны из-за сокращения общих затрат на поиск достоверного решения при разработке дорогостоящего технологического оборудования. Таким образом, используя такой модуль при исследовании прочности косозубого цилиндрического колеса зубчатого, можно получить ассоциативную связь между трехмерной и конечно-элементной моделями, а также чертежом колеса зубчатого, что позволяет разрабатывать рациональные конструкции передач в механизмах технологического оборудования на проектном этапе.
Цель исследования: по построенной трехмерной модели большего по размеру косозубого цилиндрического колеса зубчатого из двух в передаче механизма технологического оборудования, используя модуль T-Flex CAD Анализ, провести исследование статической прочности с определением эквивалентных напряжений и запаса прочности в сравнении с рекомендуемыми методиками оценки усталостной прочности [3, 4].
Материалы и методы исследования
С помощью программы «Расчет цилиндрических зубчатых передач в среде Microsoft Office» [10] получены геометрические параметры для построения трехмерной модели большего по размеру зубчатого колеса из двух в передаче (табл. 1, рис. 1).
Таблица 1
Параметры зубчатой передачи, принятой в расчет
|
Наименование параметра |
Параметр |
|
Тип зубчатой передачи |
Цилиндрическая внешнего зацепления косозубая без смещения |
|
Материал большего по размеру зубчатого колеса из двух в передаче |
Сталь 50, σт = 450 МПа |
|
Межосевое расстояние, aw , мм |
250 |
|
Модуль в нормальном сечении, mn , мм |
4 |
|
Угол наклона зубьев, β ° |
12,578 |
|
Направление линии зуба |
вправо |
|
Коэффициент торцового перекрытия, εα |
1,67 |
|
Число зубьев шестерни/колеса, z1 / z2 , шт. |
24 / 98 |
|
Ширина колеса, bw , мм |
100 |
|
Окружное усилие в зацеплении, Ft , Н |
10267 |
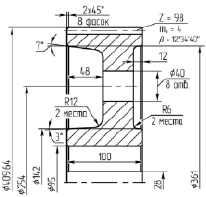
Рис. 1. Эскиз косозубого цилиндрического колеса зубчатого
Боковая поверхность контактирующих зубьев, находящихся в зацеплении, подвергается местной деформации. В источнике [4] для упрощения аналитических расчетов контактной прочности зубьев рассматривается сжатие двух цилиндров (рис. 2) по площадке, которая из-за переменной жесткости зубьев по длине контактной линии имеет разную ширину, но в среднем величиной 2а. В статье при построении контактной линии на боковых поверхностях зубьев колеса выделена площадка шириной 2а.
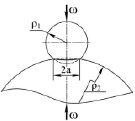
Рис. 2. Модель пары зубьев, принятая в расчет
Используя формулы (1)–(5), приведенные в источниках [1, 3, 4], определены параметры, необходимые для подготовки твердотельной модели косозубого цилиндрического колеса зубчатого к статическому расчету на прочность.
Приведенный радиус кривизны рабочих поверхностей для передачи с внешним зацеплением определяется по формуле
ρпр = 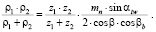 (1)
(1)
С учетом того, что колеса без смещения, получаем ρпр = 14,102 мм.
Колесо и шестерня изготовлены из одинакового материала, работают при одинаковых условиях, поэтому принимаем модуль упругости первого рода E = 2,16?105 МПа, коэффициент Пуассона μ = 0,3 [4].
Полуширина плоскости контакта определяется по формуле
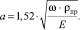 (2)
(2)
Удельная нормальная сила определяется по формуле
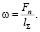 (3)
(3)
Полуширина плоскости контакта a = 0,1349 мм. Полная ширина плоскости контакта 2a = 0,2698 мм.
Средняя суммарная длина контактных линий в зацеплении, которая приходится на все зубья, одновременно находящиеся в зацеплении
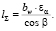 (4)
(4)
Получаем lΣ = 171,106 мм.
При расчете косозубого цилиндрического колеса зубчатого введены допущения: нагрузка в зацеплении заменяется полным нормальным усилием с учетом коэффициента расчетной нагрузки, формула (5); в зацеплении участвуют три пары контактирующих зубьев, так что средняя суммарная длина контактных линий в зацеплении находится в пределах расчетных величин; на контактирующих боковых поверхностях зубьев колеса выделены контактные площадки; фиксация колеса при расчете производится по отверстию под вал и по рабочим поверхностям паза шпоночного.
Согласно допущениям на трех зубьях колеса выделены контактные линии. Первая пара зубьев с контактной линией lΣ1 зацепляется по всей длине зубьев, причем вторая и третья пары зубьев с длинами контактных линий lΣ2 и lΣ3 зацепляются в области головки и ножки зубьев соответственно. Измерив контактные линии на трехмерной модели (рис. 3), получены фактические длины: первой пары зубьев lΣ1 = 99,548 мм; второй – lΣ2 = 40,855 мм; третьей – lΣ3 = 30,703 мм. Суммарная длина контактных линий lΣ = lΣ1 + lΣ2 + lΣ3.
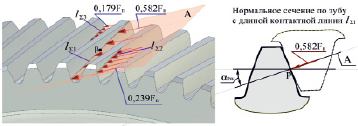
Рис. 3. Контактные линии и усилия на рабочих поверхностях колеса зубчатого
Полное нормальное усилие определяется по формуле
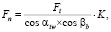 (5)
(5)
где K = KА?KHα?KHβ?KHV – коэффициент расчетной нагрузки, принимается равным K = 1,845 [4], αtw и α по [11].
Контактные линии в косозубом зацеплении расположены под углом βb, который является основным углом наклона зубьев sin βb = sin β?cos α.
Получаем Fn = 20649,92 Н, а удельная нормальная сила ω = 120,685 Н/мм.
Полное нормальное усилие в зацеплении двух контактирующих пар зубьев распределяется в соотношении 58 % на первую пару и 42 % на вторую пару зубьев [4].
С учетом допущений в расчетной модели находятся три пары зубьев в зацеплении, следовательно, нагрузка в 42 % распределяется между второй и третьей парами зубьев (табл. 2). Сравнивая первый и последний столбцы в табл. 2, можно увидеть хорошую корреляцию данных.
Таблица 2
Полное нормальное усилие
|
Fn по [4] |
Fn = 20649,92 Н в расчетной модели |
Fn в расчетной модели |
|||
|
1 пара |
58 % |
1 пара – 12014,12 Н |
1 пара – 58,18 % |
||
|
2 пара |
42 % |
2 и 3 пары – 8635,80 Н |
2 пара – 4931,20 Н |
2 и 3 пары – 41,82 % |
2 пара – 23,88 % |
|
3 пара – 3704,60 Н |
3 пара – 17,94 % |
||||
В приложении 1 к ГОСТ 21354-87 [3] контактное напряжение в полюсе зацепления вычисляется по формуле
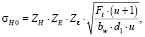 (6)
(6)
где
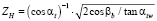 ;
;
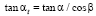 ;
; 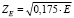 ;
;
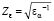 ; u = z2/z1; d1 = mn?z1/cos β;
; u = z2/z1; d1 = mn?z1/cos β;
остальные данные приведены в табл. 1.
В [4] приводится формула максимальных контактных напряжений при контакте рабочих профилей зубьев колес, изготовленных из одинакового материала
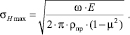 (7)
(7)
Результаты исследования и их обсуждение
На основе данных, представленных выше, и с помощью интегрированной в CAD программу среды T-Flex CAD Анализ проведено исследование на статическую прочность большего косозубого цилиндрического колеса зубчатого из двух колес в передаче механизма технологического оборудования. Определены относительные эквивалентные напряжения, вычисляемые из компонентов тензора напряжений согласно IV теории прочности [9]. Определен коэффициент запаса прочности по эквивалентным напряжениям, то есть отношение допускаемых напряжений материала к эквивалентным напряжениям, где в качестве допускаемого напряжения для пластичных материалов выбран предел текучести (табл. 1). Согласно расчетам на рис. 4 показано распределение относительных эквивалентных напряжений в косозубом цилиндрическом колесе зубчатом.
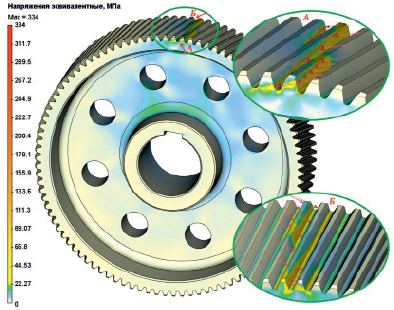
Рис. 4. Распределение эквивалентных напряжений в косозубом цилиндрическом колесе зубчатом
Таблица 3
Напряжения в области контакта сопряженных поверхностей зубьев
|
Метод исследования |
Вид напряжений |
Обозначение |
Величина, МПа |
|
Исследование статической прочности в T-Flex CAD Анализ |
Относительные эквивалентные напряжения |
σэкв |
334,00 для колеса на рис. 4 |
|
367,60 для колеса на рис. 5 |
|||
|
Оценка напряжений по ГОСТ 21354-87 [3] |
Контактное напряжение в полюсе зацепления |
σH0 |
419,41 |
|
Оценка напряжений по [4] |
Максимальные контактные напряжения |
σHmax |
568,74 |
Определена статическая прочность рассчитываемого колеса зубчатого в T-Flex Анализ получен запас прочности равный SHрасч. = 1,34.
Согласно [3] минимальный запас прочности для зубчатых колес, изготовленных из однородного материала, равен SHmin = 1,1.
Для сравнения напряжений, полученных на рис. 4, построена другая модель косозубого цилиндрического колеса зубчатого (рис. 5) по параметрам зацепления (табл. 1, 2) и определены эквивалентные напряжения. Результаты представлены в табл. 3 и на рис. 5. Также в табл. 3 приведены расчеты напряжений по формулам (6) и (7). В колесе, которое имеет диск с равномерно расположенными в нем отверстиями (рис. 4) имеет меньшие по значению эквивалентные напряжения, чем колесо, представленное на рис. 5. Это объясняется тем, что уменьшается жесткость колеса, а напряжения перераспределяются, тем самым происходит понижение порядка напряжений. Так, колесо на рис. 4 имеет максимальные перемещения в зоне нагрузки 0,0218 мм, а колесо на рис. 5 – 0,0121 мм, что на 44,4 % меньше. При этом масса колеса на рис. 5 больше на 45 %, чем колеса на рис. 4, что негативно сказывается не только на его моменте инерции при вращении, но и на себестоимости материала, а это делает колесо на рис. 5 зачастую экономически нецелесообразным в серийном производстве механизмов технологического оборудования, хотя по конструкции оно более простое.
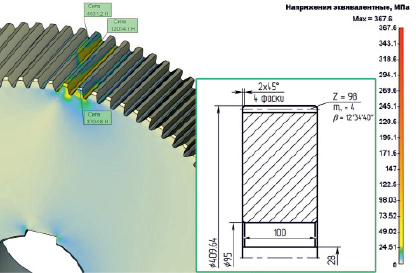
Рис. 5. Эскиз косозубого колеса зубчатого с распределением напряжений
Заключение
Рассчитанное косозубое цилиндрическое колесо зубчатое обладает запасом статической прочности под действием полного нормального усилия, причем усилие действует на три зуба, в том числе на зуб с длиной контактной линии lΣ1 приходится 58,18 % от общего усилия. Эквивалентные напряжения в среднем на 30 % меньше значений напряжения предела текучести и более чем на 50 % меньше расчетных величин максимальных контактных напряжений. Проведенное исследование колеса зубчатого имеет хорошую корреляцию с рекомендуемыми расчетными методами [3–5]. Такой метод исследования позволяет произвести оценку статической прочности конструируемого колеса зубчатого, а в целом и передачи, как части механизма технологического оборудования, что позволяет на предварительном этапе конструирования, то есть до расчета на усталостную выносливость и получения рабочих чертежей, подобрать рациональную конструкцию колеса и улучшить параметры проектируемого оборудования.
Библиографическая ссылка
Иващенко А.П. ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ ПРОЧНОСТИ КОСОЗУБОГО ЦИЛИНДРИЧЕСКОГО ЗУБЧАТОГО КОЛЕСА // Современные наукоемкие технологии. 2020. № 10. С. 51-56;URL: https://top-technologies.ru/ru/article/view?id=38254 (дата обращения: 04.02.2026).
DOI: https://doi.org/10.17513/snt.38254



