Важной частью ступени паровой турбины является диафрагменное уплотнение, служащее для уменьшения протечки пара в радиальном зазоре между цилиндрической поверхностью вала и внутренней расточкой диафрагмы.
К диафрагменным уплотнениям предъявляется ряд требований по надежности:
- обеспечение минимальной протечки пара;
- простота и ремонтопригодность кон- струкции;
- обеспечение надежности работы бесконтактного уплотнения при возможном выборе радиального зазора между поверхностью вала турбины и диафрагмой;
– обеспечение надежности работы уплотнения при допустимом осевом смещении ротора турбины относительно статора.
В современных конструкциях турбин большое распространение получили диафрагменные лабиринтные уплотнения, как наиболее полно соответствующие вышеперечисленным требованиям. Типичная конструкция диафрагменных уплотнений паровых турбин средней и большой мощности представлена на рис. 1.
На нижней расточке диафрагмы закрепляются подпружиненные сегменты обоймы, на внутреннюю поверхность которых запрессовывается металлическая лента, образующая несколько кольцевых гребней (усиков). На ответной поверхности вала турбины делаются под гребни канавки и выступы. Между гребнями и проточками на валу турбины образуются вихревые камеры. Радиальный зазор между гребнями уплотнения и поверхностью вала обычно составляет δ = 0,4–0,5 мм.
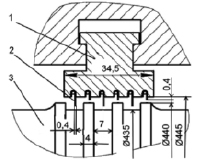
Рис. 1. Диафрагменное уплотнение паровой турбины: 1 – сегмент обоймы диафрагменного уплотнения; 2 – усики; 3 – вал турбины
При имеющемся перепаде давления на уплотнение пар проходит через узкие щели под каждым гребнем, его потенциальная энергия преобразуется в кинетическую энергию, которая, в свою очередь, преобразуется в тепло за счет гашения скорости трением. Этот процесс повторяется от гребня к гребню, в результате чего давление пара вдоль лабиринта падает и, следовательно, уменьшается протечка пара через уплотнение.
На пусковых и переходных режимах работы паровой турбины наблюдается осевое смещение ротора относительно статора. Это объясняется неравномерным температурным расширением при прогреве или охлаждении массивного статора турбины и относительно легкого ротора. Величина относительного осевого смещения ротор-статор в паровых турбинах может достигать ±1,5–2,5 мм [1–3]. При этом происходит изменение положения усиков лабиринтного уплотнения относительно проточек на валу ротора турбины. Изменение размера вихревых камер, относительно их номинальных размеров, приводит к изменению протечки пара через диафрагменные уплотнения, что влияет на эффективность ступеней и величину осевого усилия, воспринимаемого упорным подшипником турбины.
Известны нормативные методики расчета утечки пара через лабиринтные уплотнения [4, 5]. Однако они позволяют рассчитать расход пара через лабиринтное уплотнение лишь при некотором номинальном (обычно среднем) расположении гребней относительно проточек на валу. Определить утечку пара при любом возможном положении гребней относительно проточек возможно предлагаемым далее методом. Методика основана на численном методе CFD.
Цель исследования заключается в исследовании влияния осевого смещения ротора паровой турбины на величину протечки пара через диафрагменное уплотнение ступени методами численного эксперимента. Это требует корректного выбора расчетной математической модели, включающей в себя расчетные уравнения и 3D-модель диафрагменного лабиринтного уплотнения. Для этого использовалась известная система уравнений движения вязкой жидкости.
Особенности расчетной модели
Численная математическая модель течения сжимаемого вязкого газа (водяного пара), использованная в расчетах, строится на классических уравнениях сохранения массы, импульса и энергии.
Уравнения в Декартовых координатах:
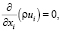
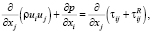
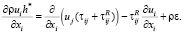
Здесь:
u – скорость потока;
p – статическое давление газа;
ρ – плотность газа;
i, j = 1, 2, 3 – номера осей координат (x, y, z);
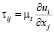– тензор касательных напряжений для осей i, j;
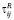– тензор напряжений Рейнольдса для осей i, j;
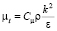– турбулентная вязкость в k-ε модели турбулентности;
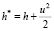– энтальпия потока пара по параметрам торможения.
Особенностями конструкции диафрагменных уплотнений паровой турбины является большой диаметр вала турбины под уплотнением (D ≈ 440 мм) и различие на порядок характерных геометрических размеров в уплотнении – радиального зазора (δ ≈ 0,5 мм) и ширины вихревых камер (≈ 4–6 мм). Это обуславливает необходимость чрезмерно большого числа расчетных ячеек в модели при пространственном 3D-моделировании, что требует больших вычислительных ресурсов. Однако осесимметричная конструкция диафрагменного уплотнения и большой радиус кривизны гребней позволяют использовать квазидвумерную модель, что и реализовано в предлагаемой методике.
На рис. 2 приведена расчетная модель рассмотренного диафрагменного уплотнения. На рисунке показано номинальное положение гребней уплотнения относительно проточек на валу и направление положительного смещения ротора относительно неподвижных элементов конструкции уплотнения.
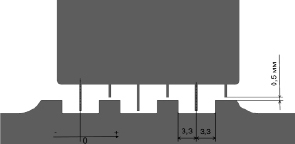
Рис. 2. Расчетная модель диафрагменного уплотнения паровой турбины
Густота расчетной сетки при моделировании выбиралась исходя из условия достижения сходимости по величине утечки пара с точностью до 1 %
Была выявлена большая чувствительность результатов расчета к густоте расчетной сетки в вихревых камерах и особенно в районе радиального зазора под гребнем уплотнения. Фрагмент конечного варианта расчетной сетки под гребнем уплотнения, обеспечивший требуемую сходимость, приведен на рис. 3.
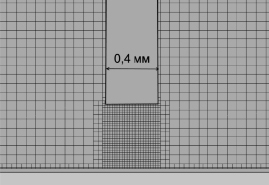
Рис. 3. Фрагмент расчетной сетки в области радиального зазора под гребнем диафрагменного уплотнения
На расчетную модель накладывались граничные условия, приведенные на рис. 4. Параметры пара выбирались характерными для первых ступеней паровых турбин средней мощности: давление пара на входе в ступень принято p1 = 5,4 МПа, температура t1 = 500 °С. Давление на выходе из ступени задавалось исходя из общего перепада давления на уплотнении: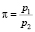 
= 1,25–2,0.
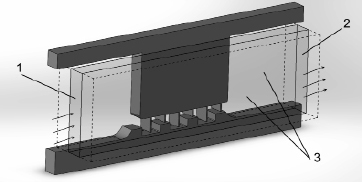
Рис. 4. Граничные условия на модели уплотнения: 1 – условие входа (статическое давление и температура пара); 2 – статическое давление пара на выходе; 3 – граничное условие симметрии
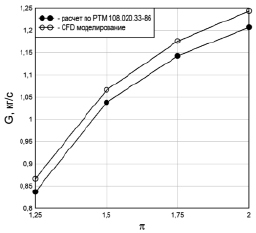
Рис. 5. Расход пара через диафрагменное уплотнение в зависимости от перепада давления на диафрагму
Для верификации расчетной модели выполнено сравнение полученных при численном моделировании данных с результатами, полученными при использовании нормативных расчетных методик [5]. Сравнение результатов, полученных указанными методами, при симметричном расположении гребней уплотнения относительно проточек ротора представлено на рис. 5.
Результаты, полученные с помощью CFD моделирования, отличаются от данных, полученных с помощью нормативных расчетных методик, на величину менее 3,5 %, что позволяет сделать вывод об адекватности использованной расчетной модели.
Результаты моделирования
Полученная в результате CFD моделирования графическая зависимость протечек пара через рассмотренное диафрагменное уплотнение ступени паровой турбины от осевого смещения ротора и перепада давления на уплотнение представлена на рис. 6.
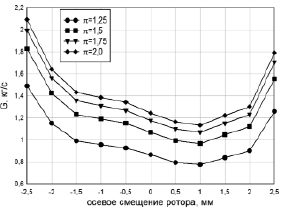
Рис. 6. Влияние осевого смещения ротора турбины на величину протечек пара через диафрагменное уплотнение
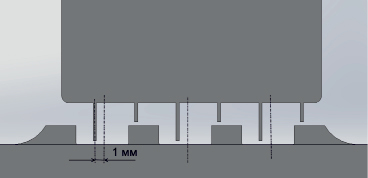
Рис. 7. Положение гребней уплотнения, обеспечивающее минимальные протечки пара через уплотнение
Установлено значительное влияние осевого смещения ротора турбина на величину протечек пара через уплотнение. Минимальное значение протечек пара достигается при несимметричном положении гребня уплотнения относительно торцевых поверхностей проточки на валу турбины.
Положение гребней уплотнения, обеспечивающее минимальный расход через уплотнение, показано на рис. 7. При этом положении протечки пара через уплотнение на 10 % меньше, чем при симметричном положении гребней.
Осевой сдвиг вала турбины относительно этого положения на величину ±1 мм приводит к возрастанию расхода протечек пара через уплотнение на величину порядка 15–23 %.
Выводы
1. Проведена верификация вычислений протечек пара через диафрагменное лабиринтное уплотнение паровой турбины.
2. Выявлена большая чувствительность результатов моделирования к густоте расчетной сетки в вихревых камерах и особенно в районе радиального зазора под гребнями уплотнения.
3. Установлена зависимость протечки пара через диафрагменное уплотнение при осевом сдвиге ротора паровой турбины.
4. Предлагаемая методика и полученные результаты могут быть использованы для расчета протечек пара через лабиринтные диафрагменные уплотнения ступеней паровой турбины и при расчете осевого усилия, действующего на ступень турбины на переменных режимах ее работы.
Библиографическая ссылка
Жинов А.А., Шевелев Д.В., Гридчин Н.В. ИССЛЕДОВАНИЕ ВЛИЯНИЯ ОСЕВОГО СМЕЩЕНИЯ РОТОРА ПАРОВОЙ ТУРБИНЫ НА ВЕЛИЧИНУ ПРОТЕЧКИ ПАРА ЧЕРЕЗ ДИАФРАГМЕННОЕ УПЛОТНЕНИЕ СТУПЕНИ // Современные наукоемкие технологии. – 2020. – № 10. – С. 32-37;URL: https://top-technologies.ru/ru/article/view?id=38251 (дата обращения: 21.11.2024).