В данной работе объектом исследования является задача составления оптимального расписания регулирования электрической мощности, коммутируемой группе потребителей с применением широтно-импульсного метода (ШИМ) [1; 2]. Здесь так же, как это часто происходит при решении различных других оптимизационных задач, приходится принимать компромиссные решения – необходимо делать выбор между высокой скоростью вычислений и их точностью по отношению к оптимальности [3]. Поэтому актуальной является задача разработки алгоритма, обладающего обоими качествами – как высокой скоростью сходимости, так и получением решений, близких к оптимальным. Для решения указанной задачи в [4] рассмотрены модификации алгоритма оптимизации последовательности отбора (АОПО), позволяющие получать близкие к оптимальным расписания, так как этот алгоритм для конкретно рассматриваемой задачи показывает наивысшие результаты в отношении качества оптимизации по сравнению с рядом метаэвристических алгоритмов, включая эволюционные алгоритмы и др. [4, с. 214]. Однако время получения результатов с помощью данного алгоритма при нескольких десятках потребителей составляет около 20 минут.
Цель исследования: усовершенствование АОПО, направленное на повышение скорости сходимости к решениям, близким к оптимальным.
Материалы и методы исследования
В рассматриваемой оптимизационной задаче минимизируется целевая функция, обозначаемая C, которая рассмотрена в [5]. Значение C зависит от параметров объектов, представляющих n потребителей, и от составленного расписания. Имеются две группы параметров: T = {ti}, i = 1,...,n, которые представляют величины силы тока, и P = {pi}, i = 1,...,n, которые представляют временные продолжительности коммутации, выражаемые целыми числами в диапазоне от 0 до m, где m – число дискретных интервалов времени в расписании.
Для исследования использованы файлы исходных данных f1 – f5, представленные в [5], и некоторые другие файлы исходных данных, обладающие характерными особенностями. Во всех этих файлах описывается по n = 40 объектов, за исключением файла in28, для которого n = 28. Файл f7 имеет равномерное распределение обоих параметров по одинаковым областям значений. Еще в одном файле все значения ti = 30, i = 1,...,n.
В вышеуказанной работе также предложены алгоритмы с номерами от 1 до 34 (с некоторыми пропусками), предназначенные для минимизации C. Впоследствии номенклатура алгоритмов была расширена до 39. Некоторые из этих алгоритмов основаны на сортировке объектов по критериям с соответствующими номерами. Предложена также первоначальная версия АОПО, которая затем модифицировалась в [4].
АОПО основан на методе имитации отжига [6] и является одним из алгоритмов стохастической оптимизации [3], свойством которых является нестрогая детерминированность времени работы. Одним из важных факторов для существенного приближения к глобальному минимуму при использовании метода имитации отжига является выбор удачного начального приближения [7, с. 12]. Соответственно, в данном случае на скорость сходимости АОПО среди прочих факторов положительно влияет удачный выбор начальной последовательности (НП). НП – это получаемая каким-либо образом за небольшое время последовательность объектов, согласно которой эти объекты размещаются в расписании. АОПО использует в качестве отправной точки данную последовательность и в своей работе оптимизирует её.
НП ранее создавалась с использованием минимального из результатов минимизации с помощью алгоритмов с номерами из диапазона с 1 по 39, из которых отобраны 19 наиболее эффективных. При выборе какого-либо из указанных результатов производится их сравнение. Например, при использовании в качестве исходных данных файла f1 алгоритм 33 приводит к расписанию со значением целевой функции C33 = 2879435, а алгоритм 24 – соответственно с C24 = 2877487, т.е. алгоритм 33 приводит к решениям, на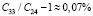 
худшим, чем при использовании алгоритма 24.
Сравнение возможно и с другой точки зрения. Для этого в [4] для данной целевой функции рассмотрено понятие теоретического минимума для входных данных, который обозначим TM. Значение глобального минимума при большой размерности входных данных определить обычно невозможно, тогда как TM можно оценить. Если сопоставлять достигаемые значения C со значением TM, то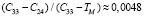 
, т.е. алгоритм 24 приводит к значениям на 0,48 % ближе к TM, чем алгоритм 33.
Проведены вычисления, показавшие, что если при НП значение C намного больше, чем значение C для расписания, получаемого алгоритмом 2, обозначаемого здесь C2, то либо образуется значительная задержка для дальнейшей оптимизации, либо при одинаковом времени выполнения достигаются худшие результаты. Так, если использовать для создания НП алгоритм 10, то C10 = 2894266, и далее при работе АОПО в течение минуты при частоте процессора 1,5 ГГц достигается значение C в среднем на 0,006 % большее, чем C2 = 2877679.
Отсюда следует предположение, что если при НП значение C, найденное алгоритмом, отличным от АОПО, будет намного меньше C2 и других значений, получаемых указанными 19 алгоритмами, то, напротив, время вычислений сократится.
Алгоритм нахождения НП
С целью выявления факторов, которые могли бы оказывать влияние на минимизацию значений C, соответствующих НП, рассмотрены ранее разработанные алгоритмы. Применение второй группы алгоритмов (с 23 по 29) в [5, с. 54] часто приводило к наилучшим результатам. Эта группа была основана на выборе объекта каждый раз того, со значением ti которого получится максимальная сумма произведений со значениями параметра T для объектов, оставшихся на данный момент невыбранными. По некоторой аналогии разработан изложенный далее алгоритм нахождения НП (алгоритм ННП).
Алгоритм, так же как и алгоритмы 23–29, основан на выборе объектов и последующем их поочередном расположении в расписании в наилучшее время без последующего перемещения. Особенность алгоритма в том, что критерием выбора является составление предварительного расписания с наименьшим значением C. То есть, когда требуется принять решение, какой объект переместить вперёд в последовательности, учитывается то, какое расписание может быть при этом получено. Аналогия состоит в том, что, так же как и ранее, учитывается результат последующих действий с невыбранными на данный момент объектами.
Алгоритм ННП использует следующие массивы:
– T, P, хранящие значения параметров соответственно ti и pi объектов, i = 1,...,n;
– M(t), хранящий средние значения ti по всем объектам, кроме текущего: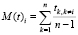 
;
– U, содержащий номера объектов;
– D размерности n×m, элементы которого указывают, имеется ли в расписании тот или иной объект в некоторый момент времени;
– W, хранящий основную информацию расписания в виде номеров моментов времени начала импульсов;
– L, Y, хранящие расписания в виде копий массивов T, P, U, W.
В алгоритме используется функция Z, имеющая на входе два параметра. Она возвращает увеличенное на заданное вторым параметром, обозначаемым z2, число процентов значение первого параметра. Алгоритм производит также обращение к внешней функции, вычисляющей значение C с временной сложностью O(n2m).
Алгоритм ННП следующий:
1) присвоить найденному значению целевой функции S ← 1000000000;
2) в цикле по переменной i, принимающей значения с 1 по n – 1:
2.1) присвоить S′ ← 1000000000;
2.2) в цикле по переменной j, принимающей значения с i + 1 по n:
2.2.1) в зависимости от заданного в начале пользователем номера алгоритма [5, с. 52] проверить соответствующее условие (критерий сортировки). Сравнение производится с использованием параметров i-го объекта и функции Z от параметров j-го объекта. Например, для 4-го критерия условием является истинность результата сравнения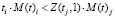 
.
2.2.2) если условие по предыдущему пункту не выполнено, то перейти к концу цикла по j (шаг 2.3);
2.2.3) обмен i-го и j-го объектов (т.е. значений элементов i и j массивов T, P, U, M(t));
2.2.4) в цикле по переменной k, принимающей значения c i + 1 по n – 1:
2.2.4.1) в цикле по переменной h, принимающей значения c k + 1 по n:
2.2.4.1.1) если h ≠ j и k ≠ j, то в зависимости от номера алгоритма [5] проверить условие (критерий сортировки), сравнивая параметры объектов k-го и h-го, без использования функции Z. Если это условие выполняется, то выполнить обмен объектов k-го с h-м;
2.2.4.2) конец цикла по h;
2.2.5) конец цикла по k;
2.2.6) комментарий: на последующих шагах (до 2.2.10) производится построение расписания;
2.2.7) обнулить все элементы массива с D1,1 по Dn,m;
2.2.8) первый объект разместить в первый момент времени следующим образом:
2.2.8.1) присвоить всем элементам массива с D1,1 по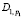 
значение 1;
2.2.8.2) присвоить W1 ← 1;
2.2.9) цикл по переменной k, принимающей значения с 2 по n. В этом цикле для k-го объекта находится наилучший начальный момент коммутации. Для этого выполнить следующее:
2.2.9.1) присвоить S" ← 1000000000; q ← 1;
2.2.9.2) цикл по переменной g, принимающей значения c 1 по m:
2.2.9.2.1) присвоить Wk ← g;
2.2.9.2.2) обнулить элементы массива c Dk,1 по Dk,m;
2.2.9.2.3) в цикле по переменной h, принимающей значения с Wk по Wk + pk – 1, если h ≤ m, то присвоить Dk,h ← 1, иначе присвоить Dk,h–m ← 1;
2.2.9.2.4) присвоить S(3) ← 0;
2.2.9.2.5) в цикле по переменной h, принимающей значения с 1 по k – 1, во вложенном цикле по переменной f с 1 по m, если Dk,f > 0 и Dh,f > 0, то увеличить S(3) на tk?th;
2.2.9.2.6) если S" > S(3), то присвоить S" ← S(3) и q ← Wk;
2.2.9.3) конец цикла по g;
2.2.9.4) помещение объекта k в наилучшую позицию следующим образом:
2.2.9.4.1) присвоить найденное значение начальному моменту: Wk ← q;
2.2.9.4.2) обнулить элементы массива c Dk,1 по Dk,m;
2.2.9.4.3) в цикле по h с q по q + pk – 1, если h ≤ m, то присвоить Dk,h ← 1, иначе Dk,h–m ← 1;
2.2.10) конец цикла по k;
2.2.11) вычислить значение C, используя внешнюю функцию;
2.2.12) если C стало меньше, чем было найдено ранее для данного i (т.е., C < S′), то запомнить это расписание (массивы T, P, U, W) в L и присвоить S′ ← C;
2.2.13) иначе обратно обменять объекты i и j;
2.3) конец цикла по j;
2.4) если было получено более оптимальное расписание, чем раньше (т.е., S′ < S), то запомнить его (т.е., присвоить Y ← L и S ← S′);
3) конец цикла по i;
4) наилучшее полученное расписание находится в Y, значение целевой функции в S. Конец.
Данный алгоритм в процессе построения множества расписаний выбирает наилучшее из них и запоминает соответствующую НП. Такое расписание не обязательно получается в конце работы данного алгоритма, оно может быть найдено на некотором этапе. Если использовать НП, получаемую в конце процесса упорядочения, она часто приводит к расписанию худшему, чем найденные ранее. Таким образом, сам процесс построения множества промежуточных расписаний играет роль метода статистических испытаний (Монте-Карло), однако при суженной области возможных значений. Применение функции Z вместо использования собственно значений параметров увеличивает количество таких испытаний, увеличивая число перестановок объектов. Это увеличивает вероятность нахождения лучшего расписания.
Результаты исследования и их обсуждение
Предлагаемый алгоритм реализован на языке Object Pascal. Анализ проведенных с файлом данных f1 вычислений показывает, что оптимальными параметрами, которые можно задать для алгоритма ННП, являются: номер критерия – 4, z2 = 20 %. Указанные параметры являются оптимальными для большинства других файлов данных с некоторыми исключениями. Так, для файла f3 оптимальное значение z2 = 10 %. Если в исходных данных все ti равны, то алгоритм работает с критерием 4 намного дольше – 70 с. Поэтому в таком случае используется критерий 2, при этом время работы 18 с с тем же результатом. Таким образом, алгоритм ННП работает различное время в зависимости от значений исходных данных. При n = 40 и z2 ∈[10 %, 20 %] это время составляет от 16 до 70 с.
При применении АОПО к получаемым НП для разных входных данных использованы оптимальные параметры [4]. Проведены серии по 7 экспериментов, каждый длительностью 1 мин, результаты усреднены, округлены и представлены в таблице, где:
– СННП – значение C, полученное с помощью алгоритма ННП;
– Сmin 19 – минимальное из значений C, полученных 19 алгоритмами;
– САОПО – значение C, полученное с помощью АОПО без применения алгоритма ННП;
– СННП + АОПО – значение C, полученное АОПО с применением алгоритма ННП;
– В – улучшение C при добавлении алгоритма ННП к АОПО в контексте приближения к TM.
Итоговые результаты вычислений для различных файлов
|
Файл |
СННП |
Сmin 19 |
САОПО |
СННП + АОПО |
TM (оценочно) |
B, % |
|
f1 |
2877282 |
2877453 |
2877265 |
2877256 |
2877210 |
16,3 |
|
f2 |
44249611 |
44249630 |
44249465 |
44248775 |
44248300 |
59,2 |
|
f3 |
116133601 |
116148720 |
116132676 |
116132437 |
116128000 |
5,1 |
|
f4 |
33981298 |
33984551 |
33977655 |
33977647 |
33972900 |
0,2 |
|
f5 |
1599457 |
1599590 |
1599448 |
1599435 |
1599413 |
37,1 |
|
f7 |
47792884 |
47796166 |
47792533 |
47792335 |
47792060 |
41,9 |
|
in28 |
1247544 |
1248327 |
1247294 |
1247082 |
1246800 |
43,0 |
Из таблицы следует, что алгоритм ННП обычно приводит к НП с меньшим значением C, чем другие алгоритмы, работающие небольшое время. Указанные 19 алгоритмов в совокупности работают около 4 с, а алгоритм ННП менее 20 с. Несмотря на значительную разницу, это во много раз меньше, чем 20 мин, поэтому алгоритм ННП безболезненно может быть использован.
Как следует из последнего столбца таблицы, во всех случаях имеется улучшение, следовательно, высказанное ранее предположение подтверждается. В среднем B составляет 29 % со среднеквадратичным отклонением 22 %. Для некоторых файлов B незначительно. Выявлена следующая связь B с особенностями таких файлов: если диапазоны изменения значений параметров узкие относительно средних значений, то B незначительно. Например, в файле f4: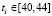 
, 
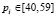, i = 1,...,n. То есть значения ti = 42 ± 2, 
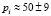. Обозначим как средние значения tср и pср числа до символа «±», и как отклонения σt и σp числа после этого символа, т.е. ti = tср ± σt, pi = pср ± σp. Отношения σt/tср и σp/pср для файлов f3 и f4 составляют от 0,05 до 0,19, а для остальных файлов, где наблюдается значительное улучшение, эти отношения принимают значения от 0,55 до 1.
Проведены также вычисления при использовании неоптимальных параметров АОПО. Они показывают, что, несмотря на то что значение C становится несколько больше, чем при использовании оптимальных параметров, добавление алгоритма ННП позволяет при дальнейшем применении АОПО за одно и то же время получать результаты ближе к TM, чем в случае без использования алгоритма ННП.
Получение за одинаковое время меньших значений C означает, что близкие к глобальному минимуму значения C достигаются при применении алгоритма ННП за значительно меньшее время, чем без его применения. Это справедливо при использовании как оптимальных параметров АОПО, так и неоптимальных, при условии равенства значений этих параметров в обоих случаях. Результаты исследований относятся к диапазону n ∈[28, 40]. Таким образом, цель работы достигнута, т.е. АОПО дополнен так, чтобы скорость его сходимости была увеличена.
Заключение
Предлагаемый алгоритм, используемый при составлении расписания коммутаций группе потребителей при ШИМ регулирования мощности, позволяет находить начальные последовательности, приводящие затем к решениям, близким к оптимальным, быстрее, чем ранее разработанными алгоритмами. Временная сложность алгоритма O(n5 + n4m2), но так как n и m одного порядка, можно считать, что временная сложность O(n4m2). Несмотря на то что это больше, чем у ранее используемых 19 алгоритмов, например у алгоритма 2 со сложностью O(n2m2), использование АОПО с предлагаемым алгоритмом за одинаковое время приводит к более оптимальным результатам.
Библиографическая ссылка
Димитриев А.П АЛГОРИТМ НАХОЖДЕНИЯ ПРИБЛИЖЕННОЙ К ОПТИМУМУ НАЧАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ОТБОРА ДЛЯ ОПТИМИЗАЦИИ РАСПИСАНИЯ // Современные наукоемкие технологии. – 2020. – № 10. – С. 27-31;URL: https://top-technologies.ru/ru/article/view?id=38250 (дата обращения: 23.11.2024).