Анализ рабочих программ, учебников по физике и математике в техническом вузе по результатам анкетирования преподавателей показал, что рабочие программы по учебным дисциплинам мало ориентированы на будущую специальность, студенты слабо мотивированы на изучение курса физики и математики. В нашем вузе начиная с 1998 г. преподавателями кафедры «Прикладная физика и математика» ежегодно проводится олимпиада по физике для студентов первого и второго курсов. В связи с новыми образовательными стандартами и компетентностным подходом в обучении специалистов возникла необходимость изменить содержание олимпиадных задач, а также изменить формат проведения.
Цель исследования: разработать методическую систему организации проведения олимпиады по физике и математике среди студентов технического вуза по специальности «Строительство» с целью формирования профессиональных компетенций, а также произвести оценку степени их формирования.
В работе исследователей С.В. Железного, И.В. Сычева, Е.А. Москалевой говорится, что формирование компетенций будущего инженера возможно при проведении предметных олимпиад [1]. В процессе организации и проведения олимпиады очень хорошо сочетаются методы контроля усвоенных знаний и установление связи между фундаментальными предметами и специальными дисциплинами, а также происходит развитие умений использовать физико-математический аппарат в новых учебных нестандартных ситуациях. Проведение предметных олимпиад побуждает к творческо-поисковой активности не только студентов, но и преподавателей.
Опираясь на основные требования ФГОС по изучаемой дисциплине, выделим следующие компетенции, которые будем формировать в ходе решения олимпиадных задач:
1) умение находить в ходе решения профессиональной задачи физические явления и закономерности, математические модели;
2) применение основных формул и понятий по физике и математике для решения задач профессиональной направленности;
3) умение применять основной математический аппарат и математические методы исследования в профессиональной сфере.
В работе [2], основываясь на исследования В.П. Беспалько, выделено пять уровней усвоения знаний студентами технического вуза при изучении дисциплины физика, которые мы будем использовать при составлении варианта олимпиадных заданий:
1 уровень знания – знания знакомства. На данном этапе подбираются задания на распознавание основных понятий, формул, физических явлений и процессов в стандартных учебных ситуациях, которые встречаются в курсе математики и физики. При решении задачи данного уровня студент узнает физический закон в условии задачи, подставляет в формулу числовые данные и производит расчет.
2 уровень знания – знания копии. На данном уровне студент самостоятельно воспроизводит информацию об объекте, применяет правильно известный алгоритм для решения задачи. При решении задачи данного уровня студент правильно применяет физические законы, но в отличие от 1 уровня студент должен грамотно синтезировать несколько формул, произвести математические преобразования, сделать числовой расчет.
3 уровень знания – эвристический. В процессе самостоятельной работы осуществляется поисковая деятельность, направленная на выявление физико-математических законов и явлений в новой профессиональной ситуации, а также предполагает продуктивное действие в решения задачи.
4 уровень знания – творческий. На основе полученных знаний, самостоятельно организует свою деятельность по решению творческой экспериментальной задачи, в ходе которой необходимо будет применить полученную информацию в новой ситуации. Студент применяет полученную информацию из условия задачи или предложенного теоретического материала для решения нового творческого задания и самостоятельно придумывает способ определения физической величины, используя предложенные экспериментальные оборудования.
5 уровень – исследовательский. При освоении заданий на этом уровне студент должен узнать проблему в задании, выдвигать свои предположения, выстроить план решения возникшей задачи, сделать выводы. В ходе освоения данного уровня студент систематизирует полученные расчеты, придумывает новые вопросы, связанные с использованием их в строительстве.
Материалы и методы исследования
Для проведения исследования проведен анализ рабочих программ по физике для направления 08.03.01 «Строительство» и других дисциплин, в которых формируются профессиональные компетенции. В отборе материала олимпиадных задач использованы учебно-методические материалы по дисциплине «Физика», «Строительная физика», «Механика грунтов», «Основы теплотехники».
Олимпиадные задачи, по нашему мнению, должны отвечать следующим требованиям:
- по структуре: работа по математике и физике состоит из пяти задач, согласно уровням усвоения знаний и различной сложности;
- по содержанию: задания должны включать в себя элементы научного творчества, желательно, чтобы формулировки задач носили привлекательный характер, формулировка задач должна описывать ситуацию, которая возникает в профессиональной деятельности будущих инженеров;
- по соответствию учебной программе: в задания рекомендуется включать задачи по разделам физики и математики, соответствующие тематическому плану прохождения студентами учебного материала. Недопустимо тематическое забегание вперёд;
- по литературе: задания должны быть подобраны из разных источников, в интернете не должно быть готового решения задач;
- по тематике: задачи должны быть представлены по всем изученным темам;
- по времени выполнения: за отведенное время студенты смогли приступить к решению всех задач;
- по уровню сложности (пять уровней). Олимпиадные задачи составлены в порядке возрастания от простого к сложному, причем предположительно с первыми двумя из них успешно справлялись примерно 60 % участников, с третьей – 50 %, с четвертой 30 %, а с последней – лишь лучшие из студентов.
Подготовка студентов к олимпиаде, а также формирование компетенций осуществляется преподавателями-предметниками на лекционных, практических и лабораторных занятиях, путем включения информации профессиональной направленности, соответствующей уровню вопросов олимпиады. С целью привлечения к участию в олимпиаде преподаватели кафедры в первой части олимпиады показывают интересные занимательные опыты по физике, по желанию студенты показывают сделанные своими руками экспериментальные установки и читают стихи на тему физика и математика.
В работе О.Ю. Павловской, В.И. Сурикова, В.И. Туровец, Н.А. Прокудина есть упоминание о четырех функциях олимпиад (стимулирующая, обучающая, контролирующая и представительская) [3]. В современном мире начинающий специалист должен уметь активно переключаться на разные виды деятельности, уметь решaть нестандартные профессиональные задачи, презентовать свою работу и выдавать свои оригинальные решения. Все эти качества современного специалиста можно развивать на предметной олимпиаде.
Авторы Ю.А. Крымская, Е.И. Титова, С.Н. Ячинова выделяют три группы математических задач при изучении темы дифференциальные уравнения: задачи, связанные с процессами выделения тепла, задачи на исследование деформации строительных сооружений и колебательных процессов, задачи на скорость протекания процессов [4].
Однако следует отметить, что в перечисленных группах математических задач в основе лежат физические явления и процессы, применяемые в строительстве, поэтому при их решении студенты должны увидеть межпредметные связи различных наук, понять, о каком физическом процессе идет речь, и подобрать нужный математический аппарат.
Олимпиадные задачи по физике для студентов 1–2 курсов.
1. Задача (знания знакомства). Для оценки относительного удлинения материала используется стальной стержень длиной 1,5 м и площадью поперечного сечения S = 1,5 мм2. Известно, что для его сжатия затрачена работа 7 Дж. Модуль Юнга примерно равен E = 220 ГПа. Высокая прочность этого материала позволяет использовать её при строительстве высотных зданий и мостов.
2. Задача (знания копии). В теории сопротивления материалов очень часто используется понятие момента инерции тела. Определить момент инерции некоторой детали, представленной на рис. 1, относительно оси вращения ОО/. Деталь состоит из двух одинаковых стержней массой m1 = m3 = 2 кг и длиной l = 40 см, шара массой m2 = 1 кг радиусом R2 и цилиндра массой m4 = 1 кг радиусом R2. Длина стержня l = 2R2.
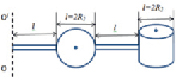
Рис. 1. Момент инерции детали
3. Задача (эвристические знания). Выберите любой объект природы, который возможно применить в строительстве, и приведите к нему как можно больше физических законов. Дайте краткие пояснения каждому случаю. Как можно применять эти законы в строительстве?
А. Возможно ли применить законы механики? Б. Какие законы молекулярной физики можно применить к данному объекту? В. Можно ли с помощью физических законов определить возраст кирпича? Г. Возможно ли применить законы квантовой механики к данному объекту? Если да, то перечислите условия.
4. Задача (творческие знания). Имеются две сплошные детали, изготовленные из стали одинаковой массы: одна изготовлена в форме шара, а другая в форме цилиндра. Эти детали катятся без трения с одинаковой скоростью по горизонтальной поверхности. 1) Определить, кинетическая энергия какой детали больше? Во сколько раз больше? 2) Какое из тел поднимется выше? Влияет ли момент инерции тела, которая часто используется в строительных расчетах, на подъем детали? 3) Придумать на основе условия задачи способ расчета момента, инерции тел, используя шар, наклонную плоскость.
5. Задача (исследовательские знания). На рис. 2 имеется кабина лифта с массой 800 кг, который может нести нагрузку до 600 кг. В подъемном устройстве лифта используется электродвигатель, который поднимет лифт с полной нагрузкой с первого этажа на третий этаж (9 м) за 30 с. Проведите исследование по предложенной схеме:
1) рассчитайте полную энергию и мощность лифта с нагрузкой; 2) для повышения эффективности данной системы можно включить противовес массой 2000 кг. Определить общую массу пассажиров, которая необходима, чтобы сбалансировать систему; 3) рассчитайте среднюю скорость лифта и кинетическую энергию; 4) на ускорение лифта требуется 10 с и столько же времени, что и на замедление. Рассчитайте наибольшую скорость лифта; 5) рассчитайте вес человека, когда лифт ускоряется при движении вверх, движется вверх на постоянной скорости; 6) сделайте вывод и придумайте на основе данного условия, как можно модернизировать данную установку [5].
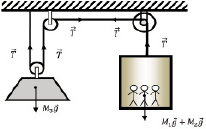
Рис. 2. Подъемное устройство лифта
Олимпиадные задачи по математике для студентов 1–2 курсов
В работе И.М. Шапиро рассмотрены задачи по математике с техническим содержанием, которые мы использовали при составлении олимпиадных задач [6].
1. Задача (знания знакомства). Для решения этого задания даётся краткая информация о методе наименьших квадратов (МНК). В результате проведения эксперимента получили данные, представленные в таблице. Используя полученные данные при гипотезе линейного снижения ρ в зависимости от нормализованного фактора xi , нужно найти две оценки через метод наименьших квадратов в модели ρ = b0 +b1 x.
Результаты эксперимента
|
xi |
-1 |
-0,5 |
0 |
0,5 |
1 |
|
ρ |
1228 |
1136 |
1120 |
1044 |
942 |
2. Задача (знания копии). Рассчитать расход бетонного раствора для заливки 10 канализационных колец с внутренним диаметром 1000 мм, внешним диаметром 1160 мм и высотой 900 мм. Сколько необходимо грузовых машин грузоподъемностью 5 т для перевозки этих колец, если плотность бетона 2200 кг/м3?
3. Задача (эвристические знания). Найти работу, совершённую железобетонной надолбой, имеющей форму правильного тетраэдра с ребром 1 м, если её извлекают с помощью подъемного крана со дна реки глубиной 5 м (плотность железобетона 2500 кг/м3, плотность воды 1000 кг/м3).
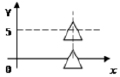
Рис. 3. Подъем железобетонной надолбы
4. Задача (творческие знания). Необходимо написать примеры использования математического аппарата при изучении специальных дисциплин, которые прошли или находятся в процессе изучения (задание известно за несколько дней до проведения олимпиады и выполняется заранее).
5. Задача (исследовательские знания). Задано уравнение, описывающее свободные колебательные процессы в строительных конструкциях x’’+2hx’ + ω2x = 0(0 < h ? ω). Найти общее решение в виде x = x(t) и исследовать поведение интегральной кривой при t → ∞.
Организация олимпиады и критерий оценивания
Задания физико-математической олимпиады студентов по специальности «Строительство» состоят из пяти задач по физике и пяти задач по математике. Студенты пишут работу 3 часа. После проверки работ проводится награждение победителей и включение баллов олимпиады в рейтинг студента по изучаемой дисциплине.
Степень формирования компетенций при проверке олимпиадной студенческой работы будем оценивать в баллах:
1. Задача (знания знакомства). Низкая степень (0–5 баллов). Если верно применяет основные понятия, формулы, то ставим 5 баллов. Средняя степень (6–8 баллов). Если задача решена, верно, но допущена математическая ошибка в расчете. Высокая степень (9–10 баллов). Если задача решена полностью. Допускаются небольшие недочёты.
2. Задача (знания копии). Низкая степень (0–11 баллов). Присваиваем 11 баллов работе студента, если он правильно применяет основные понятия, формулы. Данная задача в отличие от задачи 1, проверяет умение синтезировать несколько физических формул. Средняя степень (12–16 баллов). Верно применяются формулы, правильно проведены математические преобразования. Есть ошибка в математических расчетах. Высокая степень (18–20 баллов). Если задача решена полностью. Допускаются небольшие недочёты.
3. Задача (эвристическая). Низкая степень (0–11 баллов). Перечислены несколько физических законов, при этом студент не может объяснить их применение в строительстве. Средняя степень (12–16 баллов). Перечислены все физические законы из условия задачи, при этом студент не может объяснить их применение в строительстве. Высокая степень (18–20 баллов). Перечислены все физические законы из условия задачи, при этом дано объяснение применения этих законов в строительстве.
4. Задача (творческая). Низкая степень (0–11 баллов). Правильно ответил на первый вопрос задачи, полностью расписал применяемые законы, получил верный расчет. Средняя степень (12–16 баллов). Правильно ответил на первый и второй вопросы задачи, полностью расписал применяемые законы, получил верный расчет. Высокая степень (18–20 баллов). Студент применяет полученную информацию из 1 и 2 задания и самостоятельно придумывает способ определения момента инерции, используя предложенные экспериментальные оборудования.
5. Задача (исследовательская). Низкая степень (0–23 баллов). Правильно выполнены задания а и б, при этом расписаны физические законы. Средняя степень (24–26 баллов) Правильно выполнены задания от а до д, при этом пошагово прописаны основные физические законы, выполнены расчеты, есть необходимый график. Высокая степень (27–30 баллов). Выполнены все задания верно с полным расчетом и обоснованием использованных физических законов. В ходе решения этой задачи студент систематизирует полученные расчеты, придумывает новые вопросы, связанные со строительством.
По всем пяти задачам определяем степень сформированности компетенций по физике: низкая степень – 0–61 баллов, средняя степень – 62–82 баллов, высокая 83–100 баллов.
Результаты исследования и их обсуждение
В студенческой олимпиаде участвовали 98 студентов дневной формы обучения 1 и 2 курса ВПИ (филиал) ВолгГТУ. Олимпиада по физике проводится два раза в год (в декабре и в апреле). По результатам декабрьской олимпиады выявлено 30 % студентов с низкой степенью сформированности компетенций, средней степенью сформированности 60 % высокая степень сформированности у 10 %). По результатам апрельской олимпиады выявлено с низкой степенью сформированности компетенций 20 % студентов, средней степенью сформированности 50 %, высокая степень сформированности у 30 %.
Заключение
Обобщая и анализируя опыт своей работы, мы видим, что олимпиадная деятельность студентов способствует формированию профессиональных компетенций будущего инженера. Необходимо продолжать совершенствование преподавания математики и физики для студентов, обучающихся по направлению подготовки 08.03.01 «Строительство» на разных формах обучения, используя традиционные и новые методики.
При выполнении лабораторной работы по физике, преподаватель, организуя деятельность студентов, указывает на необходимость изучения физических законов и применения их на практике при строительных расчетах. Работая в группе, студенты детально разбирают алгоритм выполнения работы, моделируют их последствия, по возможности модернизируют. Все это, по нашему мнению, повышает уровень получаемых компетенций.
При организации самостоятельной работы студентов и для лучшего освоения компетенций необходимо включать написание рефератов и научных статей, связанных с будущей специализацией. При такой деятельности необходимо выстроить логически материал, определять актуальность исследования, определить этапы исследования, сформулировать выводы, уметь презентовать свою работу.
Авторы работ Е.Н. Хаматнурова, С.В. Дмитриева: при формировании профессиональных компетенций необходимо внедрять практико-ориентированные занятия, на которых максимально приблизить содержание и процесс учебной деятельности студентов к их будущей профессии [7]. На практических занятиях в форме дискуссий заинтересовать студентов проблематикой вопросов в области прикладной физики и математики. Активнее использовать, с учетом индивидуальных способностей, задания с эвристическим содержанием, которые направлены на творчество студента и требуют творческого самовыражения в различных предметных областях.
Библиографическая ссылка
Рахманкулова Г.А., Мустафина Д.А., Суркаев А.Л., Светличная В.Б., Матвеева Т.А., Ребро И.В., Сухова Т.А. ВНУТРИВУЗОВСКИЕ СТУДЕНЧЕСКИЕ ФИЗИКО-МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ КАК СРЕДСТВО ФОРМИРОВАНИЯ КОМПЕТЕНЦИЙ У СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА // Современные наукоемкие технологии. 2020. № 9. С. 209-214;URL: https://top-technologies.ru/ru/article/view?id=38243 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.38243



