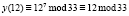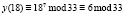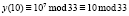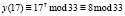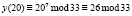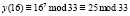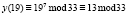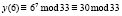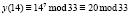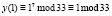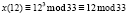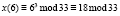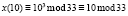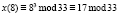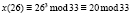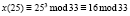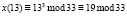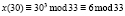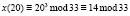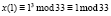Переписки с древности являлись объектом пристального внимания и несли в себе ценную информацию. Поэтому появилась необходимость в защите информации от недоброжелателей и врагов, что было наиболее востребовано в военном деле. Тогда люди начали применять различные методы для предотвращения разглашения информации. Наиболее востребованным считался метод тайнописи, когда сообщение строилось так, чтобы основная мысль была не понятна посторонним, а ясна только тем, кто был посвящен в тайну. Необходимость в защите информации востребована и в настоящее время. Именно поэтому возникла такая наука, как криптология, которая включает в себя такие направления, как криптоанализ и криптография. Криптография занимается нахождением и исследованием математических методов преобразования информации. Криптоанализ, в свою очередь, занимается поиском расшифровывания информации без знания ключей.
Криптографию можно разделить на несколько крупных разделов, первые два – это криптосистемы с открытым ключом и системы электронной подписи. Рассмотрим асимметричную криптосистему (криптосистему RSA), являющуюся фундаментальным алгоритмом шифрования с публичным ключом, она также считается самым популярным языком шифрования современности.
Целью исследования является исследование языка шифрования RSA, используемого для кодирования и декодирования информации, а также при создании электронной подписи.
Криптосистема RSA была впервые представлена в 1978 г. Р. Райвестом, А. Шамиром и А. Адлеманом. Название криптосистема RSA получила по первым буквам фамилий ее основателей. Данный язык шифрования с публичным ключом решает одну очень важную проблему: позволяет большие и длинные числа разложить на множители. Язык шифрования RSA является стандартом с 1993 г.
Рассмотрим основные понятия криптосистемы RSA. Первым шагом создания алгоритма RSA является: выбор двух простых больших натуральных чисел p и q. Затем найдем произведение этих чисел m = p?q и обозначим его как модуль шифрования. Следующим шагом найдем функцию Эйлера: 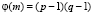 [1].
[1].
Следующий этап алгоритма: выбор показателя степени числа e, которое называют открытым показателем. Число e должно быть таким, чтобы выполнялись следующие условия: 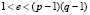 , НОД
, НОД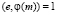 . Далее найдем d (закрытый показатель), что
. Далее найдем d (закрытый показатель), что 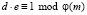 . Таким образом, получаем (m, e) – открытый ключ, (m, d) – закрытый ключ. В чем же заключается безопасность криптосистемы RSA? В том, что она основывается на неразрешимой задаче, а именно разложение модуля шифрования на множители, так как продуктивный способ поиска на данный момент времени неизвестен.
. Таким образом, получаем (m, e) – открытый ключ, (m, d) – закрытый ключ. В чем же заключается безопасность криптосистемы RSA? В том, что она основывается на неразрешимой задаче, а именно разложение модуля шифрования на множители, так как продуктивный способ поиска на данный момент времени неизвестен.
Рассмотрим преимущества использования криптосистемы RSA. Преимуществами системы RSA являются [2]: возможность открытого распространения ключей в сети Интернет; в системе RSA установлена линейная зависимость между числом занятых ключей и количеством подписчиков; самостоятельная замена чисел p и q пользователем и последующее разглашение публичного ключа общественности.
В свою очередь, у языка шифрования RSA есть свои недостатки, а именно [3]: во-первых, не существует в математике доказательства необратимости функций, используемых именно в алгоритмах асимметричного вида; во-вторых, потребность в защите от подмены публичных ключей; в-третьих, медленная скорость работы.
Сделаем вывод, что преимущества языка шифрования RSA в полной мере преобладают над его недостатками, что делает использование этой криптосистемы незаменимой, особенно в каналах связи, требующих защиты.
У криптографии с открытым ключом есть еще такой незаменимый ресурс, как генерация цифровой подписи. В чем заключается суть этого ресурса? В том, что для исходного сообщения криптосистема RSA должна будет сгенерировать дополнительный номер, и только обладатель приватного ключа сможет выполнить генерацию, и любой обладатель публичного номера сможет проверить, был ли этот номер правильно сгенерирован [4].
Только владелец пары (m, d) имеет возможность зашифровать сообщение, так как число d знает только он [5]. Допустим, злоумышленник узнал сообщение и цифровую подпись, но у него не получится возвести сообщение в известную только владельцу степень, и он не получит подпись. Для нахождения d ему необходимо вычислить 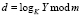 .
.
Задача на вычисление дискретного логарифма ничем не отличается от задачи факторизации, в наше время ее можно решить только при помощи квантовых компьютеров. Даже если задача факторизации выполнялась на практике, а дискретный алгоритм не был реализован. Можно сделать вывод, что данная схема передачи является надежной.
Безусловно, язык шифрования RSA с публичным ключом создает безопасный канал обмена. Пусть два собеседника общаются по открытому каналу связи. Предположим, что один из них хочет отправить другому сообщение, и для этого спрашивает публичный ключ. В процессе этого вмешивается злоумышленник и меняет публичный ключ на свой. Потом первый собеседник зашифровывает свое сообщение публичным ключом, присланным злоумышленником [6]. Однако выполнение подобной атаки является сложным, поскольку необходимо подменить сообщение от обладателя ключа, проще перехватить от первого собеседника. Именно такие атаки и являются основной угрозой криптосистем на публичных ключах. Существуют различные способы борьбы с перехватом сообщений: определяют промежуточный центр сертификации, который будет подписывать ключи вызывающего собеседника своей электронной цифровой подписью, и все возможные участники имеют доступ к открытому ключу этого центра. Например, государство может действовать как центр. На таком уровне каждый имеет право получить открытый или закрытый ключ. Открытый ключ владельца подписывается открытым ключом государства, и у владельца также есть этот открытый ключ государства. Общаясь с кем-то, они могут проверить, что открытый ключ контакта подписан государством, и они могут попробовать это, применяя открытый ключ государства.
Несмотря на надежность алгоритма цифровой подписи, у него имеются некоторые недостатки [7]: при расчете ключей необходима проверка некоторых дополнительных условий; использование очень больших целых чисел, что вызывает относительно длинные вычислительные затраты; алгоритм электронной цифровой подписи RSA дает возможность злоумышленнику, не знающему приватного ключа, сгенерировать подписи для документов, для которых результат хеширования данных может быть вычислен как произведение результатов хеширования из уже подписанных документов [8].
Для того чтобы более подробно изучить взаимосвязь между публичным и приватным ключами в языке шифрования RSA, рассмотрим пример: p = 5 и q = 11, m = p?q = 5?11 = 55; φ(m) = = 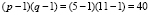 .
.
Для того чтобы вычислить все вероятные публичные ключи, нам понадобится найти числа, которые будут соответствовать двум требованиям: 1 < e < 40, НОД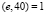 .
.
С помощью алгоритма Евклида вычислим НОД 39 раз. Все возможные публичные ключи представлены в табл. 1.
Таблица 1
Набор публичных ключей
|
Открытый ключ |
1 |
3 |
7 |
9 |
11 |
13 |
17 |
19 |
|
21 |
23 |
27 |
29 |
31 |
33 |
37 |
39 |
Чтобы найти приватный ключ, можно применить также алгоритм Евклида, но только получится 16 раз (в соответствии с количеством публичных ключей).
В качестве примера возьмем число 33 – публичный ключ. В результате получим разложение НОД, которое представлено в табл. 2.
Таблица 2
Линейное разложение НОД
|
q |
u1 |
v1 |
u2 |
v2 |
u3 |
v3 |
|
- |
0 |
1 |
1 |
0 |
40 |
33 |
|
1 |
1 |
-1 |
0 |
1 |
33 |
7 |
|
4 |
-1 |
5 |
1 |
-4 |
7 |
5 |
|
1 |
5 |
-6 |
-4 |
5 |
5 |
2 |
|
2 |
-6 |
17 |
5 |
-14 |
2 |
1 |
Таким образом, получили приватный ключ – 17. После приведенных вычислений получаем публичные и определенные им приватные ключи (табл. 3).
Таблица 3
Пары соответственных публичных и приватных ключей
|
Публичный ключ |
1 |
3 |
7 |
9 |
11 |
13 |
17 |
19 |
|
Приватный ключ |
1 |
-13 |
-17 |
9 |
11 |
-3 |
-7 |
19 |
|
Публичный ключ |
21 |
23 |
27 |
29 |
31 |
33 |
37 |
39 |
|
Приватный ключ |
-19 |
7 |
3 |
-11 |
-9 |
17 |
13 |
-1 |
Можно отметить, что графики соотношений публичного и приватного ключей в языке шифрования RSA являются симметричными относительно осей ОХ и OY.
Данную симметричность точек удобно использовать для поиска приватных ключей, которые будут соответствовать публичным ключам [8].
При расчете нужно сначала вычислить все значения приватного ключа, симметричные ему, что позволит произвести расчет намного быстрее. Допустим, точка с такими координатами, как (открытый ключ, закрытый ключ), будет соответствовать оси симметрии, значит, этой точке будет принадлежать иная точка с такими же симметричными координатами, если же это не соблюдается, то она будет совпадать ещё с тремя точками.
Попробуем разобраться в этом алгоритме с помощью примера, где p = 5 и q = 11.
Используем известный нам набор открытых ключей (табл. 1), чтобы найти закрытые ключи, также будем использовать алгоритм Евклида:
1. Возьмем открытый ключ e = 1, закрытый ключ d = 1. Получается точка с координатами (1, 1), которая соответствует оси симметрии y = x → возможно обнаружить ещё точку (39, 39).
2. e = 3, d = 27. Точка (3, 27) не соответствует осям симметрии → возможно обнаружить ещё точки: (13, 37), (27, 3), (37, 13).
3. e = 7, d = 23. Точка (7, 23) не соответствует осям симметрии → возможно обнаружить ещё точки: (17, 33), (23, 7), (33, 17).
4. e = 9, d = 9. Точка (9, 9) соответствует оси симметрии y = x → возможно обнаружить ещё точку: (31, 31).
5. e = 11, d = 11. Точка (11, 11) соответствует оси симметрии y = x → возможно обнаружить ещё точку: (29, 29).
6. e = 19, d = 19. Точка (19, 19) соответствует оси симметрии y = x → возможно обнаружить ещё точку: (21, 21).
Обратим внимание, что когда вычисляли закрытый ключ с помощью алгоритма Евклида, нам потребовалось выполнить алгоритм шестнадцать раз, а используя ось симметрии – шесть раз. Таким образом, использование нового алгоритма является более рациональным.
Приведем еще один пример на нахождение открытого и закрытого ключей.
1 шаг. Выберем два различных простых числа, допустим, p = 61 и q = 53.
2 шаг. Найдем m = p?q = 61?53 = 3233.
3 шаг. Вычислим значение функции Эйлера от числа m:
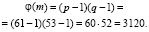
4 шаг. Выбираем такое число, чтобы соответствовал условию 1 < e < 3120. Пусть e = 17.
5 шаг. Находим d. Для этого нам понадобится формула 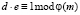 .
.
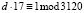 , d = 413.
, d = 413.
Пара чисел открытого ключа (3233, 17), пара закрытого ключа (3233, 413).
Для того чтобы зашифровать x = 65, нам нужно вычислить
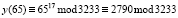 .
.
Чтобы выполнить дешифрование y = 2790, необходимо вычислить
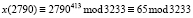 .
.
Исходное сообщение совпало с сообщением, полученным после выполнения дешифрования, из этого следует, что все шаги алгоритма выполнены правильно.
Итак, теперь мы приступим к шифрованию и дешифрованию текстового сообщения. Рассмотрим язык шифрования RSA на небольшом примере. Покажем, в чем заключается принцип шифрования и дешифрования. Исходное сообщение: «КРИПТОСИСТЕМА».
I. Определим числа p и q – простые. Для данного примера выберем p = 3 и q = 11.
II. Находим модуль шифрования m = p?q = 3?11 = 33.
III. Найдем функцию Эйлера от модуля шифрования:
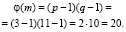
IV. Подберем число е, такое, что 1 < e < 20, НОД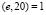 . Выберем e = 7.
. Выберем e = 7.
V. Найдем число d, исходя из условия: 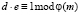 .
.
Получаем
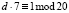 ;
; 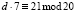 ; d = 3.
; d = 3.
VI. Публичный ключ представляет собой пару чисел (33, 7), а приватный ключ – (33, 3).
VII. Выполним шифрование нашего сообщения «КРИПТОСИСТЕМА». Представим сообщение числами из диапазона от 1 до 33 (табл. 4).
Таблица 4
Представление букв числами
|
Буква |
К |
Р |
И |
П |
Т |
О |
С |
И |
С |
Т |
Е |
М |
А |
|
Число |
12 |
18 |
10 |
17 |
20 |
16 |
19 |
10 |
19 |
20 |
6 |
14 |
1 |
Для шифрования сообщения нам необходим публичный ключ (33, 7), текст «КРИПТОСИСТЕМА» и формула, по которой происходит непосредственное вычисление: 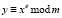 , x – это исходное сообщение, а y – зашифрованное. Все вычисления представлены в табл. 5.
, x – это исходное сообщение, а y – зашифрованное. Все вычисления представлены в табл. 5.
Таблица 5
Зашифровка сообщения «КРИПТОСИСТЕМА»
|
Исходная буква |
Вычисление |
Зашифрованная буква |
|
К |
|
К |
|
Р |
|
Е |
|
И |
|
И |
|
П |
|
Ж |
|
Т |
|
Ш |
|
О |
|
Ч |
|
С |
|
Л |
|
Е |
|
Ь |
|
М |
|
Т |
|
А |
|
А |
В итоге у нас получилось зашифрованное сообщение «КЕИЖШЧЛИЛШЬТА».
Теперь, чтобы проверить вычисления и убедиться в их правильности, дешифруем сообщение «КЕИЖШЧЛИЛШЬТА».
Чтобы расшифровать сообщение, возьмем приватный ключ (33, 3), сообщение «КЕИЖШЧЛИЛШЬТА», формулу для вычисления: 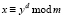 . Все вычисления представлены в табл. 6.
. Все вычисления представлены в табл. 6.
Таблица 6
Расшифровка сообщения «КЕИЖШЧЛИЛШЬТА»
|
Зашифрованная буква |
Вычисление |
Исходная буква |
|
К |
|
К |
|
Е |
|
Р |
|
И |
|
И |
|
Ж |
|
П |
|
Ш |
|
Т |
|
Ч |
|
О |
|
Л |
|
С |
|
Ь |
|
Е |
|
Т |
|
М |
|
А |
|
А |
Выполнив расшифровку сообщения «КЕИЖШЧЛИЛШЬТА», в результате получили исходное сообщение «КРИПТО- СИСТЕМА», что говорит о достоверности выполнения алгоритма RSA.
Выводы
Таким образом, можно сделать следующие выводы: криптосистема RSA является актуальной и в настоящее время. Этот метод шифрования нельзя назвать самым безопасным, так как он был разработан еще в ХХ веке. Однако для современных технологий алгоритм RSA используется и сегодня, например для передачи зашифрованных ключей. С наступлением времени электронного документооборота возникла необходимость создания электронной цифровой подписи. Она необходима, прежде всего, для признания официальности документов. Электронная цифровая подпись представляет собой перевод данных на язык криптографии. Электронная цифровая подпись и криптосистема RSA – это неделимый союз, поскольку они не могут существовать друг без друга. В Глобальной сети есть два вида ключей – это публичный и приватный. Если публичный ключ доступен любому пользователю, то приватный является защищенным от третьих лиц. Благодаря криптосистеме RSA документ является зашифрованным, но открыть доступ к нему можно в любое время. Дешифрование подписи для проверки происходит при помощи приватного ключа, а предоставление доступа к заверенному документу – через публичный ключ.
Библиографическая ссылка
Храмова Н.А. ИССЛЕДОВАНИЕ КРИПТОСИСТЕМЫ RSA ДЛЯ ШИФРОВАНИЯ ИНФОРМАЦИИ // Современные наукоемкие технологии. 2020. № 9. С. 88-93;URL: https://top-technologies.ru/ru/article/view?id=38220 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.38220