Моделирование и планирование территорий, зданий и сооружений с учетом пешеходных потоков стало очень значимым в последнее время. В качестве примера можно привести здания аэропортов, торговых центров, ночных клубов, спортивных и концертных площадок. При их проектировании должна учитываться также возможность максимально безопасной эвакуации в случае чрезвычайных происшествий.
С этой целью разрабатываются модели пешеходных потоков, изучается и моделируется поведение людей в стандартных штатных ситуациях и в случае паники. В течение последних сорока лет разработана масса моделей различной степени детализации, для различных областей применения. Микроскопические модели определяют позицию и поведение отдельных пешеходов. Среди них следует отметить модель социальных сил и модель клеточных автоматов [1; 2] как наиболее популярные. Мезоскопические модели решают проблемы определения вероятности возникновения и величины очередей, скорости отдельных пешеходов, дистанции между ними. К ним относят, например, модель Больцмана. Макроскопические модели определяют глобальные параметры потока, такие как скорость и плотность [3; 4].
Несмотря на то что пешеходный поток гораздо менее организован, чем транспортный, существует феномен самоорганизации пешеходного потока [2; 5]. То есть без участия внешнего воздействия по прошествии некоторого времени поток пешеходов, движущихся в данном направлении, приобретает достаточно устойчивые параметры.
Актуальной задачей является разработка математической модели, позволяющей определять параметры плотных пешеходных потоков для управления ими в режиме реального времени.
Целью данной работы является разработка аналитического аппарата, позволяющего на мезоскопическом уровне определять параметры плотного пешеходного потока в случае эвакуационных сценариев.
Материалы и методы исследования
Многие модели пешеходных потоков на макроскопическом и мезоскопическом уровне построены по аналогии с потоками транспортных средств. С учетом эффекта самоорганизации потока пешеходов можем рассматривать его как случайный поток событий. Под событием будем понимать достижение пешеходом точки пространства с фиксированной координатой по направлению движения потока. Интервал между событиями – это время между двумя последовательными прибытиями пешеходов к линии с данной фиксированной координатой. По данным многочисленных исследований, плотный поток пешеходов согласуется с нормальным распределением. Для получения возможности применять методы теории массового обслуживания будем считать поток пешеходов подчиненным закону Эрланга, который при значении параметра k ≥ 5 близок к нормальному закону распределения. Аналогичная гипотеза была принята и подтверждена экспериментально автором данной статьи в модели транспортных потоков TIMeR_Mod [6].
Результаты исследования и их обсуждение
Как мы уже отметили, закон Эрланга при значениях параметра k ≥ 5 близок к нормальному и соответствует плотным потокам событий. Поэтому при эвакуации из мест массового скопления людей по узким коридорам поток пешеходов будем аппроксимировать законом Эрланга (как и транспортный). Для получения параметров эффективности эвакуации пешеходных потоков будем применять методы теории массового обслуживания и теории случайных процессов [7; 8].
1. Моделирование пешеходного потока как системы массового обслуживания
Пусть время обслуживания распределено по показательному закону с параметром μ. Поток заявок распределен по обобщенному закону Эрланга с параметрами λ0, λ1,…, λк порядка (k + 1). Обслуживаться могут не более n требований одновременно. Как известно, поток Эрланга порядка (k + 1) получается из простейшего, если оставить каждое (k + 1)-е событие, а промежуточные k отбросить. Поэтому для нахождения вероятности того, что обслуживается m (n > m) требований, применим метод псевдосостояний (рисунок).

Псевдосостояния распределения Эрланга порядка k + 1
В работе автора [9] при рассмотрении транспортных потоков уже были выведены формулы для выражения вероятности пребывания системы в данном псевдосостоянии. Поэтому сейчас воспользуемся готовым результатом.
Введем следующие обозначения:
pn(t), pn+1(t), …, pn+i(t), … пребывания системы в состояниях s0, s1, …, si, … соответственно;
Un+i – состояние системы, при котором все n каналов обслуживания заняты, в очереди i требований;
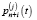 – вероятность пребывания системы в транзитивном состоянии
– вероятность пребывания системы в транзитивном состоянии 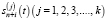 ;
;
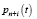 – вероятность нахождения в очереди i требований в момент t.
– вероятность нахождения в очереди i требований в момент t.
Дифференциальные уравнения для определения вероятностей нахождения системы в транзитивных состояниях Un+i имеют вид:
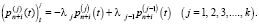 (1)
(1)
Система дифференциальных уравнений для нахождения вероятностей наличия i требований в очереди:
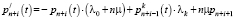
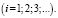 2)
2)
Дифференциальное уравнение для момента, когда нет очереди и заняты m (m ≤ n) каналов обслуживания (состояние Um):
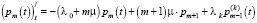
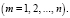 (3)
(3)
Для момента, когда система полностью свободна, дифференциальное уравнение имеет вид:
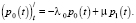 (4)
(4)
Обозначим 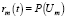 , то есть rm(t) – вероятность пребывания системы в состоянии Um . Согласно законам теории вероятностей:
, то есть rm(t) – вероятность пребывания системы в состоянии Um . Согласно законам теории вероятностей:
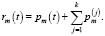 (5)
(5)
Тогда средняя ожидаемая длина очереди в момент времени t:
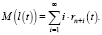 (6)
(6)
Решение данной системы дифференциальных уравнений для стацинарного процесса приведено в работе автора [9], поэтому приведем готовый результат:
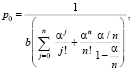 (7)
(7)
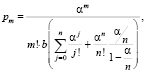
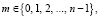 (8)
(8)
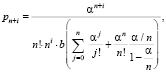
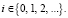 (9)
(9)
Показатели эффективности функционирования системы при условии (α/n) < 1 следующие:
1) вероятность нахождения не более s требований в очереди равна:
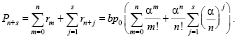 (10)
(10)
2) математическое ожидание числа требований в очереди:
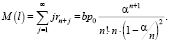 (11)
(11)
При вычислении показателей эффективности применялся метод псевдосостояний, при котором временная ось «растягивалась» в (k + 1) раз. Поэтому для «состыковки» результатов примем:
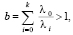
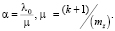 (12)
(12)
2. Определение параметров пешеходных потоков перед эвакуационным выходом
В формулах (12) mZ – среднее время обслуживания одного клиента. Рассматривая поток пешеходов как поток Пальма, в котором интервалы по времени имеют (специальный) закон распределения Эрланга с параметрами k = 6 и λ, получим следующие значения параметров:
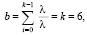
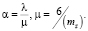 (13)
(13)
Для определения среднего количества пешеходов в очереди перед эвакуационным выходом и вероятности нахождения в очереди не более s пешеходов следует подставить в формулы (10) и (11) значения, определяемые по формуле (13).
Суммарный поток, полученный при слиянии s плотных пешеходных потоков можно также аппроксимировать с помощью (специального) закона Эрланга порядка k = 6. Второй параметр распределения при этом определяется как сумма исходных:
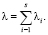 (14)
(14)
Если при этом среднее время эвакуации через каждый из n выходов равно mZ, то среднее количество людей, скопившихся у выхода, вычисляетя по той же формуле:
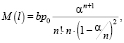 (15)
(15)
где 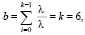
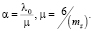
3. Определение функции распределения суммарного потока, получаемого при слиянии s плотных пешеходных потоков
В пункте 2 для определения количества пешеходов в очереди мы предположили, что суммрный поток также имеет распределение Эрланга. Если требуется определить вероятность того, что за время T0 к точке пространства с фиксированной координатой в суммарном потоке не подойдет ни один пешеход, следует более точно определить функцию распределения суммарного потока.
Для вывода функции распределения интервалов по времени в суммарном потоке воспользуемся методом, приведенным в работе [7]. Пусть τ* произвольная точка в суммарном потоке 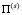 , не совпадающая ни с одним из событий в независимых потоках
, не совпадающая ни с одним из событий в независимых потоках 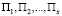 . Тогда время, оставшееся до появления очередного события в суммарном потоке, равно
. Тогда время, оставшееся до появления очередного события в суммарном потоке, равно 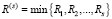 .
.
В случае справедливости гипотезы о распределении интервалов в потоке по закону Эрланга, согласно теории случайных процессов, вероятности того, что время Q, прошедшее после последнего прибытия автомобиля, и время R, оставшееся до очередного прибытия, меньше некоторого наперед заданного значения Т0, выражаются формулами:
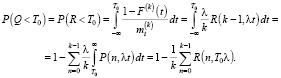 (16)
(16)
Здесь приняты обозначения:
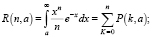
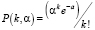 (17)
(17)
Итак, функция распределения времени, оставшегося до наступления очередного события в потоке Эрланга порядка ki, имеет вид:
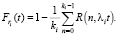 (18)
(18)
Функция распределения минимальной из s случайных величин определяется по формуле:
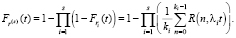 (19)
(19)
Функция распределения интервалов по времени T(s) в суммарном потоке П(s) определяется по формуле:
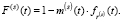 (20)
(20)
Математическое ожидание интервала между событиями в потоке Пi равно 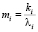 . Тогда
. Тогда
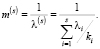 (21)
(21)
Найдем плотность распределения 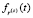
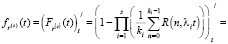
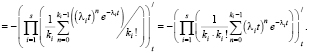 (22)
(22)
В частности, если сливаются два потока Пальма, интервалы по времени в котором распределены по (специальному) закону Эрланга порядка k = 6 с параметрами λ1 и λ2, то
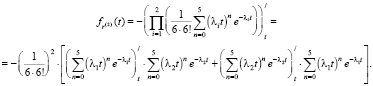 (23)
(23)
Найдем производную, подставим в формулу (23) и упростим:
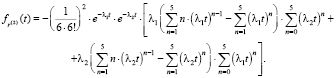 (24)
(24)
Таким образом, функция распределения интервалов по времени в потоке, полученном при слиянии двух пешеходных потоков, распределенных по закону Эрланга порядка k = 6 с параметрами λ1 и λ2, следующая:
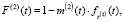 (25)
(25)
где функция 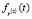 определяется по формуле (24), а математическое ожидание интервала между событиями равно:
определяется по формуле (24), а математическое ожидание интервала между событиями равно:
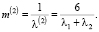 (26)
(26)
Вероятность того, что за время T0 к точке пространства с фиксированной координатой в суммарном потоке не подойдет ни один пешеход:
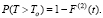 (27)
(27)
А вероятность противоположного события, то есть того, что пойдойдет хотя бы один:
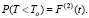 (28)
(28)
Заключение
Представленная модель пешеходного потока позволяет в режиме реального времени по минимальному количеству исходных данных определять отдельные параметры эффективности организации эвакуационного процесса. Кроме того, ее можно применять при организации улично-дорожного движения с целью определения задержек транспортных средств и пешеходов у перекрестков. Преимущество модели перед имитационными микромоделями заключается также в скорости расчетов с ее помощью благодаря аналитическому аппарату.
Библиографическая ссылка
Наумова Н.А., Карачанская Т.А. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ ЭВАКУАЦИИ ПЛОТНОГО ПЕШЕХОДНОГО ПОТОКА // Современные наукоемкие технологии. 2020. № 9. С. 42-47;URL: https://top-technologies.ru/ru/article/view?id=38212 (дата обращения: 28.02.2026).
DOI: https://doi.org/10.17513/snt.38212



