Системы автоматического регулирования являются неотъемлемой частью АСУ ТП современного производства. Традиционно для решения задачи регулирования (стабилизации) технологических переменных используются одноконтурные и многоконтурные системы, основанные на классических законах ПИ или ПИД регулирования. Такие системы успешно справляются с поставленной задачей, обеспечивают регулирование с заданной точностью. Однако повышение качества регулирования технологических переменных остается актуальной задачей. В последнее время широкое применение получили интеллектуальные системы автоматического регулирования, в частности системы на основе нечеткой (fuzzy) логики. Такие системы получили распространение в химической и нефтегазовой отраслях [1–3], энергетике [4, 5] и пр. Особое внимание уделяется системам автоматического регулирования температуры [6–8]. Как показывает практика, использование нечетких систем автоматического регулирования позволяет улучшить качество процесса регулирования технологических переменных, что благоприятно сказывается на эффективности производства.
Для большинства технологических объектов, функционирующих под управлением систем автоматического регулирования, параметры настройки ПИ или ПИД регулятора, как правило, определены либо аналитически, либо в режиме автонастройки управляющего устройства, либо иными способами. При переходе к нечеткой системе регулирования необходима методика определения параметров настройки fuzzy-регулятора. В связи с этим целью исследования является разработка такой методики, а также моделирование нечеткой системы управления с целью оценки ее работоспособности и качества регулирования.
Материалы и методы исследования
Формирование структуры нечеткого регулятора предполагает несколько этапов [9, 10]. На начальном этапе выбраны лингвистические переменные. Для ПИ-подобного нечеткого регулятора входными переменными являются X1 – сигнал (ошибка) рассогласования и Х2 – интеграл сигнала рассогласования. В структуре ПИД-подобного нечеткого регулятора дополнительно предусмотрена входная переменная X3 – производная сигнала рассогласования. В обоих случаях выходная переменная Y только одна. Для описания лингвистических переменных X1, X2 и Y выбраны следующие универсальные значения функций принадлежности [11, 12]: negative big (NB), negative medium (NM), negative small (NS), zero (ZE), positive small (PS), positive medium (PM), positive big (PВ). База правил нечеткой логики ПИ-регулятора формируется по правилу Мамдани в соответствии с таблицей.
Правила нечеткой логики ПИ-регулятора
|
X1 X2 |
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
NB |
NB |
NB |
NB |
NB |
NM |
NS |
ZE |
|
NM |
NB |
NB |
NB |
NM |
NS |
ZE |
PS |
|
NS |
NB |
NB |
NM |
NS |
ZE |
PS |
PM |
|
ZE |
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
PS |
NM |
NS |
ZE |
PS |
PM |
PB |
PB |
|
PM |
NS |
ZE |
PS |
PM |
PB |
PB |
PB |
|
PB |
ZE |
PS |
PM |
PB |
PB |
PB |
PB |
Условная часть каждого правила формируется термами первого столбца и первой строки, заключительная – термом, находящимся на пересечении соответствующего столбца и строки. Условная часть объединяется логической функцией AND, например IF (X1 = NS) AND (X2 = PS) THEN (Y = ZE) и т.д. Для функции принадлежности переменной X3 выбраны значения: negative (N), zero (ZE) и positive (P). База правил нечеткой логики ПИД регулятора по правилу Мамдани дополняется следующими правилами: IF (X3 = N) THEN (Y = N), IF (X3 = ZE) THEN (Y = ZE) и IF (X3 = P) THEN (Y = P).
Диапазон изменения лингвистических переменных определяется, исходя из параметров настройки ПИД регулятора, передаточная функция которого имеет вид
Wр(p) = P + I?p + D?p, (1)
где P = kр,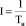 
, D = Tд, kр, Tи, Tд – параметры настройки ПИД регулятора (коэффициент регулятора, время интегрирования и время дифференцирования соответственно).
Диапазоны изменения лингвистических переменных нечеткого регулятора могут быть установлены следующим образом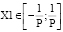 
, 
, 
, 
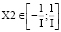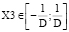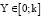, где верхняя граница k при единичном ступенчатом воздействии варьируется от 1,1 до 2, чтобы выходной сигнал регулятора мог компенсировать это возмущение. По мере увеличения значения k уменьшается динамическая ошибка, но возрастают время регулирования и число колебаний переходного процесса. Поэтому рекомендуется k выбирать равным значению, при котором устанавливается оптимальное соотношение между величиной динамической ошибки, временем регулирования и количеством колебаний.
Методика настройки нечеткого регулятора показана на примере системы автоматического регулирования температуры эмулятора печи ОВЕН ЭП10. Выбор объекта управления обусловлен в первую очередь тем, что температура является наиболее часто регулируемой технологической переменной в условиях химического, нефтегазового и других производств. Настройку системы автоматического регулирования предпочтительнее проводить на натурной модели объекта управления, которая выполняется, как правило, в виде лабораторного стенда. Эмулятор ЭП10 имеет унифицированные входные и выходные сигналы, поэтому может быть легко интегрирован в систему автоматического регулирования лабораторного стенда под управлением практически любого современного программируемого логического контроллера.
Результаты исследования и их обсуждение
В результате исследования динамики эмулятора печи ОВЕН ЭП10 получено его математическое описание [13]. Структурная и параметрическая идентификация проводилась по результатам активного эксперимента с последующей обработкой кривой разгона «методом касательной». Полученные параметры передаточной функции уточнялись с помощью программы, реализующей методы численного решения оптимизационной задачи. При аппроксимации разгонной характеристики объекта управления наилучший результат обеспечивает взвешенный критерий.
Передаточная функция объекта управления представлена в виде апериодического звена второго порядка:
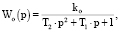(2)
где kо – коэффициент объекта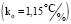 
;
T1, T2 – постоянные времени (T1 = 4,12 мин, T2 = 0,99 мин).
Передаточная функция (2) наиболее точно описывает объект управления. Зона чистого запаздывания отсутствует. Полное запаздывание определяется только емкостным запаздыванием, что характерно для реального объекта. При этом кривая разгона достаточно точно аппроксимирует начальный участок экспериментальных данных [13].
Параметры настройки ПИ и ПИД регуляторов определены программными средствами, предполагающими приближенный расчет регулятора. Полученные значения параметров настройки обеспечивают в замкнутой системе устойчивый процесс регулирования [13]:
- для ПИ регулятора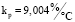 
, Tи = 0,112 мин или в соответствии с (1) P = 9,004, I = 8,929;
- для ПИД регулятора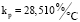 
, Tи = 0,017 мин, Tд = 3,507 мин или в соответствии с (1) P = 28,510, I = 58,824, D = 3,507.
Определены диапазоны варьирования лингвистических переменных:
- нечеткого ПИ регулятора: X1∈[–0,111; 0,111], X2∈[–0,112; 0,112], Y∈[0; 1,5];
- нечеткого ПИД регулятора: X1∈[–0,035; 0,035], X2∈[–0,017; 0,017], X3∈[–0,285; 0,285], Y∈[0; 1,6].
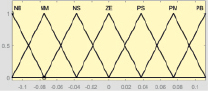
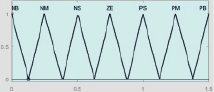
Формирование структуры нечеткой системы автоматического регулирования выполнено в среде MatLAB. Фаззификация и дефаззификация сигналов осуществляются с помощью набора треугольных термов, соответствующих значениям функций принадлежности лингвистических переменных ПИ и ПИД регуляторов (рис. 1 и 2). Термы выходной переменной Y выбраны непересекающимися с целью повышения четкости регулирования.
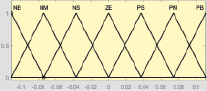
X1 X2
Y
Рис. 1. Термы входных (Х1, Х2) и выходной (Y) переменных ПИ регулятора
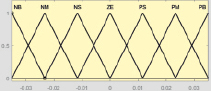
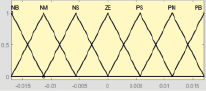
X1 X2
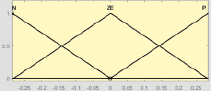
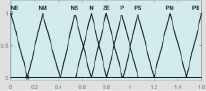
X3 Y
Рис. 2. Термы входных (Х1, Х2, Х3) и выходной (Y) переменных ПИД регулятора
Моделирование классической и нечеткой систем автоматического регулирования температуры эмулятора печи ОВЕН ЭП10 выполнено в приложении Simulink (рис. 3). Результаты моделирования в виде кривых переходного процесса, демонстрирующих реакцию систем на входное единичное ступенчатое воздействие, представлены на рис. 4. Визуальный анализ графиков переходных процессов позволяет говорить об устойчивости систем автоматического регулирования. В качестве основных прямых показателей качества регулирования выбраны динамическая ошибка (yд, °С) и степень затухания (ψ).
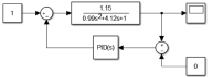
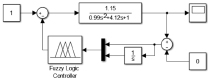
а б
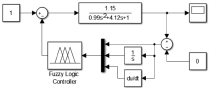
в
Рис. 3. Модели систем автоматического регулирования: а – классическая; б – нечеткая с ПИ регулятором; в – нечеткая с ПИД регулятором
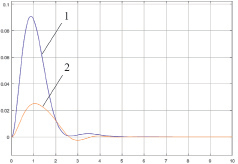
а
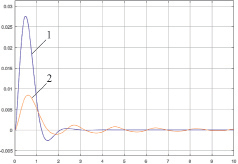
б
Рис. 4. Результаты моделирования систем автоматического регулирования: а – ПИ регулятор; б – ПИД регулятор; 1 – классическая система автоматического регулирования; 2 – нечеткая система автоматического регулирования
По кривым переходного процесса получены следующие значения показателей качества регулирования:
- для классической системы с ПИ регулятором: yд = 0,09 °С, ψ = 1, с ПИД регулятором: yд = 0,028 °С, ψ = 0,988;
- для нечеткой системы с ПИ регулятором: yд = 0,025 °С, ψ = 0,976, с ПИД регулятором: yд = 0,0085 °С, ψ = 0,859.
Анализ показателей качества регулирования говорит о том, что системы автоматического регулирования обладают достаточным запасом устойчивости (ψ > 0,75). Использование нечеткого регулятора в системе автоматического регулирования температуры позволяет снизить динамическую ошибку более чем в 3 раза, что подтверждает его эффективность.
Заключение
Предложена методика формирования структуры нечеткой системы автоматичес- кого регулирования технологических переменных на примере регулирования температуры эмулятора печи ОВЕН ЭП10. Мето- дика включает следующие этапы: выбор лингвистических переменных нечеткого регулятора; определение диапазонов их варьирования на основе известных значений параметров настройки классических ПИ и ПИД регуляторов; определение значений функций принадлежности; формирование базы правил; выбор логического способа формирования каждого правила; выбор формы термов, необходимых для фаззификации и дефаззификации сигналов в системе регулирования.
Структура нечеткой системы автоматического регулирования температуры эмулятора печи ОВЕН ЭП10 разработана в системе MatLAB. Моделирование классической и нечеткой систем автоматического регулирования температуры выполнено в приложении Simulink.
Нечеткие системы автоматического регулирования на основе ПИ и ПИД регуляторов являются работоспособными. Такие системы обладают достаточным запасом устойчивости и справляются с регулированием температуры эффективнее, чем классические системы автоматического регулирования, что подтверждается улучшением прямых показателей качества регулирования.
Использование нечетких систем автоматического регулирования в составе АСУ ТП вместе с системами, реализующими классические законы регулирования, или взамен последних позволяет повысить эффективность и надежность выполнения функций автоматического управления.
Предложенная методика формирования структуры нечеткой системы автоматического регулирования апробирована на примере системы автоматического управления эмулятором печи ОВЕН ЭП10 и может быть рекомендована при автоматизации объектов энергетики, химической, нефтегазовой и других отраслей промышленности.
Библиографическая ссылка
Котляров Р.В., Пачкин С.Г. МОДЕЛИРОВАНИЕ НЕЧЕТКОЙ СИСТЕМЫ УПРАВЛЕНИЯ ЭМУЛЯТОРОМ ПЕЧИ ОВЕН // Современные наукоемкие технологии. – 2020. – № 9. – С. 26-31;URL: https://top-technologies.ru/ru/article/view?id=38209 (дата обращения: 19.04.2024).