Электромагниты постоянного тока находят применение во множестве областей жизни человека. Они используются для управления потоками среды (газовой, жидкой), в качестве замков, в устройствах механического сопряжения (муфтах). В связи с этим они встречаются в водоснабжении, агрокультуре, системах компрессии воздуха (как разгрузочные клапаны), центральном отоплении, автомобильных мойках и заправках, непосредственно в автомобиле, в бытовой технике. На работу электромагнита оказывают влияние характеристики, форма и состав его составных частей. Однако экспериментально определить влияние отклонения характеристик отдельных частей электромагнита на его рабочую характеристику трудо- и времязатратно. Чтобы нивелировать этот недостаток, предлагается осуществить моделирование электромагнита. При помощи модели можно рассмотреть работу электромагнита при различных отклонениях магнитных свойств деталей и определить степень влияния каждой из них в различных сочетаниях.
Рабочий процесс электромагнита основан на преобразовании электрической энергии в механическую и, как результат, в прямолинейное движение. Связывают это преобразование электромагнитные силы, распространяющиеся по структуре электромагнита [1], представленной на рис. 1.
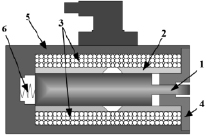
Рис. 1. Техническое устройство электромагнита
В работе электромагнита участвуют: корпус (5), якорь (1), осуществляющий перемещение под действием электромагнитного поля, создаваемого рабочей обмоткой (3), фланца (4) для закрепления элементов внутри корпуса. Для возврата якоря в исходное положение используется пружина (6). Чтобы линеаризовать зависимость перемещения якоря от тока, протекающего через обмотку, между якорем и обмоткой устанавливается магнитный шунт (2), выполненный из магнитомягкого материала с немагнитной вставкой.
Поскольку электромагнит представляет собой структуру из деталей с магнитной проводимостью, то важно рассматривать влияние отклонений магнитных характеристик его составных частей на рабочую характеристику. В качестве характеристики магнитных свойств деталей используют зависимость магнитной индукции и напряженности магнитного поля – B-H кривую [2]. При перемагничивании деталей образуется семейство графиков таких зависимостей, именуемых петлями гистерезиса [3; 4].
При первоначальном увеличении напряженности магнитного поля (и условии, что материал был в размагниченном состоянии) возрастающая индукция образует кривую, которая называется кривой первоначального намагничивания. Если после того, как напряженность магнитного поля и индукция достигают максимума, начать снижать значение напряженности до нуля, то произойдет уменьшение величины магнитной индукции до некой величины, отличной от нуля. При увеличении напряженности магнитного поля обратной величины произойдет переход через точку коэрцитивной силы, где напряженность равна нулю, и возрастание индукции также с противоположным знаком вплоть до максимальных значений. Эта точка будет симметрична относительно центра координат точке положительных максимальной напряженности и индукции насыщения. Обратный переход напряженности магнитного поля от отрицательных величин к максимальной положительной завершит общий график характеристики материала – предельной петли гистерезиса. Особенность этой петли в том, что внутри ее границ будут находиться все остальные петли гистерезиса этого материала. А через вершины этих петель пройдет кривая, соединяющая начало координат и точку с индукцией насыщения, именуемая основной кривой намагничивания. Изменение геометрических размеров, технологий изготовления деталей [5; 6], состава сплава окажет влияние на эту характеристику. Таким образом, основная кривая намагничивания деталей отражает их суммарные магнитные свойства, что позволяет рассматривать ее как характеристику элементов магнитной системы. Изменения свойств отдельных частей магнитопровода повлекут за собой и изменения рабочих характеристик электромагнитов – в том числе тяговых характеристик электромагнита.
Во время приемо-сдаточных испытаний производят измерения динамических тяговых характеристик. Эти характеристики связывают зависимость электромагнитной силы Fэ от изменяющейся в процессе работы величины зазора Fд = f(Δ) [7].
Для определения влияния магнитных характеристик каждой детали на общую тяговую характеристику электромагнита необходимо построить математическую регрессионную модель.
Цель исследования заключается в получении адекватной регрессионной математической модели, отражающей зависимость тяговой характеристики электромагнита с магнитными параметрами его составных частей. Такая регрессионная модель необходима для решения задачи комплементарной сборки, заключающейся во взаимодополняющем подборе деталей электромагнита по их магнитным свойствам, с целью уменьшить количество брака готовых изделий в процессе их производства [8].
Материалы и методы исследования
Для получения тяговых характеристик применено моделирование электромагнита в программном продукте COMSOL Multiphysics. Построена упрощенная модель на базе двухмерного осесимметричного представления (рис. 2).
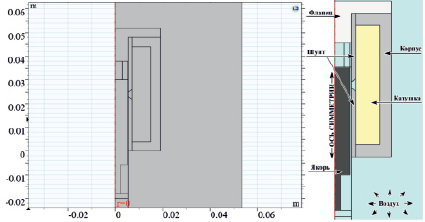
Рис. 2. Геометрическое представление модели (слева) и пояснение к геометрическому представлению (справа)
В модели рассматривалось влияние отклонения магнитной индукции насыщения материалов трех составляющих частей электромагнита (корпуса, магнитного шунта и якоря) на тяговую характеристику. Построенная модель имитирует работу электромагнита и позволяет получить зависимость между тяговым усилием и зазором в процессе движения якоря под действием электромагнитных сил.
Для проведения эксперимента использовалась методика планирования эксперимента [9]. Составлена матрица планирования, представленная в табл. 1, основанная на ортогональном центрально-композиционном плане (ОЦКП), включающем три фактора (отклонения максимальной индукции насыщения деталей электромагнита). План эксперимента содержит ядро, в виде полного факторного эксперимента, шесть звездных точек, расположенных симметрично относительно центра плана, и центр плана. Были проведены три повторения каждого эксперимента для расчета критерия адекватности полученной модели. В качестве отклика выбрана динамическая тяговая характеристика электромагнита, представленная в виде первой главной компоненты PC1 этой характеристики. Преобразование динамической характеристики в первую главную компоненту производилось по методике, описанной в [10; 11].
Главнокомпонентный анализ применен с целью сжатия информации и заключается в переходе в ортогональное пространство первой главной компоненты. Поскольку первая главная компонента имела дисперсию более 99,9 %, вторая главная компонента не учитывалась в эксперименте. Помимо этого, перевод динамической тяговой характеристики в пространство главных компонент позволяет избавиться от мультиколлинеарности тяговых характеристик и получить адекватную регрессионную модель.
Таким образом, эксперимент проводился с целью получения уравнения взаимосвязи между отклонениями индукции насыщения материалов деталей электромагнита и первой главной компонентой PC1, описывающей тяговую характеристику электромагнита. Результатом моделирования стало семейство графиков тяговых характеристик, изображенных на рис. 3.
Результаты исследования и их обсуждение
После проведенных модельных экспериментов данные обрабатывались в программном пакете Statistica. Результаты обработки представлены в табл. 2–4.
Получена адекватная модель с расчетным значением критерия Фишера, равным 0,318, при этом критическое значение критерия Фишера равно 3,68.
Таблица 1
Матрица ОЦКП
|
№ |
Bн якоря |
Bн шунта |
Bн корпуса |
PC 1 |
|||
|
Кодир. |
Физич. |
Кодир. |
Физич. |
Кодир. |
Физич. |
||
|
1 |
[+] |
+5 % |
[+] |
+5 % |
[+] |
+5 % |
-0.99996936161 |
|
2 |
[-] |
-5 % |
[+] |
+5 % |
[+] |
+5 % |
-0.99998092079 |
|
3 |
[+] |
+5 % |
[-] |
-5 % |
[+] |
+5 % |
-0.99999572771 |
|
4 |
[-] |
-5 % |
[-] |
-5 % |
[+] |
+5 % |
-0.99999210790 |
|
5 |
[+] |
+5 % |
[+] |
+5 % |
[-] |
-5 % |
-0.99999445573 |
|
6 |
[-] |
-5 % |
[+] |
+5 % |
[-] |
-5 % |
-0.99999758042 |
|
7 |
[+] |
+5 % |
[-] |
-5 % |
[-] |
-5 % |
-0.99998533392 |
|
8 |
[-] |
-5 % |
[-] |
-5 % |
[-] |
-5 % |
-0.99997114667 |
|
9 |
[-α] |
-6,075 % |
[0] |
0 % |
[0] |
0 % |
-0.99999776751 |
|
10 |
[+α] |
+6,075 % |
[0] |
0 % |
[0] |
0 % |
-0.99999841505 |
|
11 |
[0] |
0 % |
[-α] |
-6,075 % |
[0] |
0 % |
-0.99998467421 |
|
12 |
[0] |
0 % |
[+α] |
+6,075 % |
[0] |
0 % |
-0.99998188734 |
|
13 |
[0] |
0 % |
[0] |
0 % |
[-α] |
-6,075 % |
-0.99999428441 |
|
14 |
[0] |
0 % |
[0] |
0 % |
[+α] |
+6,075 % |
-0.99999044295 |
|
15 |
[0] |
0 % |
[0] |
0 % |
[0] |
0 % |
-0.99999973724 |
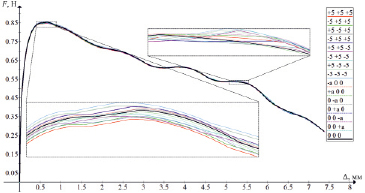
Рис. 3. Семейство тяговых характеристик электромагнита, полученных из модели
Таблица 2
Листинг с оценкой коэффициентов регрессии в кодированных значениях
|
Фактор |
Эффект |
Сред. квад. откл. |
t(30) |
p |
-95 % Довер. инт. |
+95 % Довер. инт. |
Коэф. |
|
Средн./Свобод. член |
-0,999998 |
0,000002 |
-658131 |
0,000 |
-1,0 |
-0,99 |
-0,999998 |
|
(1L)Bн якоря |
-0,000001 |
0,000001 |
-1 |
0,613 |
-0,0 |
0,00 |
-0,000000 |
|
(1Q)Bн якоря |
-0,000001 |
0,000002 |
-0 |
0,628 |
-0,0 |
0,00 |
-0,000001 |
|
(2L)Bн шунта |
0,000001 |
0,000001 |
1 |
0,487 |
-0,0 |
0,00 |
0,000000 |
|
(2Q)Bн шунта |
0,000019 |
0,000002 |
9 |
0,000 |
0,0 |
0,00 |
0,000009 |
|
(3L)Bн корпуса |
0,000003 |
0,000001 |
2 |
0,058 |
-0,0 |
0,00 |
0,000001 |
|
(3Q)Bн корпуса |
0,000007 |
0,000002 |
3 |
0,005 |
0,0 |
0,00 |
0,000003 |
|
1L и 2L |
0,000008 |
0,000002 |
5 |
0,000 |
0,0 |
0,00 |
0,000004 |
|
1L и 3L |
0,000005 |
0,000002 |
3 |
0,007 |
0,0 |
0,00 |
0,000002 |
|
2L и 3L |
0,000018 |
0,000002 |
11 |
0,000 |
0,0 |
0,00 |
0,000009 |
Таблица 3
Листинг с оценкой коэффициентов регрессии в физических значениях
|
Фактор |
Коэф. регр. |
Сред. квад. откл. |
t(30) |
p |
-95 % Довер. инт. |
+95 % Довер. инт. |
|
Средн./Свобод. член |
-0,999998 |
0,000002 |
-658 |
0,000 |
0 |
-1,00000 |
|
(1L)Bн якоря |
-0,000007 |
0,000014 |
-1 |
0,613 |
-0,000 |
0,000 |
|
(1Q)Bн якоря |
-0,000216 |
0,000442 |
-0 |
0,628 |
-0,001 |
-0,001 |
|
(2L)Bн шунта |
0,000010 |
0,000014 |
1 |
0,487 |
-0,000 |
-0,000 |
|
(2Q)Bн шунта |
0,003797 |
0,000442 |
9 |
0,000 |
0,003 |
0,003 |
|
(3L)Bн корпуса |
0,000028 |
0,000014 |
2 |
0,058 |
-0,000 |
-0,000 |
|
(3Q)Bн корпуса |
0,001336 |
0,000442 |
3 |
0,005 |
0,000 |
0,000 |
|
1L и 2L |
0,001625 |
0,000327 |
5 |
0,000 |
0,001 |
0,001 |
|
1L и 3L |
0,000950 |
0,000327 |
3 |
0,007 |
0,000 |
0,000 |
|
2L и 3L |
0,003655 |
0,000327 |
11 |
0,000 |
0,003 |
0,003 |
Таблица 4
Листинг с оценкой адекватности модели
|
Фактор |
Сумм. сред. квадр. ошиб. |
Степ. своб. |
Дисперсия |
F (крит. Фишера) |
p |
|
(1L)Bн якоря |
4,19E-12 |
1 |
4,19E-12 |
0,262 |
0,613 |
|
(1Q)Bн якоря |
3,83E-12 |
1 |
3,83E-12 |
0,239 |
0,628 |
|
(2L)Bн шунта |
7,94E-12 |
1 |
7,94E-12 |
0,496 |
0,487 |
|
(2Q)Bн шунта |
1,18E-09 |
1 |
1,18E-09 |
73,68 |
0,000 |
|
(3L)Bн корпуса |
6,22E-11 |
1 |
6,22E-11 |
3,886 |
0,058 |
|
(3Q)Bн корпуса |
1,46E-10 |
1 |
1,46E-10 |
9,118 |
0,005 |
|
1L и 2L |
3,96E-10 |
1 |
3,96E-10 |
24,74 |
0,000 |
|
1L и 3L |
1,35E-10 |
1 |
1,35E-10 |
8,463 |
0,007 |
|
2L и 3L |
2,00E-09 |
1 |
2,00E-09 |
125,3 |
0,000 |
|
Отсут. соглас. |
2,54E-11 |
5 |
5,09E-12 |
0,318 |
0,898 |
|
Чистая ошибка |
4,80E-10 |
30 |
1,60E-11 |
||
|
Суммар. ошиб. сред. кв. откл. |
4,44E-09 |
44 |
Полученное уравнение регрессии, отражающее зависимость первой главной компоненты и отклонений максимальных индукций материалов магнитного шунта δBш, корпуса δBк и якоря δBяк, имеет вид:
PC1 = –1 + 3,80?10-3?δBш2 + 1,34?10-3?δBк2 +
+ 1,63?10-3?δBяк?δBш + 0,95?10-3?δBяк?δBк +
+ 3,66?10-3?δBк?δBш.
Данные уравнения регрессии можно использовать при подборе деталей электромагнита на комплементарной, взаимодополняющей основе, заключающейся в выборе таких деталей для сборки, чтобы в собранном виде их магнитные свойства обеспечивали наименьшее отклонение тяговой характеристики электромагнита.
Выводы
1. Результатом проведенного эксперимента стала регрессионная математическая модель, позволяющая осуществлять комплементарный подбор деталей электромагнита по их отклонениям магнитной индукции насыщения.
2. Из полученной модели видно, что наибольшую зависимость на тяговую характеристику оказывают магнитные свойства материала магнитного шунта и их взаимодействие с магнитными свойствами материала корпуса, при этом магнитные свойства якоря слабо влияют на параметры тяговой характеристики, их влияние проявляется только во взаимодействии с магнитными свойствами материалов шунта и корпуса.
3. Полученная модель позволит реализовать метод комплементарной сборки, заключающийся в подборе комплекта деталей для сборки электромагнита таким образом, чтобы отклонение от номинальных характеристик одних компонентов компенсировало отклонение других с целью получить требуемую тяговую характеристику.
Библиографическая ссылка
Гладких С.А., Ланкин А.М., Ланкин М.В., Ткаченко Г.И. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ ЗАВИСИМОСТИ ТЯГОВЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАГНИТОВ ОТ МАГНИТНЫХ ХАРАКТЕРИСТИК ИХ СОСТАВНЫХ ЧАСТЕЙ // Современные наукоемкие технологии. 2020. № 8. С. 32-37;URL: https://top-technologies.ru/ru/article/view?id=38169 (дата обращения: 16.02.2026).
DOI: https://doi.org/10.17513/snt.38169



