Анализ предметной области в сфере управления испытаниями высокотехнологичных капиталоемких комплексов различного назначения показывает [1; 2], что ранее не рассматривались вопросы последовательной оптимизации процесса отработки новых образцов по критерию минимизации риска нарушения сроков, установленных заказчиком, или по критерию минимизации риска перерасхода выделенных на испытания средств.
При разработке современных распределенных измерительных систем, включающих наземные средства и аппаратуру на борту подвижных объектов (ПО), необходимо учитывать ряд факторов, усложняющих испытания. Первый фактор – это ограниченный энергетический ресурс, на восполнение которого (и, соответственно, на возобновление испытаний) требуется определенное время. Второй фактор – зависимость графика испытаний от закономерностей вхождения наблюдаемых объектов в зоны оптической досягаемости каждого комплекса. Третий фактор – некоторая недостоверность прогноза о возможном наступлении негативных воздействий среды на процедуру измерений, вследствие чего необходимо своевременно перепланировать распределение задействуемого в испытаниях кластера ПО между комплексами, не попадающими в неблагоприятные условия. Возникает задача организации адаптивного управления процессом измерений, процессом прогнозирования и процессом «подключения» к испытаниям (включая перебазирование) дополнительных наземных оптических измерительных комплексов (НОИК).
Исторический анализ хода реализации ресурсозатратных программ создания новых, наукоемких технических комплексов показывает, что при администрировании всех стадий жизненного цикла необходимо учитывать и минимизировать риски различного происхождения. Рассмотрим задачу минимизации риска RТпл невыполнения в заданный заказчиком срок Тпл программы испытаний нового измерительного комплекса. Программы испытаний сложных технических систем, как правило, предусматривают реализацию последовательных этапов; при выполнении работ на каком-либо этапе (кроме последнего) с некоторым отставанием для минимизации риска RТпл необходимо задействование дополнительных средств (и соответствующее финансовое обеспечение) с целью предотвращения потенциального опоздания. В литературе по планированию эксперимента [1–3] подробно изложены как общенаучные методы проведения физико-химических экспериментов, так и их прикладные аспекты. В работах [4–6] детально описаны задачи оптимизации режимов радиолокационных измерений, однако не учтена специфика функционирования оптических средств при управлении движением ПО различных типов. Первая особенность заключается в необходимости учета стохастического характера негативного воздействия атмосферных явлений на работу аппаратуры [7; 8]. Вторая особенность связана с технологией применения ПО, параметры движения которых подлежат измерениям.
Таким образом, критериями формализации задачи оптимального управления процессом испытаний являются:
1) минимизация риска срыва выполнения программы испытаний в заданный заказчиком срок;
2) минимизация величины дополнительных ресурсов, привлекаемых для обеспечения своевременного завершения испытаний.
Возможны два подхода к решению данной задачи: вероятностно-событийный и вероятностно-интервальный.
Вероятностно-событийный метод исследования и результаты его реализации
Центральной задачей при проведении испытаний нового измерительного комплекса является проведение заданного (рассчитанного по специальным методикам) числа измерений в ходе реализации каждого этапа программы. Если первый этап не закончился успешным выполнением частного плана, то для проведения дополнительной серии измерений необходимо некоторое время. Закон распределения этого «добавочного интервала» может быть найден посредством анализа характеристик движения объекта измерений.
Рассмотрим процесс испытаний комплексов, размещенных в определенном порядке на поверхности Земли и взаимодействующих с бортовой аппаратурой ПО. Баллистические расчеты показывают [4; 6; 7], что каждому заданному моменту tн начала испытаний соответствует конкретная комбинация распределения интервалов технологически возможной работы оптических средств.
В табл. 1 представлена динамика распределения наблюдаемости при смещении момента начала испытаний (измерений); пример соответствует условному трехсуточному интервалу. Для орбит ПО с повторяющейся трассой комбинация распределения будет повторяться через соответствующее число суток (витков), но необходимо заметить, что изменение модели движения приводит к существенным отклонениям прогнозного движения от эталонного. Так, повышение степени учета порядка зональных и тессеральных гармоник гравитационного поля до «4х4» приводит к увеличению максимального отклонения от эталонного движения до 140 км в трансверсальном направлении.
В табл. 1 использованы следующие обозначения: Тпр – плановая продолжительность наблюдений, δ – параметр дискретности поступления команд на начало серии наблюдений, N – число возможных сеансов, N = Тпр / δ.
Следует отметить, что большое количество нулевых значений величины ?tзн означает, что вероятность выполнения программы испытаний в заданный срок весьма мала. Представленное распределение зон существенно зависит от величины δ, но инвариантно по отношению к используемым системам отсчета, хотя координация планов в практике управления многими типами ПО не автоматизирована по всем приложениям и имеет подборочный характер [6]. Следует отметить также, что задействование дополнительных средств не всегда возможно «физически»: баллистические расчеты могут показать неприемлемое время для формирования новой последовательности. Динамика распределения зон наблюдения представлена в табл. 1.
Таблица 1
Динамика распределения зон наблюдения
|
t, мин |
tн |
tн + δ |
.… |
tн + 8 δ |
tн + 9 δ |
… |
tн + 17 δ |
tн + 18 δ |
|
?tзн, мин |
7 |
7 – δ |
… |
3 |
0 |
… |
7 |
7 – δ |
|
t, мин |
tн + 19 δ |
tн + 20 δ |
… |
tн + 28 δ |
tн + 29 δ |
… |
N-1 |
Тпр |
|
?tзн, мин |
5 |
5 – δ |
… |
3 |
0 |
… |
7 |
7 – δ |
Данные табл. 1, в свою очередь, позволяют табулировать зависимость ?tзн = ϑ(tн) на весь программный период (либо представить графически как немонотонную функцию с разрывами).
Для определения функции распределения продолжительности испытаний рассмотрим в качестве примера вариант с ограничением по энергетике N ≤ 3 (не более 3 попыток); конкретный момент tн считаем заданным.
Обозначим: ?τi – величина опоздания, P1 – вероятность технического отказа, P2 – вероятность срыва сеанса измерений вследствие недостоверного геофизического прогноза. Ряд распределения продолжительности дополнительных временных интервалов (значений «опозданий»), полученный для круговой орбиты с высотой 600 км при P1 = 0.9, P2 = 0.8, представлен в табл. 2.
Таблица 2
Ряд распределения случайной величины ?τi
|
τ, час |
0 |
1.617 |
3.05 |
|
P(?τi = τ) |
0.720 |
0.216 |
0.0783 |
Вследствие наличия разрывов в графике временной функции – зависимости от tн совокупности моментов возможного проведения измерений – вероятность своевременного завершения программы может быть вычислена только численно (даже без учета влияния геофизических факторов; небольшое упрощение расчетов дает рассмотрение изомаршрутных систем периодического обзора).
Контроль правильности расчетов величин P(?τi = τ) должен быть проведен методом «геометрических вероятностей» [9] для заданных координат местоположения измерительного комплекса (геоцентрической широты YП и долготы lП).
Но так как фактическое распределение интервалов наблюдаемости ПО зависит от момента принятия решения о начале измерений (в более узкой трактовке – от величины tн), то вероятность реализации возможного значения опоздания Pоп является функцией случайного аргумента tн.
Следовательно, возникает новая (дополнительная) задача по вычислению функции распределения оцениваемой вероятности как непрерывной случайной величины (СВ). Для этого первоначально рассчитывается и аппроксимируется немонотонная негладкая функциональная зависимость Pоп = φ(tн). Далее для нахождения функции распределения G(Pi) величины Pоп выделяются те участки ?i(Y) кривой Pоп = φ(x), на которых выполняется условие Pоп < Y. Для расчета значений функции распределения величины Pоп = φ(tн) используется выражение
G(Pоп) = 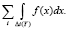
Границы интервалов ?i(Y) зависят от Y, но не могут быть выражены как явные функции и определяются из соответствующих транспонированных таблиц, вычисляемых по конкретным исходным данным.
Из вышеизложенного следует, что критерий оптимизации управления ходом испытаний должен включать показатель из класса «гарантирующее оценочное высказывание»: вероятность Q обеспечения выполнения неравенства RТпл ≤ Rпр. Вероятность Q рассчитывается через обратную функцию распределения величины ?τ; степень гарантии Rпр устанавливается заказчиком, исходя из приемлемого уровня точности расчета величины Q.
Показатель Q = P(RТпл ≤ Rпр) подлежит максимизации, при решении обратной задачи (задачи синтеза системы) на основе Q могут быть сформулированы требования к атрибутам системы геофизического обеспечения.
Вероятностно-интервальный метод исследования и результаты его реализации
При проведении анализа ресурсозатратных аспектов необходимо предусмотреть, что на концептуальной фазе разработки программы целесообразно [2; 3] учесть влияние случайных факторов, вызывающих расчетные временные отклонения – и некоторые опережения, и несущественные отставания – в штатных ситуациях (инерционность оборудования, неизбежные конфликты IР-адресов, человеческий фактор и др.).
Значит, продолжительности ti этапов должны рассматриваться как СВ, математические ожидания которых равны плановым значениям ti, а среднеквадратические отклонения составляют незначительную долю от математических ожиданий. Поэтому априорная вероятность Pпл = P(Т ≤ Тпл) выполнения программы испытаний в заданный заказчиком срок всегда близка к единице.
Рассмотрим пример анализа четырехэтапной программы с параметрами (в часах): t1 = 10, t2 = 13, t3 = 12, t4 = 10, σ1 = σ2 = σ3 = σ4 = 0,75; Тпл = 47. После проведения расчетов получаем, что при опоздании с завершением только первого этапа на 10 % вероятность своевременного выполнения программы уменьшается с 0.9 до 0.75; при задержке на 20 % – до 0.5; при опоздании на 30 % вероятность выполнения программы испытаний в заданный заказчиком срок становится равной нулю.
Если программа испытаний включает 2–3 этапа, то задача минимизации расхода дополнительно привлекаемых средств с ограничением Pпл. ≥ Pтр может быть сформулирована как задача нелинейного программирования. Следует заметить, что при проведении испытаний с использованием на одном временном интервале нескольких НОИК алгоритм решения оптимизационной задачи должен быть дополнен блоком рационального выбора приемлемой комбинации распределения. Вычислительные трудности здесь отсутствуют, хотя имеет место резкое увеличение размерности исходной вероятностной матрицы. Приведем пример расширения матрицы для варианта планирования «по одному сеансу на 2 суток вперед»: 1*1 + 2*2 + 1*1 + 2*2 (схема № 1), 1*1 + 2*2 + 2*1 + 1*2 (схема № 2), 1*2 + + 2*1 + 1*1 + 2*2 (схема № 3), 1*2 + + 2*1 + 1*2 + 2*1 (схема № 4). Следует отметить также, что для определенного класса ПО моменты их входа в зоны наблюдаемости не повторяются и возможны дальнейшее наращивание «цепочки» и рандомизация последовательностей сеансов измерений.
При числе этапов N ≥ 4 резко возрастает размерность ветвящегося процесса вследствие увеличения числа логических последовательностей вариантов доработок и их глубины, поэтому «строгая» аналитическая формализация задачи затруднительна. Но современные технологии анализа информации в программно-цифровой среде big data (платформенные сервисы, создаваемые для расчетов на ЭВМ петафлопсного диапазона, а в дальнейшем – на квантовых компьютерах мощностью в несколько кубитов) позволяют [10–12] реализовать двухконтурную вычислительную схему – накапливание и «табулирование» информации по различным процедурам доработки испытываемого комплекса, ее хранение для каждого предыдущего шага и использование при обратном проходе для выбора оптимального градиента.
Логика алгоритма заключается в адекватном реагировании на результаты каждого этапа и формировании массива ситуационных решений, соответствующих обстановке. На каждом шаге алгоритма осуществляется отыскание корней трансцендентного уравнения
θυ-1(yυ-1, λυ-1, …, λN, Тпл, t1*, … t**υ-1) + RТпл = 1,
где yυ-1 – параметр корректировки;
λυ-1 – параметр закона распределения величины tυ-1;
t*υ-1 – фактический (заранее неизвестный) срок завершения этапа.
Например, для однопараметрического закона распределения, соответствующего второму этапу, уравнение реконфигурации имеет вид
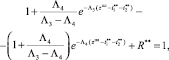
где R** – значение обратной функции распределения, прогнозируемое по результатам второго этапа.
Для двухпараметрического закона распределения величины ti трансцендентное уравнение реконфигурации, соответствующее третьему этапу, имеет вид
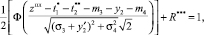
где R*** – значения риска RТпл, прогнозируемые по результатам третьего этапа.
Для реализации разработанного алгоритма необходимы предварительные исследования по нахождению связи между характеристиками каждого нового варианта доработки программы, расходом обеспечивающих ресурсов по предлагаемому варианту (например, подключение и прием информации от резервных комплексов; перезагрузка подсистемы информационного обеспечения, оперативный реинжиниринг структуры участвующих организаций) и компенсируемым «размером опоздания».
Предлагаемый подход учитывает классические требования теории планирования эксперимента – обязательность рандомизации и обеспечение возможности корректировки программы – и может быть отнесен к группе методов проактивного управления [13–15].
Заключение
В статье предложены два подхода к оптимизации программы испытаний наземных оптических измерительных комплексов. Гарантированная вероятность реализации программы испытаний в плановый срок определяется с использованием аппарата теории функций случайного аргумента, а также методом «геометрических вероятностей».
Минимизация расхода средств, дополнительно привлекаемых для ликвидации риска срыва программы испытаний, основана на реализации двухконтурной вычислительной схемы. Разработанные методики соответствуют требованиям адаптивности и рандомизации, протестированы на примерах и могут быть использованы как на стадии концептуальной проработки программ испытаний распределенных измерительных систем, так и в ходе оперативного контроля расхода средств на стадии реальных испытаний. Включение предложенных алгоритмов в состав методики учета вероятностно-временных характеристик системы информационного обеспечения позволит повысить эффективность функционирования НОИК за счет реализации принципа проактивного управления.
Библиографическая ссылка
Волков В.Ф., Пономарев А.С. АЛГОРИТМЫ ОПТИМИЗАЦИИ ПРОГРАММЫ ИСПЫТАНИЙ НАЗЕМНЫХ ОПТИЧЕСКИХ ИЗМЕРИТЕЛЬНЫХ КОМПЛЕКСОВ // Современные наукоемкие технологии. 2020. № 8. С. 15-19;URL: https://top-technologies.ru/ru/article/view?id=38166 (дата обращения: 28.12.2025).
DOI: https://doi.org/10.17513/snt.38166



