Высокий профессионализм учителя помогает результативно организовывать процесс обучения, развивая интерес и мотивацию учащихся к учебной деятельности, стремление к совершенствованию знаний и умений. Уровень знаний и умений обучающихся и уровень профессионализма учителя, определяемый профессиональной компетентностью, считаются наиболее характерными показателями качества образования.
Профессиональный рост учителя – это непрерывный процесс раскрытия личностно-профессионального потенциала учителя, влияющего на качество педагогической деятельности. Огромную роль в становлении и росте профессионализма педагога играет заинтересованность педагога в самосовершенствовании: обмен опытом, посещение уроков учителей-мастеров, общение с методистами, участие в конференциях, семинарах, а также в конкурсах профессионального мастерства и олимпиадах для учителей.
В настоящее время проводятся различные виды олимпиад для студентов педагогического образования и учителей. Здесь можно выделить две разновидности олимпиад: платные олимпиады для учителей (так же, как и для студентов), а также метапредметные олимпиады для учителей, которые не столь давно начали проводиться в различных регионах нашей страны.
В сети Интернет существует огромное количество различных сайтов, которые предлагают следующее: поучаствовать в блиц-олимпиаде по своему предмету или по методике преподавания и буквально через 10 минут получить именной диплом или сертификат, подтверждающий ваше участие. К сожалению, подобные олимпиады не имеют никакой юридической силы.
Второй вариант олимпиад для педагогов кажется нам наиболее приемлемым, но он, к сожалению, пока недостаточно широко распространен – это метапредметные олимпиады для учителей. В качестве примера можно привести метапредметную олимпиаду «Московский учитель», которая проводится с 2014 г. [1]. Другой интересный пример – олимпиада для учителей математики, которую проводит Новосибирский институт повышения квалификации и переподготовки работников образования «Учитель математики – Профессионал». Основной задачей олимпиады является улучшение качества образовательных услуг по повышению квалификации и методическому обеспечению профессионального развития работников образования Новосибирской области [2].
Резюмируя все вышесказанное, можно считать олимпиады и конкурсы для учителей не только формой их самообразования и самосовершенствования, но и способом формирования профессиональной компетентности будущего учителя.
Материалы и методы исследования
Материалом исследования стала научная, научно-методическая литература. Среди исследуемых проблем особого внимания заслуживает проблема формирования профессиональной компетентности будущих учителей математики. В настоящее время многие исследователи неоднозначно определяют понятие профессиональной компетентности. Так, например, А.В. Хуторской вводит данное понятие как «совокупность взаимосвязанных качеств личности (знаний, умений, навыков, способов деятельности), задаваемых по отношению к определенному кругу вопросов и необходимых, чтобы качественно продуктивно действовать по отношению к ним», Э.Ф. Зеер, О.Н. Шахматова и др. – «совокупность профессиональных знаний, умений, способов выполнения профессиональной деятельности» [3].
В отечественной психолого-педагогической литературе наиболее распространенным является следующее: «профессиональная компетентность – это качество, свойство или состояние специалиста, обеспечивающее вместе или в отдельности его физическое, психическое и духовное соответствие необходимости, потребности, требованиям определенной профессии, специальности, специализации, стандартам квалификации, занимаемой или исполняемой служебной должности» [4].
В своей работе Т.С. Мамонтова вводит понятие профессионально-методической компетентности будущего учителя математики как «владение совокупностью профессионально-методических компетенций, означающее его готовность к осознанному и качественному выполнению профессионально-методической деятельности» [5].
В качестве методов использовались теоретический анализ научно-методической литературы, систематизация и обобщение собственного педагогического опыта.
Результаты исследования и их обсуждение
Как одна из эффективных форм развития профессиональной компетентности, олимпиада имеет большое значение в профессиональной подготовке студентов – будущих учителей, дает возможность применять полученные и усвоенные знания, способствует совершенствованию владения педагогическими методиками. Предметные и педагогические олимпиады, проводимые в вузах, обычно содержат теоретические и творческие задания, которые характеризуют общепрофессиональные компетенции. Для профессионального формирования будущего учителя математики наряду с общепрофессиональными компетенциями необходимо сформировать методические умения, как показатели сформированности профессиональных компетенций. Отсюда необходимым является расширение видов организуемых в вузах олимпиад и включение в практику методических олимпиад [6].
В связи с этим кафедрой методики преподавания математики Северо-Восточного федерального университета была проявлена инициатива проведения методической олимпиады для будущих и практикующих учителей математики в Республике Саха (Якутия). Целью данной олимпиады стало проведение независимой экспертизы сформированности профессиональной компетенции студентов и повышения качества образования посредством стимулирования их познавательной активности и раскрытия творческого потенциала, а также для выявления, поощрения и поддержки учителей математики, обладающих высокими методическими и предметными знаниями и профессиональными компетенциями, необходимыми для достижения высоких образовательных результатов учащихся.
В пособии «Методика обучения математике в условиях реализации компетентностной образовательной парадигмы» отражены вопросы формирования профессионально-методической компетентности учителя математики посредством данной методической олимпиады, традиционно проводимой кафедрой методики преподавания математики. Отмечено, что использование на практических занятиях заданий, предложенных на методических олимпиадах, оказывает влияние на формирование у студентов творческих умений и навыков при их решении и достаточно высокую степень математической и методической культуры при их выполнении [7].
Олимпиада проводится с 2010 г. ежегодно в рамках научно-практической конференции учителей-исследователей, посвященной памяти Народного учителя СССР Михаила Андреевича Алексеева. Пилотный проект этой олимпиады проведен в 2009 г. только для студентов – будущих учителей математики. Положительные результаты проведения этой олимпиады натолкнули на идею проведения такой методической олимпиады и среди учителей математики, которая в дальнейшем превратилась в традиционную. Результаты олимпиады подводятся отдельно для студентов и учителей.
Каждый год кафедра старается приурочить Олимпиаду к знаменательным датам, связанным с математическим образованием или памятью одного из ведущих математиков, специалистов по методике преподавания республики.
Первая совместная методическая олимпиада студентов и учителей математики Республики Саха (Якутия) – 2010 была посвящена памяти И.Г. Дмитриева. Дмитриев Иван Григорьевич, кандидат физико-математических наук, почетный работник высшего профессионального образования РФ, отличник образования РС(Я), обладатель знака «Учитель учителей» РС(Я), лауреат Государственной премии РС(Я) в области педагогики имени народного учителя СССР М.А. Алексеева и премии «Знанием победишь» I Президента РС(Я).
Методическая олимпиада студентов и учителей математики РС(Я) 2011 г. была посвящена памяти Афанасия Егоровича Алексеева, первого в Якутском государственном университете ведущего специалиста по методике преподавания математики, III – памяти Иннокентия Герасимовича Егорова, первого декана математического факультета ЯГУ, IV и IX – памяти Петровой Антонины Ивановны д.п.н., профессора кафедры методики преподавания математики, одного из инициаторов методической олимпиады, V олимпиада – 25-летнему юбилею кафедры методики преподавания математики СВФУ имени М.К. Аммосова, VI – 80-летию физико-математического образования в РС(Я), VII – 85-летию со дня рождения Алиева Исмаил Шахбаз-оглы, к.ф.-м.н., первого директора Республиканской физико-математической школы при Якутском госуниверситете, VIII олимпиада 2017 г. приурочена к 100-летию со дня рождения Народного учителя СССР Михаила Андреевича Алексеева.
X юбилейная методическая олимпиада студентов и учителей математики Республики Саха (Якутия) на Кубок заведующего кафедрой методики преподавания математики была посвящена 30-летию образования кафедры методики преподавания математики СВФУ имени М.К. Аммосова. Приведем задания X юбилейной методической олимпиады студентов и учителей, проведенной в 2019 г.
I. Ответьте на вопросы:
I.1. (Предложила В.Н. Эверстова) Проиллюстрируйте аналитический и синтетический методы доказательства неравенства:
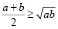, где a ≥ 0, b ≥ 0.
I.2. (Предложила Н.В. Аргунова) Эта система включает 5 компонентов, которые могут быть взаимосвязаны по схеме А.М. Пышкало, а могут быть и иерархично связаны по схеме А.А. Кузнецова. Дайте полное название этой системы и ее компонентов.
I.3. (Предложила М.И. Баишева) Гармонический ряд – сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда
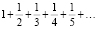
(Ряд назван гармоническим, так как складывается из «гармоник»: k-я гармоника, извлекаемая из скрипичной струны, – это основной тон, производимый струной длиной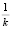 
от длины исходной струны). Приведите алгебраическое объяснение названия такого ряда гармоническим. Приведите пример объяснения.
II. Перед Вами тексты, которые могут содержать математические ошибки. Ошибки могут быть как в формулировках утверждений, так и в их доказательствах (решениях). В случае, если доказываемое утверждение верно, укажите ошибки в доказательстве (решении). Если утверждение неверно, объясните, почему это так, и найдите ошибку в приведенном доказательстве (решении).
II.1. (Предложила А.М. Попова) Вычислить
arcctg(tg10) – arccos(sin10).
«Решение. По свойству обратных тригонометрических функций
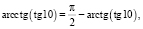
для tg 10 ∈(–∞; ∞),
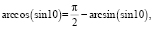
для sin 10 ∈(–1; 1).
Тогда
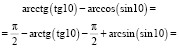
= –10 + 10 = 0.
Ответ: 0».
II.2. (Предложила Н.В. Аргунова) При каких значениях k прямая y = kx имеет с графиком функции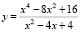 
ровно одну общую точку?
«Решение. Преобразовываем выражение
.
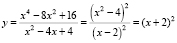Составим уравнение касательной к графику функции y = (x + 2)2 в некоторой точке x0. Это уравнение имеет вид
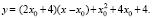
Подставив в него (0; 0), получим, что x0 = 2. Тогда y = 0 и y = 8x.
Ответ: 0; 8».
II.3. (Предложил А.Н. Павлов) ABCDA1B1C1D1 – прямоугольный параллелепипед, O – его центр. Докажите, что проекции точек O и A на плоскость A1BD (точки P и H соответственно), а также точка M (пересечения плоскости A1BD и диагонали AC1) являются соответственно центром описанной окружности, ортоцентром и точкой пересечения медиан треугольника A1BD.
«Решение. Точки A, O и M лежат на диагонали AC1 параллелепипеда. Через эту прямую и точку P проходит плоскость (скажем, α), притом только одна. С другой стороны, прямые OP и AH параллельны как перпендикуляры к одной и той же плоскости, значит, лежат на одной плоскости. И эта плоскость есть плоскость α. Плоскости α и A1BD пересекаются по прямой. Точки H, P и M лежат на обеих плоскостях, значит, на одной прямой – прямой пересечения плоскостей.
Отрезки OA1, OB и OD равны, так как являются радиусами сферы, описанной вокруг параллелепипеда. Тогда равны и их проекции PA1, PB и PD на плоскость A1BD. Тогда P – центр описанной окружности треугольника A1BD.
Прямая AH перпендикулярна A1H (по определению прямой, перпендикулярной плоскости). Опустим перпендикуляр HA0 из точки H на отрезок BD. Так как прямая HA0 также перпендикулярна к AH и лежит на одной плоскости с прямой A1H, то эти прямые совпадают. То есть A1A0 – высота треугольника A1BD. Аналогично доказываем, что и другие высоты также проходят через точку H.
Плоскости A1BD и AA1C1C пересекаются по прямой A1A2, где A2 – середина отрезка BD. Значит, отрезок A1A2 – медиана треугольника A1BD. Аналогично, плоскости A1BD и ADC1B1 пересекаются по прямой DD2, где D2 – середина отрезка A1B. Значит, отрезок DD2 – медиана треугольника A1BD. Значит, M – точка пересечения медиан треугольника A1BD. Что требовалось доказать».
III. Решите задачи.
III.1. (Предложил А.В. Софронов) Разрежьте квадрат 7×7 по линиям клеток на возможно большее число различных прямоугольников. Найдите все возможные разные способы (способы считаются различными, если у них разные наборы прямоугольников; способы с одинаковыми наборами считаются равными вне зависимости от расположения прямоугольников).
III.2. (Предложила Н.В. Аргунова) Докажите, что
sin10 + sin20 > sin30.
III.3. (Предложил Г.К. Муравин) Докажите, что периметр треугольника ABC больше периметра ANC, если точка N расположена внутри треугольника ABC.
IV. Найдите как можно больше способов решения задачи и запишите эти решения так, как Вы бы хотели их видеть в работе Вашего ученика. (Различными считаются способы, использующие различные математические идеи, а также различные технические приемы реализации одной и той же идеи.)
(Предложил В.П. Ефремов) Биссектриса BD внутреннего угла треугольника ABC делит противоположную сторону на отрезки, пропорциональные сторонам BC и BA треугольника.
За 10 лет проведения олимпиады в ней приняли участие более 500 студентов и более 500 учителей математики Республики Саха (Якутия).
Заключение
Опыт проведения методической олимпиады показал, что предлагаемые в ней задания способствуют формированию профессиональной компетентности учителя математики посредством осознания положительного опыта сочетания исторических традиций с современными направлениями методики обучения математики, осмысления инновационных идей и оценивают методические умения студентов педагогического образования и учителей математики. Такую олимпиаду можно считать средством профессионального развития педагога, ведь она позволяет учителю самосовершенствоваться и получить новый импульс для дальнейшего творчества.
Следует также отметить, что, по мнению участников и организаторов, методическая олимпиада способствует взаимодействию преподавателей вуза, учителей математики общеобразовательных школ и студентов – будущих учителей математики, дает им возможность учиться друг у друга и совместно решать педагогические проблемы методического характера.
Библиографическая ссылка
Аргунова Н.В., Макарова С.М., Попова А.М. МЕТОДИЧЕСКАЯ ОЛИМПИАДА УЧИТЕЛЕЙ МАТЕМАТИКИ И СТУДЕНТОВ ПЕДАГОГИЧЕСКОГО ОТДЕЛЕНИЯ (ОПЫТ РЕСПУБЛИКИ САХА (ЯКУТИЯ)) // Современные наукоемкие технологии. – 2020. – № 7. – С. 116-120;URL: https://top-technologies.ru/ru/article/view?id=38144 (дата обращения: 16.04.2024).